1109145233

17

Zadanie 3:

Dla manipulatora przestrzennego typu 3R (rys.4) należy: związać z każdym członem układ współrzędnych i przedstawić na rysunku. Podać w tabeli parametry D-H i obliczyć macierze jednorodne '^-IT, a następnie rozwiązać proste zadanie kinematyki dla tego manipulatora i obliczyć położenie i orientację układu {4} w układzie bazowym.

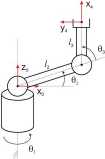
Rys. 4: Manipulator przestrzenny 3R

18

Rozwiązanie:

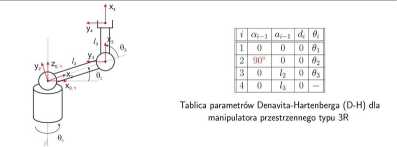
Korzystając z wzoru na macierz przejścia j *T obliczamy

Cl	-Si	0 0		^c2	-S2	0	dl		C3	—83	0 k		1 0 0	k
Si	Cl	0 0	\t =	0	0	-1	0	l T =	S3	C3	0 0	^3ĄT =	0 1 0	0
0	0	1 0		S2	C2	0	0		0	0	1 0		0 0 1	0
0	0	0 1		0	0	0	1		0	0	0 1		0 0 0	1

Rozwiązaniem prostego zadania kinematyki jest macierz