6355786271

EKONOMI fi MENEDŻERSKA

Wykład 1 Wprowadzenie do ekonomii menedżerskiej 6

Przyrównanie cząstkowych pochodnych do zera:

!

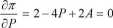
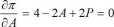
pozwala wyznaczyć optymalne decyzje w zakresie ceny produktu i wydatków na reklamę:    P* =3, A* = 5.

Przykład II producent, który ma ograniczone zdolności produkcyjne i sprzedaje swoje wyroby na dwóch (lub więcej) rynkach

lub producent, który ma ograniczone zdolności produkcyjne i produkuje dwa produkty (lub więcej):

Dane:

Funkcja zysku:

^K (Q\ > Ql) - (2001 - O,501² ) + (4002    ^max

Ograniczenie: 0i + 02 * 25

Metoda rozwiązania: - metoda mnożników Lagrange’a Funkcja Lagrange’a:

ra = *• (fil. 82) + (- a - 02 + ²⁵)“ = 20& - 0,5 a² +4002 - 02 - fil" - Q₂u + 25"

gdzie: u - mnożnik Lagrange’a, którego wartość odpowiada wartości zysku krańcowego dla optymalnych wielkości produkcji przy zmianie zdolności produkcyjnych w ograniczeniu.

Irena Woroniecka

Wydział Informatycznych Technik Zarządzania Wyższa Szkoła Informatyki Stosowanej i Zarządzania