20360

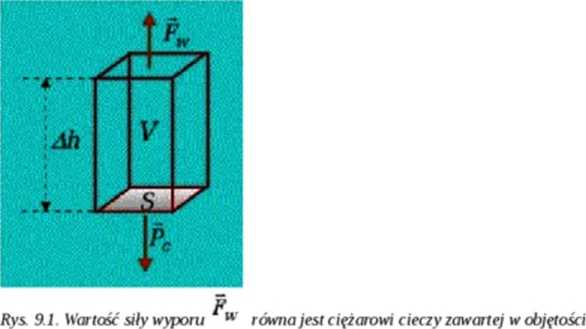
Wyróżnijmy w objętości cieczy prostopadłościan o wysokości b i polu podstawy .

V

s

Na wszystkie jego ścianki działa to samo

ciśnienie statyczne ^p0 równoważąc się wzajemnie. Gśiuenie hydrostatyczne jest jednak większe na ściankę dołnąniz górną. Różnica (patrz Rys 9.1.) wynosi ^ ‘^^c & . a siła z nią związana, zwana siłą wyponi jest skierowana pionowo do góry i jej

,.    Fu/ ~ S Ah Dr ' Z - V- p_r • B = m- S

wartość wynosi    ^w    c °    ^c °    °

Siłę tę równoważy skierowana w dół siła ciężaru samej cieczy zawartej w wyróżnionej objętości

^Pc = ^V Pc S=^m S

W rezultacie, ciecz pozostaje w spoczynku, czego należało oczekiwać.

P

różnym od ^c . to działająca w dół siła różni się od

Vg(p_c-p)    ₍₉₈₎

Kiedy jednak objętość ^ stanowi zanurzone w cieczy ciało o ciężarze ^P siły wyponi Różnica tych sił

fl= F„-P = V p_c g-V p g =

inoże być dodatnia, równa żeni bądź ujemna. Tym trzem przypadkom odpowiadajątrzy możliwości - ciałapływają w cieczy, pozostają na danej głębokości całkowicie zanurzone lub toną Wzór (9.8) wyraża sformułowane przez Archiraedesa (287 - 212 p n.e.) prawo Na ciało zanurzone w cieczy działa siła wyporu równa ciężarowi cieczy wypartej przez to ciało.

Należy zaznaczyć, że prawo to odnosi się także i do gazów stanowiąc podstawę latania balonów i sterowców - jak ten na fotografii obok.

Łl\Q\mamg-Łiagfe?iy

Ruch cieczy zwany przepływem może być określony przez podanie dla każdego punkm w cieczy wektora prędkości cieczy w funkcji czasu. Zbiór takich wektorów tworzy pole prędkości. Jeśli wektory prędkości są równoległe do kieninku przepływu to przepływ ten nazywamy laniiinriiyni Linie, do których równoległe są wektory prędkości nazywamy liniami prądu. Jeśli przepływ jest laminarny. to linie te nie przecinają się i zgodne są z torami cząstek cieczy. Pomszająca się w ten sposób ciecz tworzy stnimienie zwane też strugami lub rurkami prądu Nie następuje wtedy mieszanie się sąsiednich warstw cieczy. Cząstki cieczy poruszają się wewnątrz strugi me przecuiając jej bocznych ścianek. Kierunek strugi odpowiada kienmkom wektorów prędkości cząstek cieczy. Przepływ jest nirbiilentny jeżeli stmgi płynu mieszają się. Jeśli wektory prędkości cieczy zachowują stałe wartości w czasie, to przepływ taki nazywamy stacjonarnym. Wszystkie cząstki cieczy przepływające przez dany punkt mają wtedy ten sam wektor prędkości

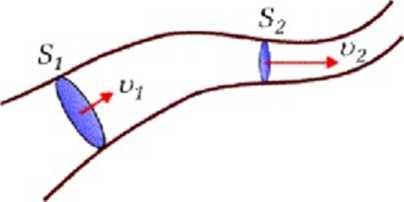
Rys. 9.3. Ilustracja równania ciągłości

s s

Rozpatrzmy przepływ stacjonarny i weźmy pod uwagę dwa przekroje stmgi * i 2 prostopadłe do jej kieninku. Jeśli ciecz jest nieściśliwa, to przez każdy z nich przepływa ta sama objętość płynu w danym odcinku czasu. Objętość ta równa jest

AV = Sj -Uj At . . : .    , i , , n

*    ¹    . gdzie ¹ jest równe ¹ lub • .

Z równości obu objętości wynika, że

^U*    (9.9)

Widać z niego, że prędkości cieczy w stnidze są

Sf uj = S2 ■ 1)2 lub

Związek ten. wyrażony tu na dwa sposoby, nosi nazwę równania ciągłości.