23294

Teoria informacji i kodowanie - Wykład nr 1

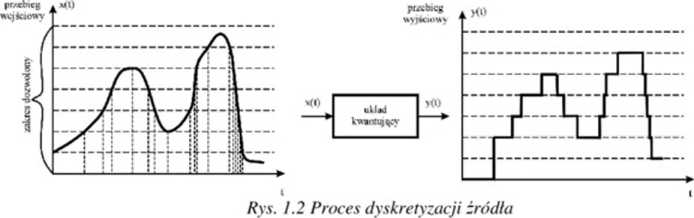
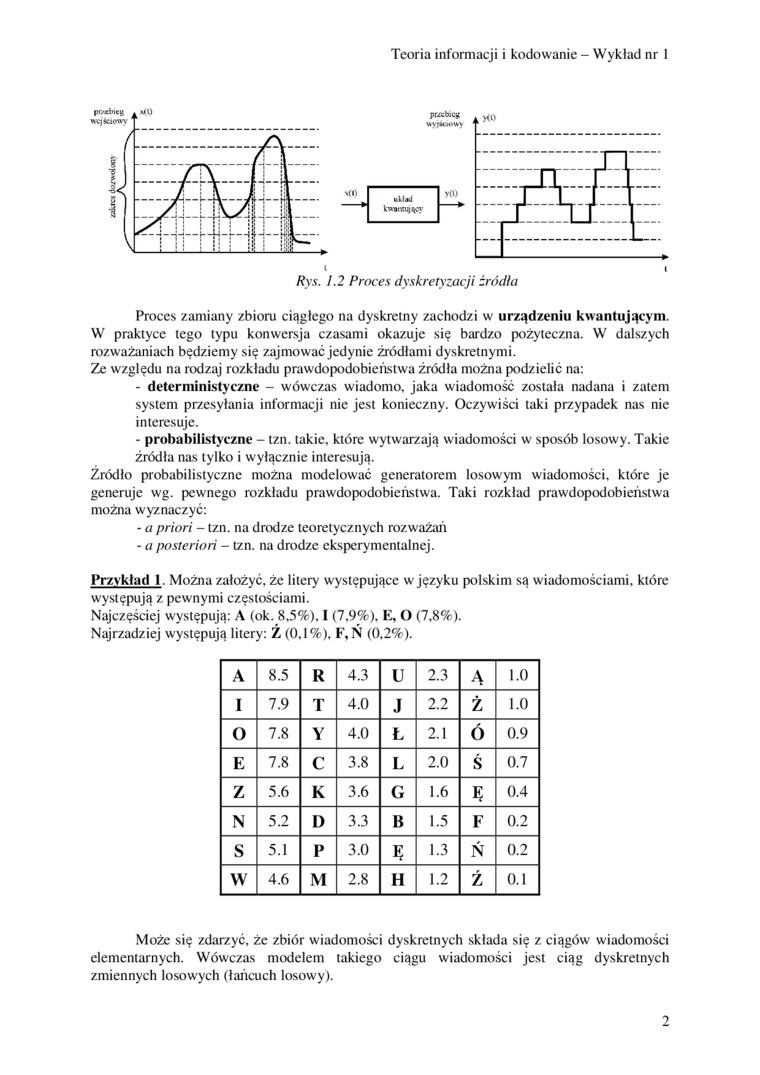
Proces zamiany zbioru ciągłego na dyskretny zachodzi w urządzeniu kwantującym. W praktyce tego typu konwersja czasami okazuje się bardzo pożyteczna. W dalszych rozważaniach będziemy się zajmować jedynie źródłami dyskretnymi.

Ze względu na rodzaj rozkładu prawdopodobieństwa źródła można podzielić na:

-    deterministyczne - wówczas wiadomo, jaka wiadomość została nadana i zatem system przesyłania informacji nie jest konieczny. Oczywiści taki przypadek nas nie interesuje.

-    probabilistyczne - tzn. takie, które wytwarzają wiadomości w sposób losowy. Takie źródła nas tylko i wyłącznic interesują.

Źródło probabilistyczne można modelować generatorem losowym wiadomości, które je generuje wg. pewnego rozkładu prawdopodobieństwa. Taki rozkład prawdopodobieństwa można wyznaczyć:

-    a priori - tzn. na drodze teoretycznych rozważań

-    a posteriori - tzn. na drodze eksperymentalnej.

Przykład 1. Można założyć, że litery występujące w języku polskim są wiadomościami, które występują z pewnymi częstościami.

Najczęściej występują: A (ok. 8.5%). I (7,9%), E, O (7,8%).

Najrzadziej występują litery: Ź (0,1%), F,Ń (0,2%).

A	8.5	R	4.3	U	2.3	Ą	1.0
I	7.9	T	4.0	J	2.2	Ż	1.0
O	7.8	Y	4.0	Ł	2.1	ó	0.9
E	7.8	C	3.8	L	2.0	ś	0.7
Z	5.6	K	3.6	G	1.6	Ę	0.4
N	5.2	I)	3.3	B	1.5	F	0.2
S	5.1	P	3.0	Ę	1.3	Ń	0.2
W	4.6	M	2.8	H	1.2	Ź	0.1

Może się zdarzyć, że zbiór wiadomości dyskretnych składa się z ciągów wiadomości elementarnych. Wówczas modelem takiego ciągu wiadomości jest ciąg dyskretnych zmiennych losowych (łańcuch losowy).

2