36633

Gdy atom (a więc i jego moment magnetyczny) umieścimy w zewnętrznym polu magnetycznym to wektor momentu magnetycznego (a więc i wektor momentu pędu) będzie wykonywał ruch precesyjny wokół linii pola magnetycznego. Okazuje się, że zgodność z empirią (tzw. Efekt Zeemana) wymaga jeszcze jednego kwantowania - mianowicie dopuszczalne sa tylko niektóre kąty a pomiędzy wektorami B oraz L (lub u) Skwantowany jest wiec rzut wektora Lna oś 'z' czyli kierunek linii pola B : ^ _ £_cos a _

m - to tzw MAGNETYCZNA LICZBAKWANTOWA; jej możliwe wartości to całkowite (dodatnie i ujemne)liczby od -I do +INp.: dla liczby orbitalnej I = 2 mamym= -2,-1, 0,+1,+2, a więc 5 dozwolonych orientacji wektora L oraz płaszczyzny orbity elektronu w przestrzeni. Nazywa się to KWANTOWANIEM PRZESTRZENNYM.

Gdy atom umieszczony jest w zewnętrznym polu magnetycznym to każdej Liczbie kwantowej m odpowiada nieco inna wartość energii. Tak więc energia Poziomu energetycznego zależy już teraz od trzech liczb kwantowych: n, I, m. Kolejne, coraz dokładniejsze dane empiryczne (dotyczące struktury linii widmowych) wskazały na konieczność przypisania cząstkom elementarnym (a więc i elektronom) tzw. SPINOWEGO MOMENTU PĘDU -    . Jest to własny moment pędu elektronu niezależny od momentu orbitalnego. Jest on

też skwantowany według reguły:    = h^[s(s +1) j

^L‘~~^k

gdzie s to tzw SPINOWA LICZBA KWANTOWA. która ma tylko jedną możliwą wartość liczbową: s = H. Stąd całkowity spinowy moment pędu elektronu ma także tylko jedną możliwą wartość:

Ze spinowym momentem pędu elektronu związany jest także SPINOWY MOMENT MAGNETYCZNY:

e i    *-

m,    2m.

Spinowy moment magnetyczny (oraz spinowy moment pędu) są również skwantowane przestrzennie - rzut spinowego momentu pędu na wybrany kierunek osi 'z' jest:

= s. = m.h = ± — h 2

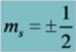
gdzie m_t to spinowa magnetyczna liczba kwantowa:

2.Stmktura okresowego układu pierwiastków w kontekście modelu Sommerfelda i występujących w nim liczb kwantowych; zapełnianie kolejnych powłok elektronowych w atomach wieloelektrodowych.