4538

Konrad Kubiec

Teoria Kategorii i jej zastosowanie w informatyce

sposób:

Fakt 1.2 [uczby naturalne kategoryjnie]

Zbiór liczb naturalnych N jest to zbiór zawierający liczbę zero oraz wyposażony w funkcję suce (tj) : N —» N taką, że: dla dowolnego zbioru X i elementu <* E X oraz funkcji 9 X —* X

istnieje dokładnie jedna funkcja / : N —> X spełniająca dwa warunki: /(o) = ^e oraz / o suce = go f

Dwa powyższe Fakty wskazują na to, że definicje teorii mnogości można wyrażać operując jedynie pojęciem funkcji i złożenia funkcji (zauważmy, że elementy zbiorów można traktować jako funkcje, których dziedziną jest singleton). Postawmy więc śmiałe pytanie: czy można prezentować różnorodne teorie matematyczne badając jedynie własności przekształceń obiektów matematycznych będących przedmiotem zainteresowania danej teorii? A zatem pytamy czy: można prezentować teorię mnogości badając własności funkcji między zbiorami, teorię grup badając własności homomorfizmów grup, topologię badając własności funkcji ciągłych pomiędzy przestrzeniami topologicznymi? W ogólności zapytajmy czy można badać dowolne obiekty matematyczne z określoną strukturą za pomocą własności przekształceń, które tę strukturę zachowują?

Odpowiedź brzmi: tak - i ta właśnie twierdząca odpowiedź powołuje do życia teorię kategorii. Teoria kategorii składa się bowiem z twierdzeń dotyczących uniwersalnych własności przekształceń, niezależnych od cech szczególnych danych teorii matematycznych. Tak więc, teoria kategorii bada wspólne, uniwersalne własnościami zbiorów, grup, przestrzeni topologicznych, przestrzeni wektorowych, częściowych porządków, i tak dalej, wszystko w języku przekształceń danej struktury.

Saunders Mac Lane (1909-2005)

Czy da się krótko, nieformalnie zebrać najważniejsze cechy przekształceń - cechy niezależne od konkretnej teorii matematycznej? Posługując się Teorią kategorii - tak. Zaczynamy od nazwy: przekształcenie nazywać będziemy również morfizmem (bo w przeróżnych teoriach matematycznych natykamy się na homomorfizmy, homeomorfizmy, endomorfizmy. itd.) lub po prostu strzałką (bo tak zwykle graficznie przedstawia się przekształcenia). Przekształcenie działa pomiędzy obiektami, np. funkcja to przekształcenie zbiorów, homomorfizm to przekształcenie gripy w grupę, funkcja ciągła to przekształcenie przestrzeni topologicznej w przestrzeń topologiczną, funkcja monotoniczna to przekształcenie posetu w poset itd. (Załóżmy na początku dla prostoty, że w naszych przykładach nie bierzemy pod uwagę przekształceń obiektów pewnej klasy w obiekty innej klasy, na przykład wyznacznika, który przekształca macierz w liczbę. Takimi morfizmami zajmiemy się później.) Każde przekształcenie / działa na pewien jedyny obiekt nazwijmy go dziedziną / i oznaczmy ^^OIIl(/), i przekształca go w inny jedyny obiekt nazywany przeciwdziedziną f i oznaczany jako cod(/).

Fakt, że

morfizm / ma dziedzinę A i przeciwdziedzinę B zapisujemy:

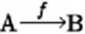
lub po prostu / ^: A —» B. Nasza teoria nie może istnieć bez pojęcia złożenia przekształceń: zakładamy, że dwóm morfizmom f->9 takim, że cod($) = dom(/) (strzałki takie nazywamy

2