5106

Ifflfctcz w.fięft. Rynki finansowe, atii li ręk oka&mięh. 2004 200^

gdzie:    R₍₎ - wartość inwestycji w okresie początkowym, P, - wartość inwestycji w okresie następnym.

d, - dodatkowe dochody z inwestycji wypłacone w okresie, za który obliczana jest stopa zwrotu (np. z tytułu

P —P

iloraz '    ⁰ 100

Po

dywidend). Przy takich oznaczeniach różnica P, —P_f) oznacza zysk kapitałowy.

d_x

oznacza stopę zysku kapitałowego, natomiast —-100 - stopę dywidendy.

Po

Upraszczając zagadnienie założymy, że stopa zwrotu w badanym okresie przyjmować może skoiiczoną liczbę wartości ze znanymi prawdopodobieństwami. Zatem:

P, R₂ ••• R_n

P, P₂ P_n

gdzie prawdopodobieństwa P_y spełniają 0 ^ P, ^1 oraz . P, =1.

Zapisane powyżej przyporządkowane wartościom stopy zysku R, prawdopodobieństw icli wystąpienia P/ określamy rozkładem prawdopodobieństwa. Przyporządkowane to przedstawia szanse otrzymania różnych stóp zwrotu z inwestycji. Zwykle prawdopodobieństwa te nie są równe, zatem rozkład prawdopodobieństwa stóp zwrotu nie jest jednostajny. W rzeczywistości stopy zwrotu są ciągłe, w tym sensie, że można określić prawdopodobieństwo zdarzenia polegającego na tym. że stopa zwrotu przyjmie wartości rzeczywiste z pewnego przedziału. Rozkład prawdopodobieństwa opisuje funkcja gęstości rozkładu.

Przykład 1

Na następny miesiąc rozpatrywanych jest 5 wariantów rozwoju sytuacji na rynku: 1 - bardzo niekorzystny, 2 -gorszy niż przeciętnie. 3 - przecięny. 4 - lepszy niż przeciętnie. 5 - wyjątkowo korzystny. Prawdopodobieństwa wystąpienia tych stanów oraz spodziewane stopy zwrom w przypadku zrealizowania się danego stanu są następujące:

i?, = -1,0% R_: = 0.0% K, = 10% R, = 2,0% Rr, = 30% R_(i = 4.0%

P, =0,05 P₂ =0,10 P₃ =0,30 P, =0,30 P₅ =0,20 P₆ =0,05

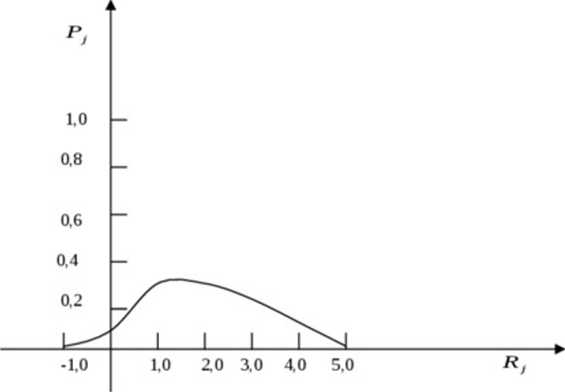
Rysimek 1 pokazuje rozkład prawdopodobieństwa stopy zwrotu.

Rysunek 1. Rozkład prawdopodobieństwa stopy zwrotu

2