Laboratorium z Fizyki

Sprawozdanie z ćwiczenia nr 21

Temat: ”Pomiar ciepła właściwego ciał stałych”

Wykonał:

Andrzej Kotwica

I Elektronika

1. Cel doświadczenia

Celem doświadczenia jest zapoznanie się z techniką pomiarów kalorymetrycznych oraz ocena dokładności tych pomiarów.

2. Część teoretyczna

a) Kalorymetria i budowa kalorymetru

KALORYMETRIA - jest to dział nauki o cieple zajmujący się mierzeniem ilości ciepła . Opiera się ona na kilku zasadach , które wyrażają się następująco :

1) Ilość ciepła Qoddana przez ciało badane jest równa ilości ciepła Qpobranej przez ciała otaczając

Q=Q (w 1.1)

2) Ilość ciepła pobrana przez ciało podczas ogrzewania jest równa ilości ciepła oddanej podczas ostygania w tym samym zakresie temperatur jeśli ciało przechodzi w odwrotnym porządku przez te same stany pośrednie. Przyjmując, że ciała pobierające bądź oddające ciepło nie wykonują pracy , ani też na nich nie jest wykonywana praca, powyższy wzór stanowi Zasadę zachowania energii lub nosi nazwę Równania bilansu cieplnego.

3) Ilość ciepła Q pobrana bądź oddana przez ciało jednorodne jest proporcjonalna do jego masy, a przy niewielkich zmianach temperatury- do przyrostu temperatury:

Q = c m t (w 1.2)

Aby stosować zasadę zachowania energii w jakiejkolwiek postaci, należy utworzyć układ izolowany , tzn. taki, który nie wymienia energii z otoczeniem . W kalorymetrii rolę takiego urządzenia spełnia kalorymetr, którego właściwości izolacyjne nie są idealne, tzn. niewielkie i niemożliwe do określenia ilości ciepła przenikają na zewnątrz kalorymetru. Wymiana ciepła z otoczeniem wpływa przede wszystkim na końcową temperaturę kalorymetru.

BUDOWA KALORYMETRU

Rys 1

K- Naczynie kalorymetryczne

N- Pokrywa kalorymetru

T- Termometr

B- Naczynie z wodą o podwójnych ściankach

M.- Mieszadełko

Mieszadełko (M.) powoduje równomierne ogrzewanie lub ochładzanie wody. Jest ono umieszczone w naczyniu kalorymetrycznym (K), które ustawione jest na nóżkach źle przewodzących ciepło (drewno, korek). Wszystko to znajduje się wewnątrz naczynia (B) .Bardzo często posrebrza się i poleruje zewnętrzną powierzchnie naczynia kalorymetrycznego(K) w celu utrudnienia wymiany ciepła z otoczeniem przez promieniowanie. Uchwyt mieszadełka i pokrywa kalorymetru (N) powinny być wykonane z materiału źle przewodzącego ciepło. Pokrywa (N) chroni naczynie kalorymetryczne przed odpływem ciepła konwekcję oraz przed parowaniem.

b) Wyznaczanie ciepła właściwego ciał stałych

Ciepło właściwe c jest to stosunek ilości ciepła Q pobranego przez to ciało do iloczynu masy ciała m i przyrostu temperaturyt

W układzie SI ciepło właściwe mierzymy w następujących jednostkach:

Ciepło właściwe ciała stałego wyznaczamy z bilansu cieplnego ułożonego dla wymiany ciepła między tym ciałem ogrzanym do pewnej temperatury a kalorymetrem wypełnionym wodą o niższej temperaturze. Ilość ciepła oddana przez badane ciało o masie m_c ochłodzone od temperatury początkowej T_c do końcowej T_k wynosi:

c_x-szukane ciepło właściwe

Ciepło pobrane przez wodę

c_w- ciepło właściwe wody

m_w- masa wody

T_w- temperatura początkowa wody w kalorymetrze

T_k- temperatura końcowa

Ciepło pobrane przez naczynie kalorymetryczne oraz przez mieszadło(wykonane z tego samego metalu)

c_k- ciepło właściwe metalu, z którego wykonane jest naczynie kalorymetryczne i mieszadło

m_k- masa naczynia kalorymetrycznego razem z mieszadłem

W bilansie cieplnym należy również uwzględnić ciepło, które pobiera termometr. Stwierdzono, że jednostka objętości rtęci pobiera podczas ogrzania o jeden stopień w przybliżeniu taką samą ilość ciepła, jak jednostka objętości szkła. Ilość ta wynosi:

wobec tego

V- objętość zanurzonej części termometru

Równanie bilansu cieplnego ma zatem postać:

Z powyższego równania możemy wyliczyć szukane ciepło właściwe

3.Część praktyczna

a) Tabela pomiarów dla ciała nr 1

nr	R	R	V	V	Tc	Tw	Tk	Tc,
pomiaru	J/	kg K	10^-6	m^3		K
1	1,93 10^6	0,08 10^6	2	0,2	343,95	290,05	293,05	0,1

R - objętościowe ciepło właściwe szkła i rtęci

V - objętość zanurzonej części termometra

T_c- temperatura początkowa badanego ciała

T_w- temperatura początkowa wody w kalorymetrze

T_k- temperatura końcowa

Nr	mk	mk+w	mw	mc	mc	cw	ck	cx	cx	cw	ck		cx
			kg				J/	kg	K			%	k kal /kg K
1	1,271	2,271	1,5	0,6785	0,0001	4186	384	359,99	18,822	8	1	5,23	85,98 10^-3

Temperatura wody przed wrzuceniem badanego ciała

t	min	1	2	3	4	5	6	7	8	9	10
T	C	17,4	17,4	17,5	17,5	17,6	17,6	17,6	17,7	17,8	17,8

Temperatura wody po wrzuceniu badanego ciała

t	s	10	20	30	40	50	60	70	80	90	100
T	C	19,2	19,5	19,8	19,9	19,9	19,9	19,9	19,9	19,9	19,9

Przykłady obliczeń:

1. Ciepło właściwe ciała pierwszego obliczamy ze wzoru 1.9

2. Błąd c_x obliczamy na podstawie wzoru 1.9 metodą różniczki zupełnej

oznaczając

= 0,053

, , ,

c_x = 0,636 + 0,022 + 0,067 + 0,053 + 0,641 + 17,192 + 0,002 + 0,00848 + + 0,02 + 0,231 = 18,822

c_x = 359,99 18,822

b) Tabela pomiarów dla ciała nr 2

nr	R	R	V	V	Tc	Tw	Tk	Tc,
pomiaru	J/	kg K	10^-6	m^3		K
1	1,93 10^6	0,08 10^6	2	0,2	343,15	290,95	293,00	0,1

Nr	mk	mk+w	mw	mc	mc	cw	ck	cx	cx	cw	ck		cx
			kg				J/	kg	K			%	k kal /kg K
1	1,271	1,771	1,5	0.,085	0,0001	4185	384	818,47	42,946	8	1	5,247	85,98 10^-3

Temperatura wody po wrzuceniu badanego ciała (II)

t	s	10	20	30	40	50	60	70	80	90	100
T	C	17,7	18,5	19,0	19,4	19,5	19,6	19,6	19,7	19,7	19,7

Przykłady obliczeń :

1.Obliczenia ciepła właściwego ciała drugiego (II)

2.Sposób obliczenia jak w poprzednim przykładzie

a=0,121

c_x=1,452+0,05+0,154+0,265+1,454+38,975+0,0046+0,019+0,0467+0,526=

=42,9463

3.Cipło właściwe obliczone w innych jednostkach

C_x=195,49 10^-3

4.Obliczanie błędu względnego, procentowego C_x ciepła właściwego korzystając ze wzoru :

C_x ==

Wnioski:

Celem ćwiczenia było wyznaczenie ciepła właściwego dwóch próbek metalu . Podczas przeprowadzania doświadczenia zaobserwowaliśmy zjawisko wymiany ciepła pomiędzy próbką metalu a cieczą . Okazało się , że ciało nagrzane do temperatury znacznie większej niż temperatura cieczy „ odda” swoją temperaturę cieczy , tak żeby nastąpiła równowaga . Po napisaniu bilansu cieplnego mogliśmy wyznaczyć ciepło właściwe . Metoda ta opatrzona jest pewnym błędem , który zależy od kilku czynników. Po pierwsze: nie uwzględniliśmy wymiany ciepła jaka się dokonała podczas przeniesienia próbki z podgrzewacza do kalorymetru (było to trudne do zrealizowania). Po drugie: odczyt pomiarów mógł być niedokładny ze względu na dość gwałtowne skoki temperatury podczas ochładzania próbki, jednak nie wpłynęły one znacząco. Pomimo różnych mas próbek temperatura końcowa była taka sama to znaczy prawie 20°C. W obu przypadkach, po wrzuceniu ich do wody temperatura gwałtownie podskoczyła, po czym ustaliła się osiągając wartość niższą niż temperatura otoczenia.

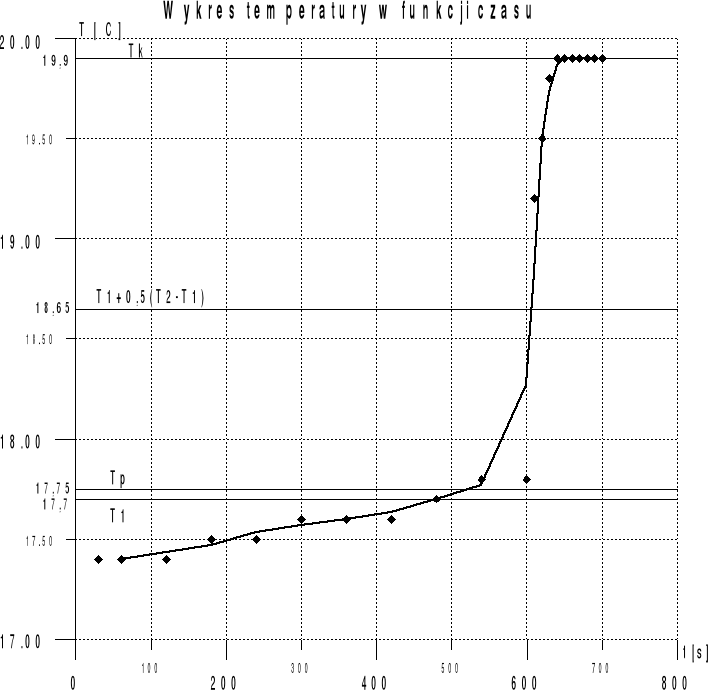
W doświadczeniu otrzymaliśmy błędy względne rzędu 5%. Jest to niedużo ,także

możemy powiedzieć ,że wyznaczanie ciepła właściwego metodą kalorymetryczną jest dokładną metodą. Wykres jaki otrzymaliśmy z pomiarów dokładnie obrazuje przebieg doświadczenia. Nie jest on jednak idealny, gdyż w końcowym etapie temperatura w kalorymetrze nie zmniejszała się lecz pozostawała stała. Było to spowodowane tym ,że temperatura otoczenia była wyższa od temperatury wody. Jednak najważniejsza część wykresu, czyli gwałtowny wzrost temperatury, został przedstawiony wyraźnie.

---