I PRACOWNIA FIZYCZNA
ĆWICZENIE: 59
Badanie pętli histerezy mgt. przy pomocy oscyloskopu.
Goncerz Rafał
1. WSTĘP TEORETYCZNY
Diamagnetyki
Substancje w których momenty magnetyczne atomów są - w przypadku braku zewnętrznego pola magnetycznego - równe zeru ,gdyż momenty magnetyczne wszystkich elektronów w atomie są wzajemnie skompensowane
Paramagnetyki
Substancje , których atomy w przypadku braku zewnętrznego pola magnetycznego mają różny od zera moment magnetyczny. Występowanie tego momentu magnetycznego może być związane zarówno z orbitalnym ruchem elektronów w atomach paramagnetyka , jak i ze spinowymi momentami tych elektronów.
Ferromagnetyki
Ciała stałe ( z reguły substancje krystaliczne ) , wykazujące przy niezbyt wysokich temperaturach własne namagnesowanie , które silnie zmienia się pod wpływem oddziaływań zewnętrznych pola magnetycznego , deformacji , zmiany temperatury . Ferromagnetyki - w odróżnieniu od słabo magnetycznych diamagnetyków i paramagnetyków - stanowią silnie magnetyczne ośrodki ; pole magnetyczne w nich może setki lub tysiące razy przewyższać pole zewnętrzne .
Do wykorzystania na magnesy trwałe wykorzystywane są ferromagnetyki twarde , które mają szeroki kształt pętli histerezy magnetycznej .
2. WYNIKI POMIAROW
OPRACOWANIE WYNIKOW
Korzystając ze wzorów na :
Natężenie pola magnetycznego
![]()
gdzie :
Ux - napięcie odczytane z oscyloskopu
n1 = 330±1 - ilość zwojów uzwojenia pierwotnego
R1 = (180,6±1%)
L = (22,4±0,02)cm
Indukcja magnetyczną
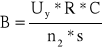
gdzie :
Uy
n2 = 45±1
R = (4,7±1%) kΩ
C = (56,3±5%) μF
Oraz z metody różniczki zupełnej obliczam niepewności pomiarowe
ΔH = H*(ΔUx/Ux+Δn/n+ΔR1/R1+Δl/l)
ΔB = B*(ΔUy/Uy+ΔR/R+ΔC/C+Δn/n +ΔS/S)
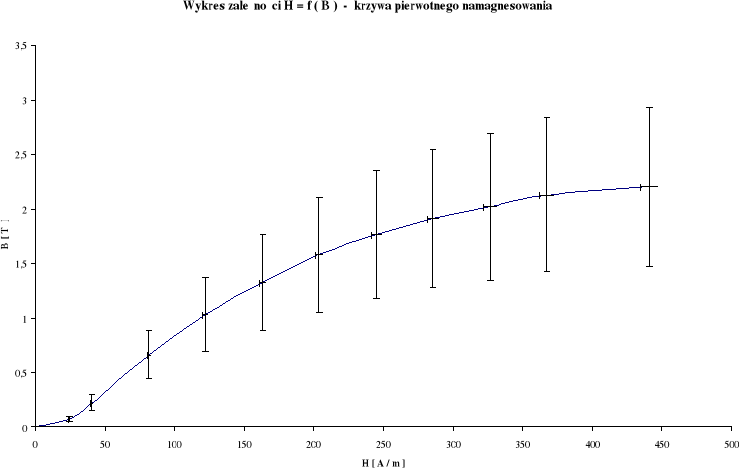
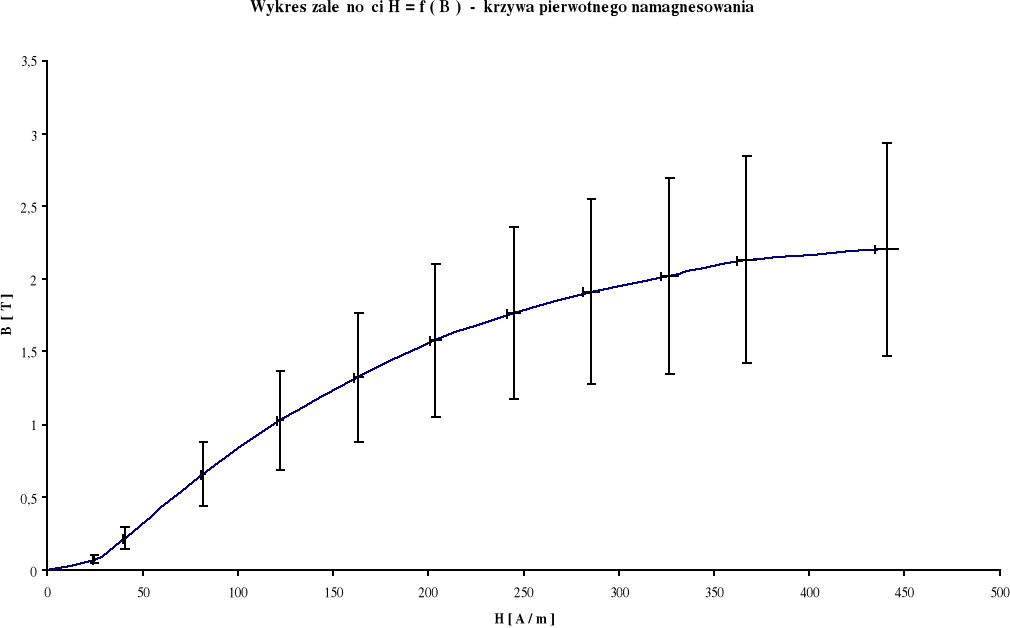
obliczam wartości H i B dla wierzchołków pętli histerezy :
Ux |
Uy |
H |
B |
ΔH |
ΔB |
54 |
0,6 |
440,5 |
2,21 |
6,13 |
0,73 |
45 |
0,58 |
367,08 |
2,13 |
5,11 |
0,71 |
40 |
0,55 |
326,29 |
2,02 |
4,54 |
0,67 |
35 |
0,52 |
285,51 |
1,91 |
3,98 |
0,64 |
30 |
0,48 |
244,72 |
1,76 |
3,41 |
0,59 |
25 |
0,43 |
203,93 |
1,58 |
2,84 |
0,53 |
20 |
0,36 |
163,15 |
1,32 |
2,27 |
0,44 |
15 |
0,28 |
122,36 |
1,03 |
1,7 |
0,34 |
10 |
0,18 |
81,57 |
0,66 |
1,14 |
0,22 |
5 |
0,06 |
40,79 |
0,22 |
0,57 |
0,07 |
3 |
0,02 |
24,47 |
0,07 |
0,34 |
0,03 |
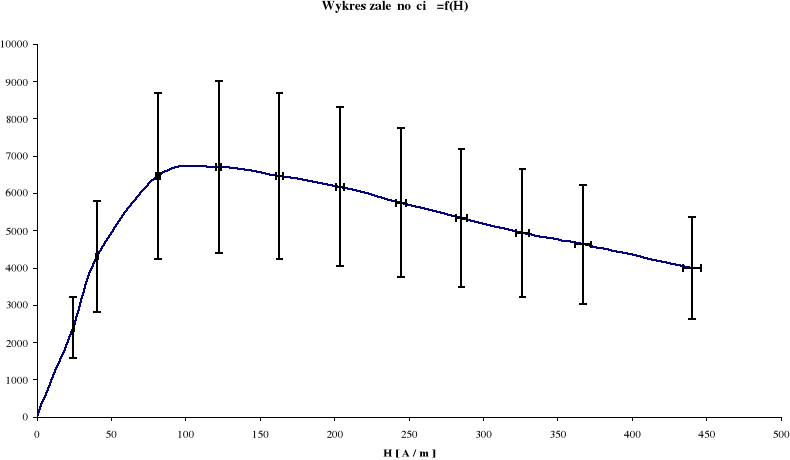
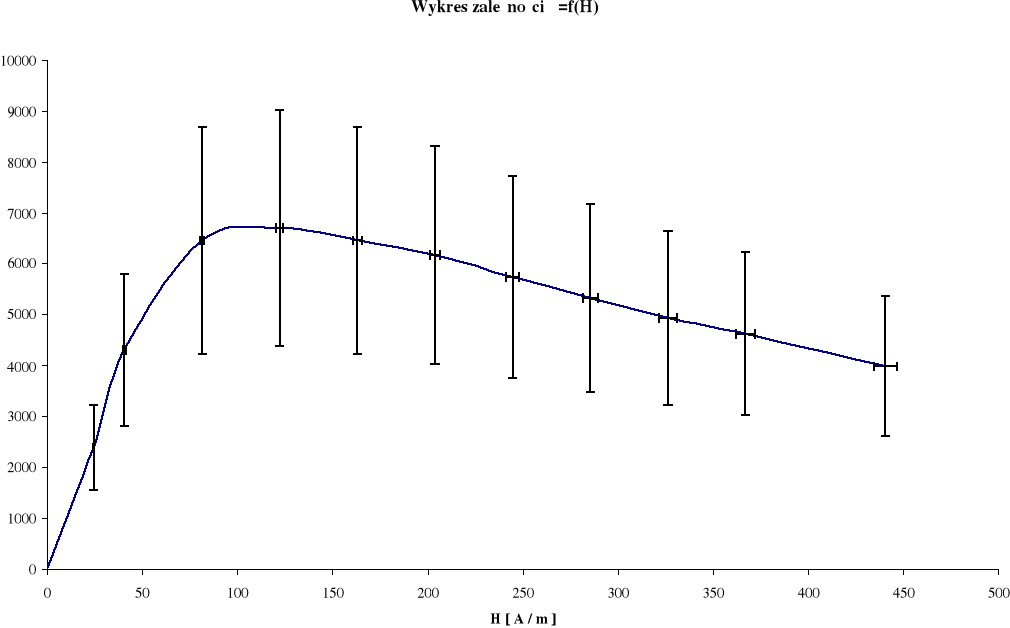
Obliczam wartość względnej przenikalności magnetycznej μ korzystając z wzoru:
![]()
gdzie: μo = 4π⋅10-7 [NA-2]
Niepewność pomiarową Δμ obliczam metodą pochodnej logarytmicznej:
Δμ = μ(ΔB/B+ΔH/H)
Otrzymałem następujące wyniki:
μ |
Δμ |
3983,577 |
1379,251 |
4620,949 |
1599,931 |
4929,677 |
1706,823 |
5326,612 |
1844,255 |
5736,351 |
1986,121 |
6166,577 |
2135,08 |
6453,395 |
2234,386 |
6692,41 |
2317,141 |
6453,395 |
2234,386 |
4302,263 |
1489,591 |
2390,146 |
827,5504 |
μ max |
Δ μ max |
6692,41 |
2317,141 |
3. WNIOSKI
Ćwiczenie przeprowadzono tylko dla jednej wartości oporu - dlatego nie mogę porównać wyników oraz kształtu różnych pętli histerez mgt. Na wartość błędów pomiarowych miał również wpływ stopień dokładności pomiarów , lecz największy wpływ miało sumowanie się poszczególnych błędów pomiarów z błędami wynikającymi z przybliżeń przyjętych do obliczeń. Wartość tablicowa μ dla materiałów wykorzystywanych do produkcji rdzeni transformatorów wynosi dla stali miękkiej mgt. od 1000 do 27000 dla ferrokobaltu, który wykorzystywany jest w transformatorach specjalnego przeznaczenia. Najczęściej jednak wykorzystywana jest stal o μ w granicach 1000 - 9000, wobec czego wyniki uzyskane w ćwiczeniu mieszczą się w tych granicach.
![]()
![]()
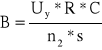
Wyszukiwarka
Podobne podstrony:
PRAC1FIZ, LAB60, I PRACOWNIA FIZYCZNA
więcej podobnych podstron