Cel ćwiczenia:

Pomiar zależności oporności elektrycznej (rezystancji) metalu (platyny) i półprzewodnika (NTC 210) od temperatury, wyznaczenie temperaturowego współczynnika oporności metalu i przerwy energetycznej półprzewodnika.

Wprowadzenie:

Ciała stałe ze względu na ich własności elektryczne można podzielić na trzy grupy: przewodniki, półprzewodniki i dielektryki (izolatory). Do półprzewodników należą ciała, których przewodność właściwa jest mniejsza od przewodności dobrych przewodników, ale znacznie większa od przewodności dielektryków i wynosi od 10^-8 do 10⁵ Ω^-1m^-1. Różnice w strukturze elektronowej są przyczyną różnic we własnościach elektrycznych, optycznych i innych tych ciał. O przewodnictwie ciał stałych decyduje ilość elektronów walencyjnych w paśmie przewodnictwa. Ilość tę reguluje szerokość pasma wzbronionego (przerwy energetycznej 0.1 ÷ 2 eV) oraz ewentualne domieszki. W przewodniku samoistnym koncentracja swobodnych elektronów wykładniczo zależy od temperatury :

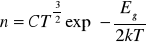
Energia aktywacji (1/2 E_g) jest energią progową, gdyż po jej przekroczeniu następuje szybki wzrost ilości elektronów w paśmie przewodnictwa. Zależność koncentracji nośników od temperatury jest specyficzną właściwością półprzewodników, odróżniającą je od metali. Przejście elektronu z pasma walencyjnego do pasma przewodnictwa oznacza pojawienie się w paśmie podstawowym wolnego stany zwanego dziurą, którą mogą zająć elektrony z niższych poziomów energetycznych. Powstaje zatem swoisty ruch dziur w kierunku jądra atomowego, odpowiedzialny za przewodzenie części prądu płynącego przez ciało. W półprzewodniku samoistnym udział prądu dziurowego i elektronowego jest taki sam.

W półprzewodniku domieszkowanym akceptorowo (czyli domieszki III grupy atomowej np.: Ga czy Al.) przewodnictwo jest dziurowe, gdyż tuż nad pasmem walencyjnym powstaje akceptorowy poziom energetyczny obsadzony przez dziury domieszki. Dzięki temu już przy niewielkiej energii (rzędu 0,001eV ÷ 0,01eV) elektrony z pasma podstawowego mogą przejść na nowy poziom, umożliwiając tym samym ruch dziur w paśmie podstawowym.

W półprzewodniku typu n (z domieszkami donorowymi - V grupa atomowa np.: P i As) występuje przede wszystkim przewodnictwo elektronowe, ponieważ dodana domieszka powoduje powstanie nowego poziomu tuż pod pasmem przewodnictwa, obsadzonego przez nadmiarowe elektrony z domieszki. I znów przy niewielkiej dostarczonej energii następuje przejście elektronów z nowego poziomu do pasma przewodnictwa.

W półprzewodnikach domieszkowanych po przekroczeniu pewnej granicznej temperatury, następuje gwałtowny przyrost standardowego generowania par dziura - elektron (tak jak w półprzewodniku samoistnym), które w niższych temperaturach było mało znaczące w stosunku do przewodnictwa domieszkowego. Z ilością nośników oraz ich ruchliwością związane jest pojęcie przewodności właściwej (konduktywności) danego materiału :

Wraz ze wzrostem temperatury w półprzewodnikach następuje spadek rezystancji.

W metalach swobodnymi nośnikami ładunku są elektrony nie zapełnionego pasma przewodnictwa. Ich ilość w znacznie mniejszym stopniu zależy od temperatury niż w półprzewodnikach i jest o kilka rzędów mniejsza. Brak pasma wzbronionego uniezależnia ilość przewodzących elektronów od przyłożonej energii. Istnieje jednak zjawisko rozpraszania elektronów przewodzących na defektach sieci lub na drgających jej atomach. W wysokich temperaturach amplituda drgań sieci jest duża, więc maleje ruchliwość elektronów i co za tym idzie przewodność metali. Natomiast w niskich temperaturach przeważa rozpraszanie na defektach sieci. Konduktancja metali wyraża się wzorem:

Metoda pomiaru:

W komorze pomiarowej umieszczono badane próbki oraz termometr. Następnie przy pomocy grzejnika całość była podgrzewana. Pomiary wykonywano od temperatury 21 ÷ 90 ⁰C odczytując wyniki co 5 ⁰C, zarówno przy wzroście jak i spadku temperatury.

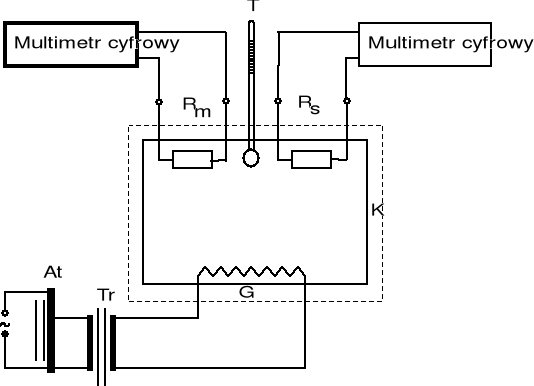
Układ pomiarowy:

At - Autotransformator

Tr - Transformator separacyjny

G - Grzejnik

T - Termometr

K - Komora

Rm - Rezystor metalowy (platyna)

Rs - Rezystor półprzewodnikowy (NTC 210)

Wyniki pomiarów:

Tabela: Wynik pomiaru rezystancji metalu i półprzewodnika w przypadku wzrostu temperatury.

Tem [^0C]	T [K]	1/T [1/k]	Rm. [Ω]	Rp [KΩ]	LnRp
21	294	0,003401	108,1	12,43	2,5201
25	298	0,003355	110,2	10,06	2,3086
30	303	0,0033	112,2	8,08	2,0894
35	308	0,003246	114,2	6,54	1,8779
40	313	0,003194	116,2	5,29	1,6658
45	318	0,003144	118,4	4,26	1,4492
50	323	0,003095	120,5	3,49	1,2499
55	328	0,003048	122,7	2,84	1,0438
60	333	0,003003	124,7	2,34	0,8502
65	338	0,002958	126,7	2,01	0,6981
70	343	0,002915	129,0	1,613	0,4781
75	348	0,002873	131,0	1,356	0,3045
80	353	0,002832	133,0	1,14	0,131
85	358	0,002793	135,0	0,962	-0,0387
90	363	0,002754	137,2	0,81	-0,2107

Tabela: Wynik pomiaru rezystancji metalu i półprze wodnika w przypadku spadku temperatury.

Tem [^oC]	T [K]	1/T [1/k]	Rm. [Ω]	Rp [KΩ]	LnRp
21	294	0,003401	107,1	13,72	2,6188
25	298	0,003355	108,5	11,8	2,468
30	303	0,0033	110,2	9,83	2,285
35	308	0,003246	112,1	8,07	2,088
40	313	0,003194	114,2	6,53	1,8764
45	318	0,003144	116,5	5,35	1,677
50	323	0,003095	119,2	3,79	1,3323
55	328	0,003048	121,7	3,03	1,1085
60	333	0,003003	123,8	2,5	0,9162
65	338	0,002958	125,7	2,08	0,703
70	343	0,002915	127,8	1,744	0,5661
75	348	0,002873	129,8	1,468	0,3839
80	353	0,002832	131,9	1,232	0,2086
85	358	0,002793	134,0	1,039	0,03825
90	363	0,002754	136,5	0,845	-0,1684

Opracowanie wyników:

Należało wykonać wykresy: dla półprzewodnika lnR_p=f(1/T) a dla metalu R_m.=f(T)

Dla półprzewodnika należało wyznaczyć w zakresie przewodnictwa samoistnego szerokość przerwy energetycznej korzystając z zależności:

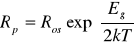
traktując przy tym R_os jako stałą. Po przekształceniach otrzymujemy zależność:

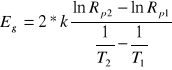
z której po podstawieniu danych z wykresu gdzie: T₁=363 K, T₂=294 K, lnR_p1= -0.2097 , lnR_p2=2.5201 , k=1.38054*10^-23 J/K- stała Boltzmanna, otrzymujemy zależność:

Przy czym wiadomo że: 1eV=1.6*10^-19J stąd wynika że: E_g≈0.728 eV ±ΔE_g

Dla metalu należało wyznaczyć temperaturowy współczynnik rezystancji korzystając z zależności:

gdzie po podstawieniu danych z wykresu : R_t=137.2 Ω, R₂₁=108.5 Ω otrzymujemy zależność:

Rachunek błędów:

Całkowite błędy otrzymanych wyników pochodzą z błędu pomiaru rezystancji i temperatury. Obliczę je korzystając z metody różniczki zupełnej:

Dla współczynnika rezystywności metalu wzór wygląda następująco :

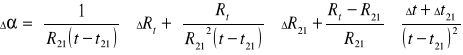
przy czym: Δt i Δt₂₁ = 0,5 K- błędy powstałe z niedokładności odczytu temperatury

oraz ΔR_t =0.986 i ΔR₂₁ =0.8405 - błędy bezwzględne powstałe z błędu pomiaru. Dla powyższych wartości otrzymujemy błąd bezwzględny pomiaru współczynnika równy :

Δα=0,00037513≈0,0004 [1/K]

Zatem błąd względny wynosi δα=9.8%.

Ostatecznie temperaturowy współczynnik oporności ma wartość:

α≈0,0038±0,0004[1/K]

Dla przerwy energetycznej wzór wygląda następująco :

przy czym: Δt i Δt₂₁ = 0,5 K- błędy powstałe z niedokładności odczytu temperatury

oraz ΔR_t =0.986 i ΔR₂₁ =0.8405 - błędy bezwzględne powstałe z błędu pomiaru. Dla powyższych wartości otrzymujemy błąd bezwzględny pomiaru przerwy równy :

ΔE_g=0,003966≈0,004 [eV]

Ostatecznie przerwa energetyczna półprzewodnika wynosi:

Eg≈0,728±0,004 [eV]

Wnioski:

Pomiar dzięki dość dużej dokładności użytych przyrządów (cyfrowych multimetrów) dość dobrze odtwarza obraz zmian oporności pod wpływem temperatury. Ponieważ przy pomiarze temperatury wystąpiły największe błędy metoda pomiaru temperatury mogła by ulec zmianie. W tym celu należałoby zastąpić zwykły termometr termoparą. Uzyskalibyśmy wtedy przy odpowiednio dokładnej termoparze, błąd pomiaru temperatury przynajmniej o rząd mniejszy od otrzymanego.

Ćwiczenie potwierdza w granicach błędu liniowy związek między temperaturą metalu, a jego rezystancją. Dowiedzieliśmy się też, że wraz ze wzrostem temperatury półprzewodnika rośnie wykładniczo liczba elektronów w paśmie przewodnictwa, a tym samym maleje jego rezystancja. Otrzymany wynik temperaturowego współczynnika rezystancji dla mierzonego przez nas metalu jest zbliżony dla wartości zawartej w tablicach dla platyny (0.0039 [1/K] ).

2

---