WYKŁAD
BAZY DANYCH
Janusz Zyskowski
Łódź 1998/99
Spis Treści
1. Pojęcie bazy danych i systemu zarządzania bazą danych
Pojęcie bazy danych i systemu zarządzania bazą danych
Pojęcia pomocnicze służące do opisu baz danych
Niech X1×X2×...×Xn := { x :=(x1,x2,...,xn) xi ∈ Xi, i=1,2,...,n }. Funkcję zdaniową n - zmiennych określoną na X1×X2×...×Xn oznaczać będziemy przez Φ(x1,x2,...,xn) lub Φ(x).
Definicja. Dla danych zbiorów X1,X2,...,Xn zbiór G ⊆ X1×X2×...×Xn nazywamy relacją n-członową.
Zbiór punktów x ∈ X := X1×X2×...×Xn, dla których funkcja zadaniowa Φ(x1,x2,...,xn) przyjmuje wartość logiczną "prawda" oznaczać będziemy przez { x∈X | Φ(x1,x2,...,xn) } lub { x | (x∈X) ∧ Φ(x1,x2,...,xn) }.
Do geometrycznej ilustracji pewnych pojęć przydatne będzie pojęcie hipergrafu.
Definicja. Hipergrafem (skończonym) nazywamy czwórkę uporządkowaną
H:=( X, K, ω, p),
gdzie
X - skończony zbiór (wierzchołki),
K - skończony zbiór (hiperkrawędzie),
ω : K → X, (ω(k) - początek hiperkrawędzi ),
p : K → ℘(X), ( p(k) koniec hiperkrawędzi ),
(℘(X) oznacza zbiór wszystkich podzbiorów zbioru X ).
Definicja. Niech R:={ R1, R2,..., RN }, KOL:={ α1, α2,..., αM } i H:=( X, K, ω, p) hipergraf. Hipergrafem etykietowanym nazywamy czwórkę uporządkowaną
HE := ( H, A, ϕ, ψ ),
gdzie ϕ : X → R, ψ : K → KOL i A:=(R, KOL). Zbiór A nazywany jest alfabetem etykietującym.
W przypadku, gdy funkcja p : K → ℘(X) redukuje się do funkcji p : K → X to zamiast nazwy hipergraf (etykietowany ) używać będziemy nazwy graf zorientowany (etykietowany ).
Definicja. Graf T:=( X, K, ω, p) nazywamy drzewem zorientowanym, gdy
każdy wierzchołek jest końcem co najwyżej jednej krawędzi;
każdy wierzchołek jest początkiem dowolnej ilości krawędzi;
brak cykli.
Wierzchołek, który nie jest końcem żadnej krawędzi nazywamy korzeniem, a wierzchołek, który nie jest początkiem żadnej krawędzi nazywamy liściem.
Przykład. Niech X:={a,b,c,d,e}, K:={1,2,3,4,5} i funkcje ω : K → X i p : K → ℘(X) dane będą w postaci tabelki
k |
1 |
2 |
3 |
4 |
5 |
ω(k) |
a |
b |
b |
b |
b |
p(k) |
{c,d,e} |
{a} |
{a} |
{c,d} |
{b} |
Hipergraf H:=( X, K, ω, p) można przedstawić graficznie w następujący sposób:
5 b 2
3
4 c
d a
1
e
( Dla uproszczenia rysunków będziemy również używać zamiast ).
Przykład. Niech X:={a,b,c,d,e,f}, K:={1,2,3,4,5} i funkcje ω : K → X i p : K → ℘(X) dane będą w postaci tabelki
k |
1 |
2 |
3 |
4 |
5 |
ω(k) |
a |
a |
b |
b |
e |
p(k) |
b |
e |
c |
d |
f |
a
1 2
b e
3 4 5
c d f
Jest to drzewo zorientowane.
Informacje o sposobie opisu baz danych
Proces przechodzenia od świata rzeczywistego do jego informacyjnej reprezentacji w komputerze nazywać będziemy modelowaniem, a pewien dobrze zdefiniowany sposób jego opisu modelem danych, przy czym sposób zapisania wyselekcjonowanych informacji jaka będzie potrzebna użytkownikowi schematem danych. Pomiędzy informacjami mogą występować relacje (też są informacjami ). Zbiór danych (łącznie z relacjami ) nazywać będziemy bazą danych (BD).
Podstawowe fakty świata rzeczywistego, o których wiedza reprezentowana jest w bazach danych:
występowanie obiektów (entity) - przedmiotów materialnych lub abstrakcyjnych reprezentowanych przez pewne nazwy o których chcemy pamiętać informacje,
pozostawanie tych obiektów we wzajemnych powiązaniach (relationship) między sobą wyrażonych przez n-argumentową funkcję zdaniową (n > 1), której argumentami są nazwy obiektów,
posiadanie przez obiekty wartości atrybutów (value attribute).
Przykład. Przy pomocy jedno argumentowej funkcji zdaniowej Φ określonej na zbiorze obiektów:
Φ(x):="x jest studentem";
Φ(x):= "x jest kobietą",
testujących przynależność obiektu do odpowiedniego zbioru, możemy utworzyć zbiory obiektów: STUDENT, KOBIETA.
Środki sprzętowe i oprogramowanie umożliwiające współpracę z bazą danych nazywamy systemem zarządzania bazą danych, (SZBD).
Funkcje systemu zarządzania bazą danych:
opis danych: logiczny i fizyczny;
możliwości korzystania z bazy;
integralność danych - określenie pewnych warunków, które muszą być spełnione w bazie danych, niezależnie od tego, jakie są w niej aktualnie zapisane wartości;
poufność danych - prawa dostępu poszczególnych użytkowników;
współbieżność dostępu - mechanizmy wykrywające sytuacje konfliktowe w przypadku korzystania jednocześnie z BD przez wielu użytkowników i ich rozwiązywanie;
niezawodność.
Przykłady oprogramowania używanego w SZBD:
1. Oracle, Btrieve, Ingres, Informix, Gupta - (UNIX);
2. Access, dBase, Paradox, Approach, FoxPro, SQL Server - (Windows, Windows 95/NT);
3. dBase, Paradox, FoxPro - (DOS).
Poziomy opisu baz danych:
Poziom wewnętrzny - schemat fizyczny określający sposoby organizacji danych w pamięci zewnętrznej.
Poziom pojęciowy - w procesie modelowania tworzenie przez projektanta bazy danych przy pomocy pewnego języka opisu schematu danych ( DDL - Date Description Language ) i ściśle z nim związanego modelu danych schematu pojęciowego.
Poziom zewnętrzny - sposób widzenia danych przez poszczególnych użytkowników.
W zależności od języka opisu schematu danych ( DDL ) i języka manipulowania danymi ( DML - Data Manipulation Language ) wyróżnia się następujące modele danych:
model hierarchiczny;
model sieciowy;
model relacyjny, (E.F.Cood - 1970);
model zorientowany obiektowo.
W zależności od organizacji systemu bazy danych można dokonać następujących podziałów:
1. ze względu na rozproszenie:
lokalne bazy danych - pamiętanie i udostępnianie danych odbywa się w obrębie jednej instalacji komputerowej;
rozproszone bazy danych - składają się z wielu lokalnych baz danych znajdujących się w różnych instalacjach komputerowych;
2. ze względu na liczbę modeli danych:
jednomodelowe bazy danych - przyjmuje się jeden model danych (np. relacyjny);
wielomodelowe bazy danych - dla jednej bazy danych może współistnieć wiele schematów utworzonych na podstawie różnych modeli danych.
Pojęcie sieciowego modelu danych
Podstawowe typy jednostek danych
W sieciowym modelu danych wyróżnia się następujące jednostki danych:
dana elementarna (date item),
wektor (vector);
grupa powtórzeniowa (repeating group),
rekord (record),
kolekcja (set).
Trzy pierwsze wymienione jednostki mogą istnieć tylko jako składowe rekordu.
Ogólna zasada tworzenia rekordu:
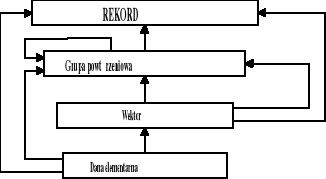
Jeżeli został zdefiniowany typ rekordu R, to możemy mówić o rekordach typu R powstałych po określeniu wartości poszczególnych pól. Jednostki danych definiowane w obrębie jednego typu rekordu mogą pozostawać ze sobą jedynie w powiązaniach hierarchicznych.
Podstawową jednostką dostępu do bazy danych są rekordy. Dostęp do grupy powtórzeniowej, wektora i danej elementarnej jest tylko wtedy gdy udostępniony jest rekord zawierający żądaną jednostkę danych.
Definicja. Skończony zbiór rekordów typu R nazywamy plikiem i zapisujemy następująco:
F(R) := {r1, r2,..., rN},
przy czym z chwilą włączenia rekordu r do pliku F(R) rekord ten może być rozszerzony o jedno pole nazywane kluczem bazy danych (KBD, database key), którego wartość jest jednoznaczna w całej bazie danych i umożliwia jednoznacznie zidentyfikowanie rekordu w tej bazie danych. W przypadku, gdy r∈F(R) będziemy również mówić, że r jest wystąpieniem rekordu typu R.
Przykład. Przykład typu rekordu zapisanego w postaci podobnej do deklaracji rekordu w Pascalu:
PRACOWNIK = Record
nr_pracownika : Integer;
nazwisko : String[20];
data_ur : Array[3] of Integer;
liczba_dzieci : Integer;
dziecko : Array[liczba_dzieci] of Record
imię : String[15];
data_ur : String[8];
End;
liczba_wypłat : Integer;
wypłata : Array[liczba_wypłat] of Real;
End;
Danymi elementarnymi w tym przykładzie są: nr_pracownika, nazwisko, liczba_dzieci, imię, data_ur (w rekordzie dziecko), liczba_wypłat. Dziecko jest grupą powtórzeniową złożoną z dwóch danych elementarnych.
Wystąpienie rekordu tego samego typu można zapisać w postaci tabelarycznej:
nr |
|
data |
liczba |
dziecko |
|
liczba |
|
pracownika |
nazwisko |
urodzenia |
dzieci |
imię |
data_ur |
wypłat |
wypłata |
1234 |
Kowalski |
45 |
2 |
Jan |
79.12.23 |
3 |
234 |
|
|
12 |
|
Anna |
83.11.24 |
|
654 |
|
|
25 |
|
|
|
|
566 |
lub w postaci tzw. drzewa:
PRACOWNIK
1234 Kowalski 2 3
45 12 25 234 654 566
Jan 79.12.23 Anna 83.11.24
Powiązania między rekordami.
Definicja. Niech dane będą dwa typy rekordów R i S i niech XR i XS będą plikami, odpowiednio, typu R i S:
XR := {r1, r2,..., rN},
XS := { s1, s2,..., sM}.
Mówimy, że między rekordami typów R i S istnieje powiązanie, jeśli określone są odwzorowania:
oraz ,
gdzie oznacza zbiór wszystkich podzbiorów zbioru X.
Między rekordami mogą istnieć powiązania sieciowe, tzn. takie, w których jeden rekord może mieć kilka rekordów nadrzędnych (w powiązaniach hierarchicznych może mieć co najwyżej jeden rekord nadrzędny).
W zależności od własności tych odwzorowań wyróżniamy następujące rodzaje powiązań między rekordami typu R i S:
powiązanie jedno-jednoznaczne (1:1) - gdy wartości odwzorowań i są zbiorami jednoelementowymi i co graficznie oznaczamy
R S
powiązanie jedno-wieloznaczne (1:M) - gdy tylko wartość jednego z odwzorowań lub jest zbiorem jednoelementowym i co graficznie oznaczamy
R S lub R S
powiązanie wielo-wieloznaczne (N:M) - gdy odwzorowania i nie spełniają warunków z punktów a) i b) i co graficznie oznaczamy
R S
Przykład. Rozważmy następujące typy rekordów: WYKŁAD, WYKŁADOWCA, KOBIETY, MĘŻCZYŹNI. Między rekordami tych typów można określić między innymi następujące powiązania:
KOBIETY, MĘŻCZYŹNI
być małżeństwem - powiązanie 1 - 1;
być rodzeństwem - powiązanie M - N;
WYKŁAD, WYKŁADOWCA
przypisanie wykładowcy wykładu - powiązanie 1 - M;
Wiele SZBD wymaga usunięcia powiązań wielo-wieloznacznych pomiędzy rekordami. Niech dane będzie powiązanie M:N:
R S
Tworzymy rekord typu T, nazywany rekordem łącznikowym, tak aby uzyskać diagram postaci:
R S
T
Diagram ten nosi nazwę diagramu Bachmana.
Przykład. Rozważmy dwa typy rekordów:
PRACOWNIK( nr, nazwisko ), KURS( nr_kursu, przedmiot )
i dla tego typu rekordów utwórzmy rekord SZKOLENIE( nr, nr_kursu, ocena ). Powiązanie M:N postaci:
PRACOWNIK KURS
możemy zastąpić dwoma powiązaniami typu 1:M:
PRACOWNIK KURS
SZKOLENIE
Daną ocena nazywamy daną powiązań. Nie można jej dołączyć ani do rekordu PRACOWNIK ani do rekordu KURS.
Pojęcie kolekcji.
Definicja. Niech dane będą typy rekordów R, S1, S2, ... ,Sm spełniające następujące warunki:
Si ≠ Sj dla i ≠ j;
dla pewnego i, 1≤ i ≤ m, może zachodzić równość R = Si;
dla każdego i, 1≤ i ≤ m, między rekordami typu R i Si istnieje powiązanie 1:M,
R Si
Wówczas (R,S1,S2,...,Sm) nazywamy typem kolekcji i jeżeli α jest pewną nazwą przyporządkowaną temu typowi kolekcji to używamy również następującego oznaczenia typu kolekcji α(R,S1,S2,...,Sm). Typ rekordu R nazywamy typem właściciela (owner) kolekcji α, a każdy z typów Si typem podwładnego (member) kolekcji α.
Przedstawienie graficzne typu kolekcji α(R,S1,S2,...,Sm) przy pomocy tzw. hiperdrzewa:
R
α
S1 S2 . . . . . . Sm
Przykład.Przykład typu kolekcji pr_dane(PRACOWNIK, PRACA, WYPŁATA, SZKOLENIE, DZIECKO):
PRACOWNIK
pr_dane
PRACA WYPŁATY SZKOLENIE DZIECKO
Uwaga. Z powyższego przykładu widać, że zamiast umieszczać niektóre dane w oddzielnych rekordach można by definiować je jako grupy powtórzeniowe w obrębie rekordu PRACOWNIK. W przypadku potrzebnej informacji o wypłatach nie są potrzebne informacje o dzieciach. Zbędne jest więc sprowadzanie całego rekordu.
Definicja. Typ kolekcji nazywamy jednostkową, gdy jest postaci α(R,S), R≠S i typ rekordu R ma tylko jedno wystąpienie i wystąpienie to jest rekordem pustym.
Definicja. Typ kolekcji nazywamy rekurencyjnym, gdy istnieje i∈{1,2,...,m}, dla którego R=Si.
Przykład. Kolekcją rekurencyjną jest zależność_służbowa( PRACOWNIK, PRACOWNIK ).
Przykłady (typów kolekcji).
R
1) α(R,S,T), β(R,U,V),
α β
S T U V
2) α(S,R,U), β(R,V,W),
S
α
R U
β
V W
3) α(R,R,S,T), (rekurencyjny) ,
R
α
S T
4) α(R,T,U), β(S,U,V), R S
α β
T U V
5) α(R,S,T), β(R,T,U), R
α β
S T U
Definicja. Niech dana będzie kolekcja α(R,S1,S2,...,Sm) i niech r∈F(R) będzie wystąpieniem typu właściciela. Wystąpieniem kolekcji typu α z rekordem właściciela r nazywamy zbiór
α(r):={r,s1,s2,...,sL},
gdzie rekordy s1,s2,...,sL, są różne i pochodzą ze zbioru
F(S1) ∪ F(S2) ∪ ... F(Sm),
( dopuszczalne jest α(r)={r} ).
Zbiór wszystkich wystąpień kolekcji typu α(R,S1,S2,...,Sm) oznaczać będziemy:
KOLEKCJA(α) = {α(r1),α(r2),...,α(rN)},
gdzie F(R) := {r1, r2,..., rN}.
Każdy rekord należący do wystąpienia kolekcji jest rekordem właściciela lub jednego z typów podwładnych.
Uwaga. Ponieważ między typem właściciela i każdym z typów podwładnego w kolekcji α istnieje powiązanie 1:M więc jeden rekord każdego typu podwładnego może należeć co najwyżej do jednego wystąpienia kolekcji α. Do wystąpienia tego może należeć wiele rekordów jednego typu podwładnego lub nie należeć żaden.
W zbiorze wystąpień kolekcji α każde wystąpienie jest jednoznacznie wyznaczone przez wskazanie dowolnego rekordu (właściciela lub podwładnego) należącego do tego wystąpienia.
Sieciowa baza danych.
Bazę danych można traktować jako jednostkę danych.
Definicja. Niech dane będą typy rekordów: R1, R2,..., RN, typy kolekcji: α1, α2,..., αM. Wówczas zbiór
BD(R1, R2,..., RN; α1, α2,..., αM) := { R1, R2,..., RN, α1, α2,..., αM }
nazywamy typem bazy danych.
Definicja. Zbiór
STAN(BD):={ F(R1), F(R2),..., F(RN), kolekcja(α1), kolekcja(α2),...,kolekcja(αM) }
nazywamy stanem bazy danych (wystąpieniem).
Definicja. Niech R:={ R1, R2,..., RN } i KOL:={ α1, α2,..., αM }. Diagramem sieciowego schematu bazy danych nazywamy czwórkę uporządkowaną (hipergrafem etykietowanym)
DSCH:=( H, A, ϕ, ψ ),
gdzie H:=( X, K, ω, p) hipergraf, ϕ : X → R, ψ : K → KOL i A:=(R, KOL) alfabetem etykietującym. W wyniku etykietowania wierzchołkom i krawędziom hipergrafu przypisane są odpowiednio typy rekordów i nazwy kolekcji tworzące alfabet etykietujący.
Przykład. Przykład hipergrafu z § 1.1 użyjemy do utworzenia schematu sieciowej bazy danych. Niech dane będą następujące typy rekordów:
ST:=STUDENT( n_albumu, nazwisko ), PR:=PRACOWNIK( n_pr, nazwisko ),
P:=PRZEDMIOT( n_p, nazwa, n_pr ), SP:=STYPENDIUM( n_albumu,data, wypłata),
EGZ:=EGZAMIN( n_p, n_albumu, ocena), ZAL:=ZALICZENIE( n_p, n_albumu, ocena )
oraz następujące typy kolekcji:
α := α( PR, PR ) - opieka naukowa;
β := β( PR, ST ) - konsultacja pracy dyplomowej;
χ := χ( PR, ST ) - recenzowanie pracy dyplomowej;
δ := δ( ST, EGZ, ZAL, SP ) - przebieg studiów;
η := η( PR, EGZ, ZAL ) - zajęcia dydaktyczne.
Wtedy
typ bazy danych: BD( ST, PR, P, EGZ, ZAL, SP; α, β, γ, δ, η ),
stan bazy danych: STAN(BD)={F(ST),...,F(SP), kolekcja(α), ... ,kolekcja(η) },
diagram schematu bazy danych:
α
β
PR
χ
ST
η
δ
EGZ
ZAL
SP
Prosta sieciowa baza danych (PSBD).
W PSBD przyjmuje się następujące założenia:
jednostki danych: dana elementarna, rekord (tylko z danymi elementarnymi), kolekcja, baza danych;
typy kolekcji: postaci α(R,S);
typ bazy danych definiuje się tak jak w § 2.4.
Uwaga. Diagram schematu bazy danych ma postać hipergrafu etykietowanego, w którym każdy koniec hiperkrawędzi jest zbiorem jednoelementowym. Gdy funkcja p w definicji hipergrafu jest funkcją różnowartościową to mówimy o modelu hierarchicznym a diagram schematu bazy danych nazywamy drzewem rekordów. Założenie 2) nie jest istotnym ograniczeniem, gdyż każdą kolekcję α(R,S1,S2,...,Sm) można przedstawić jako zbiór kolekcji α1(R,S1), α2(R,S2),...,αm(R,Sm).
Przykład.
1) Przykład bazy, która nie jest modelem hierarchicznym: BD(ST,W,P,O; α, β, γ), α(ST,O), β(W,P), γ(P,O),
ST W
α β
O P
2) Przykład bazy, która jest modelem hierarchicznym: BD(W,P,O; β, γ), β(W,P), γ(P,O),
W
β
P
γ
O
Pojęcie relacyjnej bazy danych.
Pojęcie relacji znormalizowanej.
Definicja. Niech dany będzie skończony zbiór U := {A1,A2,...,An}, którego elementy nazywać będziemy atrybutami. Niech każdemu atrybutowi A∈U przyporządkowany będzie zbiór wartości DOM(A) zwany dziedziną atrybutu A, (domeną).
Definicja. Krotką typu U nazywamy dowolną funkcję
![]()
taką, że dla dowolnego A∈U, f(A)∈DOM(A). Zbiór wszystkich krotek typu U oznaczamy przez KROTKA(U).
Uwaga. Zbiór KROTKA(U) może zawierać nieskończenie wiele elementów (krotek) np. gdy jeden ze zbiorów DOM(A) jest zbiorem nieskończonym.
Definicja. Relacją typu U nazywamy dowolny skończony podzbiór zbioru KROTKA(U). Zbiór wszystkich relacji typu U oznaczać będziemy przez REL(U).
Przykład. Niech U := {A1,A2,A3}, gdzie
A1 - część złożona samochodu, DOM(A1):= {samochód,silnik,koło},
A2 - część składowa, DOM(A2):= {podwozie,opona,tłok,koło},
A3 - ilość, DOM(A3):= {1,4,5},
A1 |
A2 |
A3 |
Samochód |
podwozie |
1 |
Samochód |
tłok |
4 |
Samochód |
koło |
5 |
koło |
opona |
1 |
silnik |
tłok |
4 |
Oznaczenia:
Relacje typu U oznaczać będziemy R(U),S(U),T(U),.... Jeżeli z kontekstu wynikać będzie jednoznacznie o jaki zbiór atrybutów chodzi, pisać będziemy R, S, T, ... .
Krotki typu U oznaczać będziemy r(U),s(U),t(U).... Jeżeli z kontekstu wynikać będzie jednoznacznie typ krotki, pisać będziemy r,s,t,....
Podzbiory zbioru atrybutów U oznaczać będziemy dużymi literami X,Y,Z,.... Do oznaczenia sumy dwóch zbiorów X,Y ⊆ U stosować będziemy zapis XY zamiast X∪Y.
Ścisłe przedstawienie krotki utożsamianej ze zbiorem jej wartości wymaga zapisu
r = { (A1, a1), (A2, a2),..., (An, an) }, gdzie ai= r(Ai), i = 1,2,...,n. Zamiast tego będziemy pisać (a1, a2, ... , an).
Dla zbioru atrybutów {A,B} zamiast pisać R({A,B}), stosować będziemy zapis R(A,B).
Uwaga. Niech zbiór U := {A1,A2,...,An}. Ponieważ krotka r(U) jest funkcją więc można ją przedstawić w postaci tabeli:
U |
A1 |
A2 |
... |
An |
r |
r(A1) |
r(A2) |
... |
r(An) |
Gdy R(U) := {r1, r2,..., rm} to można tą relację przedstawić w postaci tabeli:
U |
A1 |
A2 |
... |
An |
|
r1(A1) |
r1(A2) |
... |
r1(An) |
R |
... |
... |
... |
... |
|
rm(A1) |
rm(A2) |
... |
rm(An) |
Definicja. Wartość a∈DOM(A) nazywamy wartością prostą, gdy nie jest ona zbiorem ani ciągiem elementów należących do ![]()
.
Przykład. Niech U := {A1,A2,A3}, DOM(A1) := {{c,d}}, DOM(A2) := {c}, DOM(A3) := {d}, ![]()
= {c,d, {c,d}}. Niech a∈DOM(A1) tzn. a={c,d}. Wartość a nie jest wartością prostą.
Definicja. Mówimy, że relacja R(U) jest relacją znormalizowaną ( pierwszej postaci normalnej -1PN ) gdy dziedziny DOM(A) wszystkich atrybutów A∈U są zbiorami wartości prostych.
Definicja. Dla danej krotki r(U) i X⊂U krotkę t typu X nazywamy ograniczeniem krotki r(U) do zbioru X gdy (∀A∈X) ( r(A)= t(A)}. Dla krotki będącej ograniczeniem będziemy używać oznaczenia r(X) lub r[X].
Przykład. Niech U := {A,B,C}, X := {A,C} i r(U) := (a,b,c). Wtedy r[X] = (a,c).
Operacje na relacjach.
Na relacjach definiuje się pewne operacje mnogościowe i relacyjne.
Definicja. Zbiory
T(U) := { t ∈ KROTKA(U) | t ∈ R(U) ∨ t ∈ S(U) };
T(U) := { t ∈ KROTKA(U) | t ∈ R(U) ∧ t ∉ S(U) };
T(U) := { t ∈ KROTKA(U) | t ∈ R(U) ∧ t ∈ S(U) };
T(U):=KROTKA(U)-R(U) , przy czym zbiór KROTKA(U) jest zbiorem skończonym, gdyż w przeciwnym wypadku byłaby sprzeczność z definicją relacji;
nazywamy odpowiednio sumą, różnicą, przekrojem i dopełnieniem do relacji R(U) i oznaczać będziemy przez R(U)∪S(U), R(U)∩S(U), R(U)-S(U) i -R(U). Zauważmy, że definicje te dotyczą relacji tego samego typu.
Definicja. Niech U będzie zbiorem atrybutów, X,Y⊂U, r∈KROTKA(X), s∈KROTKA(Y) i Z:=X∪Y. Krotkę t∈KROTKA(Z) nazywamy złączeniem krotki r i s, co oznaczamy t=r![]()
s, gdy t[X] = r i t[Y ]= s.
Stwierdzenie. Mają miejsce następujące własności:
r
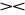
s = s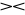
r,r[∅] = ε gdzie ε oznacza krotkę pustą,
r
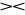
ε = r.
Definicja. Dla danej relacji R(U) oraz zbioru X⊂U relację T(X) nazywamy projekcją R na X, gdy
T = { t ∈ KROTKA(X) | ( ∃ r ∈ R ) ( t = r[X] ) }.
Dla projekcji używać będziemy oznaczenia T=R[X].
Stwierdzenie. Jeżeli dana jest relacja R(U) i X⊂U to
R[X] = { t ∈ KROTKA(X) | ( ∃ s ∈ KROTKA(U-X) ) (t ![]()
s ∈ R ) }.
Przykład. Niech U := {A,B,C} i R(U) określona następująco:
R: |
A |
B |
C |
|
a |
x |
1 |
|
b |
x |
1 |
|
a |
x |
2 |
|
c |
y |
3 |
Dla X:={B,C} mamy:
R [X]: |
B |
C |
|
x |
1 |
|
x |
2 |
|
y |
3 |
Definicja. Odwzorowanie
![]()
przyporządkowujące relacjom typu U ich projekcję na X nazywamy operacją projekcji.
Stwierdzenie. Jeżeli R∈REL(U) to
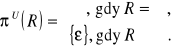
Definicja. Niech U := {A1,A2,...,An}, ![]()
, ⊗∈{ =, ≠, <, >, , }. Elementarnym warunkiem selekcji nazywamy wyrażenia postaci v ⊗ Ai lub Ai ⊗ Aj. Warunkiem selekcji nazywamy:
elementarny warunek selekcji,
wyrażenia postaci: ∼E , E1 ∧ E2 lub E1 ∨ E2 gdzie E , E1, E2 są warunkami selekcji.
Definicja. Relację T(U) nazywamy selekcją relacji R(U) względem warunku selekcji E, co oznaczamy przez T=R/E/, gdy T = {t∈R | E(t)=true }.
Przykład. Dla relacji R(U) postaci
R: |
A |
B |
C |
D |
|
a |
x |
1 |
3 |
|
a |
y |
4 |
2 |
|
c |
x |
3 |
3 |
|
b |
x |
2 |
1 |
z warunkiem selekcji E := ( C D ∧ ( A = a ∨ A = b ) ) relacja T=R/E/ jest postaci
T: |
A |
B |
C |
D |
|
a |
x |
4 |
2 |
|
b |
x |
2 |
1 |
Definicja. Odwzorowanie
![]()
przyporządkowujące relacji typu U jej selekcję względem warunku E nazywamy operacją selekcji.
Definicja. Dla danych relacji R(X) i S(Y) relację
T:={ t ∈ KROTKA(X∪Y) | ( t[X] ∈ R ) ∧ ( t[Y] ∈ S ) }
typu X∪Y nazywamy złączeniem relacji i oznaczamy przez R ![]()
S.
Stwierdzenie. Jeżeli dane są relacje R(X) i S(Y) to
R![]()
S ={ t ∈ KROTKA(X∪Y) | ( ∃ r ∈ R ) ( ∃ s ∈ S ) ( t = r ![]()
s ) }.
Przykład. Dla relacji R(X) i S(Y) określonych następująco:
R: |
A |
B |
C |
|
S: |
A |
B |
D |
|
a |
x |
1 |
|
|
a |
x |
f |
|
a |
x |
2 |
|
|
a |
y |
g |
|
a |
y |
2 |
|
|
b |
x |
h |
|
b |
y |
3 |
|
|
|
|
|
ich złączenie T:=R ![]()
S jest relacją postaci:
T: |
A |
B |
C |
D |
|
a |
x |
1 |
f |
|
a |
x |
2 |
f |
|
a |
y |
2 |
g |
{ krotki nowej relacji tworzone są tylko z tych krotek relacji R i S, które na wspólnych atrybutach mają te same wartości }.
Definicja. Odwzorowanie
![]()
X,Y : REL(X) × REL(Y) → REL(X∪Y)
przyporządkowujące dwóm relacjom typów, odpowiednio X i Y, relację typu X∪Y będącą ich złączeniem nazywamy operacją złączenia.
Stwierdzenie. Dla danych relacji R ,S ,T i X, Y⊂U mamy
R
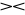
S = S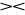
R,(R
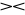
S )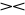
T = R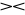
(S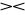
T),jeżeli X⊂U to R[X]
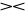
R = R,jeżeli X∪Y=U to R ⊂ R[X]
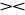
R[Y],jeżeli X=Y to R
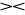
S = R∩S,jeżeli X∩Y=∅ to R
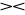
S = R×S.
Przykład. Niech ai ≠ aj, bi ≠ bj, ci ≠ cj, dla i ≠ j, Wtedy dla relacji R określonej następująco:
Ad. 3) U := {A,B}, X := {B}, X∪U = U,
R: |
A |
B |
|
R[X]: |
B |
|
R[X] |
A |
B |
|
a1 |
b1 |
|
|
b1 |
|
|
a1 |
b1 |
|
a1 |
b2 |
|
|
b2 |
|
|
a1 |
b2 |
|
a2 |
b3 |
|
|
b3 |
|
|
a2 |
b3 |
Ad. 5) U := {A,B}, X := {A,B}, Y := {A,B}, X∪Y = {A,B},
R: |
A |
B |
|
S: |
A |
B |
|
R |
A |
B |
|
a1 |
b1 |
|
|
a2 |
b2 |
|
|
a2 |
b2 |
|
a2 |
b2 |
|
|
a3 |
b3 |
|
|
|
|
Ad. 4)
a) U := {A,B,C}, X := {A,B}, Y := {B,C}, X∪Y = {A,B,C},
R: |
A |
B |
C |
|
R[X]: |
A |
B |
|
R[Y]: |
B |
C |
|
R[X] |
A |
B |
C |
|
a1 |
b1 |
c1 |
|
|
a1 |
b1 |
|
|
b1 |
c1 |
|
|
a1 |
b1 |
c1 |
|
a2 |
b2 |
c2 |
|
|
a2 |
b2 |
|
|
b2 |
c2 |
|
|
a1 |
b1 |
c2 |
|
a3 |
b3 |
c3 |
|
|
a3 |
b3 |
|
|
b3 |
c3 |
|
|
a2 |
b2 |
c2 |
|
a1 |
b1 |
c2 |
|
|
|
|
|
|
b1 |
c2 |
|
|
a3 |
b3 |
c3 |
U := {A,B,C}, X := {A}, Y := {B,C}, X∪Y = {A,B,C},
R[X]: |
A |
|
R[Y]: |
B |
C |
|
R[X] |
A |
B |
C |
|
a1 |
|
|
b1 |
c1 |
|
|
a1 |
b1 |
c1 |
|
a2 |
|
|
b2 |
c2 |
|
|
a1 |
b2 |
c2 |
|
a3 |
|
|
b3 |
c3 |
|
|
a1 |
b3 |
c3 |
|
|
|
|
b1 |
c2 |
|
|
a2 |
b1 |
c1 |
|
|
|
|
|
|
|
|
a2 |
b2 |
c2 |
|
|
|
|
|
|
|
|
... |
... |
... |
|
|
|
|
|
|
|
|
a3 |
b3 |
c3 |
Ad. 6) X := {A}, Y := {B}, X∪Y = {A,B},
R: |
A |
|
S: |
B |
|
R |
A |
B |
|
a1 |
|
|
b2 |
|
|
a1 |
b2 |
|
a2 |
|
|
b3 |
|
|
a2 |
b2 |
|
|
|
|
|
|
|
a1 |
b3 |
|
|
|
|
|
|
|
a2 |
b3 |
Definicja. Dla danej relacji R(U) i zbioru X⊂U relację T(U-X) nazywamy podzieleniem relacji R przez zbiór X, co oznaczamy przez T=R/X, gdy
T={ t ∈ KROTKA(U-X) | ( ∀ s ∈ KROTKA(X) ) ( t![]()
s ∈ R ) },
{ krotka t typu U-X należy do R/X, gdy dla każdej krotki s typu X złączenie krotek t i s jest krotką należącą do R}.
Przykład. Niech U:={A,B), X:={B}, U-X = {A} zbiory DOM(A):={1,2,3}, DOM(B):={a,b,c}. Wtedy T:=R/{B} dla relacja R(U) określonej następująco:
R: |
A |
B |
|
|
T: |
A |
|
1 |
a |
|
|
|
1 |
|
2 |
b |
|
|
|
|
|
1 |
b |
|
|
|
|
|
1 |
c |
|
|
|
|
|
3 |
c |
|
|
|
|
Niech 1,2,3 oznacza numer studenta i a,b,c nazwę przedmiotu. Niech (n,p) ∈ R(U) oznacza, że student n zdał egzamin z przedmiotu p. Zatem n∈T, gdy student n zdał wszystkie egzaminy.
Definicja. Odwzorowanie
![]()
które relacji typu U przyporządkowuje relację będącą wynikiem podzielenia przez zbiór X nazywamy operacją dzielenia.
Twierdzenie. Jeżeli dana jest relacja R(U), X⊂U i KROTKA(U) jest zbiorem skończonym to
R/X = -(-R )[-X ], ![]()
gdzie " - " oznacza operację dopełnienia tzn. -X := U-X, -R(U) := KROTKA(U)-R(U).
Dowód. Ponieważ
(-R)[-X] = { t∈KROTKA(U-X) | (∃s∈KROTKA(X)) (t![]()
s ∈ (-R) ) }
i prawdą jest, że jeżeli A={ t | Φ(x) } to -A={ t | ∼Φ(x) }, więc
-(-R)[-X] = { t∈KROTKA(U-X) | ∼ (∃s∈KROTKA(X)) (t![]()
s ∈ (-R) ) }=
{ t ∈ KROTKA(U-X) | (∀ s ∈ KROTKA(X) ) (t![]()
s ∈ R ) } = R/X .
ÿ
Definicja. Dla danych relacji R(U) i S(X), X⊂U relację T(U-X) nazywamy podzieleniem relacji R przez relację S, co oznaczamy przez T = R:S, gdy
T = { t ∈ R [U-X] | ( ∀ s ∈ S ) (t![]()
s ∈ R ) }.
Stwierdzenie. Dla relacji R(U), S(X), X⊂U
R:S = { t ∈ R [U-X] | ( S ⊂ R(t,X) ) },
gdzie
R(t,X) := { s ∈ R[X] | (t![]()
s ∈ R ) }.
Dowód. Wystarczy wykazać, że ( ∀ s ∈ S ) (t![]()
s ∈ R ) ⇔ S ⊂ R(t,X) ). Przypuśćmy, że jest prawdziwa lewa strona równoważności i prawa fałszywa. Wtedy (∃s∈S) (s∉R(t,X)) tzn. t![]()
s∉R, co jest sprzeczne z założeniem. Przypuśćmy teraz, że prawdziwa jest prawa strona i lewa fałszywa. Wtedy (∃s∈S) (t![]()
s ∉ R ) tzn. s ∉ R(t,X), co jest sprzeczne z założeniem o prawdziwości prawej strony.
ÿ
Przykład. Niech U := {A,B}, X := {B }, U-X = {A} oraz
R: |
A |
B |
|
|
S: |
B |
|
T=R:S : |
A |
|
1 |
a |
|
|
|
a |
|
|
1 |
|
2 |
b |
i |
|
|
b |
.Wtedy |
|
|
|
1 |
b |
|
|
|
c |
|
|
|
|
1 |
c |
|
|
|
|
|
|
|
|
3 |
c |
|
|
|
|
|
|
|
{ Różnica między R/X i R:S polega na tym, że w przypadku R/X mówimy o wszystkich "wartościach" atrybutu B a w przypadku R:S o "wartościach" atrybutu B o których informacje zawarte są w relacji S}.
Uwaga. Ostatnie stwierdzenie daje możliwość stworzenia pewnego algorytmu wyznaczania relacji T(U-X) := R(U):S(X).
Uwaga. Operacje mnogościowe i relacyjne zdefiniowane w 3.2 tworzą zbiór operacji algebry relacji. Operacje te wykorzystuje się do
tworzenia języków manipulowania danymi;
badania zależności między danymi;
projektowania schematu logicznego relacyjnych baz danych.
Zależności funkcyjne.
Definicja. Niech U będzie zbiorem atrybutów i X,Y⊂U. Mówimy, że istnieje zależność funkcyjna między zbiorami X i Y, co oznaczamy X→Y, gdy w każdej relacji R(U) ⊂ KROTKA(U) istnieje pewna funkcja R[X]→ R[Y], (przy różnych relacjach R(U) funkcje te mogą być różne). Gdy X = { A1, A2..., An } i Y = { B1, B2..., Bm }, gdzie Ai, Bi oznaczają pojedyńcze atrybuty z U, to będziemy również używać oznaczenia A1A2...An→B1B2...Bm.
Definicja. Dla danej relacji R(U), X,Y⊂U, mówimy że w R spełniona jest zależność funkcyjna X→Y, gdy
(∗) (∀ r1,r2 ∈ R ) [ ( r1(X)=r2(X) ) ⇒ ( r1(Y)=r2(Y) ) ].
Przykład. Niech U := {nr_Indeksu,Nazwisko_studenta,nr_Przedmiotu,Ocena} i relacja R(U) określona następująco:
R: |
I |
N |
P |
O |
|
1 |
a |
101 |
3 |
|
1 |
a |
102 |
4 |
|
2 |
b |
101 |
3 |
|
3 |
c |
101 |
3 |
W relacji R(U) spełnione są następujące zależności funkcyjne: I→N , IP→O. Zauważmy, że dla zbiorów {P} i {O} warunek z (∗) jest również spełniony, ale między tymi zbiorami nie istnieje zależność funkcyjna. Istotnie, po dodaniu krotki (3, c, 102, 3) warunek z (∗) nie będzie spełniony.
Definicja, ( założenie o relacji uniwersalnej ). Dla danego zbioru atrybutów U istnieje jedna relacja R(U), a wszystkie inne relacje typu X, X⊂U uzyskuje się z R w wyniku operacji projekcji. Relację R nazywamy relacją uniwersalną.
Uwaga. Przyjęcie założenia o relacji uniwersalnej pozwala mówić o istnieniu uniwersalnego zbioru zależności funkcyjnych na zbiorze U. W dalszej części będziemy przyjmowali, że zbiór U spełnia założenie o relacji uniwersalnej.
Aksjomaty Armstronga.
Przykład. Niech U:={Przedmiot, nr_Indeksu, Ocena,nr_Egzaminatora, Godzina_egzaminu, Sala}. Na tym zbiorze atrybutów można określić np. następujący zbiór zależności funkcyjnych:
F := { P→GS, GS→P, PI→O, GI→PS, PGS→E }.
Zamiast zależności funkcyjnej P→GS można wprowadzić dwie zależności P→G i P→S. Poza tym np. z zależności P→GS wynika zależność PE→GS.
Problem. Czy można rozpatrywać zależności funkcyjne ( w tym wyprowadzanie nowych ) bez odwoływania się do relacji ? (Odpowiedzi udzielił Armstrong).
Aksjomaty Armstronga. Niech U będzie zbiorem atrybutów i niech
F ⊂ { X → Y | ( X ⊂ U ) ∧ ( Y ⊂ U ) }.
Przez F+ oznaczmy najmniejszy (ze względu na relację zawierania) zbiór zależności funkcyjnych, który zawiera zbiór F i dla dowolnych X,Y,Z⊂U spełnia następujące aksjomaty:
( Y ⊂ X ) ⇒ [ (X → Y ) ∈ F+ ], (zwrotność);
[ (X → Y ) ∈ F+ ] ⇒ [ (XZ → YZ ) ∈ F+ ], (poszerzalność);
[ (X → Y ) ∈ F+ ∧ (Y → Z ) ∈ F+] ⇒ [ (X → Z ) ∈ F+ ], (przechodniość).
Zbiór F+ nazywamy najmniejszym domknięciem zbioru F.
Twierdzenie. Układ aksjomatów Armstronga jest niesprzeczny, tzn., że istnieje relacja typu U w której aksjomaty F1-F3 są prawdziwe.
Dowód. Pokażemy, że relacją tą jest dowolna relacja typu U. Twierdzenie będzie udowodnione, jeżeli pokażemy, że każda zależność funkcyjna (X → Y ) ∈ F+ jest spełniona w każdej relacji typu U, w której spełnione są wszystkie zależności funkcyjne ze zbioru F.
Ad. F1). Nie może istnieć relacja R(U), dla której przy Y⊂X istnieją r1,r2∈R takie, że (r1(X)=r2(X)) ∧ (r1(Y)≠r2(Y)).
Ad. F2). Przypuśćmy, że istnieje relacja R(U), w której spełniona jest zależność funkcyjna X→Y i istnieje Z, takie że nie jest spełniona zależność funkcyjna XZ→YZ. Wtedy istnieją dwie krotki r1,r2∈R, dla których
( r1(XZ) = r2(XZ) ) ∧ ( r1(YZ) ≠ r2(YZ) ).
Skąd wynika, że
(r1(Z) = r2(Z)) ∧ (r1(X) = r2(X)) ∧ (r1(Y) ≠ r2(Y)),
co jest sprzeczne z faktem, że w R(U) spełniona jest zależność funkcyjna X→Y.
Ad. F3). Niech zależności funkcyjne X→Y i Y→Z będą spełnione w R(U). Korzystając z prawa ((p⇒q)∧(q⇒r)) ⇒ (p⇒q) do zdania
[ ( r1(X)=r2(X) ) ⇒ ( r1(Y)=r2(Y) )] ∧ [ ( r1(Y)=r2(Y) ) ⇒ ( r1(Z)=r2(Z) ) ]
otrzymamy ( r1(X)=r2(X) ) ⇒ ( r1(Y)=r2(Y) ) co oznacza, że w R(U) spełniona jest zależność funkcyjna X→Z.
ÿ
Twierdzenie. Niech F będzie zbiorem zależności funkcyjnych określonych na U i niech X,Y⊂U. Zależność funkcyjna X→Y należy do F+ wtedy i tylko wtedy, gdy
Y⊂ X+:= { A ∈ U | (X → A ) ∈ F+ }.
( Zbiór X+ nazywamy domknięciem zbioru X względem zbioru F ).
Dowód. 1) Niech Y⊂X+ tzn. Y:={A1,A2,..., Ak) i (∀i) [(X→Ai )∈F+]. Z aksjomatów F2 i F3 wynika prawdziwość implikacji
[ (X → Z ) ∈ F+ ∧ (X → Y ) ∈ F+] ⇒ [ (X → YZ ) ∈ F+ ].
Istotnie
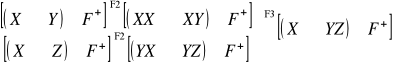
.
Zatem
[ ( X → A1 ) ∈ F+ ∧ ( X → A2 ) ∈ F+ ] ⇒ [ ( X → A1 A2 ) ∈ F+ ],
[ ( X → A1 A2 ) ∈ F+ ∧ ( X → A3 ) ∈ F+ ] ⇒ [ ( X → A1 A2 A3 ) ∈ F+ ],
........................................................................................
[ ( X → A1 A2 ...Ak-1 ) ∈ F+ ∧ ( X → Ak ) ∈ F+ ] ⇒ [ ( X → A1 A2 ...Ak-1Ak ) ∈ F+ ],
co oznacza, że ( X→Y )∈F+.
2) Niech (X→Y)∈F+ i niech Y:={A1,A2,..., Ak). Dla dowolnego atrybutu Ai∈Y z aksjomatu F1 wynika, że (Y→Ai)∈F+. Z aksjomatu F3 otrzymamy
[ ( X → Y ) ∈ F+ ∧ ( Y → Ai ) ∈ F+ ]⇒ [ ( X → Ai ) ∈ F+ ].
Wobec dowolności wyboru Ai mamy, że (∀Ai) [(X→Ai)∈F+] tzn. Y⊂X+.
ÿ
Twierdzenie. Jeżeli dla danego zbioru zależności funkcyjnych F zależność X→Y nie należy do F+ to istnieje relacja R(U), w której spełnione są wszystkie zależności funkcyjne ze zbioru F+ i nie jest spełniona zależność X→Y.
Dowód. Niech F będzie zbiorem zależności funkcyjnych określonych na U i niech (X→Y)∉F+, X,Y⊂U.
Rozważmy relację
R: |
|
|
X+ |
|
|
|
|
U-X+ |
|
|
|
1 |
1 |
... |
1 |
1 |
1 |
1 |
... |
1 |
1 |
|
1 |
1 |
... |
1 |
1 |
0 |
0 |
... |
0 |
0 |
Pokażemy, że wszystkie zależności z F+ są spełnione w R. Przypuśćmy, że (V→W)∈F+ i nie jest spełniona w R. Jest to możliwe tylko wtedy gdy V⊂X+ i jednocześnie W⊄X+. Ponieważ V⊂X+, więc na podstawie poprzedniego twierdzenia (X→V)∈F+. Ponieważ z założenia (V→W)∈F+, więc na podstawie aksjomatu F3, (X→W)∈F+. Zatem, ponownie korzystając z poprzedniego twierdzenia, W⊂X+, co jest sprzeczne z założeniem, że W⊄X+. Wykazaliśmy więc, że jeżeli (V→W)∈F+ to jest ona spełniona w R.
Wykażemy teraz, że jeżeli (X→Y)∉F+ to zależność X→Y nie jest spełniona w R. Przypuśćmy, że X→Y jest spełniona w R. Zatem Y⊂X+ i z poprzedniego twierdzenia otrzymamy, że (X→Y)∈F+, co jest sprzeczne z założeniem.
ÿ
Stwierdzenie, (wynikające z aksjomatów Armstronga).
[ (X → Y ) ∈ F+ ∧ (YW → Z ) ∈ F+] ⇒ [ (XW → Z ) ∈ F+ ],
[ (X → Y ) ∈ F+ ∧ (X → Z ) ∈ F+] ⇒ [ (X → YZ ) ∈ F+ ],
[ (X → YZ ) ∈ F+ ] ⇒ [ (X → Y ) ∈ F+ ∧ (X → Z ) ∈ F+ ].
Definicja. Niech dany będzie zbiór zależności funkcyjnych F określonych na U. Najmniejszy podzbiór F0 zbioru F+, ( F0⊂F+ ), taki że F0+=F+ nazywamy minimalnym generatorem zbioru F+. Jeżeli ponadto wszystkie zależności (X→Y) ∈ F0 są takie, że X jest możliwie najmniejszym podzbiorem U, a Y pojedyńczym atrybutem należącym do U, to F0 nazywamy minimalnym zredukowanym generatorem zbioru F+.
Przykład. Niech U := { P,I,O,E,G,S } i F := { P→GS, GS→P, PI→O, GI→PS, PGS→E }. Przykładami minimalnych zredukowanych generatorów całego zbioru F+ są:
F01 := { P → G, P → S, GS → P, PI → O, GI → P, P → E },
F02 := { P → G, P → S, GS → P, PI → O, GI → S, P → E }.
Uwaga. Zredukowane generatory nie muszą być wyznaczone jednoznacznie.
Zadanie. Dla zbior*w U := { A, B, C } i F := { AC→B, B→C } wyznaczyć zbi*r F+ i minimalne generatory zbioru F+.
Schemat relacyjny i jego związek z relacją.
Definicja. Niech dla danego zbioru atrybutów U F będzie zbiorem zależności funkcyjnych określonych na U. Parę uporządkowaną
R:=( U, F )
nazywamy schematem relacyjnym o zbiorze atrybutów U i ze zbiorem zależności F.
Definicja. Mówimy, że relacja R jest przypadkiem schematu relacyjnego R:=(U,F), (lub, że jej schematem jest R ), gdy R jest relacją typu U i spełniona jest w niej każda zależność funkcyjna (X→Y)∈F. Zbiór wszystkich relacji R o schemacie R oznaczać będziemy przez INST(R).
Definicja. Dla danego schematu relacyjnego R:=(U,F) i X⊂U schemat relacyjny Π:=(X,G) nazywamy projekcją schematu R na zbiór X, co oznaczamy przez Π=R[X], gdy
G+ = { (Y → Z ) ∈ F+ | Y ∪ Z ⊂ X }+,
tzn. G jest podzbiorem zbioru tych zależności ze zbioru F+, w których występują tylko atrybuty ze zbioru X.
Przykład. Dla R:=({P,I,O,E,G,S}, {P→GSE, GS→P, PI→O, GI→P}) mamy R[{I,O,G,S }]:= ({I, O, G, S},{IGS→O}). Zauważmy, że gdyby w definicji zbioru G+ nie było domknięcia F+ to otrzymalibyśmy zbiór pusty.
Definicja. Dla schematów relacyjnych R:=(X,F) i S:=(Y,G) schemat Π:=(Z,H) nazywamy złączeniem schematów R i S, co oznaczamy przez Π=R![]()
S, gdy Z=X∪Y i H=F∪G.
Rozkładalność schematów relacyjnych.
Definicja. Mówimy, że schemat relacyjny R:=(U,F) jest rozkładalny bez straty danych na dwa schematy R[X] i R[Y], gdy
X ∪ Y = U,
(∀ R ∈ INST(R ) ) ( R = R[X]
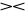
R[Y] ).
Twierdzenie. Schemat relacyjny R:=(U,F) jest rozkładalny bez straty danych na schematy R[XY] i R[XZ], XYZ=U, Y∩Z=∅ wtedy i tylko wtedy, gdy (X→Y)∈F+ lub (X→Z)∈F+ tzn., gdy dla każdej relacji R o schemacie R:=(U,F) mamy
( R=R[XY]![]()
R[XZ] ) ⇔ [ (X→Y)∈F+ ∨ (X→Z)∈F+ ].
{ Warunek wystarczający można udowodnić jeżeli (X→Y)∈F+ lub (X→Z)∈F+ zastąpimy (X→Y)∈F }.
Przykład. Relacja EGZ(U), U:={I, N, P, O}, gdzie
EGZ: |
I |
N |
P |
O |
|
10 |
f |
a |
3 |
|
10 |
f |
b |
4 |
|
11 |
g |
a |
3 |
|
12 |
h |
a |
3 |
jest przypadkiem schematu relacyjnego E:=( {I, N, P, O}, {I→N, IP→O} ). W zależności od wyboru zbioru zależności funkcyjnych jako podstawy rozkładu relację tą można rozłożyć bez straty danych na dwa sposoby:
a)
E1: |
I |
N |
|
E2: |
I |
P |
O |
|
10 |
f |
|
|
10 |
a |
3 |
|
11 |
g |
|
|
10 |
b |
4 |
|
12 |
h |
|
|
11 |
a |
3 |
|
|
|
|
|
12 |
a |
3 |
b)
E3: |
I |
P |
O |
|
E4: |
I |
P |
N |
|
10 |
a |
3 |
|
|
10 |
a |
f |
|
10 |
b |
4 |
|
|
10 |
b |
f |
|
11 |
a |
3 |
|
|
11 |
a |
g |
|
12 |
a |
3 |
|
|
12 |
a |
h |
W obydwu przypadkach mamy: EGZ=E1![]()
E2, EGZ=E3![]()
E4.
Definicja. Mówimy, że schemat relacyjny R:=(U,F) jest rozkładalny bez straty zależności na dwa schematy R1:=(X,G), R2:=(Y,H), gdy
X ∪ Y = U,
F+ = ( G ∪ H )+.
Przykład. Dla schematu relacyjnego
R := ( { A, B, C, D }, { A → B , BC → D , D → B , D → C } ) = ( U, F )
rozważmy następujące schematy:
R1 := ( { A, B }, { A → B } ), R2 := ( { B, C, D }, { BC → D , D → B , D → C } ),
będące rozkładami schematu R bez straty zależności. Rozkład ten nie jest jednak rozkładem bez straty danych. Istotnie, rozważmy relację R∈INST(R) postaci:
R: |
A |
B |
C |
D |
|
a |
b |
c |
d |
|
a1 |
b |
c1 |
d1 |
|
a2 |
b |
c1 |
d1 |
Wówczas relacje R1:=R[AB] i R2:=R[BCD] mają postać:
R1: |
A |
B |
|
R2: |
B |
C |
D |
|
a |
b |
|
|
b |
c |
d |
|
a1 |
b |
|
|
b |
c1 |
d1 |
|
a2 |
b |
|
|
|
|
|
i R≠R1![]()
R2. Zauważmy, że zależności B→A i B→CD nie należą do F+, tzn. nie są spełnione założenia twierdzenia o warunku koniecznym i dostatecznym rozkładalności bez straty danych.
Sposób rozkładu bez straty danych i bez straty zależności podaje następna definicja.
Definicja. Mówimy, że schemat relacyjny R:=(U,F) jest rozkładalny na dwie składowe niezależne S:=(X,G) i T: = (Y,H), gdy
X ∪ Y = U,
F+ = ( G ∪ H )+,
(∀ R ∈ INST(R) ) ( R = R[X]
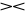
R[Y] ).
Twierdzenie. Schemat relacyjny R:=(U,F) jest rozkładalny na dwie składowe niezależne S[X]:=(X,G) i T[Y]:=(Y,H), X,Y⊂U, X∪Y=U, X∩Y≠∅, wtedy i tylko wtedy, gdy:
F+ = ( G ∪ H )+,
[( X ∩ Y → X ) ∈ F+ ] ∨ [ ( X ∩ Y → Y ) ∈ F+ ].
Normalizacja schematów relacyjnych do drugiej postaci normalnej (2PN).
Definicja. Mówimy, że zbiór K⊂U jest kluczem dla schematu relacyjnego R:=(U,F), gdy spełnia warunki:
( K → U ) ∈ F+,
(∀ X ⊂ U ) ( [ ( X → U ) ∈ F+ ] ⇒ [ ∼ ( X ⊂ K ) ] ).
Elementy zbioru K nazywamy atrybutami kluczowymi.
Przykład. Dla schematu relacyjnego E:=( {I, N, P, O}, {I→N, IP→O} ) warunek a) definicji spełniają zbiory {I, P}, {I, N, P}, {I, N, P, O}. Warunek b) spełnia zbiór {I, P} i ten zbiór jest kluczem schematu R.
Uwaga. Schemat relacyjny może posiadać wiele kluczy. Jeden z nich nazywamy kluczem głównym, (primary key).
Definicja. Niech X,Y⊂U i X∩Y=∅. Mówimy, że Y jest w pełni funkcyjnie zależny od X, gdy istnieje zależność funkcyjna X→Y i nie istnieje zależność z żadnego podzbioru właściwego zbioru X w Y.
Definicja. Schemat relacyjny R := (U,F) jest w drugiej postaci normalnej (2PN), gdy każdy niekluczowy atrybut A∈U jest w pełni zależny od każdego klucza tego schematu.
Przykład. Schemat relacyjny E:=( {Indeks, Nazwisko, Kierunek, Adres, Przedmiot, Ocena}, {I→NAK, IP→O }) z kluczem K:={I, P} nie jest w 2PN, bo np. niekluczowy atrybut N jest zależny funkcyjnie tylko od { I } ⊂ K. Niech E będzie relacją o schemacie E określoną następująco:
E: |
I |
N |
A |
K |
P |
O |
|
10 |
f |
x |
mat |
a |
3 |
|
10 |
f |
x |
mat |
b |
4 |
|
11 |
g |
y |
inf |
a |
3 |
|
12 |
h |
x |
inf |
a |
3 |
|
10 |
f |
x |
mat |
c |
5 |
W relacji tej można zauważyć następujące anomalia:
dołączania - nie można dołączyć studenta, który nie zdał żadnego egzaminu;
aktualizacji - zmiana adresu studenta wymaga zmiany w kilku krotkach;
usuwania - np. przy unieważnieniu egzaminu studenta o indeksie 11 należy usunąć całą krotkę, co spowoduje utratę informacji o studencie.
Dla każdej relacji E∈INST(E) mamy E=E[INKA]![]()
E[IPO] tzn. uzyskaliśmy dwa schematy relacyjne E1:=({I, N, K, A}, {I→NAK}) i E2:=({I, P, O}, {IP→O}) odpowiednio z kluczami {I} i {I,P}. Jest to rozkład bez straty danych. Relację E można zastąpić dwiema relacjami:
E1: |
I |
N |
A |
K |
|
E2: |
I |
P |
O |
|
10 |
f |
x |
mat |
|
|
10 |
a |
3 |
|
11 |
g |
y |
inf |
|
|
10 |
b |
4 |
|
12 |
h |
x |
inf |
|
|
11 |
a |
3 |
|
|
|
|
|
|
|
12 |
a |
3 |
|
|
|
|
|
|
|
10 |
c |
5 |
Każdy z tych rozkładów jest w 2PN.
Stwierdzenie. Jeżeli każdy klucz schematu jest zbiorem jednoelementowym to schemat jest w 2PN.
Normalizacja schematów relacyjnych do trzeciej postaci normalnej (3PN).
Definicja. Zbiór atrybutów Z jest tranzytywnie zależny od zbioru X, gdy
X ∩ Z = ∅,
(∃Y ⊂ U) { (Y∩X = ∅ ∧ Y∩Z = ∅) ⇒ [ (X→Y )∈F+ ∧ (Y→X)∉F+ ∧ (Y→Z)∈F+] }.
|
|
Y |
|
Z |
(X→Y )∈F+ ∧ (Y→X)∉F+ (Y→Z)∈F+
Definicja. Schemat relacyjny R:=(U,F) jest w trzeciej postaci normalnej (3PN), gdy jest w 2PN i każdy zbiór niekluczowych atrybutów Z⊂U nie jest tranzytywnie zależny od każdego zbioru atrybutów X będącego kluczem tego schematu.
Przykład. Schemat relacyjny E:=({Wykonawca,Adres,Projekt,Data_zakończenia}, {W→APD, P→D}) z kluczem K:={W} jest w 2PN. Niech E będzie relacją o schemacie E określoną następująco:
E: |
W |
A |
P |
D |
|
30 |
x |
a |
f |
|
40 |
y |
a |
f |
|
50 |
y |
b |
g |
|
60 |
z |
c |
f |
Ponieważ W → P ∧ P → D to W → D tzn. zbiór {D} jest tranzytywnie zależny od zbioru {W}. W relacji tej można zauważyć następujące anomalia: dołączania, aktualizacji i usuwania. Dla każdej relacji E∈INST(E) mamy E=E[WAP]![]()
E[PD] tzn. uzyskamy dwa schematy relacyjne E1:=( {W, A, P}, {W→A, W→P} ) i E2:=( { P, D}, {P→D} ), przy czym każdy z nich jest 3PN. Jest to rozkład bez straty danych. Relację E można zastąpić dwiema relacjami:
E1: |
W |
A |
P |
|
E2: |
P |
D |
|
30 |
x |
a |
|
|
a |
f |
|
40 |
y |
a |
|
|
b |
g |
|
50 |
y |
b |
|
|
c |
f |
|
60 |
z |
c |
|
|
|
|
Uwaga. W każdym schemacie będącym w 3PN między atrybutami niekluczowymi nie ma zależności funkcyjnych.
Zadanie. Sprawdzić, czy schemat relacyjny E:=( {A, B, C}, {AB→C, C→A} ) jest w 3PN.
Normalizacja schematów relacyjnych do postaci normalnej Boyce'a-Codda (PNB-C).
Definicja. Schemat relacyjny R:=(U,F) jest w postaci normalnej Boyce'a-Codda, (PNB-C), gdy z istnienia zależności funkcyjnej (X→Y )∈F+, Y ⊂ U-X, wynika, że (X→U )∈F+.
Uwaga. Każdy schemat w PNB-C jest w 3PN.
Przykład. Schemat relacyjny E:=( {Student, Przedmiot, Wykładowca}, {W→P, SP→W} ) z kluczem K:={S,P} nie jest w PNB-C, bo mimo, że W→P ∈F+, to nie istnieje zależność W→U.
Niech E będzie relacją o schemacie E określoną następująco:
E: |
S |
P |
W |
|
10 |
a |
x |
|
11 |
a |
x |
|
10 |
b |
y |
|
11 |
b |
z |
W relacji E występują anomalia usuwania i dołączania. Nie można dołączyć wykładowcy i przedmiotu jeżeli brak chociaż jednego studenta uczęszczającego na wykład. Nie można również usunąć ostatniego studenta uczęszczającego na dany przedmiot.
Schemat E można rozłożyć na dwa schematy relacyjne E1:=( {W, P}, {W→P} ) i E2:=( { W, S}, ∅), z których każdy jest w PNB-C. Wtedy relację E można przedstawić w postaci:
E1: |
W |
P |
|
E2: |
W |
S |
|
x |
a |
|
|
x |
10 |
|
y |
b |
|
|
x |
11 |
|
z |
b |
|
|
y |
10 |
|
|
|
|
|
z |
11 |
Ponieważ ![]()
, więc rozkład ten jest rozkładem bez straty danych, ale nie jest rozkładem bez straty zależności, bowiem {W→P, SP→W}+ ≠ {{W→P} ∪ ∅ }+. Nie jest możliwe dopisanie krotki (z,10) do relacji E2, bowiem wykładowca z prowadzi wykład z przedmiotu b, a student 10 uczęszcza na ten przedmiot do wykładowcy y.
Zależności wielowartościowe.
Definicja. Niech X,Y⊂U, Z := U - XY. Mówimy, że istnieje zależność wielowartościowa między zbiorami X i Y, co oznaczamy przez X →>Y, gdy dla każdego zbioru KROTKA(U) istnieje pewna funkcja ω : KROTKA(X)→℘(KROTKA(YZ)), gdzie ℘(KROTKA(YZ)) oznacza zbiór wszystkich podzbiorów zbioru KROTKA(YZ), taka, że jeżeli do zbioru ω( KROTKA(X)) należą krotki ( y, z ) i (y′, z′ ), to należą również krotki ( y′, z ) i (y, z′ ).
Definicja. Niech dana będzie relacja R(U), X, Y ⊂ U i Z := U - XY. Mówimy, że w R spełniona jest zależność wielowartościowa X →> Y, gdy spełniony jest jeden z równoważnych warunków:
![]()
Uwaga. Każda zależność funkcyjna jest zależnością wielowartościową.
Uwaga. Zależności X →> U i X →> ∅ spełnione są w każdej relacji R(U). Nazywamy je trywialnymi zależnościami wielowartościowymi.
Przykład.
a) |
E: |
P |
D |
Z |
R |
P →> D |
|
|
a |
x |
10 |
1983 |
P →> ZR |
|
|
a |
y |
10 |
1983 |
|
|
|
a |
x |
15 |
1984 |
|
|
|
a |
y |
15 |
1984 |
|
|
|
b |
z |
12 |
1983 |
|
|
|
b |
z |
16 |
1984 |
|
b) |
E1: |
P |
D |
|
E2: |
P |
Z |
R |
|
|
a |
x |
|
|
a |
10 |
1983 |
|
|
a |
y |
|
|
a |
15 |
1984 |
|
|
b |
z |
|
|
b |
12 |
1983 |
|
|
|
|
|
|
b |
16 |
1984 |
P →> D P →> ZR .
Aksjomaty zależności wielowartościowych.
Definicja. Niech U będzie zbiorem atrybutów i M ⊂ { X →> Y | X ⊂ U ∧ Y ⊂ U }. Przez oznaczmy najmniejszy (ze względu na relację zawierania ) zbiór zależności wielowartościowych takich, że M ⊂ i dla spełnione są następujące aksjomaty:
M0. ( zwrotność ),
M1. ( dopełnialność ),
M2. ( poszerzalność ),
M3. ( przechodniość ),
M4. ( pseudo-przechodniość ),
M5. ( addytywność ),
M6. ( dekompozycja ).
Uwaga. Między zależnościami funkcyjnymi i wielowartościowymi zachodzą następujące związki:
FM1.
FM2.
Definicja. Dla zbioru atrybutów U i zbiorów F i M, ( zakładamy, że zbiór M nie zawiera zależności funkcyjnych), parę
R := ( U, F ∪ M )
nazywamy schematem relacyjnym i mówimy, że relacja R jest przypadkiem schematu relacyjnego R jeśli jest relacją typu U oraz każda zależność funkcyjna i wielowartościowa jest spełniona w R.
Czwarta postać normalna, (4PN).
Definicja. Mówimy, że schemat relacyjny R := ( U, F ∪ M ) jest w 4PN gdy
Przykład. Dla schematu relacyjnego
R := ( { P, D, Z, R }, {D → P, PR → Z, P →> D, })
i relacji E z przykładu z * 3.10 rozważmy dwa schematy
R1 := ( { P, D }, {D → P }), R2 := ( { P, Z, R }, { PR → Z }).
Wtedy relacje E1 i E2 z tego przykładu są w 4PN.
Schemat relacyjnej bazy danych.
Definicja. Schematem relacyjnej bazy danych nazywamy zbiór wszystkich schematów relacyjnych występujących w danej bazie danych.
Algorytm tworzenia schematu relacyjnej bazy danych:
Określamy jeden schemat relacyjnej bazy danych { R := ( U, F ) }, gdzie U jest zbiorem wszystkich atrybutów występujących w bazie danych, przy czym zbiór U dobieramy w taki sposób aby można było na zbiorze U określić zależności funkcyjne.
Rozkładając schemat relacyjny R na schematy Ri := ( Ui , Fi ), i = 1,2,..,n otrzymamy schemat bazy danych ℜ := { Ri := ( Ui , Fi ) | i = 1,2,..,n }.
Projektowanie schematu bazy danych
Równoważność schematów.
Niech dane będą następujące schematy baz danych:
ℜ1 := { R := ( U, F ) },
ℜ2 := { Ri := ( Ui , Fi ) | i = 1,2,..,n }, U ![]()
(n ≥ 2).
Wprowadzimy definicje równoważności schematów ℜ1 i ℜ2.
Definicja. Mówimy, że schematy ℜ1 i ℜ2 są EQ1-równoważne, gdy dla każdej relacji R∈INST(ℜ1) ![]()
Definicja. Mówimy, że schematy ℜ1 i ℜ2 są EQ2-równoważne, gdy
.
Definicja. Mówimy, że schematy ℜ1 i ℜ2 są EQ3-równoważne, gdy są EQ1 i EQ2-równoważne.
Uwaga. Rozkład ℜ2 EQ1-równoważny rozkładowi ℜ1 jest rozkładem bez straty danych a EQ2-równoważny bez straty zależności.
Przy rozkładach schematów baz danych wymaga się zazwyczaj aby każdy z wynikowych schematów był w 3PN (4PN) i aby liczba ich była jak najmniejsza. Przedstawione zostaną następujące metody projektowania schematu baz danych:
algorytm dekompozycji,
algorytm Bernsteina,
algorytm Niekludowej - Calenki.
Algorytmy pomocnicze.
Sprowadzenie schematu relacyjnego do 2PN.
Sprowadzenie schematu relacyjnego do 3PN.
Rozstrzygnięcie, czy dla zadanych X,Y ⊂ U, zachodzi X →Y ∈ F +.
Usunięcie z lewej strony każdej zależności X →Y ∈ F + zbędnych atrybutów, tzn. takich atrybutów A ∈ X , dla których (X - A ) → Y ∈ F +.
Znalezienie minimalnego generatora zbioru F.
Sprawdzenie, czy dla zadanych dwóch zbiorów zależności F1 i F2 zachodzi równość .
Określenie wszystkich kluczy w schemacie R := ( U, F ) tzn. takich najmniejszych zbiorów atrybutów K ⊂ U , dla których K → U ∈ F +.
Algorytm dekompozycji.
Wyznaczyć wszystkie klucze w schemacie R.
Wykrywanie niepełnych zależności funkcyjnych i rozkład schematu relacyjnego ℜ na zbiór ℜ1 := {Ri := ( Ui , Fi ) | i = 1,2,..,m } schematów relacyjnych z których każdy jest w 2PN.
Wyznaczyć zbiory atrybutów kluczowych i niekluczowych w każdym schemacie relacyjnym Ri ∈ ℜ1.
Wykrywanie tranzytywnych zależności funkcyjnych w schematach relacyjnych Ri, i=1,2,..,m i sprowadzenie ich do 3PN.
Kluczami są zbiory: { P, I } i { I, G, S }.
Do dalszych rozważań weźmy klucz { P, I }. Niepełną zależnością funkcyjną w R jest np. zależność: PI→GSE, (bo P→GSE). Oznacza to, że schemat relacyjny R nie jest w 2PN. Przyjmując w algorytmie 1 K1:={ P } i X:={G, S, E } można R rozłożyć na dwa schematy
Wyznaczając atrybuty kluczowe otrzymamy dwa schematy relacyjne
Schematy te są już w 3PN i ℜ1 := {R1 , R2 } jest poszukiwanym rozkładem. Rozkład ten spowodował utratę zależności GI→P.
Algorytm Bernsteina.
Wyznaczyć zbiór F' składający się z wszystkich zależności funkcyjnych z F po wyeliminowaniu zbędnych atrybutów.
Wyznaczyć minimalny generator F0 zbioru F'.
Utworzyć zbiory Fi, i=1,2,...,m zaliczając do zbioru Fi te zależności z F', które posiadają identyczne lewe strony, które oznaczamy przez Xi. Zbiory te nazywamy grupami rozpiętymi nad F0.
Połączyć zbiory Fi i Fj gdy Xi →Xj∈F0+ i Xj →Xi∈F0+. Z tych zależności utworzyć zbiór J. Usunąć ze zbioru F0 wszystkie zależności postaci Xi →A i Xj →B gdzie A∈ Xj i B∈ Xi.
Usunąć ze zbioru F0 wszystkie zależności tranzytywne. W tym celu należy wyznaczyć taki najmniejszy zbiór F0', dla którego (F0'∪J)+ = (F0∪J)+. Każdą zależność funkcyjną z J należy dołączyć do odpowiadającej jej grupy w zbiorze grup rozpiętych nad F0'.
Dla każdej grupy utworzyć schemat relacyjny, którego atrybutami są wszystkie atrybuty występujące w tej grupie, a zbiór zależności funkcyjnych składa się ze wszystkich zależności z tej grupy. Każdy zbiór atrybutów występujących po lewej stronie dowolnej zależności funkcyjnej w grupie jest kluczem schematu.
F' = F = { XY→A, XY→D, CD→X, CD→Y, AX→B, BY→C, C→A }.
F0 = F'.
Tworzymy grupy rozpięte nad F0:
Korzystając z algorytmu 2 XY→CD∈F0+ , więc należy połączyć grupy F4 i F5. Ponadto
Ponieważ XY→CD∈F0+ więc XY→C∈F0+ i zależność XY→A jest zależnością tranzytywną, więc eliminując ją z F0 otrzymamy
Dla grup otrzymanych w punkcie 5 tworzymy zbiór schematów relacyjnych:
F' = F = { A→B, BC→D, D→BC }.
F0 = F'.
Tworzymy grupy rozpięte nad F0:
Ponieważ BC→D∈F0+ i D→BC∈F0+, więc należy połączyć grupy F2 i F3. Zatem
W F0 brak zależności tranzytywnych, więc
Dla grup otrzymanych w punkcie 5 tworzymy zbiór schematów relacyjnych:
Algorytm Niekludowej-Calenki.
Wyznaczyć wszystkie klucze w R i utworzyć zbiór atrybutów kluczowych UK.
Wyznaczyć najmniejszy podzbiór F' zbioru F, taki że { F'∪FD(UK) }+ = F+, gdzie FD(UK) oznacza projekcję zależności funkcyjnych ze zbioru F na zbiór UK.
Usunąć wszystkie zbędne atrybuty z zależności należących do F'.
Usunąć ze zbioru F' wszystkie zależności postaci K→A, gdzie K jest kluczem i utworzyć zbiór U1 z atrybutów A wchodzących w prawe strony wyrzuconych zależności i z atrybutów z UK.
Jeżeli U1 = U, to U jest w 3PN i zakończ działanie algorytmu.
Jeżeli U1 ≠ U, to przejdź do kroku 5.
Przez F'' oznaczyć zbiór zależności funkcyjnych pozostałych w F'. Przyjąć
Jeżeli U'≠ U, to wyznaczyć minimalny generator dla FD(U') i powtórzyć kroki 1-4 dla U'. Poszukiwany rozkład ℜ1 składa się z rozkładu U' i zbioru U1.
Jeżeli U = U' to należy zastosować algorytm Bernsteina.
Jeżeli w utworzonym rozkładzie chociażby jeden składnik zawiera klucz, to rozkład spełnia warunek EQ3-równoważności.
W przeciwnym wypadku poszukiwany rozkład składa się z utworzonego rozkładu i dowolnego klucza.
U = U1 ∪ U2∪ ... ∪ Un,
F+ = (F1 ∪ F2∪ ... ∪ Fn)+,
dla każdej relacji R ∈ INST(R) zachodzi
każdy schemat relacyjny Ri = ( Ui , Fi ) jest w 3PN,
liczba schematów w ℜ1 jest minimalna.
Kluczami w ℜ są { A,C }, { A,D }. Zatem UK = {A, C, D }.
FD(UK) = {D→C, C→D } i F'= { A→B, BC→D, D→B }.
F'= { A→B, BC→D, D→B }.
F'= { A→B, BC→D, D→B } i U1 = UK ≠ U.
F'' =F' i U'= { A, B, C, D }.
Ponieważ U'= U więc stosujemy algorytm Bernsteina, który daje U1 = { A, B } i U2= {B, C, D}. Ponieważ żaden z nich nie zawiera klucza więc rozszerzamy je o atrybuty należące do jednego z kluczy co spowoduje, że U2 = U. Zatem już schemat wyjściowy jest w 3PN i niepotrzebny jest rozkład.
Kluczami w ℜ są {X,Y}, {C,D} i {Y,B,D}. Zatem UK = {B, C, D, X, Y }.
FD(UK) = {XY→D, CD→X, CD→Y, BY→C } i F'= { AX→B, C→A }.
F'= { AX→B, C→A }.
F'= { AX→B, C→A } i U1 = UK ≠ U.
F'' =F' i U'= { A,B,C, X }≠U.
Kluczem w R' := ( U', F' ) jest {C,X}. Zatem U 'K= { C, X }.
FD(U 'K) = ∅ i (F')'= {AX→B, C→A }.
(F')'={AX→B, C→A }.
(F')'={AX→B, C→A }= F'.
(U')'=U.
Metody implementacji baz danych
Statyczny model pamiętania bazy danych
Dynamiczny model pamiętania bazy danych.
przekopiować wektory V1, MAP odpowiednio do V11, CMAP i podstawić STATUS(1) := 1;
np. modyfikowana jest strona 1 zapisana w bloku 2;
dla tej zmodyfikowanej strony szukamy w wektorze CMAP wolnego bloku do zapisania nowego stanu strony (może to być blok 3) i podstawiamy CMAP(3) := 1 oraz V1(1) := -3, (znak - oznacza stronę już zmienioną );
podobne kroki można przeprowadzić np. dla strony 2; po tych operacjach stan bazy danych można przedstawić przy pomocy następującego schematu:
możliwe są teraz dwa przypadki:
jeżeli zakończono tworzenie nowej wersji i nie stwierdzono błędu to
aktualne przyporządkowanie stron do bloków dane jest w wektorze V1;
gdy V1(i)<0 i V11(i) = j ≠ 0 to podstawiamy CMAP(j):= 0 i V1(i) := |V1(i)| dla i = 1, 2, ..., k;
aktualną mapę pamięci otrzymamy podstawiając MAP(i) := CMAP(i) dla i = 1, 2, ..., N;
zamykamy segment S1 podstawiając STATUS(1) := 0;
jeżeli w trakcie tworzenia nowej wersji stwierdzono błąd to
wracamy do pierwotnego wektora V1 podstawiając V1(i) := V11(i) dla i = 1, 2, ..., k;
aktualna mapa pamięci dana jest w wektorze MAP;
zamykamy segment S1 podstawiając STATUS(1) := 0;
Odwzorowanie rekordów na stronie.
każda wartość atrybutu zapisywana jest w polu o stałej długości (podanej w ilości znaków)
wartości wszystkich atrybutów zapisywane są w kolejnych polach o najmniejszym rozmiarze potrzebnym do ich zapamiętania i odseparowane wyróżnionym znakiem np. %
wartości wszystkich atrybutów zapisywane są w kolejnych polach o najmniejszym rozmiarze potrzebnym do ich zapamiętania i utworzenie dla każdego rekordu części przedrostkowej składającej się ze wskażników podających adresy końców poszczególnych pól
Adresowanie rekordów w bazie danych.
wprowadzanie rekordu,
usuwanie rekordu,
modyfikacja rekordu,
poszukiwanie rekordu o określonej wartości atrybutu.
adres pośredni złożony z numeru strony i przesunięcia na stronie,
adres bezpośredni w segmencie,
identyfikator wewnętrzny rekordu ( KBD ) składający się z dwóch części:
identyfikatora typu rekordu, którego wystąpieniem jest rozważany rekord,
kolejnego numeru przypisanemu rozważanemu rekordowi przez SZBD w obrębie zbioru wszystkich rekordów tego samego typu.
adres bezpośredni,
adres pośredni,
numer strony segmentu,
identyfikator względny złożony z dwóch pozycji: numeru strony i adresu wskaźnika na stronie, którego aktualna wartość jest adresem rekordu na stronie.
Wyszukiwanie rekordów w pliku
j:=0,
przyjmujemy k>0 takie, że j+k≤m,
przyjmujemy i:=j+k , sprowadzamy stronę si i jeżeli wartość klucza głównego ostatniego rekordu na tej stronie jest:
mniejsza od x - przechodzimy do punktu 4),
równa x - znaleziono szukany rekord - koniec algorytmu,
większa od x - przechodzimy do punktu 5),
przyjmujemy j:=i i przechodzimy do punktu 3),
szukany rekord znajduje się na jednej ze stron si-k+1, ... , si ,
jeżeli
k=1 to przeglądamy sekwencyjnie stronę si - kończymy algorytm,
k>1 to przyjmujemy j:=i-k+1 i m:=i - przechodzimy do punktu 2),
Organizacja dostępu do pliku rekordów za pomocą B-drzewa.
Pojęcie B-drzewa.
wszystkie drogi prowadzące z korzenia do liści są jednakowej długości równej h;
każdy wierzchołek, z wyjątkiem korzenia i liści, jest początkiem co najmniej m+1 krawędzi;
korzeń jest liściem lub jest początkiem co najmniej dwóch krawędzi;
każdy wierzchołek jest początkiem co najwyżej 2m+1 krawędzi.
1 ≤ l ≤ 2m w przypadku korzenia i m ≤ l ≤ 2m dla wierzchołków pośrednich i liści; wartość l jest liczbą elementów indeksu na stronie,
xi wartością klucza głównego wystąpienia rekordu, ai kluczem bazy danych odpowiadającym wystąpieniu rekordu o wartości klucza głównego xi, 1 ≤ i ≤ l,
pi wskażnikiem na wierzchołek będącym końcem krawędzi wychodzącej z tego wierzchołka, 0 ≤ i ≤ l,
x1 < x2 < ... < xl,
Niech P(pi) oznacza wierzchołek wskazywany przez wskaźnik pi, 0 ≤ i ≤ l, a X(pi) niech będzie zbiorem wartości klucza głównego zawartym w poddrzewie, którego korzeniem jest P(pi).
( ∀ x ∈ X(p0) ) (x < x1 ),
( ∀ x ∈ X(pi) ) (xi < x < xi+1 ), dla 1 ≤ i < l,
( ∀ x ∈ X(pl) ) (xl < x ).
Algorytm wyszukiwania w pliku indeksowym zorganizowanym w postaci B-drzewa.
Pod p podstawiamy identyfikator strony korzenia i przyjmujemy s := null.
Czy p ≠ null ?
Jeżeli tak, to s := p i przechodzimy do punktu 3.
Jeżeli nie to kończymy algorytm (oznacza to, że w indeksie I brak poszukiwanego elementu).
Sprowadzamy do pamięci stronę wskazywaną przez p.
Czy x < x1 ?
Jeżeli tak, to p = p0 i przechodzimy do punktu 2.
Jeżeli nie, to przechodzimy do punktu 5.
Czy istnieje takie i, że x = xi ?
Jeżeli tak, to a := ai i jest to koniec algorytmu; a jest poszukiwanym elementem tzn. (x,a)∈I.
Jeżeli nie, to przechodzimy do punktu 6.
Czy istnieje takie i, że xi < x < xi+1 ?
Jeżeli tak, to p = pi i przechodzimy do punktu 2.
Jeżeli nie, to p = pl i przechodzimy do punktu 2.
Jeżeli s1 leży na lewo od strony s, to elementy (xk,ak), k = 1,2,...,i-1 wstawiamy na stronę s1, a elementy (xk,ak), k = i+1,i+2,...,2m+j+2 na stronę s.
Algorytm dołączania do B-drzewa.
Stosujemy algorytm wyszukiwania dla klucza głównego x.
Czy znaleziono x ?
Jeżeli nie, to przechodzimy do punktu 3.
Jeżeli tak, to koniec algorytmu (oznacza to, że w indeksie I już występuje element (x,a)).
Czy wartość s jest niezerowa (s z algorytmu wyszukiwania)?
Jeżeli tak, to przechodzimy do punktu 4.
Jeżeli nie, to drzewo jest puste, utwórz stronę korzenia i dołącz do niej element (x,a), koniec algorytmu.
Czy strona s zawiera mniej niż 2m elementów?
Jeżeli tak, to dołącz element (x,a) do strony s i jest to koniec algorytmu.
Jeżeli nie, to przechodzimy do punktu 5.
Czy s jest liściem ?
Jeżeli tak, to przechodzimy do punktu 6.
Jeżeli nie, to przechodzimy do punktu 7.
Czy można dokonać kompensacji?
Jeżeli tak, dokonujemy kompensacji dołączając element (x,a) i kończymy algorytm.
Jeżeli nie, to przechodzimy do punktu 7.
Dokonujemy podziału strony s dołączając parę (x,a).
Czy umieszczenie elementu (xm+1,am+1) w wierzchołku krawędzi, której końcem jest strona s jest możliwe?
Jeżeli nie, to pod (x,a) podstawiamy (xm+1,am+1) a symbolem s oznaczamy stronę będącą do tej pory początkiem krawędzi kończącej się na stronie s i przechodzimy do punktu 6.
Jeżeli tak, to dołączmy element (xm+1,am+1) do stronę będącej początkiem krawędzi kończącej się na stronie s i kończymy algorytm.
Algorytm usuwania z B-drzewa.
zawarte w niej j elementów pozostawiamy bez zmian,
na miejsce j+1 na wstawiamy element (xi,ai) ze strony s2,
następnie wstawiamy wszystkie elementy ze strony s1,
stronę s1 przekazujemy do puli stron wolnych,
ze strony s2 usuwamy element (xi,ai) wraz ze wskaźnikiem p' leżącym po prawej stronie elementu (xi,ai) i jeżeli strona ta stanie się stroną pustą, (jest to w przypadku, gdy s2 jest korzeniem zawierającym tylko jeden element ), to również przekazujemy ją do puli stron wolnych.
Stosujemy algorytm wyszukiwania dla klucza głównego x.
Czy znaleziono x ?
Jeżeli tak, to przechodzimy do punktu 3.
Jeżeli nie, to koniec algorytmu (oznacza to, że w indeksie I już nie występuje element (x,a)).
Czy wartość s wskazuje stronę liścia (s z algorytmu wyszukiwania)?
Jeżeli nie, to przechodzimy do punktu 4.
Jeżeli tak, to usuwamy element (x,a) i przechodzimy do punktu 6.
Wyszukujemy stronę liścia przechodząc po wskaźnikach p0 w poddrzewie, którego korzeń wskazywany jest przez wskaźnik p znajdujący się z prawej strony elementu (x,a).
Element (x,a) zastępujemy pierwszym elementem z wyszukanej strony liścia i usuwamy ten element ze strony liścia.
Czy wystąpił niedomiar?
Jeżeli nie, to koniec algorytmu, (usuwanie zakończone powodzeniem).
Jeżeli tak, to przechodzimy do punktu 7.
Czy możliwa jest likwidacja niedomiaru metodą łączenia?
Jeżeli nie, to przeprowadzamy kompensację i koniec algorytmu, (usuwanie zakończone powodzeniem).
Jeżeli tak, to przeprowadzamy łączenie i przechodzimy do punktu 6.
Organizacja dostępu do pliku rekordów za pomocą B*-drzewa.
Pojęcie B*-drzewa i organizacja indeksu pliku według B*-drzewa.
dla wierzchołka będącego korzeniem lub wierzchołkiem pośrednim
1 ≤ l ≤ 2m* w przypadku korzenia i m* ≤ l ≤ 2m* dla wierzchołków pośrednich; wartość l jest liczbą kluczy głównych na stronie;
xi wartością klucza głównego wystąpienia rekordu, 1 ≤ i ≤ l;
pi wskażnikiem na wierzchołek będącym końcem krawędzi wychodzącej z tego wierzchołka, 0 ≤ i ≤ l;
dla wierzchołka będącego liściem
j oznacza liczbę elementów indeksu na strone, m ≤ j ≤ 2m;
( xi , ai ) elementy indeksu, 1 ≤ i ≤ j,
x1 < x2 < ... < xl, dla wierzchołków nie będących liśćmi i x1 < x2 < ... < xj, dla wierzchołków będących liśćmi;
Niech P(pi) oznacza wierzchołek wskazywany przez wskaźnik pi, 0 ≤ i ≤ l, a X(pi) niech będzie zbiorem wartości klucza głównego zawartym w poddrzewie, którego korzeniem jest P(pi).
( ∀ x ∈ X(p0) ) ( (x ≤ x1 ) ∧ ( max{x | x∈ X(p0) }= x1 ) ) ),
( ∀ x ∈ X(pi) ) ( (xi < x ≤ xi+1 ) ∧ ( max{x | x∈ X(p0) }= xi+1 ) ) ), dla 1 ≤ i < l,
( ∀ x ∈ X(pl) ) (xl < x ).
Organizacja pliku rekordów przy pomocy B*-drzewa
w liściach rekordy są uporządkowane według klucza głównego,
w liściach mogą być umieszczane dodatkowe informacje lokalizujące sąsiednie liście, co umożliwia dostęp do całego pliku rekordów w kolejności rosnącej (malejącej) wartości klucza głównego.
Organizacja dostępu do pliku rekordów według argumentów wyszukiwania nie będących kluczami głównymi.
Sformułowanie zadania.
łączenie w łańcuch (dane pomocnicze pamiętane są łącznie z rekordami);
struktury odwrócone (dane pomocnicze pamiętane są oddzielnie):
z tablicami adresowymi;
z tablicami binarnymi.
Struktury łańcuchowe.
skorowidz atrybutów, (SA);
skorowidz wartości atrybutów, (SWA);
skorowidz początków łańcuchów, (SPŁ).
określenie informacji o początku i długości łańcucha odpowiadającego wartości atrybutów "czerwony" i "Fiat".
wczytywanie rekordów należących do łańcucha o najmniejszej długości ("czerwony") i sprawdzanie, czy rekordy te (703,812,903) spełniają kryterium wyszukiwania.
Struktury odwrócone z tablicami adresowymi.
skorowidz atrybutów, (SA);
skorowidz wartości atrybutów, (SWA);
skorowidz tablic adresowych, (STA).
Struktury odwrócone z tablicami binarnymi.
Podstawy strukturalnego języka zapytań SQL
Typy danych
Spis typów danych
Typ numeryczny
Konwersje typów
Wartości puste
Rozkazy języka SQL
Spis rozkazów języka SQL
rozkazy definicji danych - (Date Definition Language - DDL),
rozkazy manipulowania danymi - (Data Manipulation Language - DML),
rozkazy sterowania transakcjami - (Data Control Language - DCL).
Definicje podstawowe
7E2 = 7 * 102
25e-03 = 25 * 10-3
256K = 256 * 1024
1M = 1 * 1048576
Rozkaz CREATE TABLE
określenie sposobu alokacji przestrzeni do przechowywania danych
określenie rozmiaru tabeli
przydzielenie tabeli do określonego klastra
załadowanie danych będących wynikiem podanego zapytania, do tabeli
user - właściciel tabeli, jeśli nie zostanie podany, to właścicielem staje się osoba tworząca tabelę. Tabele dla innych użytkowników może tworzyć tylko administrator systemu zarządzania bazą danych (DBA)
table - nazwa tabeli, powinna być prawidłowym identyfikatorem. Wszystkie obiekty danego użytkownika powinny mieć unikalne nazwy
column_element - definiuje kolumnę i opcjonalne ograniczenia na wartości w tej kolumnie. Tabela musi zawierać co najmniej jedną kolumnę (jak to wynika ze składni)
table_constraints - określa ograniczenia jakie musi spełniać cała tabela
tablespace - określa obszar, w którym należy umieścić tabelę
storage - określa przyszły sposób alokacji pamięci
cluster - określa klaster (którego właścicielem musi być właściciel tabeli), do którego należy przydzielić tabelę
query - jest poprawnym zapytaniem takim samym jak zdefiniowane w rozkazie SELECT. Jeśli podane jest zapytanie, to można podać tylko nazwy kolumn - typy i rozmiary są kopiowane z odpowiednich kolumn określonych w zapytaniu. Możliwe jest również pominięcie nazw kolumn, ale tylko wtedy, gdy nazwy te są unikalne i dobrze zdefiniowane w zapytaniu. Liczba wyspecyfikowanych kolumn musi być taka sama jak liczba kolumn w zapytaniu.
Rozkaz DROP
DROP CLUSTER [user.]cluster [INCLUDING TABLES] - kasowanie klastra. W przypadku podania klauzuli INCLUDING TABLES zostaną skasowane wszystkie tabele przydzielone uprzednio do kasowanego klastra. Jeśli klauzula INCLUDING TABLES nie zostanie podana, to przed skasowaniem klastra muszą być skasowane wszystkie należące do niego tabele. Jest to zabezpieczenie przed omyłkowym skasowaniem klastra zawierającego tabele, które są potrzebne.
DROP [PUBLIC] DATABASE LINK link - usuwanie połączenia. Jeśli połączenie jest publiczne to skasować je może tylko administrator (DBA).
DROP INDEX [user.]index - kasowanie indeksu.
DROP [PUBLIC] ROLLBACK SEGMENT segment - kasowanie segmentu wycofywania (rollback). Można usunąć tylko te segmenty wycofywania, które nie są używane w danym momencie. Kasowanie segmentów wycofywania może wykonywać tylko administrator bazy danych.
DROP SEQUENCE [user.]sequence - kasowanie sekwencji.
DROP [PUBLIC] SYNONYM [user.]synonym - usuwanie synonimu. Synonim publiczny może zostać usunięty tylko przez administratora (DBA). Poszczególni użytkownicy mogą usuwać tylko te segmenty, których są właścicielami.
DROP TABLE [user.]table - usuwanie tabeli. W momencie usunięcia tabeli automatycznie kasowane są skojarzone z nią indeksy zarówno utworzone przez właściciela tabeli jak i przez innych użytkowników. Widoki i synonimy wskazujące na tabelę nie są kasowane automatycznie, ale stają się nieprawidłowe.
DROP TABLESPACE tablespace [INCLUDING CONTENTS] - usuwanie obszaru danych. Rozkaz ten może być wykonany tylko przez administratora (DBA). W przypadku podania klauzuli INCLUDING CONTENTS obszar danych zostanie skasowany nawet wtedy, gdy zawiera dane. Jeśli klauzula INCLUDING CONTENTS nie została podana, a obszar zawiera dane, to nie zostanie skasowany.
DROP VIEW [user.]view - usuwanie widoku. Po usunięciu widoku, inne widoki lub synonimy, które odwoływały się do widoku skasowanego, nie zostaną skasowane, ale stają się nieprawidłowe.
Rozkaz INSERT
user - nazwa właściciela tabeli
table - nazwa tabeli, do której dopisywane są wiersze
column - nazwa kolumny wewnątrz tabeli lub widoku
value - pojedyncza wartość odpowiadająca odpowiedniej pozycji na liście
kolumn. Wartość może być dowolnym wyrażeniem. Jeśli wprowadzana wartość nie jest równa NULL to musi być zgodna z typem wartości kolumny, do której zostanie dopisana.
query - prawidłowy rozkaz SELECT, który zwraca taką ilość wartości jak podana w liście określającej kolumny. Zapytanie nie może mieć klauzuli ORDER FOR ani FOR UPDATE.
INSERT INTO pracownicy
INSERT INTO ksiazki (tytul, autor, miejsce)
Rozkaz DELETE
user - nazwa użytkownika
table - nazwa tabeli lub widoku, z którego należy usunąć wiersze
alias - nazwa aliasu odnoszącego się do tabeli, który jest używany w rozkazie DELETE z powiązanymi zapytaniami
condition - warunek jaki muszą spełniać wiersze, które należy usunąć. Warunek ten może odwoływać się do tabeli, na której przeprowadza się operację i zawierać powiązane z nim zapytania. Konieczne jest jednak, by warunek, dla każdego z wiersza podanej tabeli, był obliczany do wartości TRUE lub FALSE.
Skasowanie wszystkich wierszy w tabeli pracownicy:
Skasowanie wszystkich wierszy zawierających książki, których autor oznaczony jest numerem 2:
Rozkaz CREATE SEQUENCE
user - nazwa użytkownika
sequence - nazwa tworzonej sekwencji, musi być poprawnym identyfikatorem i być unikalna w obrębie danego użytkownika.
INCREMENT BY - określa różnicę między kolejno generowanymi liczbami. Jeśli liczba ta jest ujemna, to będą generowane liczby w porządku malejącym, w przeciwnym wypadku - w porządku rosnącym. Domyślnie przyjmowana jest wartość 1. Dozwolona jest każda liczba różna od 0.
START WITH - pierwsza liczba, która powinna być wygenerowana przez sekwencję. Domyślną wartością jest MINVALUE dla sekwencji rosnących i MAXVALUE dla sekwencji malejących. Utworzona sekwencja nie jest zainicjalizowana i pierwszą wartość otrzymuje się po jednokrotnym odczytaniu pseudokolumny NEXTVAL.
MINVALUE - określa minimalną wartość jaką może wygenerować sekwencja. Domyślnie dla sekwencji rosnących jest to 1, natomiast dla malejących wartość ta wynosi -10e27 + 1. Podanie NOMINVALUE powoduje, że sekwencja nie będzie sprawdzać wartości minimalnej.
MAXVALUE - określenie maksymalne wartości, jaką może wygenerować sekwencja. Wartościami domyślnymi są -1 i 10e27 - 1 odpowiednio dla sekwencji malejącej i rosnącej. Wyspecyfikowanie NOMAXVALUE powoduje, że sekwencja nie będzie sprawdzać wartości maksymalnej.
CYCLE, NOCYCLE - domyślną wartością jest NOCYCLE, które powoduje, że żadne dodatkowe numery nie zostaną wygenerowane po osiągnięciu końca sekwencji. W tym wypadku każda próba generacji kolejnego numeru spowoduje zgłoszenie błędu. W przypadku podania klauzuli CYCLE po osiągnięciu wartości maksymalnej sekwencja powróci do wartości minimalnej (dla sekwencji rosnących) lub po osiągnięciu wartości minimalnej powróci do maksymalnej (dla sekwencji malejących) rozpoczynając kolejny cykl generacji numerów.
CACHE, NOCACHE - klauzula CACHE włącza wykonywanie pre-alokacji numerów sekwencji i przechowywanie ich w pamięci, co skutkuje zwiększeniem szybkości generacji kolejnych liczb. Klauzula NOCACHE wyłącza tę możliwość. Domyślnie przyjmowane jest CACHE 20. Wartość podana w CACHE musi być mniejsza niż MAXVALUE - MINVALUE.
ORDER, NOORDER - klauzula ORDER gwarantuje, że kolejne liczby będą generowane w porządku jakim otrzymane zostały przez system polecenia ich generacji. Klauzula NOORDER wyłączą tę własność. Kolejność generacji numerów w sekwencji jest ważna w aplikacjach, w których ważna jest kolejność (czasowa) wykonywanych operacji. Zwykle nie jest ona ważna w aplikacjach, które wykorzystują sekwencje tylko do generacji kluczy pierwotnych.
w klauzuli SELECT i rozkazie SELECT (z wyjątkiem widoków),
liście wartości rozkazu INSERT,
wyrażeniu SET w rozkazie UPDATE.
Rozkaz SELECT
ALL - ustawiane domyślnie, oznacza, że wszystkie wiersze, które spełniają warunki rozkazu SELECT powinny zostać pokazane.
DISTINCT - określa, że wiersze powtarzające się powinny zostać usunięte przed zwróceniem ich na zewnątrz. Dwa wiersze traktuje się jako równe jeśli wszystkie wartości dla każdej z kolumn zwracanych rozkazem SELECT są sobie równe.
* - oznacza, że wszystkie kolumny ze wszystkich wymienionych tabel powinny zostać pokazane.
table.* - oznacza, że wszystkie kolumny z podanej tabeli powinny zostać pokazane
expr - wyrażenie, zostanie opisane w dalszej części wykładu
c_alias - jest inną nazwą dla kolumny (aliasem) i powoduje, że nazwa ta zostanie użyta jako nagłówek kolumny podczas wyświetlania. W żaden sposób nie jest zmieniana rzeczywista nazwa kolumny. Aliasy kolumn nie mogą być używane w dowolnym miejscu zapytania.
[user.]table - określa które tabele i widoki należy pokazać. Jeśli użytkownik nie jest podany to domyślnie przyjmowany jest użytkownik aktualny (wykonujący rozkaz SELECT).
t_alias - pozwala określić inną nazwę dla tabeli w celu obliczenia zapytania. Najczęściej jest używane w zapytaniach powiązanych. W tym wypadku inne odwołania do tabeli wewnątrz zapytania muszą posługiwać się wyspecyfikowanym aliasem.
condition - warunek, jaki muszą spełniać wiersze, aby zostały zwrócone przez zapytanie. Warunki zostaną opisane dokładniej w dalszej części wykładu.
position - identyfikuje kolumnę bazując na jej tymczasowym położeniu w rozkazie SELECT, a nie na nazwie.
ASC, DESC - określa, że zwracane wiersze powinny być posortowane w kolejności rosnącej lub malejącej (odpowiednio).
column - nazwa kolumny należąca do jednej z tabel podanych w klauzuli FROM.
NOWAIT - określa, że ORACLE powinien zwrócić sterowanie do użytkownika, zamiast czekać na możliwość zablokowania wiersza, który został uprzednio zablokowany przez innego użytkownika.
jeśli dwie tabele mają kolumny o tej samej nazwie, to nie wiadomo, która powinna być użyta w rozkazie SELECT
ORACLE wykonuje znacznie mniej obliczeń, jeśli nazwy te są podane i nie trzeba ich szukać.
SELECT imie, nazwisko FROM pracownicy ;
SELECT tytul, autorzy.imie, autorzy.nazwisko, miejsca.miejsce
Rozkaz UPDATE
user - nazwa właściciela tabeli.
table - nazwa istniejącej tabeli.
alias - dodatkowa nazwa używana do dostępu do tabeli w pozostałych klauzulach rozkazu.
column - kolumna wewnątrz tabeli. Nawiasy nie są potrzebne jeśli lista kolumn zawiera tylko jedną kolumnę.
expr - wyrażenie - zostanie opisane w dalszej części wykładu
query - rozkaz SELECT bez klauzul ORDER BY i FOR UPDATE, często skorelowany ze zmienianą tabelą.
condition - poprawny warunek. Warunek musi zwracać wartość TRUE lub FALSE.
Rozkaz RENAME
old - aktualna nazwa tabeli, widoku lub synonimu
new - żądana nazwa tabeli, widoku lub synonimu
Rozkaz CREATE INDEX
UNIQUE - zakłada, że tabela nie ma nigdzie dwóch wierszy zawierających te same wartości we wszystkich indeksowanych kolumnach. W aktualnej wersji ORACLE'a jeśli indeks typu UNIQUE nie zostanie utworzony dla tabeli, to tabela może zawierać powtarzające się wiersze.
indeks - nazwa tworzonego indeksu. Nazwa ta musi być inna od każdego innego obiektu bazy danych danego użytkownika.
table - nazwa istniejącej tabeli, dla której tworzy się indeks.
column - nazwa kolumny w tabeli.
ASC, DESC - zostały dodane w systemie ORACLE w celu zapewnienia kompatybilności z systemem DB2, ale zawsze są tworzone w porządku rosnącym.
CLUSTER cluster - określa klaster, dla którego tworzony jest indeks.
NOSORT - wskazuje ORACLE'owi, że wiersze przechowywane w bazie są już posortowane, w związku z czym nie jest konieczne sortowanie podczas tworzenia indeksu.
Rozkaz CREATE VIEW
user - właściciel tworzonego widoku.
view - nazwa tworzonego widoku.
query - identyfikuje kolumny i wiersze tabel, na których bazuje widok. Zapytanie może być dowolnym poprawnym rozkazem SELECT nie zawierającym klauzul ORDER BY ani FOR UPDATE.
WITH CHECK OPTION - informuje, że wstawienia i zmiany wykonywane poprzez widok, są niedozwolone jeśli spowodują wygenerowanie wierszy, które będą niedostępne dla widoku. Klauzula WITH CHECK OPTION może być użyta w widoku bazującym na innym widoku.
CONSTRAINT - nazwa dołączona do warunku WITH CHECK OPTION.
widok nie przechowuje danych - jest on przeznaczony do pokazywania danych zawartych w innych tabelach.
widok może być użyty w rozkazie SQL w dowolnym miejscu, w którym możliwe jest użycie tabeli z zastrzeżeniem, że można wykonywać selekcję z widoku tylko wtedy, gdy zapytanie na którym bazuje widok zawiera:
połączenie ,
klauzule GROUP BY, CONNECT BY lub START WITH ,
klauzulę DISTINCT, pseudokolumny lub wyrażenia na liście kolumn.
utworzenia dodatkowego poziomu zabezpieczenia tabeli poprzez ograniczenie dostępu do określonych kolumn lub wierszy tabeli bazowej
ukrycia złożoności danych - na przykład widok może być użyty do operacji na wielu tabelach tak, by wydawało się, że operacje wykonywane są na jednej tabeli.
pokazywania danych z innej perspektywy - dla przykładu widok może zostać użyty do zmiany nazwy kolumny bez zmiany rzeczywistych danych zapisanych w tabeli.
zapewnienia poziomu integralności.
Rozkaz COMMIT
Rozkaz ROLLBACK
WORK - opcjonalne, wprowadzone tylko dla kompatybilności ze standardem ANSI
SAVEPOINT - opcjonalne, nie zmienia działania rozkazu ROLLBACK
savepoint - nazwa punktu zaznaczonego podczas wykonywania aktualnej transakcji.
ROLLBACK ;
ROLLBACK TO SAVEPOINT SP5 ;
Rozkaz SAVEPOINT
savepoint - nazwa punktu w aktualnej transakcji zaznaczanego przez wykonywany rozkaz
UPDATE pracownicy
UPDATE pracownicy
SELECT SUM(placa_podstawowa) FROM pracownicy;
UPDATE pracownicy
Rozkaz SET TRANSACTION
READ ONLY - klauzula, która musi wystąpić
Operacje na relacjach
Selekcja
Projekcja
Produkt
Połączenie
Wyrażenia
kolumna, stała lub wartość specjalna
[table.] { column | ROWID }
text
number
sequence.CURRVAL
sequence.NEXTVAL
NULL
ROWNUM
LEVEL
SYSDATE
UID
USER
pracownicy.nazwisko
'to jest ciąg znaków'
10
SYSDATE
zmienna łączona z opcjonalną zmienną indykatorową
:nazwisko_pracownika:nazwisko_pracownika_indykator
:położenie_wydziału
wywołanie funkcji
LENGTH('Kowalski')
ROUND(1234.567*82)
kombinacja wyrażeń wymienionych w poprzednich punktach
(expr)
+expr, -expr, PRIOR expr
expr * expr, expr / expr
expr + expr, expr - expr, expr || expr
('Kowalski: ' || 'Nauczyciel')
LENGTH('Nowak') * 57
SQRT(144) + 72
lista wyrażeń w nawiasach
('Kowalski', 'Nowak', 'Burzynski')
(10, 20, 40)
(LENGTH('Kowalski') * 5, -SQRT(144) + 77, 59)
liście kolumn w rozkazie SELECT
jako warunek w klauzulach WHERE i HAVING
w klauzulach CONNECT BY, START WITH, ORDER BY
klauzuli VALUE w rozkazie INSERT
w klauzuli SET rozkazu UPDATE
Warunki
porównanie z wyrażeniem lub wynikiem zapytania
<expr> <comparison operator> <expr>
<expr> <comparison operator> <query>
<expr-list> <equal-or-not> <expr-list>
<expr-list> <equal-or-not> <query>
porównanie z dowolnym lub ze wszystkimi elementami listy lub zapytania
<expr> <comparison> { ANY | ALL }
( <expr> [, <expr] ...)
<expr> <comparison> { ANY | ALL } <query>
<expr-list> <equal-or-not> { ANY | ALL }
( <expr-list> [, <expr_list>] ...)
<expr-list> <equal-or-not> { ANY | ALL } <query>
sprawdzenie przynależności do listy lub zapytania
<expr> [NOT] IN ( <expr> [, <expr>] ... )
<expr> [NOT] IN <query>
<expr-list> [NOT] IN
( <expr-list> [, <expr-list>] ... )
<expr-list> [NOT] IN <query>
sprawdzenie przynależności do zakresu wartości
sprawdzenie czy wartość jest równa NULL
sprawdzenie czy zapytanie zwróciło jakiekolwiek wiersze
kombinacja innych warunków (podana zgodnie z priorytetami)
( <condition> )
NOT <condition>
<condition> AND <conditin>
<condition> OR <condition>
Nazwisko = 'Kowalski'
pracownicy.Wydzial = Wydzialy.Wydzial
Data_urodzenia > '01-JAN-67'
Zawod IN ('Dyrektor', 'Urzednik', 'Informatyk')
Placa BETWEEN 500 AND 1500 ;
Funkcje
Funkcje numeryczne
ROUND(16.167, 1).
ROUND(16, 167, -1).
TRUNC(15.79,1) Wynik: 15.7,
TRUNC(15.79, -1). Wynik: 10
Funkcje znakowe
Funkcje grupowe
Funkcje konwersji
Funkcje operacji na datach
Inne funkcje
Formaty danych
Formaty zapisu danych
zmiany sposobu wyświetlania informacji w kolumnie;
wprowadzanie danej zapisanej inaczej niż domyślnie
Formaty numeryczne
Formaty dat
FM - "Fill Mode" przełącznik włączający/wyłączający wypełnianie tekstów spacjami i liczb zerami;
TH - dodany po kodzie pola powoduje wyświetlanie liczby porządkowej np. 4TH dla liczby 4;
SP - dodany po kodzie pola powoduje, że jest ono literowane ;
SPTH lub THSP - połączenie SP i TH.
Warunki i wyrażenia
Operatory arytmetyczne
... WHERE NR = -1
... WHERE -PLACA < 0
Operatory znakowe
Operatory porównania
... WHERE ZAWOD IN ('URZEDNIK', 'INFORMATYK')
... WHERE PLACA IN (SELECT PLACA FROM PRAC WHERE WYDZIAL=30)
... WHERE PLACA = ANY
(SELECT PLACA FROM PRAC
Operatory logiczne
...WHERE NOT (zawod IS NULL)
...WHERE NOT (A=1)
Operatory mnogościowe
Optymalizacja zapytań.
plik FR zawiera r rekordów, a FS s rekordów;
blok zawiera br rekordów z FR i bs rekordów z FS;
w RAM jest miejsce na m rekordów.
liczba dostępów do bloków niezbędnych do odczytania
pliku FR wynosi
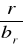
,pliku FS wynosi
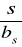
plik FR trzeba odczytać
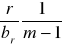
razy, przy czym za każdym razem potrzeba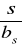
dostępów do bloków pliku FS.dla obu plików można stworzyć indeksy względem B i względem C,
można stworzyć indeks względem B lub względem C. Niech np. istnieje indeks względem B. Wtedy wystarczy raz przebiec plik FS i dla każdej wartości atrybutu C poszukać w pliku FR rekordów o wartości atrybutu B równej atrybutowi C.
Podstawy programowania w strukturalnym języku zapytań PL/SQL.
Wprowadzenie.
Struktura bloku
Procedury i funkcje
Kursory
jawnych - użytkownik może w sposób jawny utworzyć kursor dla zapytań, których wynikiem jest wiele wierszy i wykonywać operacje na tych wierszach (najczęściej za pomocą rozkazu FOR);
niejawnych - PL/SQL automatycznie tworzy kursor dla wszystkich pozostałych operacji.
%NOTFOUND - TRUE, jeśli ostatni rozkaz FETCH zakończył się niepowodzeniem z powodu braku wierszy
%FOUND - TRUE, jeśli ostatni rozkaz FETCH zakończył się sukcesem
%ROWCOUNT - liczba wierszy w kursorze (po otwarciu kursora)
%ISOPEN - TRUE, jeśli kursor jest otwarty
Rekordy
przypisanie zawartości jednego rekordu do drugiego (deklaracje obu rekordów muszą odwoływać się do tego samego kursora lub tabeli;
wstawienie wartości do rekordu rozkazem SELECT ... INTO lub FETCH ... INTO
Obsługa błędów
Informacje podstawowe
Wyjątki predefiniowane
CURSOR_ALREADY_OPEN - wywoływany w przypadku próby otwarcia kursora już otwartego;
DUP_VAL_ON_INDEX - wywoływany w przypadku próby wykonania rozkazu INSERT lub UPDATE, który spowodowałby utworzenie dwóch takich samych wierszy w indeksie zadeklarowanym jako UNIQUE;
INVALID_CURSOR - wywoływany w przypadku próby dostępu do nieprawidłowego kursora (np. nie otwartego);
INVALID_NUMBER - wywoływany w przypadku próby wykonania konwersji do typu numerycznego z tekstu, który nie reprezentuje liczby;
NO_DATA_FOUND - wywoływany wtedy, gdy rozkaz SELECT powinien zwrócić jeden wiersz a nie zwraca żadnego (np. SELECT ... INTO);
STORAGE_ERROR - wywoływany w przypadku braku wolnej pamięci lub uszkodzenia zawartości pamięci;
TOO_MANY_ROWS - wywoływany w przypadku, gdy rozkaz SELECT zwraca więcej niż jeden wiersz, a oczekiwany jest tylko jeden (np. SELECT ... INTO);
VALUE_ERROR - wywoływany w przypadku przypisania złej wartości do zmiennej lub pola;
ZERO_DIVIDE - próba dzielenia przez zero;
Obsługa wyjątków
Wyjątki zdefiniowane przez użytkownika
Rozkazy
Rozkaz OPEN
cursor_name - nazwa kursora uprzednio zadeklarowanego, który nie jest aktualnie otwarty.
input_parameter - wyrażenie języka PL/SQL, które przekazywane jest do kursora. Jest ono najczęściej używane do wykonania zapytania (najczęściej stosowane jest w klauzuli WHERE).
Rozkaz CLOSE
Rozkaz FETCH
cursor_name - nazwa aktualnie otwartego kursora.
variable_name - prosta zmienna, do której zostaną zapisane dane. Wszystkie zmienne na liście muszą być uprzednio zadeklarowane. Dla każdej kolumny w kursorze, musi wystąpić odpowiadająca jej zmienna. W dodatku typy kolumn muszą być takie same jak odpowiadające im typy zmiennych lub konwertowalne do nich.
record_name - nazwa zmiennej będącej rekordem (deklarowanej z użyciem atrybutu %ROWTYPE).
Rozkaz SELECT ... INTO
Rozkaz IF
plsql_condition - warunek (wyrażenie obliczane do wartości logicznej)
seq_of_statements - ciąg instrukcji, które mają być wykonane w razie spełnienia (bądźĽ nie spełnienia) podanego warunku
Rozkaz LOOP
label_name - ten parametr pozwala na opcjonalne nazwanie pętli. Możliwe jest wtedy użycie nazwy pętli w rozkazie EXIT w celu określenie, z której pętli powinno nastąpić wyjście. Ponadto możliwy jest dostęp do indeksu pętli zewnętrznej w pętli wewnętrznej, jeśli indeksy te mają tę samą nazwę za pomocą konstrukcji:
label_name.index
seq_of_statements - ciąg rozkazów, które będą powtarzane w pętli
plsql_condition - warunek języka PL./SQL. W pętli WHILE warunek ten jest obliczany przed każdą iteracją. Odpowiedni ciąg instrukcji wykonuje się tylko wtedy, gdy warunek ten ma wartość TRUE. W przeciwnym wypadku sterowanie przechodzi do pierwszej instrukcji za pętlą.
index - zmienna sterująca pętli FOR. Nie jest konieczna wcześniejsza jej deklaracja.
integer_expr - wyrażenie, którego wynikiem jest liczba całkowita. Wyrażenie to jest obliczane tylko przy pierwszym wejściu do pętli FOR.
REVERSE - klauzula, nakazująca zmniejszać index (zamiast zwiększania).
cursor_name - nazwa uprzednio zadeklarowanego kursora. W momencie wejścia do pętli FOR kursor jest automatycznie otwierany.
parameter - jeden z parametrów otwarcia kursora (jeśli kursor został zadeklarowany z parametrami).
select_statament - zapytanie związane z wewnętrznym kursorem, niedostępnym dla użytkownika. PL./SQL automatycznie tworzy, otwiera i pobiera dane z kursora (a następnie zamyka go).
Rozkaz EXIT
label_name - opcjonalna nazwa pętli, z której ma nastąpić wyjście. Jeśli nazwa nie jest podana, to rozkaz EXIT powoduje wyjście z najbardziej zagnieżdżonej pętli aktualnie wykonywanej.
plsql_condition - używany w instrukcji EXIT warunkowej. Musi być poprawnym warunkiem języka PL./SQL. Wyjście następuje tylko wtedy, gdy wynikiem obliczenia warunku jest wartość TRUE.
Transakcje
Informacje wstępne o transakcjach
Niepodzielność (Atomicity): Transakcja jest niepodzielną jednostką przetwarzania i może zostać zrealizowana w całości albo nie zrealizowana w ogóle. Realizacja transakcji nie może zakłócić poprawności danych. Przez stan poprawny danych rozumiemy taki stan, w którym wszystkie wartości atrybutów obiektów występujących w bazie mają stan zgodny z oczekiwaniami, tzn. wartość należącą do zbioru wartości danego atrybutu i właściwie odzwierciedlającą stan modelowanej rzeczywistości.
Spójność stanu (Consistency): Poprawne wykonanie transakcji musi przeprowadzić bazę z jednego stanu spójnego w drugi. Stan spójny, to taki, w którym wszelkie powiązania pomiędzy obiektami tworzą logiczną całość tzn. np. nie ma odwołań do obiektów nie istniejących w bazie.
Trwałość (Durability): Niedokończenie transakcji spowodowane błędami środowiska systemowego nie może doprowadzić do uszkodzenia żadnej z baz.
Wyłączność (Isolation): Zmiany wprowadzane przez transakcję do bazy danych nie mogą być widoczne dla innych transakcji aż do momentu ich ostatecznego zatwierdzenia (zrealizowania transakcji w całości).
Szeregowalność (Serializability): Efekt wykonania kilku transakcji jednocześnie (z przełączaniem zadań) musi być równoważny oddzielnemu wykonaniu każdej z nich w pewnej ustalonej kolejności. Wówczas transakcje takie nazywamy szeregowalnymi.
Błąd systemu komputerowego (system crash). Awarie związane ze sprzętem lub oprogramowaniem, zaistniałe podczas wykonywania transakcji. Prawie zawsze związane z utratą zawartości pamięci operacyjnej komputera.
Błąd transakcji lub SZBD. Załamanie wykonania może być spowodowane np. próbą wykonania przez transakcję operacji dzielenia przez zero, przekroczeniem zakresu typu danych, niewłaściwą wartością parametru lub poleceniem BREAK wydanym przez operatora.
Błędy lokalne i wyjątki wykryte przez transakcję. Przykładem okoliczności zmuszających do przerwania transakcji jest np. w bankowej bazie danych, niewystarczający stan konta, uniemożliwiający wykonanie operacji przelewu pieniędzy. Transakcja sama powinna obsłużyć sytuację, wykonując operację ABORT.
Kontrola współbieżności. Procesy bazy odpowiedzialne za kontrolę dostępu równoległego mogą zadecydować o konieczności przerwania transakcji i jej późniejszym restarcie. Przyczyną może być niespełnienie warunku szeregowalności czy też wykrycie stanu zakleszczenia.
Awarie dysku. Błędy zapisu lub odczytu danych z powierzchni dyskowych podczas wykonywania transakcji.
Przyczyny zewnętrzne. Wynikające z zaniku napięcia, przypadkowego lub celowego zamazanie danych przez operatora, pożaru, kradzieży, sabotażu, itp.
Podstawowe strategie jednoczesności
odczytać dane o pożądanych lotach,
sprawdzić czy są wolne miejsca na każdy z tych lotów,
jeśli są, to zarezerwować miejsca na wszystkie kolejne połączenia.
strata zapisanej informacji, np. dla transakcji T1 i T2
odczytanie niepoprawnej informacji w funkcjach agregujących, np. dla transakcji T1 i T3
Teoria szeregowalności
harmonogram sekwencyjny
harmonogram szeregowalny, niesekwencyjny
harmonogram nieszeregowalny, dla którego nie istnieje żaden harmonogram sekwencyjny tego samego zbioru transakcji dający takie same wyniki
pesymistyczna - oparta na blokadzie dostępu do danych,
optymistyczna - oparta na niezależnym wykonaniu transakcji i późniejszym wykrywaniu ewentualnych konfliktów między poszczególnymi transakcjami.
Mechanizm blokad
Blokowanie binarne
gdy transakcja żąda dostępu do obiektu X
gdy transakcja zwalnia blokadę obiektu X
T musi wykonać operację LOCK(X) przed którąkolwiek z operacji READ(X) lub WRITE(X)
T musi wykonać operację UNLOCK(X) po zakończeniu wszystkich operacji READ(X) i WRITE(X)
T nie może wykonać LOCK(X) jeżeli już posiada blokadę X
T nie może wykonać UNLOCK(X) o ile nie wykonała wcześniej LOCK(X)
Blokowanie zapisu i blokowanie aktualizacji
blokadę do czytania -żadna transakcja nie może aktualizować obiektu, który został zamknięty do czytania przez jakąkolwiek transakcję. Natomiast możliwa jest sytuacja, że wiele transakcji czyta dane z tego samego obiektu (dlatego też ten rodzaj nazywany jest trybem dzielonego dostępu do czytania - read-sharable)
blokadę do aktualizacji (blokadę całkowitą) - żadna inna transakcja, z wyjątkiem tej, która nałożyła blokadę nie ma dostępu (zarówno do czytania jak i aktualizacji) do danego obiektu (tryb wyłącznego dostępu do pisania - write-exclusive)
wykonuje operację WRITE_LOCK lub READ_LOCK przed jakąkolwiek operacją READ;
wykonuje operację WRITE_LOCK przed jakąkolwiek operacją WRITE;
nie próbuje odblokować jednostki, której w żaden sposób nie blokuje;
nie próbuje całkowicie zablokować jednostki, którą już w ten sposób blokuje;
nie próbuje zablokować do odczytu jednostki, którą blokuje w jakikolwiek sposób.
Protokół dwufazowy i sprawdzanie szeregowalności
Jeśli transakcja Ti z S blokuje zapis elementu A, a Tj jest następną transakcją (o ile taka istnieje), która chce całkowicie zablokować A, to prowadzimy krawędź Ti Tj.
Jeśli transakcja Ti z S blokuje całkowicie A, a Tj jest następną transakcją (o ile taka istnieje), która chce całkowicie zablokować A, to prowadzimy krawędź Ti Tj.
Jeśli Tm jest transakcją blokującą zapis A po tym, gdy Ti zdjęła swoją całkowitą blokadę lecz zanim Tj całkowicie zablokowała A ( jeśli Tj nie istnieje, to Tm jest dowolną transakcją blokującą zapis A po odblokowaniu jej przez Ti ).
Wyznaczyć wierzchołek, który nie jest końcem żadnej krawędzi (w przeciwnym razie graf zawiera cykle) i wyrzucić go z grafu.
Czy usuneliśmy wszystkie wierzchołki?
jeśli nie to wracamy do punktu 1 algorytmu;
jeśli tak to przechodzimy do punktu 3.
Tworzymy ciąg transakcji według kolejności usuwania z grafu.
Koniec algorytmu.
T5, T3, T2, T4, T1;
T5, T4, T1, T3, T2.
Impas
Zakleszczenie
Transakcja T1 blokuje całkowicie jednostkę A
Transakcja T2 blokuje całkowicie jednostkę B
T1 chce nałożyć blokadę do czytania na jednostkę B, ale musi czekać, bo jest ona zablokowana przez T2
T2 chce nałożyć blokadę do czytania na jednostkę A, ale musi czekać, bo jest ona zablokowana przez T1
Pankowski T., Podstawy baz danych, PWN 1992;
Gruber M. SQL; Helion 1996;
Ullman J.D., Systemy baz danych, WNT 1988;
Flaksiński M., Wstęp do analitycznych metod projektowania systemów informatycznych, WNT 1997;
Jaszkiewicz A., Inżynieria oprogramowania, Helion 1997;
Henderson K., Bazy danych w architekturze klient/serwer, Wydawnictwo Robomatic 1998;
Martin J., Oddel J.,J., Podstawy metod obiektowych,WNT 1997;
Figura D., Obiektowe bazy danych, Akademicka Oficyna Wydawnicza PLJ 1996;
Won Kim, Wprowadzenie do obiektowych baz danych, WNT 1996;
Delobel C., Adiba M., Relacyjne bazy danych, WNT 1989;
Banachowski L., Bazy danych. Tworzenie aplikacji, Akademicka Oficyna Wydawnicza PLJ 1998;
Barker R., Case metod - modelowanie związków encji, 1995;
Barker R., Case metod - modelowanie funkcji i procesów, 1994;
Wrembel R., Wieczerzycki W., Projektowanie aplikacji bazy danych Oracle, PWN 1997;
Cormen T.H., Leiserson C.E., Rivest R.L., Wprowadzenie do algorytmów, WNT 1997;
Austin D., Poznaj Oracle 8, MIKOM 1999;
Przy rozkładach schematów baz danych wykorzystywane są algorytmy rozwiązywania następujących zagadnień:
Algorytmy 4 ,5 i 6 można sprowadzić do algorytmu 3.
Dla danego schematu bazy danych ℜ := { R := ( U, F ) } należy wykonać następujące czynności:
Otrzymany w ten sposób schemat ℜ1 := { Ri := ( Ui , Fi ) | i = 1,2,..,n } jest EQ1-równoważny schematowi ℜ := { R := ( U, F ) } tzn. zachowuje dane i nie musi zachowywać zależności funkcyjnych.
Przykład. Niech ℜ:={R := ( U, F ) }, gdzie U := {Przedmiot, nr_I, Ocena, Sala, Godz_egz, nr_Egzaminatora } i F := { P→GSE, GS→P, PI→O, GI→P }. Stosując metodę dekompozycji otrzymujemy kolejno:
R1 := ( { P, G, S, E }, { P→GSE, GS→P } ) i R2 := ( { P, I, O }, { PI→O } )
będące w 2PN.
R1 := ( { P, G, S, E }, { P→GSE, GS→P } ) i R2 := ( { P, I, O }, { PI→O } )
z kluczami odpowiednio {P,G,S} i {P,I}.
Dla danego schematu bazy danych ℜ := { R := ( U, F ) } należy wykonać następujące czynności:
Przykład. Niech ℜ := { R := ( U, F ) }, gdzie U := { A,B,C,D,X,Y } i F := { XY→A, XY→D, CD→X, CD→Y, AX→B, BY→C, C→A }. Stosując algorytm Bernsteina otrzymujemy kolejno:
F1 = { AX→B }, F2 = { BY→C }, F3 = { C→A },
F4 = { XY→A, XY→D }, F5 = { CD→X, CD→Y }.
J = { XY→CD, CD→XY },
F0 := F0 - { XY→D, CD→X, CD→Y } = { XY→A, AX→B, BY→C, C→A }.
F0' = F0 - { XY→A } = { AX→B, BY→C, C→A }
i odpowiadające im grupy rozpięte nad F0':
F1' = { AX→B }, F2' = { BY→C }, F3' = { C→A }
oraz przy próbie dołączenia zależności z J nową grupę
F4' = { XY→CD, CD→XY }.
ℜ1 := { R1, R2, R3, R4 },
gdzie
R1 := { { A,B,X }, { AX→B } } z kluczem { A,X },
R2 := { { B,C,Y }, { BY→C } } z kluczem { B,Y },
R3 := { { A,C }, { C→A } } z kluczem { C },
R4 := { { C,D,X,Y }, { XY→AD, CD→XY } } z kluczem { X,Y } i { C,D }.
Każdy z otrzymanych schematów jest w 3PN. Schematy ℜ1 i ℜ są EQ2-równoważne.
Przykład. Niech ℜ := { R := ( U, F ) }, gdzie U := { A,B,C,D } i F := { A→B, BC→D, D→BC }. Stosując algorytm Bernsteina otrzymujemy kolejno:
F1 = { A→B }, F2 = { BC→D }, F3 = { D→BC }.
F1 = { A→B }, F2 = { BC→D , D→BC }
oraz
J = { BC→D, D→BC },
F0 := F0 - { BC→D, D→BC } = { A→B }.
F0' = { A→B }.
i odpowiadające im grupy rozpięte nad F0':
F1' = { A→B },
oraz przy próbie dołączenia zależności z J nową grupę
F2' = { BC→D, D→BC }.
ℜ1 := { R1, R2 },
gdzie
R1 := { { A,B }, { A→B } } z kluczem { A },
R2 := { { B,C,D }, { BC→D, D→BC } } z kluczami { B,C } i { D }.
Dla danego schematu bazy danych ℜ := { R := ( U, F ) } należy wykonać następujące czynności:
U' := { A | A należy do zależności funkcyjnej zawartej w F'' }.
Otrzymany w ten sposób schemat ℜ1 := { Ri := ( Ui , Fi ) | i = 1,2,..,n } spełnia następujące warunki:
R = R[U1] ![]()
R[U2] ![]()
... ![]()
R[Un],
Przykład. Niech ℜ := { R := ( U, F ) }, gdzie U := { A,B,C,D } i F := { A→B, BC→D, D→BC }. Stosując algorytm Niekludowej-Calenki otrzymujemy kolejno:
Przykład. Niech ℜ := { R := ( U, F ) }, gdzie U := { A,B,C,D,X,Y } i F := { XY→AD, CD→XY, AX→B, BY→C, C→A }. Stosując algorytm Niekludowej-Calenki otrzymujemy kolejno:
Dla zbioru U' powtarzamy kroki 1 - 4.
Stosujemy algorytm Bernsteina, który daje U2 = {A,X,B} i U = {C,A}.
Końcowy rozkład ma postać:
ℜ1 := { R1, R2, R3 },
gdzie
R1:={{ A,B,X }, { AX→B } } z kluczem { A,X },
R2:={{ A,C }, { C→A } } z kluczem { C },
R3:={{C,D,X,Y,B},{XY→BDC,YBD→XC,CD→XYB}} z kluczami {X,Y},{Y,B,D}, {C,D}.
Otrzymany rozkład różni się od rozkładu otrzymanego przy pomocy algorytmu Bernsteina.
Dane przechowywane są w pamięci zewnętrznej podzielonej logicznie na segmenty składające się z jednostek o stałej długości nazywanej stronami. Każdy plik F(R) rekordów typu R pamiętany jest w jednym segmencie. Spójny obszar pamięci zewnętrznej, w której może być przechowywana jedna strona nazywamy blokiem.
W pamięci operacyjnej wydzielony jest obszar zwany buforem zdolnym do pomieszczenia jednej strony. Przesyłanie danych pomiędzy pamięciami operacyjną i zewnętrzną przedstawia następujący schemat:
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
: |
|
strona |
|
: |
|
|
: |
|
|
|
: |
|
k |
|
|
|
|
: |
|
|
|
|
|
|
: |
|
|
bufory systemowe w pamięci operacyjnej |
|
|
|
|
N |
|
|
|
|
|
bloki w pamięci zewnętrznej |
|
Dla zapamiętania danych można stosować statyczny model pamiętania bazy danych dopuszczający możliwość istnienia spójnych podobszarów, z których składa się obszar pamięci dla segmentu. Dzięki temu istnieje możliwość dynamicznego wzrostu rozmiarów segmentu. Dla każdego segmentu Si, i = 1..p utrzymywana jest specjalna tablica jego podobszarów, która podaje adresy poszczególnych podobszarów oraz liczbę zapamiętanych w nich stron. Model ten można przedstawić przy pomocy następującego schematu:
|
S1 |
S2 |
|
..... |
..... |
|
|
Sp |
|
Podobszar1(S1) |
|
|
podobszar1(Sp) |
|
|
|
|
|
Podobszar1(S2) |
|
|
|
|
|
podobszar2(Sp) |
|
|
|
|
|
podobszar2(S2) |
|
|
|
|
|
Podobszar2(S1) |
|
|
|
|
|
podobszar3(S1) |
|
Dynamiczny model pamiętania bazy danych pozwala każdej stronie w różnych momentach przyporządkować różne bloki w pamięci zewnętrznej co pozwala na zmianę rozmiarów segmentów. W metodzie tej dla każdego segmentu Sk tworzony jest wektor Vk zwany tablicą stron i wektor binarny MAP zawierający tyle pozycji ile bloków istnieje w pamięci zewnętrznej. Model ten można dla dwóch segmentów S1 i S2 przedstawić przy pomocy następującego schematu:
V1 V2
|
3 |
1 |
i |
....... |
0 |
0 |
|
2 |
0 |
j |
....... |
0 |
0 |
segmentów
bloki |
|
|
|
.. |
|
.. |
.. |
|
.. |
|
|
1 |
2 |
3 |
... |
i |
... |
... |
j |
... |
N |
MAP
Wektor binarny określający |
1 |
1 |
1 |
... |
1 |
0 |
0 |
1 |
... |
0 |
zajętość bloków
gdzie wektory V1 i V2 wskazują numery bloków, w których zapamiętane są kolejne strony odpowiednio segmentów S1 i S2, a 1 w wektorze MAP oznacza zajętość odpowiedniego bloku.
Dynamiczny model pamiętania bazy danych pozwala na tzw. przysłanianie pamięci, które polega na zablokowaniu części pamięci na czas konieczny na wykonanie pewnych operacji na zapisanych tam danych. Metoda ta pozwala odtworzyć bazę danych, bez konieczności robienia kopii zapasowej bazy, w przypadku wystąpienia w niej błędów podczas wykonywania operacji na jej danych.
Omówimy model przysłaniania pamięci na przykładzie dwóch segmentów S1 i S2. Realizacja jego wymaga utworzenia dodatkowych wektorów V11, V21, CMAP, które są odpowiednio kopiami wektorów V1, V2, MAP, oraz wektora STATUS, służącego do oznaczenia, że segment S1 lub S2 są zamknięte, tzn. nie jest tworzona jego nowa wersja. Załóżmy, że segment S1 składa się z k stron. Stan bazy danych przed wykonywaniem operacji na zapisanych danych można przedstawić przy pomocy następującego schematu:
V11 V21
tablica stron dla |
|
|
|
....... |
|
|
|
|
|
|
....... |
|
|
segmentów
V1 V2
|
2 |
0 |
0 |
....... |
j |
0 |
|
0 |
4 |
0 |
....... |
N |
0 |
segmentów
bloki |
|
|
|
|
|
.. |
|
.. |
|
|
|
1 |
2 |
3 |
4 |
5 |
... |
j |
... |
N-1 |
N |
MAP STATUS
Wektor binarny określający |
0 |
1 |
0 |
1 |
0 |
... |
1 |
... |
0 |
1 |
|
0 |
0 |
zajętość bloków 1 2
CMAP
Zapasowy wektor binarny |
|
|
|
... |
|
|
|
|
... |
|
określający zajętość bloków
Przy otwieraniu segmentu S1 do operacji zmieniającej jego stan należy:
V11 V21
tablica stron dla |
2 |
0 |
0 |
....... |
j |
0 |
|
|
|
|
....... |
|
|
segmentów
V1 V2
tablica stron dla |
-3 |
-1 |
0 |
....... |
j |
0 |
|
0 |
4 |
0 |
....... |
N |
0 |
segmentów
bloki |
|
|
|
|
|
.. |
|
.. |
|
|
|
1 |
2 |
3 |
4 |
5 |
... |
j |
... |
N-1 |
N |
MAP STATUS
|
0 |
1 |
0 |
1 |
0 |
... |
1 |
... |
0 |
1 |
|
1 |
0 |
CMAP 1 2
|
1 |
1 |
1 |
1 |
0 |
... |
1 |
... |
0 |
1 |
W obydwu przypadkach segment zawiera stan poprawny.
Na każdy rekord należący do pliku F(R):={r1,r2,...,rN} rekordów typu R może być zarezerwowana na stronie stała lub zmienna wielkość pamięci. Niektóre z metod zapisywania rekordów przytoczone są w kolejnym przykładzie.
Przykład. Wystąpienie rekordu typu PRACOWNIK(identyfikator, nazwisko, zawód, płaca, wiek) można zapisać na stronie w następujący sposób:
Długość pola w znakach |
3 |
15 |
15 |
5 |
3 |
|
123 |
Kowalski |
muzyk |
34543 |
23 |
|
123 |
% |
Kowalski |
% |
muzyk |
% |
34543 |
% |
23 |
% |
|
|
|
|
|
|
|
|
123Kowalskimuzyk3454323 |
Na pliku F(R):={r1,r2,...,rN} rekordów typu R mogą być wykonywane następujące czynności:
Dostęp do miejsca zapamiętania w pamięci wystąpienia rekordu można uzyskać np. przy pomocy identyfikatora, którym może być:
Wartość KBD wskazuje jednoznacznie pozycję w pewnej tablicy TIR(R). Pozycja ta zawiera wartość pozwalającą jednoznacznie określić miejsce pamiętania żądanego rekordu. Wartością tą może być:
Wartość KBD rekordu pamiętana jest w obrębie rekordu razem z innymi danymi tego rekordu.
Różne sposoby identyfikacji w pamięci rekordów można zilustrować następująco (przypomnijmy, że na każdej stronie pamiętana jest taka sama ilość rekordów tego samego typu tzn. zajmujących tą samą ilość bajtów):
obszar pamiętania segmentu
|
|
|
|
|
|
|
: |
|
|
1 |
|
|
|
|
|
|
|
: |
|
|
: |
|
adres bezpośredni |
|
|
|
|
|
: |
|
|
: |
|
550 |
|
|
|
|
|
: |
|
|
549 |
|
|
|
|
|
|
|
|
|
|
550 |
|
|
|
|
|
|
|
: |
|
|
551 |
|
|
|
|
|
|
|
: |
|
|
: |
|
|
|
|
|
|
|
: |
|
|
: |
|
|
|
|
|
|
|
: |
|
|
: |
obszar pamiętania segmentu
|
|
|
nr strony |
|
|
|
: |
|
|
|
||||
|
adres pośredni |
|
: |
|
|
|
: |
|
|
17 |
||||
|
550 |
|
: |
549 |
|
|
: |
|
|
|
||||
|
|
|
18 |
550 |
|
|
: |
|
|
|
||||
|
|
|
: |
551 |
|
|
|
|
|
18 |
||||
|
|
|
: |
|
|
|
: |
|
|
|
||||
|
|
|
: |
|
|
|
: |
|
|
|
||||
|
|
|
: |
|
|
|
: |
|
|
: |
||||
|
|
|
: |
|
|
|
: |
|
|
|
||||
|
|
|
|
TIR(R) |
|||||||||||
|
|
|
1 |
: |
strona obliczona z adresu 550 |
||||||||||
KBD = |
R |
3 |
2 |
: |
|
|
|
|
|
|
|||||
|
|
|
3 |
550 |
|
|
|
|
|
|
|||||
|
|
|
4 |
: |
|
|
R |
3 |
|
|
|||||
|
|
|
: |
: |
|
|
|
|
|
|
|||||
|
|
|
: |
: |
|
|
|
|
|
|
|||||
tablica identyfikatorów
rekordów typu R
|
|
|
|
TIR(R) |
|
|||||||||||
|
|
|
1 |
: |
strona numer 18 w segmencie |
|||||||||||
KBD = |
R |
3 |
2 |
: |
|
|
|
|
|
|
||||||
|
|
|
3 |
18 |
|
|
|
|
|
|
||||||
|
|
|
4 |
: |
|
|
R |
3 |
|
|
||||||
|
|
|
: |
: |
|
|
|
|
|
|
||||||
|
|
|
: |
: |
|
|
|
|
|
|
||||||
tablica identyfikatorów
rekordów typu R
Żądany rekord jest znajdowany w wyniku sekwencyjnego przeszukiwania strony.
|
|
|
|
TIR(R) |
|||||||||||
|
|
|
1 |
: |
: |
strona numer 18 w segmencie |
|||||||||
KBD = |
R |
3 |
2 |
: |
: |
|
|
|
|
|
|
|
|||
|
|
|
3 |
18 |
4 |
|
|
|
|
|
|
|
|||
|
|
|
4 |
: |
: |
|
|
R |
3 |
|
|
|
|||
|
|
|
: |
: |
: |
|
|
|
|
|
|
|
|||
|
|
|
: |
: |
: |
|
|
|
|
|
|
|
|||
|
|
|
: |
: |
: |
|
1 |
2 |
3 |
4 |
: |
: |
|||
|
|
|
numer strony |
: |
: |
adres wskaźnika na stronie |
wskaźniki |
||||||||
tablica identyfikatorów
rekordów typu R
Przemieszczenie rekordu w obrębie strony wymaga jedynie aktualizacji odpowiedniego wskaźnika.
W przypadku gdy mamy plik F(R) nieuporządkowany według wartości klucza głównego wyszukiwanie może być realizowane przez kolejne porównywanie wartości klucza głównego wystąpienia rekordu z wartością zadaną. Sposób ten można usprawnić przez przechowywanie wraz z wystąpieniem rekordu dodatkowej informacji o tym, ile razy był wyszukiwany i co pewien czas plik F(R) uporządkować według aktywności poszczególnych wystąpień. Tego typu pliki nazywamy plikami samoorganizującymi się.
Dla pliku F(R) uporządkowanego według wartości klucza głównego (np. w porządku rosnącym) i zapamiętanego kolejno na stronach s1, s2, ... , sm wyszukiwanie rekordu o kluczu głównym x można zrealizować np. według następującego algorytmu:
Graficznie algorytm ten przedstawiony jest na następnym rysunku.
x wartość klucza głównego poszukiwanego rekordu
s1 |
|
|
|
:
si+k |
|
|
|
:
|
|
|
|
:
|
|
Na tej stronie wyszukiwanie rekordu o kluczu x odbywa się sekwencyjnie. |
|
: |
|
|
x |
|
|
: |
|
|
|
|
:
si+k |
|
|
|
:
Omówiony algorytm wyszukiwania można stosować np. do wyszukiwania w plikach indeksowych.
Definicja. Indeksem pliku F(R) nazywamy zbiór
I := { (x,a) | (∃ r∈ F(R) ) (x = key(r) ∧ a = kbd(r) ) },
gdzie key(r) jest wartością klucza głównego w wystąpieniu rekordu r a kbd(r) kluczem bazy danych (adresem) wystąpienia rekordu r. Każdą parę (x,a)∈I nazywamy elementem indeksu.
Definicja. Drzewo T := ( X, K, ω, p) nazywamy drzewem w pełni zrównoważonym gdy długości wszystkich dróg wychodzących z dowolnego wierzchołka do liści są jednakowe.
Definicja. Niech h ≥ 0 i m ≥ 1. Drzewo T nazywamy B-drzewem klasy t(h,m), co zapisujemy T ∈ t(h,m), gdy T = ∅ lub spełnione są następujące warunki:
Wartość h nazywamy wysokością drzewa.
Przykład. Przykład B-drzewa klasy t(3,2)
korzeń
liście
Organizując indeks pliku F(R) w postaci B-drzewa należy każdemu wierzchołkowi przyporządkować jedną stronę danych w następujący sposób:
p0 |
x1 |
a1 |
p1 |
x2 |
a2 |
p2 |
... |
xl |
al |
pl |
|
gdzie
przy czym dla każdego wierzchołka muszą być spełnione następujące warunki:
Wtedy:
Uwaga. Powyższy warunek oznacza, że jeżeli w B-drzewie przeglądać będziemy zbiór wartości klucza głównego wskazywany przez wskaźnik pi-1 leżący na lewo od wartości xi, to w zbiorze tym wszystkie wartości klucza są mniejsze od xi, jeżeli natomiast interesuje nas zbiór wartości klucza głównego wskazywany przez wskaźnik pi leżącego na prawo od wartości xi, to w zbiorze tym znajdziemy wartości większe od xi.
Przykład. Przykład organizacji indeksu w postaci B-drzewa klasy t(3,2) można przedstawić graficznie w następujący sposób:
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
15 |
|
|
|
|
|
|
|
|
|
|
|
35 |
• |
50 |
|
|
|
|
|
|
|
|
|
< |
|
> |
< |
> |
|
|
|
|
|
|
|
|
|
< |
|
> |
< |
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
5 |
• |
7 |
• |
|
|
|
|
|
|
|
• |
32 |
• |
34 |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
12 |
• |
13 |
• |
|
|
|
|
|
|
|
|
• |
36 |
• |
40 |
• |
42 |
• |
45 |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
• |
17 |
• |
20 |
• |
21 |
• |
|
|
|
|
|
|
|
• |
52 |
• |
60 |
• |
|
|
|
|
Dla uproszczenia w wierzchołkach drzewa umieszczono tylko wartości klucza głównego pomijając związane z nim adresy (wartości klucza bazy danych).
Algorytm wyszukiwania. Mamy indeks I zorganizowany w postaci B-drzewa i wartość klucza głównego x. Indeks I jest zapamiętany na stronach. Należy wyznaczyć wartość klucza bazy danych a, takiego że (x,a)∈I lub stwierdzenie, że x nie występuje w indeksie I. Wyszukiwanie realizowane jest według następującego algorytmu:
Zmienna s wskazująca stronę, na której znaleziono dany indeks lub powinien się znajdować, będzie wykorzystywana w następnych algorytmach, których częścią składową będzie algorytm wyszukiwania.
W przypadku, gdy wyszukiwanie zakończyło się niepowodzeniem (w indeksie I brak poszukiwanego elementu ) możliwe jest dołączenie elementu x do indeksu I. Zmienna s wskazuje stronę liścia, do której ma być dołączona para (x,a). Dołączanie to może być bezkolizyjne lub może spowodować przepełnienie strony (tzn. na stronie zapamiętanych jest już 2m elementów indeksu). W pierwszym przypadku element (x,a) dołączany jest w ten sposób by zachować rosnące uporządkowanie wartości klucza głównego na stronie, natomiast w drugim przypadku zastosować należy metodę kompensacji lub podziału.
Algorytm kompensacji. Metodę tę stosujemy wtedy gdy jedna ze stron sąsiadujących ze stroną s zawiera j elementów indeksu, j < 2m. Oznaczmy tą stronę przez s1. Elementy ze stron s i s1 z uwzględnieniem dołączanego elementu (x,a) i elementu (x',a'), dla którego wskażniki po obu stronach wskazują strony s i s1 porządkujemy w ciąg 2m + j +2 elementów. Element "środkowy" (xi,ai), gdzie i := entier( (2m + j +2)/2 ) wstawiamy w miejsce elementu (xi,ai). Strony s i s1 wypełniamy następująco:
Jeżeli s1 leży na prawo od strony s, to elementy (xk,ak), k = 1,2,...,i-1 wstawiamy na stronę s, a elementy (xk,ak), k = i+1,i+2,...,2m+j+2 na stronę s1.
Przykład. Dany jest fragment B-drzewa:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
40 |
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
s1 |
|
|
|
|
|
|
|
|
|
|
• |
20 |
• |
22 |
• |
26 |
• |
34 |
• |
|
|
|
|
|
• |
45 |
• |
50 |
• |
|
|
|
|
Chcemy dołączyć element indeksu o wartości klucza głównego 27. Po uporządkowaniu ciągu wartości klucza głównego otrzymamy ciąg 20,22,26,27,34,40,45,50. Po zastosowaniu metody kompensacji otrzymamy następujący fragment B-drzewa:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
27 |
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
s1 |
|
|
|
|
|
|
|
|
|
|
• |
20 |
• |
22 |
• |
26 |
• |
|
|
|
|
|
|
|
• |
34 |
• |
40 |
• |
45 |
• |
50 |
• |
Algorytm podziału. Niech strona s zawiera 2m elementów. Należy dołączyć element (x,a). W tym celu elementy ze strony s z uwzględnieniem dołączanego elementu (x,a) porządkujemy rosnąco otrzymując ciąg 2m+1 elementów. Elementy o numerach 1,2,...,m umieszczamy na stronie s, a elementy o numerach m+2,m+3,...2m+1 na nowo utworzonej stronie s1. Element (xm+1,am+1) dołączamy do strony będącej wierzchołkiem krawędzi, której końcem jest wierzchołek odpowiadający stronie s w ten sposób, aby wskażnik będący po lewej stronie elementu (xm+1,am+1) wskazywał stronę s, a wskażnik będący po prawej stronie od tego elementu stronę s1. Może się zdarzyć, że strona ta jest zapełniona (zawiera już 2m elementów). Wówczas należy dokonać jej podziału. Może zaistnieć przypadek, że z podziałem dojdziemy aż do korzenia. Przy podziale korzenia istnieje potrzeba utworzenia dwóch nowych stron (wierzchołków) - jeden s1 zgodnie z opisanym już algorytmem oraz strony, która będzie nowym korzeniem B-drzewa. Operacja ta spowoduje powiększenie wysokości B-drzewa.
Algorytm dołączania. Mamy indeks I zorganizowany w postaci B-drzewa oraz element (x,a). Należy element (x,a) dołączyć do indeksu I lub stwierdzić, że element (x,a) już występuje w indeksie I. Dołączanie realizowane jest według następującego algorytmu:
Usuwanie elementu (x,a) z indeksu I jest poprzedzone algorytmem wyszukiwania i ma sens tylko wtedy, gdy poszukiwanie zakończyło się pomyślnie. Wówczas zmienna s wskazuje stronę zawierającą wartość klucza głównego x. Jeżeli strona ta jest liściem to element indeksu o wartości klucza x jest z niej usuwany. Może to spowodować niedomiar, tzn. liczba elementów indeksu na tej stronie może spaść poniżej wartości m. Jeżeli natomiast strona nie jest liściem, to w miejsce usuwanego elementu (x,a) wpisywany jest element o najmniejszej wartości klucza z poddrzewa wskazywanego przez wskaźnik p, stojący po prawej stronie elementu (x,a). Element ten znajdowany jest w wyniku przejścia ścieżką wyznaczoną najpierw przez p, a następnie przez wskaźnik p0 we wszystkich wierzchołkach pośrednich aż do dotarcia do strony liścia, oznaczamy ją symbolem L, i wybrania pierwszego (najmniejszego) elementu tego liścia. Element ten wstawiany jest następnie w miejsce elementu (x,a) i usuwany jest ze strony L. Powyższe operacje nie naruszają w niczym warunków B-drzewa, mogą natomiast spowodować niedomiar na stronie L będącej liściem.
W przypadku wystąpienia niedomiaru stosujemy jedną z metod likwidacji tego niedomiaru, a mianowicie metodę łączenia lub kompensacji.
Algorytm łączenia. Przypuśćmy, że na stronie s, wystąpił niedomiar, tzn. zawiera ona obecnie j elementów, j < m, i jednocześnie jedna z jej stron sąsiednich, oznaczmy ją przez s1, zawiera k elementów i j + k < 2m. Niech s2 oznacza stronę ojca i niech strona s wskazywana będzie przez wskaźnik p, strona s1 przez wskaźnik p', a elementem indeksu między tymi wskaźnikami (xi,ai). Jeżeli s1 leży na prawo od s, to stronę s wypełniamy następująco:
( Jeżeli s1 leży na lewo od s, to role ich się zmieniają i do puli stron wolnych przekazujemy stronę s ).
Usunięcie elementu (xi,ai) ze strony s2 może spowodować niedomiar na tej stronie. Likwidacja tego niedomiaru, (w wyżej opisany sposób ), może spowodować niedomiar na stronie jej ojca, itd. - w skrajnym przypadku aż do korzenia B-drzewa. Może to spowodować zmniejszenie wysokości B-drzewa.
Przykład. W wyniku usunięcia elementu indeksu na stronie s powstał niedomiar
s2
|
|
10 |
p |
20 |
p' |
50 |
|
..... |
s s1
|
12 |
|
|
|
|
..... |
|
|
|
|
24 |
|
28 |
|
|
..... |
|
|
Po operacji łączenia stron s i s1 otrzymamy następujący fragment B-drzewa:
s2
|
..... |
|
|
10 |
|
50 |
|
|
..... |
|
|
s
|
12 |
|
20 |
|
24 |
|
28 |
|
|
..... |
|
Algorytm kompensacji. Przypuśćmy, że na stronie s, wystąpił niedomiar, tzn. zawiera ona obecnie j elementów, j < m, i jednocześnie jedna z jej stron sąsiednich, oznaczmy ją przez s1, zawiera k elementów i j + k 2m. Nie można stosować metody łączenia. Stosuje się wtedy metodę kompensacji. W metodzie tej postępujemy analogicznie jak w metodzie kompensacji przy operacji dołączania elementu indeksu z tym wyjątkiem, że obecnie nie ma potrzeby uwzględniania dodatkowego (dołączanego elementu ). Ponieważ kompensacja przy usuwaniu elementu indeksu nie zmniejsza liczby elementów na stronie ojca, zatem usunięcie niedomiaru na niższym poziomie nie może spowodować powstania niedomiaru na poziomie wyższym (co było możliwe w przypadku stosowania metody łączenia).
Algorytm usuwania. Mamy indeks I zorganizowany w postaci B-drzewa oraz element (x,a). Należy element (x,a) usunąć z indeksu I lub stwierdzić, że element (x,a) już nie występuje w indeksie I. Usuwanie realizowane jest według następującego algorytmu:
Organizując indeks pliku F(R) w postaci B*-drzewa należy każdemu wierzchołkowi B-drzewa klasy t(h*,m*), h* ≥ 2, przyporządkować jedną stronę danych w następujący sposób:
p0 |
x1 |
p1 |
x2 |
p2 |
... |
... |
... |
xl |
pl |
|
|
gdzie
x1 |
a1 |
x2 |
a2 |
x3 |
a3 |
... |
... |
xj |
aj |
|
|
gdzie
przy czym dla każdego wierzchołka muszą być spełnione następujące warunki:
Wtedy:
Przyjmujemy założenie, że wszystkie strony przyporządkowane wierzchołkom są jednakowej długości.W przypadku opisanej organizacji indeksu w postaci B*-drzewa mówimy o organizacji w postaci B*-drzewa klasy t*(h*,m*,m).
Przykład. Przykład organizacji indeksu w postaci B*-drzewa klasy t*(3,2,2) można przedstawić graficznie w następujący sposób:
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ |
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
15 |
|
|
|
|
|
|
|
|
|
|
|
35 |
|
50 |
|
|
|
|
|
|
|
|
|
≤ |
|
> |
≤ |
> |
|
|
|
|
|
|
|
|
|
≤ |
|
> |
≤ |
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
a5 |
10 |
a10 |
|
|
|
|
|
|
|
|
32 |
a32 |
35 |
a35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
a12 |
15 |
a15 |
|
|
|
|
|
|
|
|
|
36 |
a36 |
40 |
a40 |
42 |
a42 |
50 |
a50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
17 |
a17 |
20 |
a20 |
30 |
a30 |
|
|
|
|
|
|
|
|
52 |
a52 |
60 |
a60 |
|
|
|
|
|
W korzeniu i wierzchołkach pośrednich drzewa umieszczamy tylko wartości klucza głównego pomijając związane z nim adresy (wartości klucza bazy danych). W liściach drzewa umieszczamy wartości klucza głównego i związane z nim adresy.
W liściach B*-drzewa umieszczane są w miejsce adresów ai całe rekordy ri odpowiadające kluczowi głównemu xi, przyczym
Przykład. Przykład organizacji pliku rekordów w postaci B*-drzewa klasy t*(3,2,2) można przedstawić graficznie w następujący sposób:
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ |
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
15 |
|
|
|
|
|
|
|
|
|
|
|
35 |
|
50 |
|
|
|
|
|
|
|
|
|
≤ |
|
> |
≤ |
> |
|
|
|
|
|
|
|
|
|
≤ |
|
> |
≤ |
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
r5 |
10 |
r10 |
|
|
|
|
|
|
|
|
32 |
r32 |
35 |
r35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
r12 |
15 |
r15 |
|
|
|
|
|
|
|
|
|
36 |
r36 |
40 |
r40 |
42 |
r42 |
50 |
r50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
17 |
r17 |
20 |
r20 |
30 |
r30 |
|
|
|
|
|
|
|
|
52 |
r52 |
60 |
r60 |
|
|
|
|
|
W korzeniu i wierzchołkach pośrednich drzewa umieszczamy tylko wartości klucza głównego pomijając związrne z nim adresy (wartości klucza bazy danych). W liściach drzewa umieszczamy wartości klucza głównego i związane z nim rekordy.
Dla danego pliku FR rekordów typu R(A1, A2,..., An) i G:={ B1, B2,..., Bk}⊂ {A1, A2,..., An} należy dla x∈DOM(G):=DOM(B1)× DOM(B2)×... ×DOM(Bk) wyznaczyć podzbiór {r∈ FR r(G)=x} zbioru FR.
Możliwe są dwie metody tworzenia ścieżek dostępu do rekordów:
Dla typu rekordów R(A1, A2,..., An) określony jest argument wyszukiwania ![]()
. Rekordy pliku FR pamiętane są w postaci:
... |
A1 |
A2 |
... |
An |
|
|
... |
|
... |
|
|
|
|
|
ścieżki dostępu do argumentów wyszukiwania |
|
|||
Przykład 1. Niech
R(A1, A2, A3, A4):=SAMOCHÓD( NR_REJ, MARKA, KOLOR, ROCZNIK ),
DOM(MARKA)={Fiat, Opel, ...}, DOM(KOLOR)={niebieski, czerwony, zielony,...}.
Argumentami wyszukiwania są {MARKA, KOLOR}. Rekordy są pamiętane w postaci:
SAMOCHÓD(KBD, ... , MARKA, KOLOR, ... , NEXTMARKA, NEXTKOLOR).
Przykład pliku wystąpień rekordów typu SAMOCHÓD ze strukturami łańcuchowymi:
KBD |
|
MARKA |
KOLOR |
|
NEXTMARKA |
NEXTKOLOR |
703 |
... |
Fiat |
Czerwony |
... |
812 |
812 |
|
|
|
: |
|
|
|
805 |
... |
Opel |
Niebieski |
... |
903 |
914 |
|
|
|
: |
|
|
|
812 |
... |
Fiat |
Czerwony |
... |
914 |
903 |
|
|
|
: |
|
|
|
903 |
... |
Opel |
Czerwony |
... |
|
|
|
|
|
: |
|
|
|
914 |
... |
Fiat |
Niebieski |
... |
|
|
|
|
|
: |
|
|
|
Wartość Null atrybutu NEXTMARKA i NEXTKOLOR oznacza, że brak jest następnych rekordów z tą samą wartością atrybutu. W tym przykładzie występuje powiązanie tylko w przód. Można stosować również powiązania w tył (równocześnie).
Przy korzystaniu ze struktur łańcuchowych bardzo ważnym zagadnieniem jest możliwość szybkiego określenia początku łańcucha dla zadanej wartości argumentu wyszukiwania. W tym celu stosuje się indeksy zorganizowane w postaci B-drzewa i B*-drzewa budowane oddzielnie dla każdego argumentu wyszukiwania.
Przykład 2. Organizacja indeksu w celu określenia długości łańcucha (DŁ) i jego początku (PŁ).
Indeks atrybutów (B-drzewo):
|
|
|
|
|
|
MARKA |
|
|
... |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
KOLOR |
|
|
|
... |
|
|
|
|
ROCZNIK |
|
|
|
... |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wskażnik na indeks wartości wskażnik na indeks wartości
atrybutu MARKA atrybutu ROCZNIK
Indeks wartości atrybutów KOLOR, (B*-drzewo).
|
|
|
|
|
|
Niebieski |
|
|
... |
|
|
|
|
|
|||||||||||||
|
|
|
|
≤ |
|
|
> |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Czerwony |
3 |
703 |
niebieski |
2 |
805 |
... |
|
zielony |
DŁ |
PŁ |
... |
||||||||||||||||
Inną metodą jest tzw. hierarchia skorowidzów, w której w obrębie jednego drzewa, którego wierzchołkami są skorowidze zbudowane w specjalny sposób. W metodzie tej wyróżniamy trzy rodzaje skorowidzów:
Wszystkie skorowidze zapamiętywane są na stronach o jednakowej długości i budowa ich jest następująca:
Ad. (1).
SA: |
A1 |
WA1 |
P1 |
A2 |
WA2 |
P2 |
... |
An |
WAn |
Pn |
|
... |
|
|
gdzie
Ai - atrybut (dopuszczalne jest powtarzanie się atrybutu);
WAi - wartość atrybutu, od którego rozpoczyna się strona wskazywana przez Pi;
Pi - wskażnik na stronę skorowidza wartości atrybutu Ai, która rozpoczyna się od
wartości WAi.
Ad. (2).
SWA: |
WA1 |
P1 |
WA2 |
P2 |
... |
WAn |
Pn |
|
... |
|
|
gdzie
WAi - wartość atrybutu, (w jednym skorowidzu zawarte są wartości tylko jednego
atrybutu i są one uporządkowane);
Pi - wskażnik na stronę zawierającą informacje o łańcuchu dla WAi.
Ad. (3).
SPŁ: |
WA1 |
DŁ1 |
PŁ1 |
WA2 |
DŁ2 |
PŁ2 |
... |
WAn |
DŁn |
PŁn |
|
... |
|
|
gdzie
WAi - wartość atrybut;
DŁi - długość łańcucha odpowiadającego WAi;
PŁi - wskażnik na pierwszy rekord w łańcuchu.
Przykład 3.
|
KOLOR |
Czerwony |
|
KOLOR |
zielony |
|
MARKA |
Fiat |
|
... |
SWA: |
Czerwony |
|
niebieski |
|
... |
SWA: |
Zielony |
|
żółty |
|
... |
SPŁ: |
Czerwony |
3 |
703 |
fiolet |
|
|
... |
SPŁ: |
niebieski |
2 |
805 |
popielaty |
|
|
... |
Przypuśćmy, że chcemy wyszukać rekordy typu SAMOCHÓD spełniające warunek
KOLOR="czerwony" i MARKA="Fiat".
Wyszukiwanie przebiega następująco:
W wyniku otrzymujemy rekordy o KBD 703 i 812.
Niech FR={r1, r2,..., rN} będzie plikiem rekordów typu R(A1, A2,..., An), A∈{A1, A2,..., An} i niech x∈DOM(A). Tablicą adresową wartości x atrybutu A w pliku FR nazywamy zbiór
TAF(A,x):={a1, a2,... am}, m≥1,
gdzie ai jest kluczem bazy danych (KBD) rekordu ri∈ FR, w którym atrybut A przyjmuje wartość x.
Przykład. Dla A=KOLOR i x="czerwony" tablica adresowa ma postać TAF(A,x):={703,812,903}.
Takie tablice adresowe tworzone są dla wszystkich wartości tych wszystkich atrybutów, które zostały określone jako argumenty wyszukiwania, (podobnie można określić tablice adresowe dla argumentów wyszukiwania złożonych z kilku atrybutów). Zakładamy, że elementy tablicy adresowej są uporządkowane. Tablice adresowe mogą mieć zmienną długość.
Przykład. Tablice adresowe dla typu rekordów
SAMOCHÓD( NR_REJ, MARKA, KOLOR, ROCZNIK )
o zbiorze wystąpień takim jak w przykładzie 1 z 5.8.2:
Atrybut |
|
Wartość atrybutu |
|
Tablica adresowa |
|
||
A |
|
x |
|
TAF(A,x) |
|
||
|
|
|
|
|
|
||
KOLOR |
|
Czerwony |
|
703 |
812 |
903 |
Suma długości tych tablic jest mniejsza od ilości rekordów w pliku |
|
|
Niebieski |
|
805 |
914 |
|
|
|
|
|
|
|
|
||
MARKA |
|
Fiat |
|
703 |
812 |
914 |
|
|
|
Opel |
|
805 |
903 |
|
|
Jako metodę organizacji dostępu do tablic adresowych można zastosować tzw. hierarchię indeksów lub tzw. hierarchię skorowidzów.
Hierarchia indeksów.
W metodzie tej mamy indeks atrybutów zorganizowany postaci B-drzewa i indeks wartości atrybutów zorganizowany w postaci ![]()
(B*-drzewo o pewnych różnicach na poziomie liści). Liść ![]()
ma następującą postać:
|
DL1 |
INF1 |
... |
IDn |
DLn |
INF1n |
|
INF2n |
|
:
:
INFmn |
|
gdzie
IDi - wartość atrybutu,
DLi - ilość elementów w tablicy adresowej,
INFi - tablica adresowa.
Przykład.
Indeks atrybutów (B-drzewo):
|
|
|
|
|
|
MARKA |
|
|
... |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
KOLOR |
|
|
|
... |
|
|
|
|
ROCZNIK |
|
|
|
... |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wskażnik na indeks wartości wskażnik na indeks wartości
atrybutu MARKA atrybutu ROCZNIK
Indeks wartości atrybutów KOLOR, (![]()
).
|
|
|
|
|
|
Niebieski |
|
|
... |
|
|
|
|
|
|||||||||||
|
|
|
|
≤ |
|
|
> |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Czerwony |
3 |
703 |
812 |
903 |
niebieski |
2 |
805 |
914 |
..... |
||||||||||||||||
Hierarchia skorowidzów.
W metodzie tej wyróżniamy trzy rodzaje skorowidzów:
Wszystkie skorowidze zapamiętywane są na stronach o jednakowej długości i budowa ich jest następująca:
Ad. (1).
SA: |
A1 |
WA1 |
P1 |
A2 |
WA2 |
P2 |
... |
An |
WAn |
Pn |
|
... |
|
|
gdzie
Ai - atrybut (dopuszczalne jest powtarzanie się atrybutu);
WAi - wartość atrybutu, od którego rozpoczyna się strona wskazywana przez Pi;
Pi - wskażnik na stronę skorowidza wartości atrybutu Ai, która rozpoczyna się od
wartości WAi.
Ad. (2).
SWA: |
WA1 |
P1 |
WA2 |
P2 |
... |
WAn |
Pn |
|
... |
|
|
gdzie
WAi - wartość atrybutu, (w jednym skorowidzu zawarte są wartości tylko jednego
atrybutu i są one uporządkowane);
Pi - wskażnik na stronę zawierającą informacje o łańcuchu dla WAi.
Ad. (3).
STA: |
WA1 |
DL1 |
TA1 |
WA2 |
DL2 |
TA2 |
... |
WAn |
DLn |
TAn |
gdzie
WAi - wartość atrybut;
DLi - długość tablicy adresowej;
TAi - tablica adresowa.
Gdy tablica adresowa jest tak długa, że nie mieści się na stronie to pole TAi zostaje rozszerzone do następującej postaci:
|
WAi |
DLi |
ak1 |
|
ak2 |
|
... |
akm |
|
a1 |
a2 |
... |
ak1-1 |
WAi+1 |
... |
|
|
|
|
ak1 |
... |
ak2-1 |
|
ak2 |
... |
ak3-1 |
|
akm |
... |
an |
|
|
|
|
|
przy czym TAi={ a1, a2,..., an}.
Przykład. Dla pliku rekordów z przykładu 1 z 5.8.2 należy wyznaczyć rekordy z warunkiem KOLOR="czerwony" i MARKA="Fiat".
|
KOLOR |
Czerwony |
|
KOLOR |
zielony |
|
MARKA |
Fiat |
|
... |
SWA: |
Czerwony |
|
niebieski |
• |
... |
|
Fiat |
|
Opel |
|
... |
SWA: |
Zielony |
• |
|
|
... |
STA: |
Czerwony |
3 |
703 |
812 |
903 |
... |
STA: |
Fiat |
3 |
703 |
812 |
914 |
... |
W wyniku wyszukiwania otrzymamy {703,812,903}∩{703,812,914}={703,812}.
Definicja. Tablicą binarną dla wartości x atrybutu A pliku FR:={r1, r2,..., rN) nazywamy funkcję
TBF(A,x):{ a1, a2,..., aN)→{0,1}
przy czym
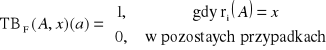
.
|
|
|
703 |
805 |
812 |
903 |
914 |
|
|
|
|
|
|
|
|
|
|
KOLOR |
Czerwony |
|
1 |
0 |
1 |
1 |
0 |
∑1=N |
|
Niebieski |
|
0 |
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
MARKA |
Fiat |
|
1 |
0 |
1 |
0 |
1 |
∑1=N |
|
Opel |
|
0 |
1 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
Dla porównania tablica adresowa ma postać:
KOLOR |
Czerwony |
|
703 |
812 |
903 |
|
Niebieski |
|
805 |
914 |
|
|
|
|
|
||
MARKA |
Fiat |
|
703 |
812 |
914 |
|
Opel |
|
805 |
903 |
|
Jeżeli
N - liczba rekordów w pliku FR,
b - liczba bitów potrzebnych na zapamiętanie jednego elementu z tablicy adresowej,
M - liczba odwracanych atrybutów,
K - ogólna liczba wszystkich wartości odwracanych atrybutów
to
LTA=N*M*b - liczba bitów potrzebna na zapamiętanie wszystkich tablic adresowych,
LMB=N*K - liczba bitów potrzebna na zapamiętanie tablicy binarnej.
Macierz binarna zajmuje mniej miejsca w pamięci, gdy
N*K<N*M*b
tzn. gdy
K<M*b.
Typ |
Opis |
Char(size) |
Ciąg znaków o zmiennej długości nie większej niż podany rozmiar. Dla tego typu maksymalny rozmiar może wynosić 255. W przypadku nie podania rozmiaru domyślnie przyjmowana jest wartość 1 |
Character |
Synonim do char |
Varchar(size) |
W aktualnej wersji ORACLE'a jest to synonim do char, konieczne jest jednak podanie rozmiaru. W przyszłych wersjach zakłada się, że char będzie ciągiem znaków o stałej długości, natomiast varchar o zmiennej. |
Date |
Poprawne daty z zakresu 1 stycznia 4712 p.n.e. do 31 grudnia 4712 n.e. Domyślny format wprowadzania to" DD-MON-YY np.: '01-JAN-89' |
Long |
Ciąg znaków o zmiennej długości nie większej niż 65535 znaków. Można zdefiniować tylko jedną kolumnę typu long w jednej tabeli. |
Long varchar |
synonim do long |
Raw(size) |
Ciąg bajtów o podanej długości. Specyfikacja rozmiaru jest konieczna. Rozmiar maksymalny dla tego typu to 255. Wartości do pól tego typu są wstawiane jako ciągi znaków w notacji szesnastkowej. |
Long raw |
Ciąg bajtów o zmiennej długości. Pozostałe własności jak dla typu long. Wartości do pól tego typu są wstawiane jako ciągi znaków w notacji szesnastkowej. |
Rowid |
Unikalna wartość identyfikująca wiersz. Podany typ jest pseudotypem, tzn. kolumna tego typu nie może być utworzona w tabeli i nie jest w niej przechowywana, ale obliczana na podstawie informacji o fizycznym położeniu wiersza na dysku, w pliku itp. Wartość typu rowid może być przekonwertowana do typu znakowego za pomocą funkcji ROWIDTOCHAR. |
Number |
Typ numeryczny. Jego wartości mogą się zmieniać w zakresie od * 10-129 do 9.99 * 10124. Możliwe jest ograniczenie podanego zakresu przez specyfikację precyzji i skali w sposób opisany poniżej. |
Typ numeryczny jest używany do przechowywania liczb zarówno zmienno jak i stałoprzecinkowych. Dla kolumn numerycznych typ można wyspecyfikować na jeden z trzech sposobów:
number
number (precyzja)
number (precyzja, skala) .
Precyzja określa całkowitą liczbę cyfr znaczących i może się zmieniać od 1 do 38. Skala określa liczbę cyfr po prawej stronie kropki dziesiętnej i może się zmieniać w zakresie od -84 do 127. W momencie definiowania kolumny numerycznej dobrym zwyczajem jest podawanie zarówno precyzji jak i skali, ponieważ wymusza to automatyczną kontrolę wprowadzanych wartości, a więc zwiększa szansę na zachowanie spójności bazy danych. Jeśli wartość przekracza maksymalną precyzję, to generowany jest błąd. Jeśli wartość przekracza skalę, to jest zaokrąglana. Jeśli skala jest ujemna, to wartość jest zaokrąglana do podanej liczby miejsc po lewej stronie kropki dziesiętnej; np. specyfikacja (10, -2) oznacza zaokrąglenie do setek. Czasami specyfikuje się również skalę większą niż precyzję. Oznacza to wtedy, że wprowadzane liczby muszą mieć po kropce dziesiętnej taką liczbę zer jaka jest różnica między skalą a precyzją; np.: number(4, 5) będzie wymagał jednego zera po kropce dziesiętnej. Liczby można również zapisywać w formacie zmiennoprzecinkowym. Składa się ona wtedy z ułamka dziesiętnego, bezpośrednio po którym znajduje się litera E i wykładnik potęgi liczby 10 przez jaki trzeba pomnożyć ten ułamek. Dla przykładu zapis 9.87E-2 oznacza 9.87 * 10-2. Inne systemy baz danych posiadają kilka różnych typów numerycznych, które w ORACLE'u implementowane są jako number. Możliwe jest stosowanie nazw tych typów.
Nazwy te oraz sposób implementacji za pomocą typu number przedstawia tabela:
Specyfikacja |
Typ |
Precyzja |
Skala |
Number |
number |
38 |
null |
Number(*) |
number |
38 |
null |
Number(*, s) |
number |
38 |
s |
Number(p) |
number |
p |
0 |
Number(p,s) |
number |
p |
s |
Decimal |
number |
38 |
0 |
Decimal(*) |
number |
38 |
0 |
Decimal(*, s) |
number |
38 |
s |
Decimal(p) |
number |
p |
0 |
Decimal(p, s) |
number |
p |
s |
Integer |
number |
38 |
0 |
Smallint |
number |
38 |
0 |
Float |
number |
38 |
null |
Float(*) |
number |
38 |
null |
Float(b) |
number |
b |
null |
Real |
number |
63 binary (18 decimal) |
null |
Double |
precision number |
38 |
null |
W systemie zarządzania bazą danych możliwe są konwersje danych jednego typu do danych innego typu. Dane te muszą spełniać pewne warunki, aby konwersja taka była możliwa, np. chcąc przekonwertować ciąg znaków do liczby, ciąg ten powinien składać się z cyfr. Poniższa tabela przedstawia funkcje służące do wykonywania konwersji pomiędzy poszczególnymi typami:
|
Do typu |
||
Z typu |
char |
number |
date |
Char |
zbędna |
TO_NUMBER |
TO_DATE |
Number |
TO_CHAR |
zbędna |
TO_DATE |
Date |
TO_CHAR |
niemożliwa |
zbędna |
Pola tabeli mogą przyjmować wartości puste, pod warunkiem, że nie zostało to zabronione przez projektanta bazy danych. Wartość pusta (NULL) nie jest równa wartości 0 i w wyniku obliczenia dowolnego wyrażenia, którego argumentem jest NULL otrzymuje się również wartość pustą (NULL). Funkcja NVL pozwala dokonać konwersji wartości aktualnej (do niej samej) lub wartości pustej do wartości domyślnej. Działanie funkcji NVL ilustruje przykład: NVL(COMM, 0) zwróci wartość COMM, jeśli nie jest to wartość pusta lub 0 jeśli COMM ma wartość NULL. Większość funkcji grupujących ignoruje wartość NULL. Np. zapytanie, którego zadaniem jest obliczenie średniej z pięciu następujących wartości: 1000, NULL, NULL, NULL i 2000 zwróci 1500 ponieważ (1000 + 2000)/2 = 1500. Jedyne operatory porównania, które można użyć do wartości pustej to IS NULL i IS NOT NULL. Jeśli zostanie użyty jakikolwiek inny operator porównania do wartości pustej, to wynik jest nieokreślony. Ponieważ NULL reprezentuje brak wartości, więc nie może on być równy ani nierówny jakiejkolwiek innej wartości, również innemu NULL. ORACLE traktuje warunki, których wynik jest nieznany jako fałszywe. Tak więc warunek COMM = NULL jest nieznany, w związku z czym rozkaz SELECT z takim warunkiem nie zwróci nigdy żadnego wiersza. Jednak w takiej sytuacji ORACLE nie zgłosi informacji o wystąpieniu błędu.
Poniższa tabela zawiera spis podstawowych rozkazów języka SQL wraz z krótkim opisem. Rozkazy te możemy podzielić na dwie grupy:
Operacje relacyjne będą wyjaśnione dokładniej w dalszej części wykładu.
Rozkaz |
Typ |
Opis |
ALTER TABLE |
DDL |
Dodaje kolumnę do tabeli, redefiniuje kolumnę w istniejącej tabeli lub redefiniuje ilość miejsca zarezerwowaną dla danych |
CREATE INDEX |
DDL |
Tworzy indeks dla tabeli |
CREATE SEQUENCE |
DDL |
Tworzy obiekt służący do generowania kolejnych liczb - sekwencję. Sekwencji można użyć do generowania unikalnych identyfikatorów w tabelach |
CREATE TABLE |
DDL |
Tworzy tabelę i definiuje jej kolumny oraz alokację przestrzeni dla danych |
CREATE VIEW |
DDL |
Definiuje widok dla jednej lub większej ilości tabel lub innych widoków |
DELETE |
DML |
Usuwa wszystkie lub wyróżnione wiersze z tabeli |
DROP obiekt |
DDL |
Usuwa indeks, sekwencje, tablicę, widok lub inny obiekt |
INSERT |
DML |
Dodaje nowy wiersz (lub wiersze) do tabeli lub widoku |
RENAME |
DDL |
Zmienia nazwę tabeli, widoku lub innego obiektu |
SELECT |
DML |
Wykonuje zapytanie. Wybiera wiersze i kolumny z jednej lub kilku tabel |
UPDATE |
DML |
Zmienia dane w tabeli |
COMMIT |
DCL |
Kończy transakcję i na stałe zapisuje zmiany |
ROLLBACK |
DCL |
Wycofuje zmiany od początku transakcji lub zaznaczonego punktu. |
SAVEPOINT |
DCL |
Zaznacza punkt, do którego możliwe jest wykonanie rozkazu ROLLBACK |
SET TRANSACTION |
DCL |
Zaznacza aktualną transakcję jako read-only (tylko do odczytu). |
Identyfikator (nazwa) - ciąg liter, cyfr i znaków podkreślenia rozpoczynający się literą lub znakiem podkreślenia. Różne systemy baz danych umożliwiają stosowanie innych znaków wewnątrz identyfikatorów (np. znak '$', lub '!'). Stosowanie tych znaków nie jest jednak zalecane ze względu na późniejsze problemy związane z przenośnością napisanych w ten sposób aplikacji.
Słowa zarezerwowane - identyfikatory zastrzeżone posiadające specjalne znaczenie w języku SQL. Spis wszystkich słów zarezerwowanych w języku SQL przez twórców ORACLE'a przedstawia tabela:
access
add
all
alter
and
any
as
asc
audit
between
by
char
check
cluster
column
comment
compress
connect
create
current
date
dba
decimal
default
delete
desc
distinct
drop
else
exclusive
exists
file
float
for
from
grant
graphic
group
having
identified
if
immediate
in
increment
index
install initialinsert
integer
intersect
into
is
level
like
lock
long
max
extents
minus
mode
modify
noaudit
nocompress
notnowait
null
number
of
offline
on
online
option
or
order
pctfree
prior
privileges
publicraw
rename
resource
revoke
row
rowid
rownum
row
sselect
session
set
share
size
smallint
start
successful
synonym
sysdate
table
then
to
trigger
uid
union
unique
update
user
validate
values
varchar
var
graphic
view
when
ever
where
with
Liczby - mogą być całkowite lub rzeczywiste. Liczba całkowita nie posiada kropki dziesiętnej. W systemie ORACLE liczby można zapisywać w formacie zwykłym lub wykładniczym. Format wykładniczy składa się z liczby oraz wykładnika liczby 10, przez który należy pomnożyć tę liczbę oddzielonego literą 'e' lub 'E'.
Przykłady.
Dodatkowo w systemie ORACLE liczbę całkowitą można zakończyć literą 'K' lub literą 'M'. Litera 'K' oznacza, że cała liczba ma być pomnożona przez 1024 (1 KB), natomiast litera 'M', że liczbę należy pomnożyć przez 1048576 (1 MB).
Przykłady.
Rozkazy języka SQL kończą się średnikiem.
Rozkaz CREATE TABLE służy do tworzenia struktury tabeli (bez danych) i posiada dodatkowe opcje umożliwiające:
Rozkaz CREATE TABLE posiada następującą składnię:
CREATE TABLE [user.]table ( {column_element | table_constraint}
[, {column_element | table_constraint} ] ... )
[ PCTFREE n ] [ PCTUSED n ]
[ INITTRANS n ] [ MAXTRANS n ]
[ TABLESPACE tablespace ]
[ STORAGE storage ]
[ CLUSTER cluster (column [, column] ...) ]
[ AS query ];
Parametry:
Przykład.
CREATE TABLE pracownicy
( nr_pracownika NUMBER NOT NULL PRIMARY KEY,
imie CHAR(15) NOT NULL CHECK (imie = UPPER(imie)),
nazwisko CHAR(25) NOT NULL CHECK (nazwisko = UPPER(nazwisko)),
nr_wydzialu NUMBER (3) NOT NULL );
Rozkaz drop służy do kasowania obiektów różnego rodzaju. Ogólna postać tego rozkazu jest następująca:
DROP object_type [user.]object
Poniżej przedstawione są różne postacie rozkazu drop służące do kasowania poszczególnych typów obiektów:
Rozkaz insert dodaje nowe wiersze do tabeli lub do tabel przynależących do widoku. Aby dodać wiersze do tabeli należy być właścicielem tabeli, administratorem (DBA) lub posiadać uprawnienia dopisywania do tej tabeli.
Składnia rozkazu:
INSERT INTO [user.]table [ (column [, column] ...) ]
{ VALUES (value [, value] ...) | query };
Parametry:
Opis:
Rozkaz INSERT użyty z klauzulą VALUES zawsze dodaje dokładnie jeden wiersz. Do pól wyspecyfikowanych w liście kolumn (lub do wszystkich kolumn) wstawiane są podane wartości. Kolumny nie wyspecyfikowane na liście kolumn przyjmują wartości puste NULL (w związku z tym nie mogą być uprzednio zadeklarowane jako NOT NULL).
Jeśli użyje się rozkazu SELECT zamiast klauzuli VALUES, to możliwe jest dodanie większej ilości wierszy (wszystkich zwróconych przez zapytanie). Po wykonaniu zapytania kolumny będące jego rezultatem są dopasowywane i wpisywane do kolumn podanych na liście kolumn (lub do wszystkich kolumn, jeśli ich nie wyspecyfikowano). Zapytanie może odwoływać się również do tabeli, do której
dopisywane są wiersze.
W przypadku, gdy lista kolumn nie jest podana, to wartości są dopasowywane do poszczególnych kolumn na podstawie ich wewnętrznego porządku. Porządek ten nie musi być taki sam jak kolejność kolumn przy tworzeniu tabeli. Żaden wiersz nie zostanie dopisany, jeśli zapytanie nie zwróci żadnych wierszy.
Przykłady.
VALUES (50, 'JAN', 'KOWALSKI', 3);
SELECT 'Pan Tadeusz', autor_nr, miejsce_nr
FROM autorzy, miejsca
WHERE nazwisko = 'Mickiewicz' AND miejsce = 'lewa polka' ;
Rozkaz DELETE służy do usuwania wierszy z tabeli.
Składnia:
DELETE [FROM] [user.]table [alias] [WHERE condition] ;
Parametry:
Opis:
Cała przestrzeń zwolniona przez skasowane wiersze i elementy indeksów jest zatrzymywana przez tę tabelę i indeks.
Przykłady:
DELETE FROM pracownicy ;
DELETE FROM ksiazki WHERE autor = 2 ;
Tworzy obiekt (nazywany sekwencją), za pomocą którego wielu użytkowników może generować unikalne liczby całkowite. Sekwencję mogą być użyte do generacji kluczy pierwotnych w sposób automatyczny. Do utworzenia sekwencji konieczne są przynajmniej uprawnienia RESOURCE w co najmniej jednej przestrzeni tabel.
Składnia:
CREATE SEQUENCE [user.]sequence
[INCREMENT BY n]
[START WITH n]
[MAXVALUE n | NOMAXVALUE]
[MINVALUE n | NOMINVALUE]
[CYCLE | NOCYCLE]
[CACHE n | NOCACHE]
[ORDER | NOORDER];
Parametry:
Opis:
Sekwencje mogą być używane do generacji kluczy pierwotnych dla jednej tabeli lub wielu tabel i wielu użytkowników. Aby mieć dostęp do sekwencji, której właścicielem jest inny użytkownik, należy mieć uprawnienia SELECT do tej sekwencji. Sekwencja może posiadać synonim. Numery w sekwencjach są generowane niezależnie od tabel, dlatego mogą być używane jako liczby unikalne dla kilku różnych tabel i użytkowników. Jest jednak możliwe, że niektóre numery z sekwencji zostaną pominięte, ponieważ zostały one wygenerowane i użyte w transakcji, która następnie została wycofana. Dodatkowo jeden użytkownik może nie zdawać sobie sprawy, że inni użytkownicy korzystają z tej samej sekwencji (co również skutkuje pominięciem numerów dla tego użytkownika). Dostęp do sekwencji zapewniają dwie pseudokolumny: NEXTVAL i CURRVAL. Pseudokolumna NEXTVAL jest używana do generacji następnej wartości z podanej sekwencji.
Składnia jest następująca:
sequence.NEXTVAL
gdzie sequence jest nazwą sekwencji.
Pseudokolumna CURRVAL pozwala na odczytanie aktualnej wartości sekwencji. Aby możliwe było użycie CURRVAL konieczne jest wcześniejsze użycie NEXTVAL w aktualnej sesji dla danej sekwencji.
Składnia jest następująca:
sequence.CURRVAL
gdzie sequence jest nazwą sekwencji. Pseudokolumny NEXTVAL i CURRVAL mogą być używane w:
Pseudokolumn NEXTVAL i CURRVAL nie można używać w: podzapytaniach w liście select dla widoków ze słowem kluczowym DISTINCT z klauzulami ORDER BY, GROUP BY i HAVING w rozkazie SELECT z operatorem ustawienia (UNION, INTERSECT, MINUS)
Przykład.
CREATE SEQUENCE eseq INCREMENT BY 10;
INSERT INTO pracownicy
VALUES (eseq.NEXTVAL, 'Jan', 'Kowalski', 3);
Rozkaz SELECT służy do wyświetlania wierszy i kolumn z jednej lub kilku tabel. Może być używany jako osobny rozkaz lub (z pewnymi ograniczeniami) jako zapytanie lub podzapytanie w innych poleceniach. Aby odczytać dane z określonej tabeli trzeba być jej właścicielem, mieć uprawnienia SELECT dla tej tabeli lub być administratorem bazy (DBA).
Składnia:
SELECT [ALL | DISTINCT]
{* | table.* | expr [c_alias] }
[, { table.* | expr [c_alias] } ] ...
FROM [user.]table [t_alias]
[, [user.]table [t_alias]] ...
[ WHERE condition ]
[ CONNECT BY condition [START WITH condition] ]
[ GROUP BY expr [. Expr] ... [HAVING condition] ]
[ {UNION | INTERSECT | MINUS} SELECT ...]
[ ORDER BY {expr | position} [ASC | DESC]
[, {expr | position} [ASC | DESC]] ] ...
[ FOR UPDATE OF column [, column] ... [NOWAIT] ];
Parametry:
Opis:
Użycie nazwy tabeli przed nazwą kolumny i nazwy użytkownika przed nazwą tabeli jest najczęściej opcjonalne, to jednak dobrym zwyczajem jest podawanie nazw w pełni kwalifikowanych z dwóch powodów:
Pozostałe operacje wykonywane przez rozkaz SELECT zostaną opisane w dalszej części wykładu.
Przykłady.
FROM ksiazki, autorzy, miejsca
WHERE ksiazki.autor = autorzy.autor_nr AND ksiazki.miejsce = miejsca.miejsce_nr ;
Rozkaz UPDATE służy do zmiany danych zapisanych w tabeli. Warunkiem wykonania tego polecenia jest bycie właścicielem tabeli, administratorem (DBA) lub posiadanie uprawnień UPDATE dla tej tabeli.
Składnia:
UPDATE [user.]table [alias]
SET column = expr [, column = expr] ...
[ WHERE condition ];
lub
UPDATE [user.]table [alias]
SET (column [, column] ...) = (query)
[, column [, column] ...) = (query) ] ...
[ WHERE condition ];
Parametry:
Warunki będą opisane w dalszej części wykładu
Opis:
Klauzula SET określa, które kolumny zostaną zmienione i jakie nowe wartości mają być w nich zapisane. Klauzula WHERE określa warunki jakie muszą spełniać wiersze, w których należy wymienić wartości podanych wcześniej kolumn. Jeśli klauzula WHERE nie jest podana, to zmieniane są wszystkie wiersze w tabeli. Rozkaz UPDATE dla każdego wiersza, który spełnia warunki klauzuli WHERE oblicza wartości wyrażeń znajdujących się po prawej stronie operatora '=' i przypisuje te wartości do pola określanego przez nazwę kolumny z lewej strony. Jeśli klauzula SET posiada podzapytanie, to musi ono zwrócić dokładnie jeden wiersz dla każdego ze zmienianych wierszy. Każda wartość jest przypisywana zgodnie z kolejnością na liście kolumn. Jeśli zapytanie (w przypadku klauzuli postaci SET value = query) nie zwróci wierszy to odpowiednie pola są ustawiane na NULL.
Zapytanie może odwoływać się do zmienianej tabeli. Jest ono obliczane oddzielnie dla każdego zmienianego wiersza a nie dla całego rozkazu UPDATE.
Przykład.
UPDATE pracownicy
SET nr_wydziału = 4
WHERE nr_wydziału = 3 ;
Rozkaz RENAME zmienia nazwę tabeli, widoku lub synonimu. Zmiany może dokonać właściciel tabeli, widoku lub synonimu.
Składnia:
RENAME old TO new
Parametry:
Opis:
Wszystkie pozwolenia, które posiadał obiekt o starej nazwie, przechodzą na obiekt o nowej nazwie. Za pomocą tego rozkazu nie można zmieniać nazw kolumn. Zmiana nazwy kolumny może być dokonana za pomocą trzech rozkazów: CREATE TABLE, DROP TABLE i RENAME w następujący sposób:
CREATE TABLE temporary (new_column_name)
AS SELECT old_column_name FROM table ;
DROP TABLE table ;
RENAME temporary TO table ;
Przykład.
RENAME wydzialy TO jednostki ;
Rozkaz tworzy nowy indeks dla tabeli lub klastra. Indeks zapewnia bezpośredni dostęp do wierszy w tabeli w celu zredukowania czasu wykonywania operacji. Indeks zawiera informację o każdej wartości, która jest zapisana w indeksowanej kolumnie. Indeks może utworzyć właściciel tabeli, użytkownik posiadający uprawnienia INDEX dla danej tabeli lub administrator (DBA).
Składnia:
CREATE [UNIQUE] INDEX index ON
{table(column [ASC|DESC][, column [ASC|DESC]]...) |
CLUSTER cluster}
[INITTRANS n] [MAXTRANS n]
[TABLESPACE tablespace]
[STORAGE storage]
[PCTFREE n]
[NOSORT];
Parametry:
Opis:
Indeksy są tworzone w celu przyspieszenia operacji: dostępu do danych w posortowanych według kolumn indeksowanych wyszukiwania wierszy, zawierających dane z indeksowanych kolumn. Należy jednak zwrócić uwagę, że indeks spowalnia wstawianie, usuwanie i zmiany wartości w indeksowanych kolumnach, ponieważ jego zawartość musi ulec zmianie w momencie zmiany zawartości tabeli. Do jednego indeksu wstawionych może być co najwyżej 16 kolumn. Jeden element indeksu jest konkatenacją wartości tych kolumn w poszczególnych wierszach. W momencie wyszukiwania może być użyty cały element indeksu lub pewna jego część początkowa. Dlatego kolejność kolumn w indeksie jest ważna. Jeśli więc indeks zostanie utworzony na podstawie trzech kolumn A, B, C w takiej kolejności, to zostanie on użyty do wyszukiwania konkatenacji kolumn A, B, C, kolumn A i B lub tylko kolumny A. Nie będzie natomiast używany w przypadku wyszukiwania połączenia kolumn B i C lub pojedynczej kolumny B lub C. Możliwe jest utworzenie dowolnej ilości indeksów dla jednej lub kilku tabel. Należy jednak pamiętać, że oprócz spowolnienia operacji modyfikacji tabeli, indeksy zajmują również dość dużą ilość miejsca na dysku.
Przykład.
CREATE INDEX i_prac_imie ON pracownicy (imie) ;
Rozkaz służący do tworzenia widoku, czyli logicznej tabeli bazującej na jednej lub wielu tabelach. Utworzyć widok może właściciel tabel, użytkownik posiadający do nich co najmniej uprawnienia SELECT lub administrator.
Składnia:
CREATE VIEW [user.]view [(alias [, alias] ...)]
AS query
[ WITH CHECK OPTION [CONSTRAINT constraint] ] ;
Parametry:
Opis:
Widok jest logicznym oknem dla jednej lub kilku tabel. Widok ma następujące właściwości:
Możliwa jest zmiana danych zawartych w widoku, który posiada pseudokolumny lub wyrażenia dotąd dopóki rozkaz UPDATE nie odwołuje się do pseudokolumny lub wyrażenia.
Widoki są używane do:
Przykład.
CREATE VIEW bibl
AS SELECT ksiazki.tytul, autorzy.imie, autorzy.nazwisko, miejsca.miejsce
FROM ksiazki, autorzy, miejsca
WHERE ksiazki.autor = autorzy.autor_nr AND ksiazki.miejsce = miejsca.miejsce_nr
WITH CHECK OPTION CONSTRAINT chkopt ;
Składnia:
COMMIT [WORK];
Opis:
Rozkaz COMMIT i COMMIT WORK wykonują tę samą operację polegającą na zakończeniu aktualnej transakcji i stałym zapisaniu wszystkich dokonanych zmian w bazie danych.
Składnia:
ROLLBACK [ WORK ] [TO [ SAVEPOINT ] savepoint ];
Parametry:
Opis:
Rozkaz ROLLBACK wycofuje wszystkie zmiany aż do podanego punktu (w przypadku klauzuli TO) lub początku transakcji (bez klauzuli TO).
Przykłady.
Składnia:
SAVEPOINT savepoint;
Parametry:
Opis:
Rozkaz SAVEPOINT jest używany w połączeniu z ROLLBACK do wycofywania fragmentów wykonywanej transakcji. Nazwy punktów muszą być unikalne w jednej transakcji. Systemy zarządzania bazami danych wprowadzają najczęściej ograniczenia na liczbę punktów, które można zaznaczyć w jednej transakcji.
Przykłady.
SET placa_podstawowa = 2000
WHERE nazwisko = 'Kowalski' ;
SAVEPOINT Kow_plac;
SET placa_podstawowa = 1500
WHERE nazwisko = 'Nowak' ;
SAVEPOINT Now_plac;
ROLLBACK TO SAVEPOINT Kow_plac;
SET placa_podstawowa = 1300
WHERE nazwisko = 'Nowak' ;
COMMIT;
Składnia:
SET TRANSACTION { READ ONLY };
Parametry:
Opis:
Rozkaz informuje system, że wykonywana transakcja będzie składać się tylko z zapytań. Nie jest możliwe używanie w takiej transakcji rozkazów INSERT, UPDATE lub DELETE. Rozkaz SET TRANSACTION musi wystąpić jako pierwszy w transakcji, w przeciwnym razie zgłoszony zostanie błąd.
Operacja selekcji umożliwia pobranie krotek (wierszy) spełniających określony warunek. Operacja ta nazywana jest również podzbiorem poziomym.
W języku SQL wykonanie selekcji umożliwia rozkaz SELECT z klauzulą WHERE. Przykładowo polecenie:
SELECT * FROM osoby;
spowoduje wybranie wszystkich krotek (wierszy) z relacji (tabeli) ludzie. W celu pobrania wierszy, dla których pole w kolumnie 'Wykształcenie' jest równe 'SO' (średnie ogólne) należy napisać:
SELECT * FROM osoby
WHERE Wykształcenie = 'SO' ;
Warunki selekcji mogą być złożone. Przykładowo, aby wybrać wszystkie osoby, które mają wykształcenie średnie (średnie techniczne - ST lub średnie ogólne - SO) można odpowiednie warunki połączyć spójnikiem logicznym OR, czyli zapisać w następujący sposób:
SELECT * FROM osoby
WHERE Wykształcenie = 'ST' OR Wykształcenie = 'SO' ;
Budowa wyrażeń i warunków zostanie opisana dokładniej w dalszej części wykładu.
Projekcja umożliwia pobranie wartości wybranych atrybutów, wymienionych po słowie kluczowym SELECT z wszystkich krotek relacji. Operacja ta jest nazywana także podzbiorem pionowym.
Przykładową operację projekcji pokazaną na rysunku można wykonać za pomocą następującego rozkazu SELECT:
SELECT Pesel, Wykształcenie FROM osoby ;
Operacje selekcji i projekcji mogą być łączone w jednym rozkazie SELECT. I tak chcąc otrzymać kolumny zawierające Pesel i Nazwisko osób mających średnie wykształcenie należy napisać:
SELECT Pesel, Nazwisko FROM osoby
WHERE Wykształcenie = 'ST' OR Wykształcenie = 'SO' ;
Produkt (iloczyn kartezjański) jest operacją teorii zbiorów. Operacja ta umożliwia łączenie dwóch lub więcej relacji w taki sposób, że każda krotka pierwszej relacji, jest łączona z każdą krotką drugiej relacji. W przypadku większej ilości relacji, operacja ta jest wykonywana, na pierwszych dwóch, a następnie na otrzymanym wyniku i relacji następnej, aż do wyczerpania wszystkich argumentów. Przykładowe wykonanie iloczynu kartezjańskiego przedstawia rysunek.
Znajdowanie iloczynu kartezjańskiego dwóch relacji (tabel) jest również wykonywane przez rozkaz SELECT. Przedstawioną na rysunku operację można wykonać za pomocą następującego rozkazu:
SELECT * FROM R1, R2;
Operacja znajdowania iloczynu kartezjańskiego może być łączona zarówno z operacją selekcji, jak również projekcji lub oboma równocześnie.
Operacja ta polega na łączeniu krotek dwóch lub więcej relacji z zastosowaniem określonego warunku łączenia. Wynikiem połączenia jest podzbiór produktu relacji.
Operację można wykonać następującym poleceniem SELECT:
SELECT imie, nazwisko, tytul
FROM autorzy, ksiazki
WHERE autorzy.nazwisko = 'Mickiewicz' AND autorzy.nr = ksiazki.autor ;
Wyrażenie jest ciągiem jednej lub więcej wartości, operatorów lub funkcji. Wynik obliczania wyrażenia musi być wartością. W ogólności typ wyniku zależy od typów operandów.
Następujące przykłady pokazują wyrażenia różnych typów:
numeryczny: 2 * 2
znakowy: TO_CHAR(TRUNC(SYSDATE + 7))
Wyrażenie może być użyte wszędzie tam, gdzie możliwe jest użycie wartości stałej, np.:
SET Nazwisko = LOWER(Nazwisko)
Istnieje pięć form wyrażeń:
Składnia:
Przykłady.
Składnia:
: { n | variable } [ :ind_variable ]
Przykłady.
Składnia:
function_name( [DISTINCT | ALL] expr [, expr] ... )
Przykłady.
Składnia:
Przykłady.
Składnia:
(expr [, expr], ...)
Przykłady.
Wyrażenia są używane w:
Warunkiem nazywamy ciąg jednego lub więcej wyrażeń i operatorów logicznych. Warunek jest zawsze obliczany do wartości TRUE lub FALSE. Warunki mogą mieć siedem różnych postaci:
<expr> [NOT] BETWEEN <expr> AND <expr>
<expr> IS [NOT] NULL
EXISTS <query>
Przykłady.
Składnia:
Funkcja |
Przeznaczenie |
Przykład |
ABS(n) |
Zwraca wartość absolutną liczby n |
ABS(-15). Wynik: 15 |
CEIL(n) |
Zwraca najmniejszą liczbę całkowitą większą lub równą n. |
CEIL(15.7). Wynik: 16 |
FLOOR(n) |
Zwraca największą liczbę całkowitą mniejszą lub równą n. |
FLOOR(15.7). Wynik: 15 |
MOD(m, n) |
Zwraca resztę z dzielenia liczby m przez n |
MOD(7, 5). Wynik: 2 |
POWER(m, n) |
Zwraca liczbę m podniesioną do potęgi n. Liczba n musi być całkowita; w przeciwnym wypadku wystąpi błąd. |
POWER(2, 3). Wynik: 8 |
ROUND(n[, m]) |
Zwraca liczbę n zaokrągloną do m miejsc po przecinku. Jeśli m jest pominięte, to przyjmuje się 0. Liczba m może być dodatnia lub ujemna (zaokrąglenie do odpowiedniej liczby cyfr przed przecinkiem) |
Wynik: 16.2, Wynik: 20 |
SIGN(n) |
Zwraca 0, jeśli n jest równe 0, -1 jeśli n jest mniejsze od 0, 1 jeśli n jest większe od 0 |
SIGN(-15) Wynik: -1 |
SQRT(n) |
Zwraca pierwiastek kwadratowy liczby n. Jeśli n<0 to wystąpi błąd |
SQRT(25). Wynik: 5 |
TRUNC(m[, n]) |
Zwraca m obcięte do n miejsc po przecinku. Jeśli n nie jest podane, to przyjmuje się 0. Jeśli n jest ujemne to obcinane są cyfry przed przecinkiem. |
Składnia:
Składnia |
Przeznaczenie |
Przykład |
CHR(n) |
Zwraca znak o podanym kodzie |
CHR(65) Wynik: "A" |
INITCAP(string) |
Zwraca string, w którym każde słowo ma dużą pierwszą literę, a pozostałe są małe. |
INITCAP('PAN JAN NOWAK') Wynik: "Pan Jan Nowak" |
LOWER(string) |
Zamienia wszystkie litery w podanym stringu na małe. |
LOWER('PAN JAN NOWAK') Wynik: "pan jan nowak" |
LPAD(string1, n [, string2]) |
Zwraca string 1 uzupełniony do długości n lewostronnie ciągami znaków ze stringu 2. Jeśli string2 nie jest podany to przyjmowana jest spacja. Jeśli n jest mniejsze od długości string1, to zwracane jest n pierwszych znaków z tekstu string1. |
LPAD('Ala ma ', kota*, 17) Wynik: "kota*kota*Ala ma " |
LTRIM(string [, zbiór]) |
Usuwa litery z tekstu string od lewej strony aż do napotkania litery nie należącej do tekstu zbiór. Jeśli zbiór nie jest podany to przyjmowany jest ciąg pusty. |
LTRIM('xxxXxxOstatnie słowo', 'x') Wynik: "XxxOstatnie słowo" |
REPLACE(string, search [, replace]) |
Zwraca string z zamienionym każdym wystąpieniem tekstu search na tekst replace. |
REPLACE('Jack & Jue', 'J', Bl') Wynik: "Black & Blue" |
RPAD(string1, n [, string2]) |
Zwraca string 1 uzupełniony prawostronnie do długości n ciągami string2. Jeśli string2 nie jest podany, to przyjmuje się spację, Jeśli n jest mniejsze od długości string1, to zwracane jest n pierwszych znaków z tekstu string1. |
RPAD('Ala ma ', 17, 'kota*') Wynik: "Ala ma kota*kota*" |
RTRIM(string [, zbiór]) |
Zwraca string1 z usuniętymi ostatnimi literami, które znajdują się w stringu zbiór. Jeśli zbiór nie jest podany to przyjmowany jest ciąg pusty |
RTRIM('Ostatnie słowoxxXxxx', 'x') Wynik: "Ostatnie słowoxxX" |
SOUNDEX(string) |
Zwraca ciąg znaków reprezentujący wymowę słów wchodzących w skład string1. Funkcja SOUNDEX może być użyta do porównywania słów zapisywanych w różny sposób, ale wymawianych tak samo. |
SELECT nazwisko FROM bibl WHERE SOUNDEX(nazwisko) = SOUNDEX('Mickiewicz'); |
SUBSTR(string, m [, n]) |
Zwraca podciąg z ciągu znaków string zaczynający się na znaku m i o długości n. Jeśli n nie jest podane, to zwracany jest podciąg od znaku m do ostatniego w string. Pierwszy znak w ciągu ma numer 1. |
SUBSTR('ABCDE',2, 3) Wynik: "BCD" |
TRANSLATE( string, from, to) |
Zwraca string powstały po zamianie wszystkich znaków from na znak to. |
TRANSLATE( 'HELLO! THERE!', '!', '-') Wynik: "HELLO- THERE-" |
UPPER(string) |
Zamienia wszystkie znaki z ciągu string na duże litery. |
UPPER('Jan Nowak') Wynik: "JAN NOWAK" |
ASCII(string) |
Zwraca kod ASCII pierwszej litery w podanym ciągu znaków |
ASCII('A') Wynik: 65 |
INSTR(string1, string2 [, n [, m]]) |
Zwraca pozycję m-tego wystąpienia string2 w string1, jeśli szukanie rozpoczęto od pozycji n. Jeżeli m jest pominięte, to przyjmowana jest wartość 1. Jeśli n jest pominięte, przyjmowana jest wartość 1. |
INSTR( 'MISSISSIPPI', 'S', 5, 2) Wynik: 7 |
LENGTH(string) |
Zwraca długość podanego ciągu znaków. |
LENGTH('Nowak') Wynik: 5 |
Funkcje grupowe zwracają swoje rezultaty na podstawie grupy wierszy a nie pojedynczych wartości. Domyślnie cały wynik jest traktowany jako jedna grupa. Klauzula GROUP BY z rozkazu SELECT może jednak podzielić wiersze wynikowe na grupy. Klauzula DISTINCT wybiera z grupy tylko pojedyncze wartości (drugie i następne są pomijane). Klauzula ALL powoduje wybranie wszystkich wierszy wynikowych do obliczenia wyniku. Wszystkie wymienione w tym podrozdziale funkcje opuszczają wartości NULL z wyjątkiem COUNT(*). Wyrażenia będące argumentami funkcji mogą być typu CHAR, NUMBER lub DATE.
Składnia:
Składnia |
Przeznaczenie |
Przykład |
AVG( [DISTINCT | ALL] num) |
Zwraca wartość średnią ignorując wartości puste |
SELECT AVG(placa) "Srednia" FROM pracownicy |
COUNT( [DISTINCT | ALL] expr) |
Zwraca liczbę wierszy, w których expr nie jest równe NULL |
SELECT COUNT(nazwisko) "Liczba" FROM pracownicy |
COUNT(*) |
Zwraca liczbę wierszy w tabeli włączając powtarzające się i równe NULL |
SELECT COUNT(*) "Wszystko" FROM pracownicy |
MAX( [DISTINCT | ALL] expr) |
Zwraca maksymalną wartość wyrażenia |
SELECT MAX(Placa) "Max" FROM pracownicy |
MIN( [DISTINCT | ALL] expr) |
Zwraca minimalną wartość wyrażenia |
SELECT MIN(Placa) "Min" FROM pracownicy |
STDDEV( [DISTINCT | ALL] num) |
Zwraca odchylenie standardowe wartości num ignorując wartości NULL. |
SELECT STDDEV(Placa) "Odchylenie" FROM pracownicy |
SUM( [DISTINCT | ALL] num) |
Zwraca sumę wartości num. |
SELECT SUM(Placa) "Koszty osobowe" FROM pracownicy |
VARIANCE( [DISTINCT | ALL] num) |
Zwraca wariancję wartości num ignorując wartości NULL |
SELECT VARIANCE(Placa) "Wariancja" FROM pracownicy |
Funkcje konwersji służą do zamiany wartości jednego typu na wartość innego typu. Ogólnie nazwy funkcji konwersji tworzone są według następującego schematu: typ TO typ. Pierwszy typ jest typem, z którego wykonywana jest konwersja, drugi jest typem wynikowym.
Składnia:
Składnia |
Przeznaczenie |
Przykład |
CHARTOROWID (string) |
Wykonuje konwersję ciągu znaków na ROWID |
SELECT nazwisko FROM pracownicy WHERE ROWID = CHARTOROWID ('0000000F.0003.0002') |
CONVERT(string [,dest_char_set [,source_char_set ] ]) |
Wykonuje konwersję pomiędzy dwoma różnymi implementacjami zestawu znaków. Zestawem domyślnym jest US7ASCII. |
SELECT CONVERT ('New WORD', 'US7ASCII', 'WE8HP') "Conversion" FROM DUAL |
HEXTORAW (string) |
Konwertuje ciąg znaków zawierający cyfry szesnastkowe na wartość binarną, którą można umieścić w polu typu |
RAW INSERT INTO GRAPHICS (RAW_COLUMN) SELECT HEXTORAW ('7D') FROM DUAL |
ROWTOHEX(raw) |
Przekształca wartość typu raw na tekst zawierający cyfry szesnastkowe odpowiadające podanej liczbie. |
SELECT RAWTOHEX (RAW_COLUMN) "Graphics" FROM GRAPHICS |
ROWIDTOCHAR |
Przekształca identyfikator wiersza na tekst. Wynik konwersji ma zawsze długość 18 znaków. |
SELECT ROWID FROM GRAPHICS WHERE ROWIDTOCHAR(ROWID) LIKE '%F38%' |
TO_CHAR(n [, fmt]) |
(konwersja numeryczna) Konwertuje wartość numeryczną na znakową używając opcjonalnego ciągu formatującego. Jeśli ciąg formatujący nie jest podany, to wartość jest konwertowana tak, by zawrzeć wszystkie cyfry znaczące. |
SELECT TO_CHAR(17145, '$099,999') "Char" FROM DUAL |
TO_CHAR(d [, fmt]) |
(konwersja daty) Konwertuje datę na tekst, używając podanego formatu. |
SELECT TO_CHAR(HIREDATE, 'Month DD, YYYY') "New date format" FROM EMP WHERE ENAME = 'SMITH' |
TO_DATE(string [, fmt]) |
Przekształca ciąg znaków w datę. Używa danych aktualnych, jeśli nie mogą być one odczytane z podanego tekstu. Do konwersji używany jest podany ciąg formatujący lub wartość domyślna postaci "DD MON-YY" |
INSERT INTO BONUS (BONUS_DATE) SELECT TO_DATE ('January 15, 1989', 'Month dd, YYYY') FROM DUAL |
TO_NUMBER (string) |
Przekształca tekst zawierający zapis liczby na liczbę |
UPDATE EMP SET SAL = SAL + TO_NUMBER( SUBSTR('$100 raise', 2, 3)) WHERE ENAME = 'BLAKE' |
Składnia:
Składnia |
Przeznaczenie |
Przykład |
ADD_MONTHS (date, n) |
Zwraca padaną datę powiekszoną o podaną liczbę miesięcy n. Liczba ta może być ujemna |
SELECT ADD_MONTHS (HIREDATE, 12) "Next year" FROM EMP WHERE ENAME = 'SMITH' |
LAST_DAY(date) |
Zwraca datę będącą ostatnim dniem w miesiącu zawartym w podanej dacie. |
SELECT LAST_DAY (SYSDATE) "Last" FROM DUAL |
MONTHS_BETWEEN (date1, date2) |
Zwraca liczbę miesięcy pomiędzy datami date1 i date2. Wynik może być dodatni lub ujemny. Część ułamkowa jest częścią miesiąca zawierającego 31 dni. |
SELECT MONTHS_BETWEEN ('02-feb-86', '01-jan-86')) "Months" |
NEW_TIME(date, a, b) |
Zwraca datę i czas w strefie czasowej b, jeśli data i czas w strefie a są równe date. Parametry a i b są wyrażeniami znakowymi i mogą być jednym z: AST, ADT -Atlantic Standard or Daylight Time BST, BDT -Bering Standard or Daylight Time CST, CDT -Central Standard or Daylight Time EST, EDT -Eastern Standard or Daylight Time GMT - Greenwich Mean Time HST, HDT-Alaska-Hawaii Standard or Daylight Time MST, MDT -Mountain Standard or Daylight Time NST - Newfoundland Standard Time PST, PDT -Pacific Standard or Daylight Time YST, YDT -Yukon Standard or Daylight Time |
SELECT TO_CHAR( NEW_TIME(TO_DATE( '17:47', 'hh24:mi'), 'PST', 'GMT'), 'hh24:mi') "GREENWICH TIME" FROM DUAL |
NEXT_DAY(date, string) |
Zwraca datę pierwszego dnia tygodnia podanego w string, który jest późniejszy niż data date. Parametr string musi być poprawną nazwą dnia |
SELECT NEXT_DAY( '17-MAR-89', 'TUESDAY') "NEXT DAY" FROM DUAL |
ROUND(date [, fmt]) |
Zwraca datę zaokrągloną do jednostki zaokrąglania podanej w fmt. Domyślnie jest to najbliższy dzień. |
SELECT ROUND ( TO_DATE( '27-OCT-88'), 'YEAR') "FIRST OF THE YEAR" FROM DUAL |
SYSDATE |
Zwraca aktualny czas i datę. Nie wymaga podania argumentów. |
SELECT SYSDATE FROM DUAL |
TRUNC(date [, fmt]) |
Zwraca datę obciętą do jednostki podanej w fmt. Domyślnie jest to dzień, tzn. usuwana jest informacja o czasie. |
SELECT TRUNC( TO_DATE('28-OCT-88', 'YEAR') "First Of The Year" FROM DUAL |
W funkcjach ROUND i TRUNC można używać następujących tekstów do identyfikacji jednostki zaokrąglenia lub obcięcia:
CC, SCC |
wiek |
SYYY, YYYY, YEAR, SYEAR, YYY, YY, Y |
rok (zaokrąglenie w zwyż od 1.07) |
Q |
kwartał (zaokrąglenie w górę od 16tego drugiego miesiąca) |
MONTH, MON, MM |
miesiąc (zaokrąglenie w górę od 16) |
WW |
pierwszy tydzień roku |
W |
pierwszy tydzień miesiąca |
DDD, DD, J |
dzień |
DAY, DY, D |
najbliższa niedziela |
HH, HH12, HH24 |
godzina |
MI |
minuta |
Składnia:
Składnia |
Przeznaczenie |
Przykład |
GREATEST(expr [, expr] ...) |
Znajduje największą z listy wartości. Wszystkie wyrażenia począwszy od drugiego są konwertowane do typu pierwszego wyrażenia przed wykonaniem porównania. |
SELECT GREATEST ('Harry', 'Harriot', 'Harold') "GREATEST" FROM DUAL |
LEAST(expr [, expr] ...) |
Zwraca najmniejszą z listy wartości. Wszystkie wyrażenia począwszy od drugiego są konwertowane do typu pierwszego wyrażenia przed wykonaniem porównania. |
SELECT LEAST ('Harry', 'Harriot', 'Harold') "LEAST" FROM DUAL |
NVL (expr1, expr2) |
Jeśli expr1 jest równe NULL, to zwraca expr2, w przeciwnym wypadku zwraca expr1. |
SELECT ENAME NVL(TO_CHAR(COMM), 'NOT APPLICABLE') "COMMISION" FROM EMP WHERE DEPTNO = 30 |
UID |
Zwraca unikalny identyfikator użytkownika wywołującego funkcję. |
SELECT USER, UID FROM DUAL |
USER |
Zwraca nazwę użytkownika |
SELECT USER, UID FROM DUAL |
Formaty zapisu danych używane są w dwóch podstawowych celach:
Formaty zapisu używane są w funkcjach TO_CHAR i TO_DATE.
Formaty numeryczne są używane w połączeniu z funkcją TO_CHAR do przekształcenia wartości numerycznej na wartość znakową. Użycie formatu numerycznego powoduje zaokrąglenie do podanej w nim liczby cyfr znaczących. Jeśli wartość numeryczna ma więcej cyfr z lewej strony niż to zostało przewidziane, to wartość ta zastępowana jest gwiazdką '*'. Poniższa tabela przedstawia elementy, które może zawierać specyfikacja formatu numerycznego:
Element |
Przykład |
Opis |
9 |
9999 |
Liczba '9' określa szerokość wyświetlania |
0 |
0999 |
Pokazuje wiodące zera |
$ |
$9999 |
Poprzedza wartość znakiem '$' |
B |
B9999 |
Wyświetla zera jako spacje (nie jako zera) |
MI |
9999MI |
Wyświetla '-' po wartości ujemnej |
PR |
9999PR |
Wyświetla wartość ujemną w nawiasach kątowych '<', '>' |
, (przecinek) |
9,999 |
Wyświetla przecinek na podanej pozycji |
. (kropka) |
99.99 |
Wyświetla kropkę na podanej pozycji |
V |
999V99 |
Mnoży wartość przez 10n, gdzie n jest liczbą dziewiątek po 'V' |
E |
9.999EEEE |
Wyświetla liczbę w notacji wykładniczej (format musi zawierać dokładnie cztery litery E) |
DATE |
DATE |
Dla dat przechowywanych w postaci numerycznej. Wyświetla datę w formacie 'MM/DD/YY' |
Formaty dat są używane w funkcji TO_CHAR w celu wyświetlenia daty. Mogą być również użyte w funkcji TO_DATE w celu wprowadzenia daty w określonym formacie. Format standardowy, to 'DD-MON-YY'.
Elementy formatu dat przedstawia tabela:
Element |
Opis |
SCC lub CC |
Wiek; 'S' poprzedza daty przed naszą erą znakiem '-' |
YYYY lub SYYYY |
Czterocyfrowy rok, 'S' poprzedza daty przed naszą erą znakiem '-' |
YYY, YY lub Y |
Ostatnie 3, 2 lub 1 cyfra roku |
Y,YYY |
Rok z przecinkiem na podanej pozycji |
SYEAR lub YEAR |
Rok przeliterowany. 'S' powoduje poprzedzenie daty przed naszą erą znakiem '-' |
BC lub AD |
Znak BC/AD (przed naszą erą/naszej ery) |
B.C. lub A.D |
Znak BC/AD z kropkami |
Q |
Kwartał roku (1, 2, 3 lub 4) |
MM |
Miesiąc (01-12) |
MONTH |
Nazwa miesiąca wyrównana do 9 znaków za pomocą spacji |
MON |
Trzyliterowy skrót nazwy miesiąca |
WW |
Tydzień roku (1-52) (tydzień zaczyna się w pierwszy dniu roku i trwa 7 dni) |
W |
Tydzień miesiąca (1-5) (tydzień zaczyna się w pierwszym dniu miesiąca i trwa 7 dni) |
DDD |
Dzień roku (1-366) |
DD |
Dzień miesiąca (1-31) |
D |
Dzień tygodnia (1-7) |
DAY |
Nazwa dnia wyrównana do 9 znaków za pomocą spacji |
DY |
Trzyliterowy skrót nazwy dnia |
AM lub PM |
Wskaźnik pory dnia |
A.M. lub P.M. |
Wskaźnik pory dnia z kropkami |
HH lub HH12 |
Godzina (1-12) |
HH24 |
Godzina (1-24) |
MI |
Minuta (0-59) |
SS |
Sekunda (0-59) |
SSSS |
Sekundy po północy (0-86399) |
/ ., |
Znaki przestankowe umieszczane w wyniku |
"..." |
Ciąg znaków umieszczany w wyniku |
Dodatkowo w ciągu znaków określających format można użyć:
Warunki i wyrażenia składają się z operatorów, funkcji oraz danych, na których działają.
Operatory arytmetyczne działają zasadniczo na danych typu numerycznego. Jednak niektóre z tych operatorów mogą być użyte do danych typu DATE. Spis operatorów arytmetycznych podzielonych według priorytetu przedstawia tabela:
Operator |
Opis |
Przykład |
( ) |
Zmienia normalną kolejność wykonywania działań. Wszystkie działania wewnątrz nawiasów są wykonywane przed działaniami poza nawiasami. |
SELECT (X+Y)/(Y+Z) ... |
+, |
Operatory jednoargumentowe zachowania i zmiany znaku. |
|
*, / |
Mnożenie, dzielenie |
SELECT 2*X+1 ... WHERE X > Y/2 |
+, - |
Dodawanie, odejmowanie |
SELECT 2*X+1... WHERE X > Y-Z |
Jedynym operatorem działającym na ciągach znaków jest operator konkatenacji. Rezultatem działania tego operatora jest ciąg znaków będący połączeniem operandów. Należy pamiętać, że ciągi znaków typu CHAR nie mogą być dłuższe niż 255 znaków. Ograniczenie to dotyczy również ciągu znakowego będącego wynikiem działania operatora konkatenacji.
Operator |
Opis |
Przykład |
|| |
Konkatenacja ciągów znaków |
SELECT 'Nazwa: ' || ENAME ... |
Operatory porównania są wykorzystywane w wyrażeniach i warunkach do porównywania dwóch wyrażeń. Wynikiem działania operatorów porównania jest zawsze wartość logiczna (TRUE lub FALSE).
Operator |
Opis |
Przykład |
( ) |
Zmienia normalną kolejność wykonywania działań |
... NOT (A=1 OR B=1) |
= |
Sprawdza, czy dwa wyrażenia są równe |
... WHERE PLACA = 1000 |
!=, ^=, <> |
Sprawdza, czy dwa wyrażenia są różne |
... WHERE PLACA != 1000 |
> |
Większe niż |
... WHERE PLACA > 1000 |
< |
Mniejsze niż |
... WHERE PLACA < 1000 |
>= |
Większe lub równe niż |
... WHERE PLACA >= 1000 |
<= |
Mniejsze lub równe niż |
... WHERE PLACA <= 1000 |
IN |
Równy dowolnemu elementowi. Synonim do " = ANY" |
|
NOT IN |
Różny od każdego z elementów. Wynikiem jest FALSE jeśli dowolny element zbioru jest równy NULL Synonim do "!= ALL" |
... WHERE PLACA NOT IN (SELECT PLACA FROM PRAC WHERE WYDZIAL=30) |
ANY |
Porównuje wartość z każdą wartością ze zbioru po prawej stronie. Musi być poprzedzony jednym z operatorów: =, !=, >, <, <=, >=. Zwraca TRUE, jeśli przynajmniej jeden z elementów spełnia podany warunek. |
WHERE WYDZIAL=30) |
ALL |
Porównuje wartość z każdą wartością ze zbioru po prawej stronie. Musi być poprzedzony jednym z operatorów: =, !=, >, <, <=, >=. Zwraca TRUE, jeśli każdy z elementów spełnia podany warunek. |
...WHERE (PLACA, PREMIA) >= ALL ((14900, 300), (3000, 0)) |
[NOT] BETWEEN x AND y[Nie] |
większy lub równy x i mniejszy lub równy y. |
... WHERE A BETWEEN 1 AND 9 |
[NOT] EXISTS |
Zwraca TRUE jeśli zapytanie [nie] zwraca przynajmniej jeden wiersz. |
... WHERE EXISTS (SELECT PLACA FROM PRAC WHERE WYDZIAL= 30) |
[NOT] LIKE[Nie] |
spełnia podany wzorzec. Litera '%' jest używana do zapisywania dowolnego ciągu znaków (0 lub więcej), który nie jest równy NULL. Litera '_' zastępuje dowolną pojedynczą literę. |
... WHERE STAN LIKE 'T%' |
IS [NOT] NULL [Nie] |
jest równe NULL. |
... WHERE ZAWOD IS NULL |
Operator NOT IN zwróci FALSE (co w przypadku klauzuli WHERE spowoduje, że żadne wiersze nie zostaną zwrócone), jeśli choć jeden z elementów listy jest równy NULL. Np. rozkaz:
SELECT 'TRUE'
FROM prac
WHERE wydzial NOT IN (5, 15, NULL) ;
nie zwróci żadnych wierszy, ponieważ
wydzial NOT IN (5, 15, NULL)
zostanie rozwinięty do
wydzial != 5 AND wydzial != 15 AND wydzial != NULL
Wynikiem działania operatorów porównania i logicznych dla wartości NULL jest wartość NULL. Dlatego też wynikiem całego opisywanego rozkazu będzie wartość NULL.
Operatory logiczne służą do wykonywania obliczeń na wartościach typu logicznego (w szczególności będących wynikiem obliczania warunków).
Operator |
Opis |
Przykład |
( ) |
Zmienia normalną kolejność wykonywania działań |
SELECT ... WHERE x = y AND (a = b OR p = q) |
NOT |
Zaprzeczenie wyrażenia logicznego |
|
AND |
Logiczne 'i'. Wynik jest równy TRUE, jeśli wartości obu operandów są równe TRUE |
... WHERE A = 1 AND B = 2 |
OR |
Logiczne 'lub'. Wynike jest równy TRUE, jeśli wartość przynajmniej jednego operandu jest równa TRUE |
... WHERE A = 1 OR B = 3 |
Poniższe tabele przedstawiają wynik działania operatora AND i OR dla różnych wartości:
AND |
true |
false |
null |
True |
true |
false |
null |
False |
false |
false |
false |
Null |
null |
false |
null |
OR |
true |
false |
null |
True |
true |
true |
true |
False |
true |
false |
null |
Null |
true |
null |
null |
Operatory zbiorowe działają na wynikach zapytań lub listach wartości.
Operator |
Opis |
Przykład |
UNION |
Unia dwóch zbiorów. Łączy dwa zbiory, powtarzające się elementy występują tylko raz. |
... SELECT ... UNION SELECT ... |
INTERSECT |
Część wspólna dwóch zbiorów. Powtarzające się elementy występują tylko raz. |
... SELECT ...INTERSECT SELECT ... |
MINUS |
Oblicza różnicę dwóch zbiorów. W wyniku umieszczane są tylko te elementy, które występują w pierwszym zbiorze i nie występują w drugim. Elementy powtarzające się występują tylko raz. |
... SELECT ...MINUS SELECT ... |
Problemy wynikające przy interpretacji poleceń SQL zilustrujemy przykładami.
Przykład. Mamy dwa pliki FR i FS rekordów odpowiednio typu R(A,B) i S(C,D). Chcemy utworzyć plik rekordów FR×S typu R(A,B)×S(C,D).
|
Pamięć zewnętrzna |
|
|
|
RAM |
|
|
R |
|
|
|
R |
|
FR |
....... |
|
|
|
........ |
|
|
R |
|
bufor |
|
R |
|
|
: |
|
|
|
S |
|
|
S |
|
|
|
|
|
FS |
....... |
|
|
|
Aplikacja |
|
|
S |
|
|
|
|
|
|
: |
|
|
|
OS |
|
|
|
|
|
|
|
|
FR×S |
|
|
|
|
|
|
|
|
|
|
|
|
|
Przypuśćmy, że
Wówczas:
Zatem całkowita liczba dostępów do bloków wynosi
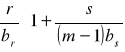
.
Jeżeli r=s=10 000, br= bs =5 i m=100 to liczba dostępów wynosi 42 400 (przy 20 dostępach na sekundę zajmie to 35 minut).
Operację tą można przyspieszyć przyjmując, że plik FR mieści się w mniejszej ilości bloków.
Przykład. Mamy dwa pliki FR i FS rekordów odpowiednio typu R(A,B) i S(C,D).
A |
B |
|
C |
D |
a1 |
1 |
|
2 |
7 |
a2 |
2 |
|
1 |
99 |
a3 |
3 |
|
|
|
Chcemy utworzyć plik rekordów FR×S typu R(A,B)×S(C,D) przy dodatkowym założeniu, że B=C i D=99. Można to otrzymać poleceniem SQL postaci:
Select A,B,C,D From FR , FS Where (B=C) And (D=99);
Polecenie to możemy zinterpretować na dwa sposoby:
Pierwszy sposób:
W pierwszej kolejności wykonujemy operację złączenia w wyniku, której otrzymamy relację:
A |
B |
C |
D |
|
a1 |
1 |
2 |
7 |
|
a1 |
1 |
1 |
99 |
* |
a2 |
2 |
2 |
7 |
|
a2 |
2 |
1 |
99 |
|
a3 |
3 |
2 |
7 |
|
a3 |
3 |
1 |
99 |
|
W drugiej kolejności dokonujemy operację selekcji z warunkami B=C i D=99
Drugi sposób:
W pierwszej kolejności dokonujemy selekcji z warunkiem D=99 w pliku FS
C |
D |
1 |
99 |
W drugiej kolejności dokonujemy operację złączenia otrzymanej relacji z plikiem FR
A |
B |
C |
D |
|
a1 |
1 |
1 |
99 |
* |
a2 |
2 |
1 |
99 |
|
a3 |
3 |
1 |
99 |
|
W trzeciej kolejności dokonujemy selekcji z warunkiem B=C.
Przykład. Mamy dwa pliki FR i FS rekordów odpowiednio typu R(A,B) i S(C,D). Chcemy wykonać polecenie SQL postaci:
Select A,B,C,D From FR , FS Where B=C;
Pliki FR i FS są duże i żaden z nich nie mieści się w pamięci operacyjnej. Pewnymi sposobami optymalizacji takiego zapytania mogą być:
Rozkazy języka SQL są niewystarczające do tworzenia efektywnych systemów baz danych, a w szczególności do kontroli warunków integralności bazy w momencie wprowadzania do niej danych. Dlatego firma Oracle wprowadziła rozszerzenia proceduralne do swojej implementacji języka SQL i tak powstały język nazwała PL/SQL. PL/SQL pozwala wykorzystywać prawie wszystkie operacje standardowego SQL. Wyjątkiem są tu operacje definiowania danych (ALTER, CREATE i RENAME) oraz niektóre rozkazy kontroli danych jak CONNECT, GRANT i REVOKE. Kod napisany w PL/SQL składa się z rozkazów standardowego SQL oraz rozszerzeń proceduralnych. Możliwe jest stosowanie wszystkich standardowych funkcji SQL w rozkazach SQL oraz prawie wszystkich (tj. z wyłączeniem funkcji grupowych) w rozszerzeniach. Każdy rozkaz PL/SQL kończy się średnikiem. PL/SQL pozwala na definiowanie zmiennych. Zmienne służą do przechowywania wyników zapytań i obliczeń w celu ich późniejszego wykorzystania. Jednak wszystkie zmienne muszą być zadeklarowane przed ich użyciem. Każda zmienna posiada typ. Typy zmiennych są takie same jak typy stosowane w SQL'u. Zmienne deklaruje się pisząc nazwę zmiennej a następnie jej typ, np.:
premia NUMBER(7, 2);
Wartość do zmiennej przypisuje się za pomocą operatora przypisania ":=", np.:
podatek := cena * stopa;
Druga możliwość nadania wartości zmiennej to użycie rozkazu SELECT lub FETCH do wpisania wartości do zmiennej:
SELECT placa INTO placa_aktualna FROM pracownicy
WHERE nazwisko = 'Nowak' ;
PL/SQL posiada zmienne strukturowe nazywane rekordami, które podzielone są na pola. Istnieje możliwość deklarowania stałych. Deklaracja taka jest podobna do deklaracji zmiennej, ale konieczne jest dodatkowo użycie słowa CONSTANT i natychmiastowe przypisanie wartości do zmiennej. Deklarację stałej pokazuje następujący przykład:
stopa_premii CONSTANT NUMBER(3, 2) := 0.10;
Wszystkie obiekty posiadają atrybuty. Jednym z nich jest typ (zarówno zmiennej jak i kolumny). Możliwe jest użycie zapisu %TYPE w celu zapisania typu np. w deklaracji zmiennej. Zapis taki pozwala zadeklarować zmienną o takim samym typie jak inna zmienna lub kolumna (należy przy tym zauważyć, że typ ten nie jest znany osobie piszącej program):
tytul books.tytul%TYPE
Możliwe jest również zadeklarowanie rekordu odpowiadającego jednemu wierszowi tabeli. W tym celu należy użyć konstrukcji %ROWTYPE. W PL/SQL można stosować następujące operatory porównań: =, !=, <, >, >=, <=. Mogą one działać na operandach różnych typów: numerycznym, daty i ciągach znaków (wykonują wtedy porównanie leksykalne).
Kod języka PL/SQL jest podzielony na bloki. Blok ma następującą strukturę:
DECLARE
deklaracje
BEGIN
rozkazy wykonywalne
EXCEPTION
obsługa sytuacji wyjątkowych
END;
Każdy blok może zawierać inne bloki, tzn. bloki mogą być zagnieżdżone. W PL/SQL identyfikator jest nazwą dowolnego obiektu (tj. stałej, zmiennej, rekordu, kursora lub wyjątku). Nie jest możliwa dwukrotna deklaracja tego samego identyfikatora w jednym bloku. Można jednak zadeklarować te same identyfikatory w dwóch różnych blokach. Oba takie obiekty są różne i jakakolwiek zmiana w jednym z nich nie powoduje zmiany w drugim. Zakres obowiązywania identyfikatora określa, w którym bloku mogą wystąpić do niego odwołania. Blok ma dostęp tylko do obiektów lokalnych i globalnych. Identyfikatory zadeklarowane w bloku są lokalne dla tego bloku i globalne dla wszystkich bloków w nim zawartych (podbloków). Identyfikatory globalne mogą zostać zredefiniowane w podblokach, co powoduje, że obiekt lokalny ma pierwszeństwo przed globalnym. Dostęp do obiektu globalnego jest możliwy w tym przypadku tylko wtedy, gdy użyta zostanie nazwa odpowiedniego bloku. Blok nie ma dostępu do obiektów zadeklarowanych w innych blokach na tym samym poziomie zagnieżdżenia, ponieważ nie są one ani lokalne, ani globalne w tym bloku.
PL/SQL w wersji 2.0 pozwala na definiowanie funkcji i procedur.
Składnia definicji procedury jest następująca:
PROCEDURE name [ (parameter [, parameter] ... ) ] IS
[local declarations]
BEGIN
executable statements
[EXCEPTION
exception handlers]
END [name];
Składnia definicji parametrów jest następująca:
var_name [IN | OUT | IN OUT] datatype
[{ := | DEFAULT } value]
Określenie typu dla danego parametru nie może zawierać ograniczeń, tzn. nie jest możliwe zapisanie np. INT(5).
Procedura składa się z dwóch części - nagłówka i ciała. Nagłówek rozpoczyna się słowem PROCEDURE i kończy na nazwie procedury lub liście parametrów. Deklaracja parametrów jest opcjonalna. Procedury bezparametrowe zapisuje się bez nawiasów. Ciało procedury rozpoczyna się słowem IS a kończy słowem END (po którym może opcjonalnie wystąpić nazwa procedury). Część deklaracyjna (pomiędzy słowem IS i BEGIN) zawiera deklaracje obiektów lokalnych. W tym przypadku nie używa się słowa DECLARE. Część wykonywalna (pomiędzy BEGIN a EXCEPTION lub END) zawiera rozkazy języka PL/SQL. W tej części musi wystąpić conajmniej jeden rozkaz.
Definicję procedury zwiększającą płacę wybranego pracownika pokazuje przykład:
PROCEDURE zwieksz (prac_id INTEGER, kwota REAL) IS placa_aktualna REAL;
BEGIN
UPDATE pracownicy SET placa_podstawowa = placa_podstawowa + kwota
WHERE prac_id = id_pracownika;
END zwieksz;
Zadaniem funkcji jest obliczenie wartości. Definicja funkcji jest taka sama jak procedury z tym wyjątkiem, że funkcja posiada klauzulę RETURN.
FUNCTION name [ (argument [, argument] ... ) ]
RETURN datatype IS [local declarations]
BEGIN
executable statements
[EXCEPTION
exception handlers]
END [name];
Wewnątrz funkcji musi pojawić się przynajmniej jeden rozkaz RETURN. Rozkaz RETURN natychmiast kończy wykonanie funkcji i zwraca sterowanie do modułu wywołującego. W przypadku funkcji musi wystąpić przynajmniej jeden rozkaz RETURN, w którym musi być wyrażenie. Wynik tego wyrażenia musi mieć taki typ jak podany w nagłówku. Jeśli funkcja nie kończy się rozkazem RETURN, to PL/SQL zgłosi odpowiedni wyjątek. W przypadku procedury rozkaz RETURN nie może zawierać żadnego wyrażenia.
W celu wykonania rozkazu SQL system tworzy pewien obszar roboczy nazywany przestrzenią kontekstu. W przestrzeni tej przechowywane są informacje konieczne do wykonania rozkazu. PL/SQL pozwala nazwać przestrzeń kontekstu i odwoływać się do zawartych w niej danych za pomocą mechanizmu nazywanego kursorem. PL/SQL używa dwóch typów kursorów:
Jeśli zapytanie zwraca wiele wierszy, to możliwe jest utworzenie kursora, który będzie umożliwiał dostęp do pojedynczych wierszy ze zwracanej listy. Kursor definiuje się w części deklaracji bloku PL/SQL przez nazwanie go i specyfikację zapytania. Sposób deklaracji kursora pokazuje przykład:
DECLARE
CURSOR prac_kursor IS SELECT nazwisko, wydział
FROM pracownicy
WHERE płaca > 2000 ;
...
BEGIN
.....
END;
Sama deklaracja nie powoduje wykonania występującego w niej zapytania. Do tego konieczne jest otwarcie kursora, którego można dokonać instrukcją OPEN w następujący sposób:
OPEN prac_kursor;
W celu odczytania pojedynczego wiersza z kursora konieczne jest następnie użycie rozkazu FETCH. Każdy kolejny rozkaz FETCH dla danego kursora powoduje odczytanie kolejnego wiersza. Rozkaz FETCH może być użyty w następujący sposób:
FETCH prac_kursor INTO prac_nazw, prac_wydz;
Po zakończeniu pracy z kursorem konieczne jest poinformowanie o tym systemu w celu zwolnienia zasobów. Dokonuje się tego rozkazem CLOSE, np.:
CLOSE prac_kursor;
Każdy kursor posiada pewne atrybuty, których wartości informują o jego stanie. Nazwy atrybutów poprzedzone są znakiem '%' i wpisywane bezpośrednio po nazwie kursora. Zdefiniowano następujące atrybuty kursorów:
Następujące przykłady pokazują sposób użycia atrybutów kursora:
LOOP
FETCH prac_kursor INTO prac_nazw, prac_wydz;
IF prac_kursor%ROWCOUNT > 10 THEN
wiecej niż 10
...
EXIT WHEN prac_kursor%NOTFOUND;
...
END LOOP;
W języku PL/SQL rekordem nazywana jest zmienna złożona, będąca grupą zmiennych elementarnych. Każda zmienna elementarna w rekordzie nazywana jest polem. Rekordy są używane najczęściej do przechowywania zawartości pojedynczego wiersza w bazie danych. PL/SQL pozwala definiować rekordy odpowiadające pojedynczym wierszom w tabeli, widoku lub kursorze, nie pozwala jednak na definiowanie typów poszczególnych pól. Deklarowanie rekordu najlepiej jest wyjaśnić na przykładzie. Jeśli wystąpiła deklaracja kursora w tabeli pracownicy, który zwraca nazwisko, wydział i datę zatrudnienia, to możliwe jest zadeklarowanie odpowiedniego rekordu za pomocą atrybutu %ROWTYPE:
DECLARE
CURSOR prac_kursor IS
SELECT nazwisko, wydzial, data_zatrudnienia
FROM pracownicy;
prac_rek prac_kursor%ROWTYPE
...
FETCH prac_kursor INTO prac_rek;
Rekord może być tworzony nie tylko za pomocą kursora, ale również za pomocą nazwy tabeli w następujący sposób:
nazwa_rekordu nazwa_tabeli%ROWTYPE;
Rzeczywistą deklarację pokazuje przykład:
DECLARE prac_rek pracownicy%ROWTYPE; ... BEGIN ... END;
Dostęp do pola rekordu możliwy jest za pomocą nazwy tego rekordu i poprzedzonej kropką nazwy pola: nazwa_rekordu.nazwa_pola; Aby więc dodać pojedyncze wynagrodzenie do sumy (przy użycia zdefiniowanego wcześniej rekordu prac_rek) można napisać:
suma := suma + prac_rek.placa;
Możliwe jest przypisanie wartości do pola rekordu lub rekordu jako całości. Należy jednak pamiętać, że rekord jest zmienną i zmiana wartości jego pól nie powoduje zmiany wartości odpowiedniego wiersza w bazie danych. Przypisania wartości do pola rekordu można dokonać za pomocą operatora przypisania ':=' w następujący sposób:
nazwa_rekordu.nazwa_pola := plsql_wyrażenie;
Użycie tej konstrukcji ilustruje przykład:
prac_rek.nazwisko := UPPER(prac_rek.nazwisko);
Przypisanie zawartości całego możliwe jest na dwa sposoby:
Użycie tych dwóch operacji ilustruje przykład:
DECLARE
prac_rek1 pracownicy%ROWTYPE;
prac_rek2 pracownicy%ROWTYPE;
BEGIN
SELECT nazwisko, imie, wydzial, placa_podstawowa
INTO prac_rek1 FROM pracownicy
WHERE wydzial = 30;
prac_rek2 := prac_rek1;
...
END;
PL/SQL niejawnie deklaruje rekord w pętli FOR dla kursora. Sytuację tę ilustruje przykład:
DECLARE
CURSOR prac_kursor IS
SELECT nazwisko, imie, wydzial, placa_podstawowa
FROM pracownicy;
BEGIN
FOR pracownik IN prac_kursor LOOP
suma := suma + pracownik.placa_podstawowa;
...
END LOOP;
Niejawnie deklarowanym rekordem jest tu zmienna o nazwie pracownik. Zmienna ta jest automatycznie deklarowana tak, jakby wystąpiła jawna deklaracja postaci nazwa_kursora%ROWTYPE.
Błędy podczas wykonania programu powodowane są wieloma różnymi przyczynami. Wśród nich można wymienić następujące: błędy projektowe, błędy kodowania, uszkodzenia sprzętu, niewłaściwe dane itp. Nie jest możliwe przewidzenie wszystkich możliwych błędów, można jednak zaplanować obsługę niektórych z nich. W starszych językach programowania błąd taki jak "Przepełnienie stosu" powodował zgłoszenie komunikatu i zakończenie wykonania programu. W nowoczesnych językach (C++, Java, PL/SQL) zmieniło się podejście do obsługi błędów. Języki te udostępniają bowiem mechanizm nazywany obsługą wyjątków, który pozwala zdefiniować akcję wywoływaną w momencie wystąpienia błędu i dalej kontynuować wykonanie programu. Wyjątkiem nazywamy spełnienie warunków wystąpienia błędów. Wyjątki dzielą się na predefiniowane (przez twórców języka) i definiowane przez użytkownika. Przykładami wyjątków predefiniowanych mogą być: "Out of memory", "Division by zero". W języku PL/SQL użytkownik może definiować wyjątki w części deklaracyjnej bloku PL/SQL. Przykładowo możliwe jest zdefiniowanie wyjątku "Płaca poniżej minimalnej", aby wskazać, że proponowana płaca jest zbyt niska. Gdy zachodzi błąd, to wyjątek jest wywoływany (raise), tzn. wykonywanie programu zostaje przerwane i sterowanie jest przekazywane do odpowiedniego fragmentu programu, którego zadaniem jest obsługa danego wyjątku (funkcji obsługi wyjątku). Wyjątki predefiniowane są wykrywane i wywoływane automatycznie. Wyjątki użytkownika muszą być wywołane jawnie za pomocą rozkazu RAISE. W momencie zaistnienia wyjątku wykonanie aktualnego bloku kończy się, następnie wywołuje się funkcję obsługi tego wyjątku i sterowanie jest zwracane do następnej instrukcji w bloku zawierającym blok, w którym wystąpił wyjątek. Jeśli taki blok nie istnieje to sterowanie jest zwracane do systemu. Przykładowy fragment programu zawierający wyjątek "dzielenie przez zero" (ZERO_DIVIDE) oraz jego obsługę obliczający wskaźnik giełdowy C/Z:
DECLARE
cz_wsk NUMBER(3,1);
BEGIN
...
SELECT cena / zysk FROM akcje
WHERE nazwa = 'ABC'; -- może wywołać wyjątek - ZERO_DIVIDE
INSERT INTO informacje (nazwa, c_z)
VALUES ('ABC', cz_wsk);
COMMIT
EXCEPTION
WHEN ZERO_DIVIDE THEN
INSERT INTO informacje (nazwa, c_z)
VALUES ('ABC', NULL);
COMMIT;
...
WHEN OTHERS THEN
ROLLBACK;
END;
Posługiwanie się wyjątkami ma wiele zalet. Za pomocą uprzednio stosowanych technik kontrola wystąpienia błędów byłą bardzo złożona i prowadziła do znacznego skomplikowania kodu programu. W szczególności konieczne mogło być sprawdzanie poprawności wykonania każdego rozkazu:
BEGIN
SELECT ...
-- kontrola błędu "brak danych"
SELECT ...
-- kontrola błędu "brak danych"
SELECT ...
-- kontrola błędu "brak danych"
END;
Ponadto kod obsługi błędu nie był odseparowany od kodu wykonywanego normalnie, co zmniejszało przejrzystość programu i powodowało, że algorytmy stawały się nieczytelne.
Ten sam problem można znacznie prościej i łatwiej rozwiązać za pomocą wyjątków:
BEGIN
SELECT ...
SELECT ...
SELECT ...
EXCEPTION
WHEN NO_DATA_FOUND THEN
... -- obsługa wszystkich błędów "brak danych"
END;
Wyjątki nie tylko zwiększają czytelność programu i upraszczają jego konstrukcję. Zapewniają również, że wszystkie błędy zostaną obsłużone. Jeśli odpowiedniej funkcji nie ma w aktualnym bloku, to wyjątek jest przekazywany do bloku nadrzędnego, aż do znalezienia funkcji obsługi lub powrotu do systemu.
Twórcy języka PL/SQL zdefiniowali zestaw wyjątków, związanych z systemem zarządzania bazą danych i językiem. Wyjątki te wywoływane są automatycznie w momencie zajścia odpowiednich warunków. Wybrane z nich przedstawione są poniżej:
Aby obsłużyć ("złapać") wyjątek konieczne jest napisane własnej funkcji obsługi tego wyjątku. Dokonuje się tego w części bloku PL/SQL rozpoczynającej się słowem kluczowym EXCEPTION, które występuje zawsze na końcu bloku. Każda funkcja obsługi wyjątku składa się ze słowa WHEN, po którym podaje się nazwę wyjątku oraz słowa THEN, po którym występuje ciąg instrukcji wykonywanych w momencie zajścia podanego błędu. Funkcja obsługi wyjątku kończy wykonanie bloku, w związku z czym nie jest możliwy powrót do miejsca, w którym błąd wystąpił. Opcjonalne słowo OTHERS (zamiast nazwy wyjątku) pozwala zdefiniować funkcję obsługi wszystkich pozostałych wyjątków (tzn. nie wymienionych wcześniej). Ostatecznie część EXCEPTION wygląda następująco:
EXCEPTION
WHEN ... THEN
-- obsługa wyjątku
WHEN ... THEN
-- obsługa wyjątku
WHEN ... THEN
-- obsługa wyjątku
WHEN OTHERS THEN
-- obsługa pozostałych wyjątków
END;
Jeśli zachodzi potrzeba przypisania tej samej akcji różnym wyjątkom, to można nazwy tych wyjątków wypisać w klauzuli WHEN oddzielając słowem OR: WHEN over_limit OR under_limit OR VALUE_ERROR THEN
Nie można jednak użyć słowa OTHERS w takiej liście. Słowo OTHERS zawsze musi wystąpić oddzielnie. Należy pamiętać również, że dla jednego wyjątku może być zdefiniowana tylko jedna funkcja obsługi w danym bloku. W funkcjach obsługi wyjątków mają zastosowanie normalne reguły przesłaniania tzn. widoczne są tylko zmienne globalne lub lokalne.
Język PL/SQL pozwala użytkownikowi na definiowanie swoich własnych wyjątków.Wyjątki takie muszą być jawnie zadeklarowane i w przypadku zajścia odpowiednich warunków, jawnie wywołane za pomocą rozkazu RAISE. Wyjątki deklaruje się podobnie jak zmienne, z tą różnicą, że zamiast nazwy typu występuje słowo EXCEPTION. Deklarowanie wyjątku ilustruje następujący przykład:
DECLARE overflow EXCEPTION; result NUMBER(5); BEGIN ... END;
Należy zwrócić uwagę, że wyjątek w języku PL/SQL nie jest obiektem (w przeciwieństwie do zmiennych), ale informacją o spełnieniu pewnych określonych warunków. W związku z tym do wyjątku nie jest możliwe przypisanie żadnej wartości, ani skojarzenie z nim dodatkowej informacji. Wyjątek nie może być również używany w rozkazach SQL. Nie jest możliwa deklaracja tego samego wyjątku dwa razy w tym samym bloku. Można jednak zadeklarować ten sam wyjątek w różnych blokach. Jak podano wcześniej wyjątki predefiniowane wywoływane są przez system automatycznie. Wyjątki zdefiniowane przez użytkownika, muszą być przez niego wywołane. Służy do tego rozkaz RAISE. Użycie tego rozkazu ilustruje przykład:
DECLARE
brak_czesci EXCEPTION;
liczba_czesci NUMBER(4);
BEGIN
...
IF liczba_czesci < 1 THEN
RAISE brak_czesci;
END IF;
...
EXCEPTION
WHEN brak_czesci THEN
-- obsługa błędu "brak części"
END;
Możliwe jest również jawne (za pomocą rozkazu RAISE) wywoływanie predefiniowanych wyjątków:
RAISE INVALID_NUMBER;
Czasami istnieje konieczno¶ć powtórnego wywołania wyjątku z funkcji, która go obsługuje, w celu przekazania go do bloku nadrzędnego. Przykładem może tu być wycofanie transakcji w bloku zagnieżdżonym i zgłoszenie informacji o błędzie w bloku nadrzędnym. W związku z tym możliwe jest użycie rozkazu RAISE w funkcji obsługi wyjątku. Należy pamiętać, że wyjątki zgłoszone w funkcji obsługi innego wyjątku są zawsze przekazywane do bloku nadrzędnego i tam wyszukiwana jest odpowiednia funkcja obsługi zgodnie z zasadami opisanymi wcześniej. Podobnie wyjątki zgłaszane w części deklaracyjnej przekazywane są do bloku nadrzędnego i tam podlegają przetwarzaniu.
Rozkaz OPEN wykonuje zapytanie skojarzone z jawnie zadeklarowanym kursorem i alokuje niezbędne zasoby potrzebne do wykonywania dalszych operacji. Kursor ustawiany tuż przed pierwszym wierszem wyniku zapytania.
Składnia:
OPEN cursor_name
[(input_parameter [, input_parameter] ... )] ;
Parametry:
Parametry w rozkazie OPEN mogą być użyte tylko wtedy, gdy odpowiednia ilość parametrów została podana w deklaracji kursora. Ilość parametrów w instrukcji OPEN musi być równa ilości parametrów w deklaracji kursora. Parametry instrukcji OPEN służą tylko i wyłącznie do wczytywania danych do kursora i nie mogą być stosowane w celu pobrania ich z kursora. Przyporządkowanie parametrów aktualnych (w instrukcji OPEN) do parametrów formalnych (w deklaracji kursora) może odbywać się na dwa sposoby:
przyporządkowanie przez pozycję
przyporządkowanie przez nazwę
W pierwszym przypadku wartość wyrażenia na odpowiedniej pozycji w instrukcji OPEN jest przyporządkowywana parametrowi znajdującemu się na tej samej pozycji w deklaracji kursora. W drugim przypadku parametry mogą być podane w dowolnej kolejności, ale każde wyrażenie musi być poprzedzone nazwą parametru formalnego i znakami '=>'. Sposób użycia obu możliwości ilustrują przykłady:
DECLARE
CURSOR prac_kur(nazw CHAR, wydz NUMBER) IS ...
BEGIN
OPEN prac_kur('Kowalski', 10);
...
OPEN prac_kur(wydz => 15, nazw => 'Nowak');
END;
Można używać równocześnie przyporządkowania przez pozycję i przez nazwę, należy wtedy jednak pamiętać, że parametry przyporządkowywanej przez pozycję muszą wystąpić przed parametrami przyporządkowywanymi przez nazwę.
Rozkaz CLOSE służy do zamknięcia aktualnie otwartego kursora. Każdy kursor przed ponownym otwarciem musi zostać zamknięty. Rozkaz CLOSE zwalnia wszystkie zasoby przydzielone do obsługi kursora.
Składnia:
CLOSE cursor_name ;
Parametry:
cursor_name - nazwa aktualnie otwartego kursora.
Rozkaz FETCH zwraca następny wiersz danych z aktywnego zbioru (danych spełniających warunek rozkazu SELECT w kursorze). Odczytane informacje przechowywane są w zmiennych. Zwrócone dane odpowiadają zawartości kolejnych kolumn w aktualnym wierszu.
Składnia:
FETCH cursor_name INTO
{ record_name |
variable_name [, variable_name] ... } ;
Parametry:
Przykład.
OPEN prac_kursor;
...
LOOP
FETCH prac_kursor INTO prac_rek;
EXIT WHEN prac_kursor%NOTFOUND;
...
END LOOP;
Rozkaz SELECT ... INTO odczytuje informacje z bazy danych i zapisuje je do zmiennych. W języku PL/SQL standardowy (z SQL) rozkaz SELECT został rozszerzony o klauzulę INTO. Aby rozkaz ten działał poprawnie konieczne jest by SELECT zwracał tylko jeden wiersz (w przypadku wielu wierszy należy zadeklarować kursor i za jego pomocą odczytywać dane).
Składnia rozkazu SELECT z klauzulą INTO:
SELECT select_list_item [, select_list_item] ... INTO
{ record_name |
variable_name [, variable_name] ... }
rest_of_select_statement ;
Parametry: zobacz opis rozkazu FETCH.
Przykład.
SELECT nazwisko, placa*12 INTO pnazw, plac_sum
FROM pracownicy
WHERE pracownik_nr = 12345;
Rozkaz IF pozwala na warunkowe wykonywanie rozkazów.
Składnia:
IF plsql_condition THEN seq_of_statements
[ELSEIF plsql_condition THEN seq_of_statements]
...
[ELSE seq_of_statements]
END IF;
Parametry:
Opis:
Rozkaz IF pozwala uzależnić wykonanie rozkazów od wyników obliczania warunku (lub warunków). Jeśli pierwszy z warunków jest prawdziwy, to wykonywany jest ciąg instrukcji po THEN, aż do napotkania odpowiedniego ELSEIF, ELSE lub END IF, a następnie sterowanie przekazywane jest do najbliższego rozkazu po odpowiednim END IF. W przypadku, gdy warunek nie jest spełniony, to sprawdzany jest warunek w pierwszym ELSEIF. Jeśli ten warunek jest spełniony, to wykonywany jest ciąg instrukcji po odpowiadającym mu THEN i wykonanie instrukcji IF się kończy. Jeśli jednak ten warunek również nie jest spełniony, to sprawdzany jest warunek w następnym ELSEIF. Jeśli żaden z warunków nie jest prawdziwy, to wykonywany jest ciąg instrukcji po ELSE (jeśli istnieje). Wynik obliczania warunku równy NULL jest traktowany jako niespełnienie tego warunku.
Przykład.
IF liczba_czesci < 20 THEN ilosc_zamawianych := 50;
ELSEIF liczba_czesci < 30 THEN ilosc_zamawianych := 20;
ELSE ilosc_zamawianych := 5;
END IF;
INSERT INTO zamowienia
VALUES(typ_czesci, ilosc_zamawianych);
Rozkaz LOOP umożliwia tworzenie pętli w języku PL./SQL. Dopuszczalne są cztery rodzaje pętli:
pętle podstawowe
pętle WHILE
pętle FOR numeryczne
pętle FOR dla kursorów
Składnia:
[<<label_name>>]
[ { WHILE plsql_condition } |
{ FOR {numeric_loop_param | cursor_loop_param } } ]
LOOP seq_of_statements END LOOP [ label_name ] ;
Składnia numeric_loop_papram:
index IN [REVERSE] integer_expr .. integer_expr
Składnia cursor_loop_param:
record_name IN
{ cursor_name [(parameter [, parameter] ...)] |
( select_statement ) }
Parametry:
Opis:
Instrukcje w pętli podstawowej są powtarzane bez sprawdzania żadnych warunków. Twórca programu jest odpowiedzialny za zakończenie pętli instrukcją EXIT.
Przykład pętli podstawowej:
<<loop1>> LOOP ... IF (x > 10) THEN EXIT loop1; ... END LOOP loop1;
Pętla WHILE pozwala powtarzać ciąg instrukcji, dotąd dopóki podany warunek jest prawdziwy. Warunek jest obliczany przed każdym powtórzeniem ciągu instrukcji w pętli. W związku z tym ciąg instrukcji może nie wykonać się ani raz.
Przykład.
WHILE x < 10 LOOP ... x := x - y; ... END LOOP;
Pętla FOR pozwala powtarzać podany ciąg instrukcji określoną ilość razy. Do stwierdzenia, które powtórzenie jest aktualnie wykonywane służy zmienna sterująca nazywana indeksem. Indeks może być zwiększany lub zmniejszany.
Przykład.
FOR i IN 1 .. n LOOP
silnia := silnia * n;
END LOOP;
Pętlę FOR można stosować również w celu odczytywania kolejnych wierszy z kursora (lub zapytania). Ciąg instrukcji w pętli wykonywany jest wtedy, dla każdego wiersza.
Przykład.
DECLARE CURSOR prac_kursor IS select * FROM pracownicy; prac_rek prac_kursor%ROWTYPE;
BEGIN
...
FOR prac_rek IN prac_kursor LOOP
suma := suma + prac_rek.placa_podstawowa;
END LOOP;
...
END;
Rozkaz EXIT służy do wyjścia z pętli. Rozkaz ten ma dwie formy: bezwarunkową i warunkową.
Składnia:
EXIT [label_name] [WHEN plsql_condition] ;
Parametry:
*7.14. Rozkaz GOTO
Rozkaz GOTO służy do natychmiastowego przekazania sterowania od rozkazu aktualnego do pierwszego rozkazu występującego po podanej etykiecie.
Składnia deklaracji etykiety:
<< label_name >>
Składnia rozkazu GOTO:
GOTO label_name ;
Opis:
Rozkaz GOTO umożliwia przeniesienie sterowania do innego miejsca w tym samym bloku lub bloku nadrzędnym, ale nie do funkcji obsługi wyjątku. Z funkcji obsługi wyjątku możliwy jest skok do bloku nadrzędnego, ale nie do bloku aktualnego. Nie jest możliwe również przeniesienie sterowania do pętli z zewnątrz. Jeśli rozkaz GOTO używany jest w celu opuszczenia pętli FOR dla kursora, to kursor zamykany jest automatycznie.
Można wyróżnić rozmaite klasy transakcji, od najprostszych - zwykłych operacji aktualizacji bazy - po skomplikowane procedury na wielu wzajemnie powiązanych obiektach. Istnieje zbiór cech, które powinna posiadać każda transakcja. Są to:
Własności te powinny być sprawdzone i zapewnione przez mechanizmy ochrony bazy danych. Nie wszystkie z nich wymagają spełnienia wszystkich wymienionych warunków. Jednak w razie braku możliwości zapewnienia któregokolwiek z wymaganych, transakcja nie może być dopuszczona do realizacji. Gdy brak którejś z własności ujawnił się już w trakcie wykonania transakcji, proces wykonania musi zostać przerwany, a wszelkie wprowadzone zmiany cofnięte.
Można powiedzieć, że transakcja przeprowadza bazę danych z jednego poprawnego i spójnego stanu w drugi. Stany pośrednie wewnątrz transakcji mogą nie spełniać warunków poprawności i spójności. Aby zagwarantować poprawny efekt końcowy, transakcja musi być wykonana w całości albo wcale. Czyli powstanie błędu na jakimś etapie funkcjonowania transakcji musi się wiązać z przywróceniem początkowego stanu bazy danych. W tej sytuacji należy wykorzystać mechanizmy odzyskiwania danych w przypadku błędów pracy systemu.
Istnieje wiele przyczyn powodujących załamanie się procesu wykonania transakcji. Niektóre z nich, to:
Podstawowym problemem jeśli chodzi o zarządzanie transakcjami jest zapewnienie ich czasowej synchronizacji. Trzeba pamiętać, że efekt działania kilku transakcji musi być taki sam jakby były one przeprowadzane po kolei w pewnym ustalonym porządku. Jeśli jest możliwa taka sekwencja operacji, to mówimy, że sekwencja działań jest szeregowalna. Poniższy przykład pokaże jak istotne jest synchronizowanie zachodzących równolegle transakcji.
W systemie rezerwacji miejsc w samolotach, aby zarezerwować bilet na połączenie łączone Warszawa-Londyn-Los Angeles-Honolulu trzeba wykonać następujące kroki:
Nie ma problemu gdy na bazie danych o odlotach samolotów działa w danej chwili tylko jedna transakcja. Sytuacja się komplikuje, gdy w tym samym czasie inne biura podróży chcą zarezerwować miejsca na interesujące nas loty. Wtedy możliwa jest następująca sytuacja: nastąpiło sprawdzenie , że są wolne miejsca ale przed operacją zarezerwowania inna transakcja wcześniej dokonała tej samej operacji i na któryś z kolejnych interesujących nas lotów nie ma już wolnych miejsc. Innego rodzaju błędem jest tylko częściowe wykonanie transakcji, np. z powodu jakiegoś chwilowego błędu w działaniu systemu zarezerwowano tylko dwa z trzech lotów składających się na pełne połączenie. W przypadku takiego błędu konieczne jest przywrócenie bazy do stanu pierwotnego.
Ogólnie mówiąc problemy, które mogą wyniknąć przy jednoczesnym działaniu wielu transakcji równocześnie, można podzielić na dwie kategorie:
w wyniku wykonania takiej sekwencji operacji, otrzymujemy niepoprawną końcową wartość X, tracona jest informacja zapisana przez transakcję T1
wartość X odczytana przez transakcję T3 obliczającą sumę A+...+X+Y nie jest poprawna, gdyż w „międzyczasie” obliczeń, transakcja T1 zdążyła ją zaktualizować
Widać więc jak istotne jest wprowadzenie mechanizmów synchronizujących dostęp do bazy danych i rozstrzygających ewentualne konflikty.
Ponieważ zawsze jest możliwe, aby transakcje były wykonywane po kolei (sekwencyjnie), jest sensownie zakładać, że normalny lub zamierzony wynik jest taki sam jak wynik otrzymany wtedy, kiedy nie jest wykonywana współbieżnie żadna inna transakcja. Załóżmy więc, że współbieżne wykonanie kilku transakcji jest poprawne wtedy i tylko wtedy, gdy jego wynik jest taki sam jak wynik otrzymany przy sekwencyjnym wykonaniu tych samych transakcji w pewnej kolejności.
Dla potrzeb teorii szeregowalności, wprowadźmy potrzebne definicje.
Definicja. Harmonogram zbioru transakcji, jest to kolejność, w której są wykonywane elementarne operacje transakcji (blokowanie, odczyt, zapis, itd.).
Definicja. Harmonogram nazywamy sekwencyjnym (serial) jeśli wszystkie operacje każdej transakcji występują kolejno po sobie.
Definicja. Harmonogram nazywamy szeregowalnym (serializable), jeśli jego wynik jest równoważny wynikowi otrzymanemu za pomocą pewnego harmonogramu sekwencyjnego.
Poniższy przykład uwidacznia różnice pomiędzy harmonogramem sekwencyjnym, szeregowalnym i nieszeregowalnym.
Przykład. Rozważmy dwie transakcje przeksięgowania kwot pieniężnych z konta na konto
T1: READ A; A=A-10; WRITE A; READ B; B=B+10; WRITE B;
T2: READ B; B=B-20; WRITE B; READ C; C=C+20; WRITE C;
Każdy harmonogram sekwencyjny powyższych transakcji ma własność zachowania sumy A+B+C. Przestawienia kolejności wykonywania pojedynczych operacji wewnątrz transakcji, mogą doprowadzić do stworzenia harmonogramów niesekwencyjnych ale szeregowalnych (sytuacja pożądana) albo nieszeregowalnych, (sytuacja niepożądaną).
Poniższe przykłady, to:
T1 |
T2 |
|
T1 |
T2 |
|
T1 |
T2 |
READ A |
|
|
READ A |
|
|
READ A |
|
|
READ B |
|
A+A-10 |
|
|
A=A-10 |
|
A=A-10 |
|
|
|
RAED B |
|
WRITE A |
|
|
B=B-20 |
|
WRITE A |
|
|
READ B |
|
WRITE A |
|
|
|
B=B-20 |
|
B=B+10 |
|
|
WRITE B |
|
RAED B |
|
|
WRITE B |
|
READ B |
|
|
|
WRITE B |
|
|
READ B |
|
READ C |
|
B=B+10 |
|
|
|
B=B-20 |
B=B+10 |
|
|
|
READ C |
|
|
WRITE B |
|
C=C+20 |
|
WRITE B |
|
|
|
READ C |
WRITE B |
|
|
|
C=C+20 |
|
|
C=C+20 |
|
WRITE C |
|
|
WRITE C |
|
|
WRITE C |
(a) (b) (c)
Istnieją dwie metody zapewnienia szeregowalności w współbieżnych procesach realizacji transakcji w bazach danych.
Pierwsza, to zastosowanie programów szeregujących, będących częścią systemu zarządzania bazą danych, odpowiedzialną za rozstrzyganie konfliktów pomiędzy sprzecznymi żądaniami. Pogramy te mogą eliminować sytuacje zakleszczenia i nieszeregowalność poprzez przerwanie wykonania i restart w późniejszym terminie jednej bądź większej ilości transakcji. Dotychczasowe efekty działania przerwanych transakcji są wówczas wymazywane z bazy danych.
Drugą metodą jest zastosowanie protokołów, czyli zbiorów zasad jakie muszą być stosowane przez wszystkie transakcje. Zależnie od protokołu, zasady te mają różne cele: zapewnić szeregowalnośc transakcji, wyeliminować możliwość powstania zakleszczenia, itp. Odpowiednie narzędzia (menadżery transakcji) bazy danych muszą zapewnić przestrzeganie protokołu i w przypadku naruszenia określających go zasad przez którąkolwiek z transakcji, przerwać jej wykonanie oraz przywrócić stan bazy sprzed jej startu.
Połączenie teorii szeregowalności z klasycznymi metodami synchronizacji transakcji umożliwia utrzymanie bazy danych w stanie spójnym i poprawnym.
Klasyczne metody synchronizacji można podzielić na dwie grupy:
Pierwszym narzucającym się pomysłem na zapewnienie ochrony spójności jest zastosowanie mechanizmu blokowania przez transakcje dostępu do obiektów ( relacji, wierszy, pól, itd.) w bazie danych.
Najprostszym rodzajem kontroli współbieżności jest blokowanie binarne. Polega ono na skojarzeniu z każdym obiektem bazy znacznika wskazującego na zezwolenie na dostęp do obiektu lub jego brak. Znacznik taki jest rekordem postaci <id obiektu bazy, stan blokady>. Każda transakcja, chcąca wykorzystać wartość danej X, musi zawierać w swojej treści polecenia wykonania operacji LOCK(X) i UNLOCK(X). O tym czy transakcja otrzyma prawo dostępu do obiektu, decyduje proces systemu zarządzania bazą danych nazywany menadżerem blokad (lock manager). Postępuje on według następującego algorytmu:
jeżeli LOCK(X)==0 //tzn. obiekt nie jest zablokowany przez inną transakcję
to LOCK(X)=1 //tzn. zablokuj obiekt
w przeciwnym przypadku
czekaj aż LOCK(X)==0 //obiekt zostanie odblokowany
oraz menadżer blokad wznowi wykonywanie transakcji
//transakcja jest ustawiana w kolejce transakcji
//oczekujących na pożądany zasób (dane bazy)
LOCK(X)=0 //tzn. odblokuj obiekt
Jeśli inne transakcje czekają na dostęp do X, wybierz jedną z nich i wznów jej działanie.
Aby zapewnić poprawność procesu blokowania binarnego, każda transakcja T musi stosować się do poniższych reguł:
Zadanie stosowania reguł 1, 3 i 4 przejmuje na siebie właściwie funkcjonujący menadżer transakcji, natomiast reguła 2 musi być przestrzegana przez programistę aplikacji systemu bazodanowego. Efektem niezastosowania reguły 2 będzie niepotrzebne blokowanie obiektu, uniemożliwiające realizację wszystkich transakcji chcących z niego skorzystać.
Przestrzeganie reguł 1-4 uniemożliwia jednoczesne użycie tego samego obiektu przez dwie transakcje i stąd chroni bazę utratą spójności danych. Transakcje wykorzystujące różne obiekty bazy mogą funkcjonować równolegle i bezkolizyjnie.
Mechanizm blokowania binarnego, opisany powyżej jest prosty w implementacji. Jednakże konieczność całkowitego blokowania obiektu nawet gdy transakcja wymaga jedynie odczytu, może powodować długie kolejki transakcji oczekujących na dostęp oraz sprzyja powstaniu zakleszczenia (opisane w dalszej części).
Ulepszeniem powyższej metody jest mechanizm oddzielnego blokowania zapisu i odczytu.
W metodzie tej możemy wyróżnić dwa rodzaje blokad:
Zależności pomiędzy poszczególnymi trybami zamykania możemy przedstawić w tabeli:
T1 ↓ T2→ |
READ_LOCK(X) |
WRITE_LOCK(X) |
READ_LOCK(X) |
dozwolony |
niedozwolony |
WRITE_LOCK(X) |
niedozwolony |
niedozwolony |
Jak widać blokada do odczytu przez jedną transakcję nie wyklucza możliwości zastosowania takiej samej blokady na tym samym obiekcie przez inną transakcję.
Realizację programową opisanego sposobu blokowania, możemy zapewnić poprzez wykorzystanie rekordów postaci <id obiektu bazy, stan blokady, ilość blokad odczytu>.
Pole stan blokady może przyjmować trzy różne wartości (odpowiednio zakodowane):
zablokowane_do_odczytu, zablokowane_do_aktualizacji, niezablokowane.
Algorytmy blokowania podano poniżej:
READ_LOCK(X):
b: if lock(x)==”unlocked”
then { lock(x) = „read-locked”; no_of_reads(x) = 1; }
else if lock(x)==”read-locked”
then no_of_reads(x) = no_of_reads(x) + 1;
else { wait until lock(x)==”unlocked” and lock_manages wakes up the
transaction;
goto b: };
WRITE_LOCK(X):
b: if lock(x)==”unlocked”
then lock(x) = „write-locked”;
else { wait until lock(x)==”unlocked” and lock_manages wakes up the
transaction;
goto b: };
UNLOCK(X):
if lock(x)==”write-locked”
then { lock(x) = „unlocked”; wake up one of waiting transactions if any; }
else if lock(x)==”read-locked”
then { no_of_reads(x) = no_of_reads(x) - 1;
if no_of_reads(x)==0
then { lock(x)=”unlocked”;
wake up one of waiting transactions if any; }
};
Obie blokady: zapisu i całkowitą usuwa operacja UNLOCK. Analogicznie jak dla blokowania binarnego, transakcja musi przestrzegać reguł:
Algorytm sprawdzania szeregowalności harmonogramu S z blokadami zapisu i całkowitymi, opiera się na konstrukcji grafu zorientowanego G, w którym wierzchołki odpowiadają transakcjom, a krawędzie wyznacza się korzystając z następujących reguł:
Szeregowalność harmonogramu rozstrzygamy sprawdzając istnienie cykli w tak skonstruowanym grafie (nazywanym również grafem pierwszeństwa). Jeśli G zawiera cykl, to harmonogram S nie jest szeregowalny.
Twierdzenie. Przedstawiony algorytm sprawdzania szeregowalności w poprawny sposób stwierdza szeregowalność harmonogramu.
Dowód poprawności powyższego algorytmu znajduje się m.in. w książce J.D Ullman „Systemy baz danych”.
W przypadku acyklicznosci grafu G harmonogramu S, możemy otrzymać sekwencyjne uporządkowane transakcje według następującego algorytmu:
Przykład. Dany jest graf pewnego harmonogramu dla transakcji T1, T2, T3, T4,T5:
Z powyższego grafu możemy otrzymać wiele harmonogramów sekwencyjnych np.:
Przykład. Przykład harmonogramu nieszeregowalnego. Dany jest harmonogram:
|
T1 |
T2 |
T3 |
T4 |
|
|
Write_lock A |
|
|
|
|
|
Read_lock B |
|
|
|
Unlock A |
|
|
Read_lock A |
|
|
|
|
|
|
|
Unlock B |
|
|
|
Write_lock B |
|
|
|
Read_lock A |
|
|
|
|
|
Unlock B |
|
|
Write_lock B |
|
|
|
|
|
Unlock A |
|
|
|
Unlock A |
|
|
|
|
|
|
|
Write_lock A |
|
Unlock B |
|
|
|
|
|
Read_lock B |
|
|
|
|
|
|
Unlock A |
|
|
Unlock B |
|
|
Graf pierwszeństwa jest postaci:
Ponieważ graf pierwszeństwa zawiera cykle więc nasz harmonogram jest nieszeregowalny.
W przypadku wykrycia cyklu, należy uruchomić mechanizmy cofające efekt działania transakcji T powodującej konflikt, zawiadomić o fakcie program aplikacyjny lub zrestartować T w póżniejszym terminie. Sam mechanizm blokad nie zapewnia szeregowalności dowolnego harmonogramu wykonania transakcji. Stąd też nie gwarantuje utrzymania bazy danych w stanie spójnym.
Gwarancję taką daje zastosowanie protokołu dwufazowego, którego jedynym wymaganiem jest aby transakcje wykonały blokowania wszystkich wymaganych przez siebie obiektów przed odblokowaniem któregokolwiek z nich. Transakcje, które przestrzegają tego protokołu uważane są za dwufazowe w takim sensie, że operacje zablokowania i odblokowania wykonywane są w dwóch różnych fazach w trakcie działania transakcji. Jeśli wszystkie transakcje są dwufazowe, ich równoległe wykonanie zawsze będzie szeregowalne.
Prawdziwe jest następujące twierdzenie.
Twierdzenie. Dowolny harmonogram S transakcji dwufazowych jest harmonogramem szeregowalnym.
Dowód. Przypuśćmy, że tak nie jest. Wówczas z poprawności algorytmu testującego szeregowalność wynika istnienie cyklu Ti1 Ti2... Tip Ti1 w grafie pierwszeństwa dla harmonogramu S. Pewne blokowanie przez Ti2 następuje po jakimś odblokowaniu przez Ti1; Pewne blokowanie przez Ti3 następuje po jakimś odblokowaniu przez Ti2 itd. Na koniec pewne blokowanie przez Ti1 następuje po jakimś odblokowaniu przez Tip . A zatem blokowanie przez Ti1 następuje po odblokowaniu przez Ti1 , co jest sprzeczne z założeniem o dwufazowości Ti1.
ÿ
Zaletą protokołu dwufazowego jest fakt, iż przy niewielkich wymaganiach i stosunkowo niewielkim nakładzie pracy w implementacji, gwarantuje on szeregowalność harmonogramów transakcji.
Wadą natomiast jest to, że blokowanie dwufazowe może ograniczyć współbieżność w bazie danych. Często zdarza się, że transakcja T nie może zwolnić blokady na obiekcie X po jego wykorzystaniu, ponieważ w dalszym planie swego działania przewiduje blokadę na innym obiekcie Y. Aby zwolnić obiekt X, transakcja musi zablokować obiekt Y wcześniej niż jest to wymagane do jej działania. Zablokowanie Y wówczas gdy staje się on niezbędny pociąga za sobą konieczność zbędnego przetrzymania blokady X. W obu przypadkach, obiekt X musi pozostać zablokowany aż do chwili gdy T uzyska wszystkie wymagane blokowania. W tym czasie inne transakcje wymagające dostępu do X są postawione w stan oczekiwania, pomimo iż transakcja T nie korzysta już z X. Jeśli natomiast Y zostaje zablokowane „przed czasem”, działanie transakcji wymagających dostępu do Y jest wstrzymywane, pomimo, że T nie korzysta jeszcze z obiektu Y.
Protokół blokowania dwufazowego zapewnia szeregowalnośc transakcji, ale nie eliminuje możliwości wystąpienia sytuacji zakleszczenia (deadlock) i impasu (livelock), występujących we wszystkich systemach sterujących współbieżnością w oparciu o mechanizmy blokowania. Poniżej przedstawione zostaną przyczynę powstawania problemu i techniki jego eliminacji.
Mówimy, że transakcja jest w stanie impasu, jeśli nie może kontynuować pracy przez nieokreślenie długi ( w stosunku do innych transakcji) czas, podczas gdy inne transakcje są realizowane bez przeszkód. Sytuacja taka może zaistnieć, gdy mechanizm przyznawania blokad (lock manager) nie jest skonstruowany poprawnie i daje pierwszeństwo pewnym typom transakcji. Niestety, praktycznie niemożliwe jest wykrycie impasu w trakcie wykonywania programu realizującego transakcje. Łatwo co prawda zaobserwować, że pewna transakcja czeka bardzo długo na zdarzenie (np. możliwość zablokowania zasobu), które wystąpiło już wiele razy, ale nie wiadomo, jak system zachowa się w przyszłości.
Aby uniknąć problemu, należy zastosować maksymalnie optymalny menadżer blokad. Jednym z takich rozwiązań jest zastosowanie techniki kolejek FIFO: pierwszy-wszedł-pierwszy-będzie-obsłużony. Obsługuje ona transakcje w kolejności zgłoszenia potrzeby zablokowania obiektu. Innym rozwiązaniem jest dopuszczenie różnych priorytetów dla różnych transakcji ale równocześnie wprowadzenie procesu podnoszenia priorytetu transakcjom długo oczekującym na blokadę. Transakcje te mogą w końcowym stadium osiągnąć najwyższy priorytet i dzięki temu mają zapewnioną realizację.
Możliwość powstania tego problemu najlepiej ilustruje poniższa sekwencja działań:
T1 |
T2 |
Lock A |
|
|
Lock B |
Lock B |
|
|
Lock A |
...... |
..... |
Jak widać z powyższej sytuacji ani transakcja T1 ani T2 nie mogą być kontynuowane - występuje zakleszczenie.
Można znaleźć różne strategie zapobiegające powstawaniu zakleszczeń. Przykładem jest strategia wstępnego rezerwowania obiektów (pre-claim strategy). Każda transakcja przed rozpoczęciem działania nakłada blokady na wszystkie obiekty, z których będzie korzystać w trakcie swej realizacji. Taka strategia może jednak powodować, że przy dużym stopniu jednoczesności dostępu (rozumianym jako duża liczba transakcji rywalizujących o zasoby) wiele transakcji będzie musiało długo czekać na rozpoczęcie swego działania. Inną wadą tej strategii jest to, że przed rozpoczęciem realizacji nie zawsze znany jest pełen zbiór obiektów, do których będzie potrzebny dostęp. Taki zbiór może być wyznaczany dynamicznie podczas realizacji transakcji i generalnie może zależeć od danych wejściowych, stanu bazy i algorytmu transakcji. Strategia taka jest więc mało praktyczna w systemach bazodanowych.
Właściwszą metodą wydaje się dopuszczenie możliwości powstawania zakleszczeń ale równocześnie stworzenie mechanizmów do ich wykrywania i eliminowania.
W wykrywaniu zakleszczenia może być pomocne generowanie grafu bieżących transakcji według następującej reguły: jeśli T1 żąda blokady jednostki, która jest zablokowana przez T2, wówczas węzły T1 i T2 łączymy krawędzią.
Sytuacja zakleszczenia odpowiada powstaniu cyklu w grafie. Ilustruje to poniższy przykład:
Detekcja stanu zakleszczenia powinna być wykonywana systematycznie za każdym razem gdy transakcja żądająca dostępu do zasobu, zmuszona jest do oczekiwania. Algorytm wykrywania zakleszczenia polega na rekursywnym przeszukiwaniu grafu oczekiwań w celu odnalezienia ewentualnego cyklu (Ti, Tj). Procedura (w języku Pascal) realizująca to zadanie przedstawiona jest poniżej.
Procedura posługuje się strukturą:
Wait = Record
waited_tran : integer; { id transakcji, na której zakończenie czekamy }
waiting_tran : integer; { id transakcji oczekującej }
End;
Procedure DEADLOCK ( waited_tran, waiting_tran );
Begin
origin := 0;
target := 0;
{sprawdzenie, czy transakcje, na których zakończenie oczekujemy, są transakcjami oczekującymi }
While ( origin < number_of_waiting_transactions ) And ( target = 0 ) Do
Begin
origin = origin + 1;
If ( Wait[origin].waiting_tran = waited_tran ) Then target := origin;
End;
If ( target = 0 ) Then DEADLOCK := FALSE
Else { znaleziono transakcje oczekujące, na których zakończenie czekają inne transakcje }
If ( Wait[origin].waited_tran = waiting_tran ) Then DEADLOCK := TRUE
Else DEADLOCK := DEADLOCK(waiting_tran, WAIT[origin].waited_tran);
End.
Poniżej przedstawiony jest przykład struktury budowanej przez powyższy algorytm:
Wykrycie zakleszczenia powoduje uruchomienie procedur cofających operacje bazy danych do stanu sprzed rozpoczęcia transakcji powodujących zakleszczenie, a następnie ponowne uruchomienie tych transakcji w kolejności gwarantującej uniknięcie zakleszczenia. Wadą tej strategii jest konieczność wprowadzania czasochłonnych procedur utrzymywania (zakładania i zwalniania) zamknięć, konieczność testowania powiązań zbiorów danych będących przedmiotem transakcji i wprowadzenie specjalnych procedur cofania operacji wykonanych na bazie danych. Technika ta może być szczególnie mało efektywna przy wyborze dużego stopnia ziarnistości blokad.
Bibliografia
Spis treści 4
___________________________________________________
1. Pojęcie bazy danych i systemu zarządzania bazą danych 7
___________________________________________________
2. Pojęcie sieciowego modelu danych 14
___________________________________________________
3. Pojęcie relacyjnej bazy danych. 27
___________________________________________________
4. Projektowanie schematu bazy danych. 32
___________________________________________________
5. Metody implementacji schematu bazy danych 49
___________________________________________________
6. Podstawy strukturalnego języka zapytań SQL 56
___________________________________________________
7. Podstawy programowania w strukturalnym języku zapytań PL/SQL. 86
___________________________________________________
8. Transakcje 96
___________________________________________________
Bibliografia 97
___________________________________________________
T1 |
T2 |
READ(X) |
|
|
READ(X) |
X=X-1 |
|
WRITE(X) |
|
|
X=X-2 |
|
WRITE(X) |
T1 |
T3 |
|
sum=0 |
|
READ(A) |
|
sum=sum+A |
|
... |
READ(X) |
|
X=X-1 |
|
WRITE(X) |
|
|
READ(X) |
|
sum=sum+X |
|
READ(Y) |
|
sum=sum+Y |
T1
T4
T3
T2
T1 |
T2 |
READ_LOCK A |
|
READ A |
|
|
READ_LOCK B |
|
READ B |
WRITE_LOCK B |
|
|
WRITE_LOCK A |
T1 i T2 w stanie zakleszczenia
Graf bieżących transakcji dla T1 i T2
T1
T2
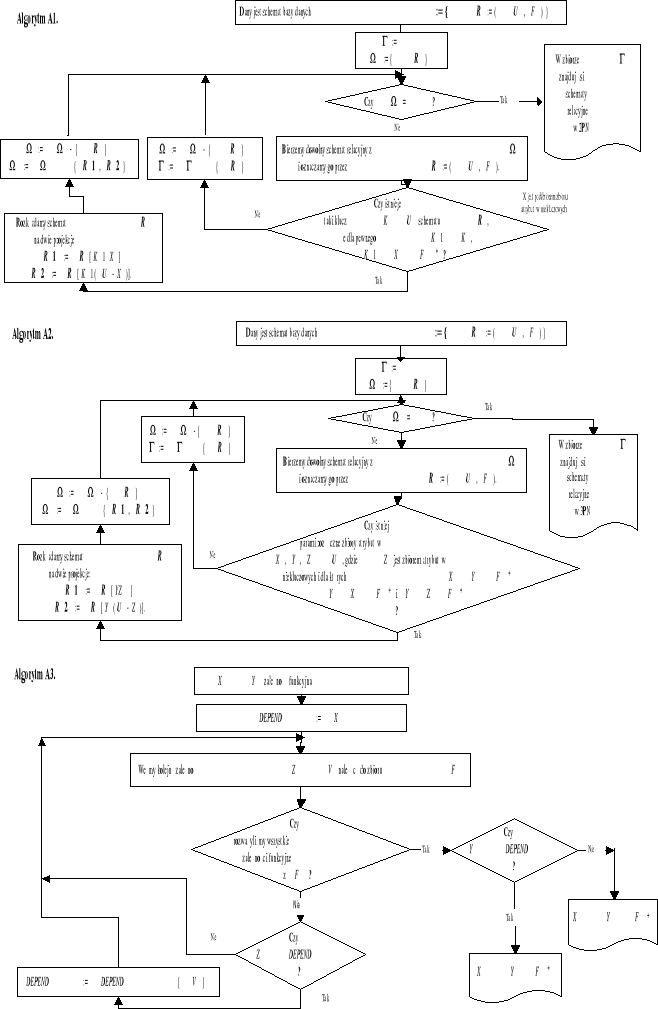
T1
Graf oczekiwań dla powyższych transakcji :
C
B
G
F
A
T3
T2
T5
T4
Wait |
Waiting_tran |
Waited_tran |
|
|
|||||
|
A |
B |
|
|
|||||
|
B |
C |
|
lista transakcji oczekujących |
|||||
|
B |
F |
|
|
|||||
|
F |
G |
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
G |
A |
|
|
||||
|
|
( ten rekord stworzy cykl i wykaże zakleszczenie ) |
|||||||
Wyszukiwarka
Podobne podstrony:
1 Tworzenie bazy danychid 10005 ppt
bazy danych II
Bazy danych
Podstawy Informatyki Wykład XIX Bazy danych
Bazy Danych1
eksploracja lab03, Lista sprawozdaniowych bazy danych
bazy danych druga id 81754 Nieznany (2)
bazy danych odpowiedzi
Bazy danych
notatek pl g owacki,bazy danych Nieznany
BAZY DANYCH SQL (2)
Bazy danych kolo 2 1 id 81756 Nieznany
Projekt Bazy Danych
Microsoft PowerPoint 02 srodowisko bazy danych, modele
in2 modelowanie bazy danych
kolokwium sklepy1, WAT, SEMESTR V, PWD, Bazy danych od maslaka
więcej podobnych podstron