99969

M_u = Me~^u (cos Lr + sin Lx)

(7.122a)

M_K=—e~^Lx%mljc ^R L

Po zsumowaniu lewostronnego i prawostronnego oddziaływania ramy określamy momenty w całej belce (płycie) konstrukcji:

M=M_a e~^u (cos Lx+sin Lx)+ M_a e~^~^x\cos Uf - x)+ sin Uf - *)]+

+ **_e-^usinLx+^e-^I*-')swL(l-x)    f7.122b)

L    L

gdzie: M_A i M_B - momenty podporowe, R_A i R_B - reakcje pionowe, / - rozpiętość obudowy.

Podane rozwiązania można też wykorzystać do obudowy skrzynkowej jako jednej konstrukcji - belki na sprężystym podłożu z nadbudową. Obciążeniem belki jest wówczas oddziaływanie nadbudowy. W dowolnym schemacie metody sil podłoże sprężyste możemy zamienić podporami sprężystymi, wykonując obliczenia metodą Żemocz-kina (rys. 7.47).

LH' I I 1 * i * * > * i i

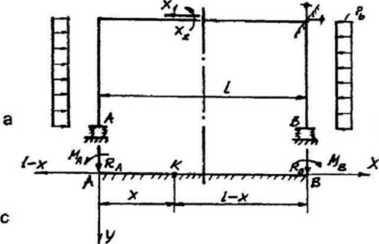
Rys. 7.4Ć. Schemat obliczeniowy obudowy skrzynkowej: a) rama z zastosowaniem metody sil, b) rama z zastosowaniem metody przemieszczeń, c) belka na sprężystym podłożu,

A i B - punkty połączenia ramy z płytką - belką, K - dowolny punkt belki