3289581010

406 Dział czwarty. — Wytrzymałość materyałów.

tf.-A

OBJ

max P

O ~ min

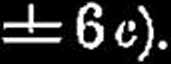
że dla przekroju prostokątnego a * b, gdy b

— 1. mamy:

(JA

a_s 6

_ więc otrzymujemy następujący prosty sposób wykreślania naprężeń, rys. 242. W środku ciężkości S kreślimy SS_X =Os— l*: o prostopadle do B_l} dalej K’S_l aż do r/C"    A    przecięcia się D z siłą P, następnie DA'

i    ! ‘    równolegle do 7J_t A_t, a rzędne punktów pro-

stej A^f S_x ]j wyznaczają nam naprężenia dowolnego punktu przekroju. (Pole naprężeń .4j B_v B' Si A' zakreskowano w rysunku). Ai .4' i Bi JA są naprężeniami skrajnemi (w krawędziach).

ii’ możemy też wykreślić bezpośrednio: Prosta K” 5, przecina siłę P w a EJ? jest równoległa do .1, B_t. Zasada wykreśleń powyższych stosujo się i wtenczas, gdy siła P działa na przekrój poza obrębem rdzenia, o ile tylko pozostaje w osi głównej prostokąta.

9. Dla długich prętów, które ulegają przegięciu bocznemu pod wpływem siły, działającej w kierunku osi. lecz mimośrodkowo, mamy wzory:

Wzór na	Rozciąganie mimośrodkowe (rys. 243)	Ściskanie mimośrodkowe (rys. 244)
Kównanio odkształconej.		« —---—— (1 — cos co x). COS 6) i
Największe przegięcie (boczne).	^ ^P (^1 cosh oj l )	f —L__ A \ COS OJ l }
Moment gnący.	cosh o x * cosh co l Przy x — l będzie:	COS to* M = r w----: ■ ■ ^x cos co / Przy x = 0 będzio: M - ^Fl> ^,nax~ COSOłł ’
Największe naprężenia.	o™ ' i ± "Jy. mm \ -^1- W/	mas f pF a . — o. (1 -f- ----— | • mm * \ W cos cal j

Znaczenie funkcyi hyperbolicznej cosh — patrz str. 67. Ilość 0) zaś ma wartość:

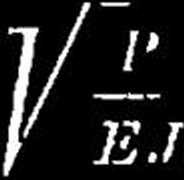
Rys. 243. Rys. 244.

przyczem E oznacza spółczynnik sprężystości w kg/cm⁵, J (w cm⁴) moment bezwładności przekroju F względem osi ciężkości, prostopadłej do płaszczyzny przeginania. II’ oznacza w cm³ moment wytrzymałości przynależny do J.

Wzory przybliżone otrzymamy, podstawiając w powyżej podane wzory wartości przybliżone: