3289581028

II. Wytrzymałość prętów prosty cli. 411

3. Ciągnienie (lub ciśnienie) i kręcenie.

Postępujemy tak, jak wskazano pod 1., zastępując jednakże siłę Q i cięcie proste z_s momentem kręcącym ftfd i powstającem pod jego wpływem kręceniem Zd. Bezpieczne cięcia ku zastępujemy takimiż krę-ceniami kd.

4. Gięcie i kręcenie. *)

Przekrój niechaj podlega działaniu momentu gnącego M, którego płaszczyzna stoi prostopadle na przekroju, i momentu kręcącego Md, którego płaszczyzna jest równoległą do przekroju. Pod wpływem ił/ powstaje w dowolnej cząstce przekroju naprężenie normalne cr, a pod wpływem Md kręcenie z, które oznaczamy oddzielnie podług wzorów i sposobów na właściwem miejscu już podanych, poczem stosujemy wzór zasadniczy, podany pod c (str. 410) z wartością a₀ = kb : 1,8 kd. łącząc w jedno równowarte naprężenie główne eh te, przynależne do siebie wartości a i t, których wynik byłby największością.

1) Przekrój kołowy i pierścień kołowy (rys. 251 i 262). W tych

przekrojach punkty mające dmax mają zarazem i zv\*x, co upraszcza obliczenie. Oznaczmy przez W niezbędny moment wytrzymałości, a więc (p. str. 364, wzgl. 365).

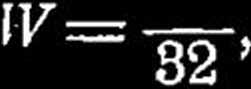
wzgl.

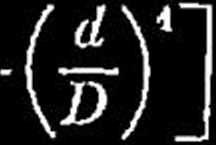
Rys. 251.

a obliczywszy:

Mi = 0,35 M 4- 0,65 J/li*

(«o Md)²,

oznaczymy:

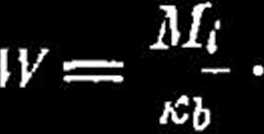
* d*

2) Przekrój eliptyczny (rys. 253). Moment gnący iii" rozkładamy na Mi, obracający około osi 1 i M_t około osi 2.

Dokładne wyliczenie największego naprężenia głównego jest mozolne. **) Dla określenia przekroju wystarcza obliczenie wielkości h i b z poniższych dwóch równań:

___Rys. 253.

— bPkb> Mi' = 0,35 Ml h- 0,65}/ Mi' + (o₀ Md)*,

— b-h ki> Mi” = 0,35 M₂ -+- 0,65 J/M₂- -h (ct₀ Md)²,    J.

w których wartość: o₀ — kb : 1,3 kd.

Największe naprężenia zachodzą równocześnie w 4-ech punktach obwodu, leżących nie w końcach osi głównych 1 lub 2, lecz między nimi.

■) Dla przekroju I p. E. Haeseler, Centralbl. d. Bauvenv. 1895, str. 233 i 231. **ł C. v. Bach — Elasticitftt und Festigkeit, 3 wyd. Berlin 1S98, J. Springer.