5027720117

Modelowanie Matematyczne w Fizyce i Technice

STATYSTYKA PROCESÓW NISZCZENIA W UKŁADACH NANOFILARÓW ZE STOCHASTYCZNYM TRANSFEREM OBCIĄŻENIA

Tomasz Derda

Instytut Matematyki, Politechnika Częstochowska, Częstochowa, Polska tomasz.der da @im. pcz.pl

Korzystając z idei modelu wiązki włókien (ang. Fibrę Bundle Model) zbudowano model matematyczny niszczenia układów nanofilarów poddawanych obciążeniu osiowemu. Rozmieszczone w węzłach sieci nanofilary charakteryzują się indywidualnymi progami wytrzymałości na ściskanie cr_lh. Progi wytrzymałości losowane są zgodnie z wybranym rozkładem prawdopodobieństwa. Zastosowano dwa rodzaje rozkładów o gęstościach:

gdy<7₀<<7_th,

w przeciwnymprzypadku,

(1)

p(^)={^p<ex^°^P_<^

oraz

pf^.h)

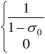
gdy cr₀ < <7_[h < 1, w przeciwnymprzypadku.

(2)

Wzór (2) odnosi się do rozkładu równomiernego na przedziale [cr₍₎,l]. Dla <x₀=0 wzór (1) jest funkcją gęstości prawdopodobieństwa rozkładu Weibulla z indeksem Weibulla p . Przyjmując cr₀ >0 uzyskuje się rozkład obcięty poniżej

<T₀.

Rozważane są dwa sposoby obciążania układów nanofilarów: qu as i-statyczny oraz poprzez zastosowanie skończonej siły F . Pod wpływem obciążenia przekraczającego próg wytrzymałości danego filara ulega on zniszczeniu. Obciążenie pochodzące ze zniszczonego filara jest transferowane do innych nieuszkodzonych filarów w układzie. W prezentowanym modelu obciążenie jest redystrybuowane w sposób losowy do najbliższych nieuszkodzonych sąsiadów zniszczonego filara. W literaturze znane są dwa inne przypadki zastosowania stochastycznego transferu obciążenia [1,2].

Prawdopodobieństwo zniszczenia układu w zależności od zadanego obciążenia cr można dopasować za funkcji:

18