30909592

IKilIHT V«l % łnrii IKM I'>

I. ktnrt tf <«Urt (<il*nwv/

A. ww/yMkle hti irdjl ąn» nt\ niw/io, tn <i(k/•• wuv*łkt* W Mv w r<w H, ji-łli tn/ytikir kąty trójkąta M równe, 10 l»k»e n^yMUf irg" boki m ( . JoAll iw/MłlWf bola czworokąta «ą równe. U) 1aW/<• wi/.ytukw Kr." Mty *•»! rOwn» rj, |r-jitl wszystkie kąty rawnrdM* m proste. lu i zworókut t*n |e*t prontokątem

i!. Dtojuwra przekątna rumbu dzieli no nn dwu trójkąty

A. prostokątne B. równoboczne C. równoramienne o. o kątach «»". io*. IW

i AHC są

o

h

3.    W czworokącie AtU O |AB< - IBCI I IHG - IAPI- Itójkąty ACH

A. promokntnr    C. przystające

B. równoramienne    D. równoboczne

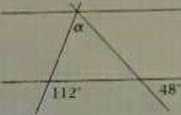
4.    Proste o I b na rysunku są równolegle. Kąt n ma miarę:

A,56* B. Ii4° C.{łO* D. 20°

5. Narysuj kąt rozwarty *t uraz odcinki u i b. Skonstruuj trójkąt o. bokach a i b i kącie « zawartym miedzy nimi.

6. W trójkącie AHC kąt ACH ma młace 64^a. a kąt 8 AC - 36". 7. wierzchołka £' poprowadzono wysokość¹

8. Oblicz pole czworokąta n wirrzdioIJcadi A * (-5, -1), B «(1, -1), C- (1.5M D - l-S, r.).

ROdm

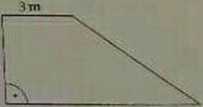
9. tatą powierzchnię działki w ks&otcfe trapezu o wyrmaradi przedstawionych aa rysunku obsiuno trawą, lic opakowań nasion trawy kupiono, jczeh jedno opakowanie wystarcza na obstanie 3 nv' powierzchni?

JO. Jeden metr kwadratowy' pewnej wykładziny kosztuje iS zl. Szerokość lej wykładziny wynosi l,5ra. Czy 200 zi wystarczy mi zakupienie 23 metra bieżącego tej wykładziny?

V

l. Dany jest trapez A li CD, w' którym Aft \} CD. Na podstawie AR zaznaczono punkty £ t r taki**, ze "It AD l FD II nc. wykaz, 7.0 czworokąty AFCD 1 FflCD mają równe pola.