4663671137

Niepewność obliczania średniej pomiarów (z uwzględnieniem współcz. Studenta-Fishera dla n=5):

n

E (Xi - x)‘¹

i= 1

«(<i°r» = \ ^7—TT \ n(n — 1)

• 1,141

Niepewność obliczania okresów i ich kwadratów:

u(T) =

tt((10 T))

10

u(T¹) = u(T) ■ 2 ■ T

u«10T». s	u(T), s	u(T-), s~
0,001909	0,0001909	0,0004195
0,000807	0,0000807	0,0002048
0,000807	0,0000807	0,0002395
0,002212	0,0002212	0,0007141
0,001229	0,0001229	0,0004114
0,001930	0,0001930	0,0006906

Niepewność wyznaczania współczynnika kierunkowego regresji liniowej (n=6):

«(«) =

r

„    ---72> e_i = y_i-ax_i-b

n E A - ( E Xi

a=l

m

u(a) = 0,0124

Przyspieszenie ziemskie liczone ze współczynnika kierunkowego (7) jest zależne od jednej wielkości niedokładnej, a. Zgodnie z prawem propagacji niepewności:

«(flO =

°⁹ i \

d~a '^U{a)

2

47T

2

a

2

u(a)

47T

2

4,0064¹

—^ • 0,0124 = 0.030498

u(g) = 0,030

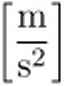
5 Wynik końcowy i Wnioski

przyspieszenie ziemskie

g

9,854(30)

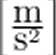
Tablicowa standardowa wartość przyspieszenia ziemskiego wynosi 9,80665-^ (w zależności od szerokości geograficznej 9,78^-9,82). Zgodnie z empirycznym wzorem¹, na szerokości geograficznej 50°17' i wysokości 200 m n.p.m. przyspieszenie ziemskie wynosi ok. 9,81-^f.

Po uwzględnieniu niepewności rozszerzonej (±0,060) wynik (9,794 ± 9,914) zgadza się z wartością oczekiwaną.

Przyczyną różnicy może być niedokładność odwzorowania modelu wahadła matematycznego w rzeczywistości (kulka nie jest punktem materialnym, nić nie jest nierozciągliwa i nieważka), użyte przybliżenie małych kątów lub niewłaściwa płaszczyzna drgań.

Ponadto jeśli liczyć g osobno dla każdej długości wahadła okazuje się, że wyniki są zawyżone dla L większych niż 0,5m. Sugeruje to występowanie jakiegoś błędu systematycznego dla pomiarów przy większych długościach.

3

1

jak podanym na: http://pl.wikipedia.org/wiki/Przyspiaszenie_ziemskie