2212791163

EKONOMIft MENEDŻERSKA

Wykład 3 Funkcje produkcji 16

Warunek optymalnej techniki produkcji można również uzyskać wykorzystując metodę mnożników Lagrange’a:

Zadanie optymalizacji:

J PkK + PlL -> min \ Q(K,L) > Q₀

Funkcja Lagrange’a:

LF = - p_K K - pi L + ( Q(K, L)-Qq)u u - mnożnik Lagrange’a

Przyrównujemy cząstkowe pochodne funkcji Lagrange’a do zera:

r

8LF

dK

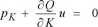
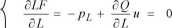
rtj F

^?=-= Qo-Q(.K,L) = o

Wykorzystując definicje krańcowych produkcyjności czynników otrzymujemy:

PK = ^mpk "

•\ Pl = MPl "

Q(K,L) = G„

Po podzieleniu stronami i przekształceniu otrzymujemy znany już warunek:

MP_k _ MP, Pk    Pl

Irena Woroniecka

Wydział Informatycznych Technik Zarządzania Wyższa Szkoła Informatyki Stosowanej i Zarządzania