4736386899

°_ PRÓBNA MATURA2006

Matematyka Arkusz II - PEŁNE rozwiqzania zadań. 17 listopada 2006

POZIOM ROZSZERZONY

Czas pracy 180 minut

ZADANIE 1. (5 pkt)

Funkcja homograficzna/jest określona wzorem /(x) = ———, gdzie pei jest parametrem

x-p

i \p\*S.

a)    Dla p = 1 zapisz wzór funkcji w postaci f(x) = k+ —ⁿ—, gdzie k oraz m są liczbami rzeczywistymi

b)    Wyznacz wszystkie wartości parametrup, dla których w przedziale (/?, + «) funkcja/jest malejąca.

ZADANIE 2. (5 pkt)

Wyznacz wszystkie wartości k e R, dla których pierwiastki wielomianu W (x) = (x² - 8x + 12) • (jc - k) są trzema kolejnymi wyrazami rosnącego ciągu geometrycznego

ZADANIE 3. (4 pkt)

Na rysunku poniżej przedstawiono wykres funkcji logarytmicznej/

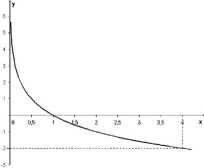
Rozwiąż równanie (/(x))² -16 = 0.

© CKA 2006. Plik pobrany ze slrony www.zadania.pl - Matematyka - rozwiązania zadań Arkusz II