490575044

53

Obliczenia hydrauliczne przepławek dla ryb

4 hd_n

K=-^CWR    (¹³)

Wy

gdzie (11-13):

A_r - pole przekroju poprzecznego pojedynczej rośliny [m²],

A_v - pole powierzchni obszaru zajmowanego przez rośliny (B x L) [m²],

n - liczba łodyg (szczotek),

d_p - średnica pojedynczej rośliny [m].

Jak wynika z analizy równań (11), (12) i (13), problem określania współczynników oporów X_R sprowadza się do poprawnego wyznaczenia współczynnika oporów kształtu c_WR - pojedynczego elementu wśród grupy roślin i określeniu ich rozstawy: w kierunku przepływu a_x oraz prostopadle do niego a Lindner do obliczania współczynnika c_WR podaje zależność, którą do celów praktycznych wygodnie jest stosować w modyfikacji Rickerta:

gdzie:

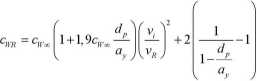
(14)

c_wx - współczynnik oporu pojedynczego elementu roślinnego,

( _v A względna prędkość dopływu do elementu roślinnego, zależna głównie od — - długości (a_NL) i szerokości (a_m) ścieżki wirowej Karmana za opływaną łodygą.

Przy opływie elementów roślinnych tworzą się tzw. bezwładnościowe fale stojące, które powodują dodatkowy wzrost oporów kształtu. Wpływ ten uwzględnia drugi człon równania (14). Charakterystykę oporów przepływu w przepławce z zabudową roślinną X_R należy uzupełnić formulą uwzględniającą opory tarcia na dnie i skarpach kory ta X_D. Zadowalającą dla celów projektowych dokładność zapewnia modyfikacja równania Colebrooka-White'a podana przez Paschego:

1

= 2 log

14,84fl_łD')

K.o )

(15)

Do oszacowania zastępczej szorstkości piaskowej dla dna skarp koryta k_sD pomocne mogą być podręczniki inżynierskie. Można również wykorzystać znajomość współczynnika szorstkości n (tutaj n_D) we wzorze Manninga. Według Garbrechta pomocna jest następująca zależność:

(16)

1 _ 26

»D k)',D

Formatio Circumiectus 9 (2) 2010