7716655329

j ₌ LnL_eJYl -i._ejvi

" V2

wR(t) = U_Rmsm(cot + \f/_u) => U_R=^^-e^JV/U ₌u_R.e^JV/u Z zależności | ^    wynika:    Un =U_R -e^^u = R-I-e^I =R-I

W-^/=o

i(t) = I_m sin(cot + i/j)

Jest zatem:
ur=r-l	(7.3a)
a po przekształceniu:
I = —U„=GU„ - R -R -R	(7.3b)

Są to dwie dualne postacie zależności zwanej prawem Ohma w postaci symbolicznej dla rezystora poddanego wymuszeniu sinusoidalnie zntiennemu.

Odpowiadający powyższym zależnościom wykres wskazowy napięcia i prądu rezystora pokazano na rys. 7.3.

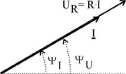
Rys. 7.3. Wykres wskazowy napięcia i prądu rezystora idealnego

Rys. 7.2. Rezystor - schemat zastępczy do metody symbolicznej

Impedancja, admitancja i rezystora wynoszą:

kąt przesunięcia fazowego odbiornika złożonego z idealnego

I I - U_R

Stąd impedancja i admitancja zespolone:

, _V-r RL „ „    1

~-

/.R =

<p=Tu—

■=**.*,

I

— =G R

Z prawa Ohma wynika, że wartości chwilowe prądu i napięcia na rezystorze są do siebie wprost proporcjonalne w każdej chwili czasowej, a więc mają przebiegi czasowe równokształtne. Wykorzystuje się to przy pomiarze prądu, a zwłaszcza przy jego wizualizacji za pomocą oscyloskopu elektronicznego.

Przebiegiem okresowym jest także przebieg czasowy wartości chwilowych mocy z jaką rezystor zamienia energię elektryczną na energię cieplną. Wartości chwilowe mocy rezystora są równe iloczynowi wartości chwilowych napięcia i prądu -PR(t) = u_R(t) i(t). Po podstawieniu do tego wzoru wyrażeń na przebiegi chwilowe prądu i napięcia otrzymuje się:

Lr=~.

4R

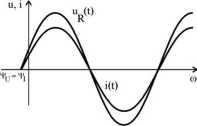
Rys. 7.4. Przebiegi czasowe napięcia i prądu rezystora

PR (0 ⁼    • U_R sin(at + ipj )■ -J~2 • I • sin(cot + i//j ) =

= 2-U_RI ■ sin²(cot + ip_I) = U_RI [l-cos2(at + y/j )]

-20-