1109810387

ty leżące w sąsiedztwie lub w niewielkiej odległości z wysokim prawdopodobieństwem powinny należeć do tego samego obiektu, a więc do tej samej klasy. Ta prosta obserwacja stanowiła inspirację do zaprojektowania algorytmu klasyfikacji uwzględniającego zarówno podobieństwo w przestrzeni cech jak i zależności geometryczne.

Zaproponowany algorytm używa klasyfikatora 1-NN (czyli metody stosunkowo wolnej, nawet po redukcji zbioru uczącego, która zresztą została przeprowadzona) tylko dla niektó-lych pikseli obrazu. Pozostałe piksele przechodzą do drugiego etapu, w któiym w pierwszej kolejności rozpatrywane jest kryterium związane z otoczeniem punktu i na jego podstawie podejmowana jest decyzja o przynależności piksela do określonej klasy. Dopiero w przypadku, gdy kiyterium to nie daje wystarczającej pewności, punkty są przetwarzane przez klasyfikator 1-NN. Idea klasyfikacji wieloetapowej (tzw. klasyfikatoiy kaskadowe) jest powszechnie stosowana w dziedzinie rozpoznawania obrazów dla przypadku ogólnego. W wypadku zadania klasyfikacji pikseli takie podejście może zasadniczo skrócić czas obliczeń kosztem niewielkiego, być może niezauważalnego spadku jakości segmentacji, pod warunkiem właściwego dobom schematu klasyfikatora. Z uwagi na brak miejsca nie możemy dokładnie opisać zbadanych wariantów naszkicowanego podejścia, pokazujemy jednak na Rys. 3 metody podziału płaszczyzny na punkty klasyfikowane w pierwszym przebiegu przy pomocy zbiom uczącego oraz te, które mają szansę być sklasyfikowane bardzo szybko, korzystając z informacji już o wynikach klasyfikacji ich sąsiadów . Eksperymenty pokazały, że wykorzystanie sąsiedztwa geometrycznego przy klasyfikacji powoduje rozbieżności w podejmowaniu decyzji dla tylko ok. 1-2% pikseli w stosunku reguły 1-NN (ze zredukowanym w obu przypadkach zbiorem odniesienia) zastosowanej do wszystkich pikseli, natomiast osiągnięte przyspieszenie klasyfikacji jest 2-3-krotne.

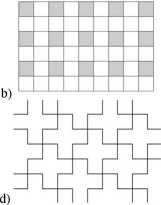
Rys. 3 Zbiory klasyfikowane w pierwszym przebiegu: (a) szachownica, (b) punkty kratowe, (c) punkty kratowe zmodyfikowane. Część (d) pokazuje, że “krzyże” pokrywają całą powierzchnię siatki prostokątnej.