1492317403

1. Introduction

The assessment of solidity of implants for dentistry applications reąuires the study of peculiarities of their deformation [1]. Determining of the plastic deformations in select zones of implants with greatest local tensions can serve as an effective criterion of the degree of deformation of implants and structural elements.

The assessment of the critical bending of an implant under one-point mechanical pressure was undertaken with the aid of two methods: the shadow method and the optical-digital speckle-correlation (ODSC) method [2]. With the aid of the shadow method in non-coherent optical system a shadow image of the implant is formed and, by bending it back and forth, a bending angle behind the image rims is controlled. However, this method does not allow to assess distribution of deformations on the surface of the implant during its bending and, thus, to determine the critical bending. On the other hand, with the aid of ODSC method a distribution of the fields of shifts and deformations over the entire surface of the implant can be built. Application of this method enables to find segments with emerging plastic deformations during the implant bending. As a result, the study of distribution of deformations over the entire surface, in particular, at the segment of its maximal bending, one can establish the deformation values critical for the start of the process of destruction of the implant materiał.

2. Choice and optimization of parameters of the implant image formation systems

A series of studies of implant samples manufactured from titanium alloy BT-16 were conducted with the aid of experimental eąuipment based on a non-coherent optical shadow implant shadow images formation system, as well as the optical speckle-images formation system.

2.1. Non-coherent optical shadow implant shadow images formation system

Formation of shadow images of bodies of spherical, conical and cylindrical shapes has certain properties. For example, practical dentistry employs complex implants containing cylindrical and conical shapes. For this reason, during formation of shadow images one must ensure that the dimensions of aperture D of the projection lens would

not be less than the expected size (diameter) of the object, in other words, d = — ;> a ₀

f_#

, where d₀ is the expected size (diameter). If vice versa, d = f / f < a ₀, then the lens will not build images of the entire cylinder, cone or sphere but only those their parts with d₀ diameter from which the rays fali into the lens aperture (see figurę 1). The real diameter d₀ of the cylinder, sphere or cone and diameter dj of those their parts whose image is formed with the lens, are connected by a function [3]:

a

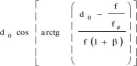
9

0)