1935182607

18

SPIS TREŚCI

Niech lim a„ = a > O i niech O < e jest takie, że O < a — e, to (a — e)^bn < a*" < (a + e)⁶ⁿ.

Niech S = {x G R : 3(fc_n)^₌₁ lim aj£ⁿ = x} będzie zbiorem punktów skupienia ciągu a^ⁿ, to wtedy dla każdego e > O i każdego x € S istnieje podciąg ciągu a^b" zbieżny do x 6 S a wtedy

(a-c)^b= lim (o - e)^bkn < lim oj*- = i < lim (o + e)**- = (o + ef.

Więc ostatecznie dla każdego e > 0 mamy:

S c((a-E)‘,(o + e)‘).

Niech e_n := dla każdego n € N to wtedy

lim (a + e„)⁶ = a⁶ lim (l + ^ = a^b lim ^1 + ^ ^    < a^b lim 3" = a^b lim '!/& = a⁶l = a⁶.

Hm (o - e„)‘ = ‘‘i (l - 7)'' = „ta ((l -    ") " >    “S,    = “*■

Stąd ostatecznie mamy

0 ? S C f| [(o - *)*, (O + e)¹] c fl [(o - £„)», (a + e„)‘] = {a¹}.

£>0    n£N

Więc zbiór punktów skupienia ciągu a£" jest jednoelementowy S = {a⁶}, co dowodzi, że lim a^ⁿ = a^b, co kończy dowód p-ktu 5-tego. ■

Twierdzenie 0.3.8 Jeśli ciąg lim = g € R, to

2. jeśli On>0 to lim

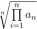
= 9•