262080648

Uniwersytet Ekonomiczny w Krakowie

(X^TXr‘X^TXb = (X^TX)-'X^Ty = b = (X^TX)-‘X^Ty

oraz

—- = 2X^tX jest macierzą określoną dodatnio, zatem spełniony jest też warunek

c.b.d.o.

dostateczny istnienia minimum funkcji S(P).

Własności estymatora MNK;

a)    estymator b jest estymatorem liniowym (tzn. jest kombinacją liniową wektora y, obserwacji na zmiennej zależnej, tj. b = C^Ty)

b)    estymator b jest estymatorem NIEOBCIĄŻONYM (tzn. E(b) = P)

c)    macierz kowariancji wektora b dana jest wzorem: V(b) = o²(X^TX)'¹

d)    Twierdzenie Gaussa-Markowa:

Wektor ocen parametrów strukturalnych b, uzyskany za pomocą MNK, jest najefektywniejszym (tzn. ma najmniejszą wariancję) w klasie nieobciążonych estymatorów liniowych.

Oznacza to, że dla każdego innego estymatora liniowego nieobciążonego, powiedzmy a, takiego że a = C^Ty i E(a) = P, różnica: V(b) - V(a) jest macierzą określoną niedodatnio.

W myśl twierdzenia Gaussa-Markowa estymator MNK jest najlepszy (najefektywniejszy) wśród wszystkich estymatorów liniowych nieobciążonych. O takim estymatorze mówi się, że ma własność BLUE (best linear unbiased estimator).

Twierdzenie

W KMNRL estymator MNK ma K-wymiarowy rozkład normalny, tj: b ~ Nk(P, o²(X^tX)‘¹)

Twierdzenie

Nieobciążonym estymatorem wariancji składnika losowego o² jest tzw. WARIANCJA RESZTOWA S_e² dana wzorami:

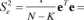
N-K

^e'^e=(y - y)' (y - y)=(y - ^Xb)' (y - ^Xb>

;(y^ry-b^rX^ry)

gdzie: N K

N K e = y-y y = Xb

—    liczba obserwacji

—    liczba szacowanych parametrów

—    liczba stopni swobody

y    — wektor reszt

>    — wektor wartości teoretycznych

Odpowiedni zapis skalamy wariancji resztowej ma postać:

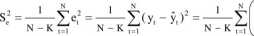
K

2

Ekonometria, Antoni Goryl, Anna Walkosz strona 8