6815960222

zaś w obszarach V i VI zachodzi

(5.43)

(5.44)

(5.45)

*,(<) = *r ('),

xM=-h(t)/T_r,

ÓX2(t)/ÓX_t(t) = -VT_p.

Rozwiązania równań (4.39), (4.42) oraz (4.45) mają postać, odpowiednio:

*l(0 = -r_pz₂(r) -Bk_pT_p • ln|-Bk_p + xę,(z)|+C_(z₀),    (5.46)

C_«o) = *i('o) + T^ilo) + Bk_pT_p M-Bk_p + Zj(<„)|,    (5.47)

III i IV :

*l(0 = -T_p*2(t) + BkpTp • ln|Bkp +    .    (5.48)

C+('o) = ^i('o) + TptzCo) - Bk_pTp ■ ln| Bk_p + z₂(/„)|,    (4.49)

V i VI :

Xi(t)=-T_pK₂(t) + Q,(k_>),    (5.50)

Co(^to) ^{= x}l(^lo)⁺T_pX2(lo).    (5.51)

Stan równowagi badanego układu odpowiada zależnościom:

x₂(0 = 0 oraz u(t) = 0.    (5.52)

Na płaszczyźnie fazowej jest to odcinek x₂(t) = 0 oraz -a <x_l <a. W zależności od wartości parametrów obiektu k_p oraz T_p, a także charakterystyk przekaźnika, w układzie może także wystąpić stabilny cykl graniczny.

5.3 Sterowanie w układzie przekaźnikowym z korekcyjnym podatnym sprzężeniem zwrotnym

Strukturalny schemat badanego układu sterowania, w którym zastosowano liniowe korekcyjne sprzężenie zwrotne podatne pokazano na rys. 5.9.

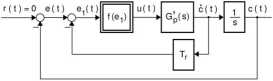
Rys. 5.9. Strukturalny schemat układu sterowania z korekcyjnym sprzężeniem

Schemat ilustrujący zasadę praktycznej implementacji omawianego sprzężenia w przypadku sterowanego obiektu całkująco-inercyjnego (5.1) podano na rys. 5.10.