7025752575

Wykład 1. Metody numeryczne - równania liniowe

W każdej «-tej kolumnie element przekątnej wyznaczany jest ze wzoru:

m—i

(1.20)

Lmm ⁼ \ Ajm ~ ^ik^mk \    k=1

a pozostałe z zależności:

Lim ~

Aim Lk=l LikL_mk

(1.21)

(1.22)

Efektem dekompozycji jest układ równań: LL^Tx = b

, który jest rozwiązywany w dwóch etapach. Pierwszy,prowadzony jednocześnie z dekompozycją, polega na rozwiązaniu układu:

(1.23)

U = b

Elementy wektora £ wyznaczane są na podstawie równań:

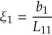
(1.24)

(1.25)

fy LU ^jkźk

Po dekompozycji wektor rozwiązań x wyznacza się na podstawie równania:

L^tx = £    (1.26)

analogicznie jak w przypadku metody eliminacji Gaussa-Jordana

Warunkiem zastosowania tego algorytmu jest symetria i dodatnia okre-śloność macierzy współczynników A. Taka postać macierzy współczynników towarzyszy analizie większości realnych zagadnień.

1.0.5. Algorytmy pasmowe i frontalne

Niektóre zagadnienia, takie jak analizy metodą elementów skończonych, wykorzystują rzadkie macierze współczynników, które powstają poprzez złożenie niewielkich pełnych macierzy i wektorów [?,?].

W takim przypadku obliczenia prowadzi się w trzech etapach. Pierwszy polega na wyznaczaniu owych niewielkich, pełnych macierzy składowych, drugi - na złożeniu tych macierzy i wektorów w jeden układ, który w trzecim etapie jest rozwiązywany jedną z metod przedstawionych wyżej.

Algorytmy tego typu są przydatne w analizie układów, których wymiar macierzy współczynników nie pozwala na prowadzenie operacji na całej macierzy. Proceduralnie algorytmy różnią się od poprzednich jedynie sposobem organizacji obliczeń oraz wykorzystania pamięci operacyjnej.

Metody stało- i zmiennopasmowe korzystają z własności struktury macierzy rzadkiej. Szerokość pasma macierzy m określona jest w oparciu o wymiar fragmentu wiersza otoczonego zerowymi elementami. Istotną