70520493

11. Uzasadnić, że podane funkcje są równowartościowe na wskazanych zbiorach:

(a) f(x) = 2x — 3, M;    (b) f(x) = —,    (0, oo).

x

12.    (P) Korzystając z własności logarytmów obliczyć:

(a) log₆ 3 + log₆ 12; (b) log₃ 18 - log₃ 2;    (c) 9 log₆ v^/36;

(d) 3 log₂ 3 ■ log₃ 4; (e) 3 log₄ 73 - ^ log₄ 3 + 3 log₄ 2 - log₄ 6; (f)    27 - lofe 9'

13.    Naszkicować wykresy funkcji:

(«) y = (i + l)⁴;    (b) y =    (o)    y    =

(d)    y = 2^X+1;    (e)y=Q)^a:2;    (f)    y    =    #1;

(g) y = 5 + log₂ x\ (h) y = |log 100x|; (i) y = logi -y •

14.    Znaleźć funkcje odwrotne do funkcji:

(a) f(x) = y-j-;    (b) f(x) = 3 - 7x + 2; (c) f(x) = 2^X_1; (d) f(x) = 4^X ;

(^e) f{x) = log(:r + 2); (f) f(x) = x² {x < 0;    (g) f(x) = 73 - x (x < 3).

Lista 3

f{x).

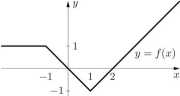
15. Na rysunku przedstawiono wykres funkcji y Narysować wykresy funkcji:

(b) y = f(x + 1); (d) y = f(-x); (f) y = /(3x);

(h)y = f(\x\).

(a) y = f(x) + 3;

(c) y =

(e) y =

(g) y = l/(®)l;

16. (P) Korzystając z wykresu funkcji y = sin x naszkicować wykresy funkcji:

(a) y = sin2x;	(b) y - sin|;	(c) y = sin ^ ;
(d) y = 1 + sin x;	(^e) y ^= ^ sina; — 1;	(f) 2/ = sin2^r- 0.
17. Naszkicować wykresy funkcji:
(a) y = |cosa:|; (b) y =	^sinz-pyH^; (c )y =	|tgx| ctg X.
18. Uzasadnić tożsamości trygonometryczne:
1 + tga (^a) ^-= tg a; ' 1 + ctg a	(b) sin^4 a+cos^4 a —	1 — i sin^2 2a; (c) tg a + ctg a =
,,, a 1 — cos a <^d>^t62 sin. ^;	(e) sin^4 a—cos^4 a = i	sin^2 a—cos^2 a; (f) —---cos a cos a

2

sin 2a ’

Dla jakich kątów a są one prawdziwe? 19. (P) Podaj wartości wyrażeń:

-73/2)

(d) arc tg 73 — arc ctg 73.

y/2    1    arc sin |

(a) arcsin— + arccos(b) arcctg 1 • arctg 1;    (c) -