70520498
51. Znaleźć wartości najmniejsze i największe podanych funkcji na wskazanych przedziałach:
(a) /(x) = 2x3 - 15x2 + 36x, [1,5]; (b) /(x) = *, [-4,2];
(c) f(x) = (x - 3)2e^, [-1,4]; (d) f(x) = 1 - |9 - x2|, [-5,1]; (f) f(x) = 2sinx + sin2x,
52. (P) Obliczyć /', f" funkcji:
(a) f(x) = 4x7 — 5x3 + 2x;
(d) f(x) = arc tg x\
53. Określić przedziały wypukłości
(c )/W = f;
(e) f(z) = sin3 x + cos3 x; (f) /(*) = x3lnx.
oraz punkty przegięcia wykresu funkcji:
(c)/w = ?ri2;
(f) |i3-4In|i|;
(b) /(x) = xe *;
(e> n4=jij,
(h) /(*)=«■“«*;
(a) f(x) = x(x- l)(x-3);
(d) f(x) = ln (l + x2);
(g) f(x) = sin x + i sin 2x;
8
Lista 9_
54. Zbadać przebieg zmienności podanych funkcji i następnie sporządzić ich wykresy:
(a) f(x) = («- lf(x + 2); (b) f(x) = W /(*) = yfji
(d)/(a)=3-i-l; (e) S(x) = xy/T=*-, (t)/W =
(g) m = xe‘“-, {h*)/(g)=smx + sin3xi (i) /(*) = x!lnx.
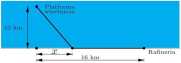
55. Platforma wiertnicza jest zakotwiczona na morzu 10 km od brzegu. Ropa z tej platformy będzie dostarczana rurociągiem do rafinerii położonej nad brzegiem morza, 16 km od punktu brzegu najbliższego platformie. Koszt ułożenia 1 km rurociągu na dnie morza wynosi 200 000 euro, a na lądzie -100 000 euro. Do którego miejsca na brzegu należy doprowadzić rurociąg, aby koszt jego budowy był najmniejszy?
56. Prostopadlościenny kontener ma mieć pojemność 22.50 m3 i kwadratową podłogę. Koszt lm2 blachy potrzebnej do wykonania jego podłogi i pokrywy wynosi 20 zł, a ścian bocznych - 30 zł. Jakie powinny być wymiary kontenera, aby koszt jego budowy był najmniejszy?
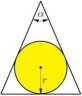
57. Jaka powinna być miara kąta a przy wierzchołku trójkąta równoramiennego o danym polu, aby promień koła r wpisanego w ten trójkąt był największy?
Wyszukiwarka