7543473348

/ -i

¥i

fi

\ >

♦ • j.

|Ł

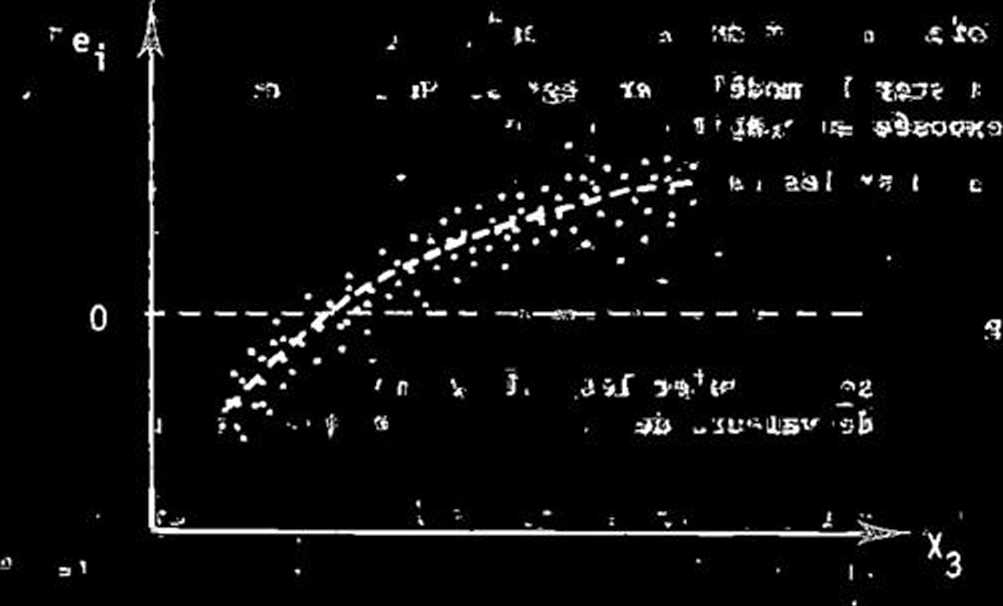
^{: 1}    La tendanoe moyenne (—---~) semble $tre 'une oourbe Ićą&rement

oonvexe₃ dont on peut probablement rendre oompte en ajoutant et (voir figurę A22 (e)) au motele ₃ ąui devient :

A

Y = b₀₊^b,^x, ♦ bĄ ♦ b₃X₃ ♦ b X| *’*    ***

Aprśs ajustement de oe seoond mod&le, le graphiąue des residus en fonction de X3 aura probablement une allure semblable au premier graphiąue prśsentś en (i) ci-dessus.

•I

A27 REGRESSION LINEAIRE PONDEREE

On utilise la regression linóaire ponderee (¹) ąuand les rósidus n’ont pas une variance homog&ne dans le domaine de uariation de Y . Ceei se produit frśąuemment ąuand on fait subir d la variable expliquee des trans-formations complexes ou ąuand on traite, dans des probldmes d'estimation de la production, des donnees de volume-(oii- la variance augmente avec le volume).    * i ■ . •

Dans la rigression linćaire ponderee, on assooie a chaąue obser-Wation i un poids judioieusement dóterminć ₃ soit empiriąuement, soit par des consitterations thćoriąues, et on minimise la sorme E e?    (mćthode

des moindres carrós pondćrćs (²)). C^rest en prenant pour de3 valeurs

proportionnelles a 1/s?    ₃ ou est?l^fścgrt-tyge'de Y •pour la valęur Y^ ,

ąu'on obtient le meilleur ajustement.

cti *

A'

(,^l) on anglais = weighted linear regression (²) en anglais = weighted least sguares

J.

i .