8960329740

Politechnika Opolska

Do jej opisu można użyć, analogicznie jak w przypadku pola magnetostatycznego, funkcji skalarnej d>, noszącej nazwę zredukowanego magnetycznego potencjału skalarnego, w postaci:

H_m = -grad®.    (2.12)

Korzystając z warunku bezźródłowości pola magnetycznego oraz zależności (2.8) otrzymuje się:

div(jjH_s) = div(jU grad®).    (2.13)

W modelowaniu zagadnień z magnesami trwałymi stosuje się zmodyfikowaną zależność materiałową opisaną wzorem:

(2.14)

Równanie (2.13) rozbudowuje się zatem o dodatkowy składnik i przyjmuje postać:

div(jjH_s) - div(juH_c) = div(ju grad®).    (2.15)

Największą wadą metody zredukowanego potencjału skalarnego jest mała dokładność obliczeń w obszarach zawierających materiały magnetyczne. Jest to podyktowane redukowaniem się wypadkowego natężenia pola magnetycznego, w związku z podobnymi wartościami wektorów H_s oraz H_m, mających przeciwne zwroty. Jednym z podejść umożliwiających wyeliminowanie tych niedogodności jest podział rozpatrywanego obszaru na podobszary: V® - o przenikalności //o ze źródłami pola oraz W - obejmujący pozostałą część zagadnienia. Używając do opisu odpowiednio zredukowanego oraz globalnego skalarnego potencjału magnetycznego. Jednoznaczne rozwiązanie zagadnienia wymaga jeszcze zastosowania odpowiednich warunków na granicach różnie opisanych podobszarów. Warunek ciągłości składowej normalnej wektora indukcji oraz składowej stycznej wektora natężenia pola magnetycznego na granicy tych podobszarów zapisano poniżej [53, 71]:

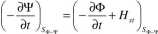
gdzie:

S<d-4' - powierzchnia graniczna pomiędzy podobszarami V® i VV;

H_s, - składowa styczna wektora H_s na powierzchni S®^.

Zastosowanie do obliczeń pary potencjałów A - V

Do opisu zagadnień elektrodynamiki technicznej często stosuje się również parę potencjałów: potencjał wektorowy pola magnetycznego A oraz potencjał skalamy pola elektrycznego V [35, 68]. Natężenie pola elektrycznego może być określone przez gradient funkcji skalarnej V. Związek pomiędzy natężeniem pola elektrycznego E oraz potencjałem V przedstawia równanie:

E = -grad V .    (2.17)

Pole magnetyczne jest polem wirowym, ze względu na ten fakt do jego opisu można użyć wektorowego potencjału pola magnetycznego zdefiniowanego poniżej:

18