9988995777

4 Próbny egzamin maturalny z matematyki. Poziom rozszerzony

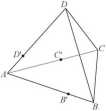
Zadanie 15. (0-4) Od czworościanu foremnego ABCD o krawędzi 4 odcięto płaszczyzną przechodzącą przez punkt B' na krawędzi AB, punkt C' na krawędzi AC i D’ na krawędzi AD ostrosłup AB’C'D', przy czym \AB'\ = 3, \AC'\ = 2, \AD'\ = 1.

a) Oblicz objętość ostrosłupa ABCD i AB'C'D'.

b) Oblicz wysokość ostrosłupa AB'C’D', gdy za jego podstawę przyjmiemy B'C'D'.

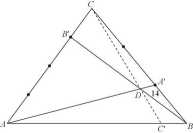
Zadanie 16. (0-4) W trójkącie ABC zaznaczono punkt A' na boku BC, tak że \A'B\: \A'C\ = 1 : 2, i punkt B' na boku AC, tak że \B'A\ : \B'C\ = 3:1. Odcinki AA' i BB' przecinają się w punkcie D. Prosta CD przecina odcinek AB w punkcie C.

Pole trójkąta BA'D jest równe 14.

a) Oblicz pole trójkąta ABC.

b) Oblicz stosunek \CD\:\DC'\.

Zadanie 17. (0-4) Pole powierzchni całkowitej stożka to n.

a) Jaka jest możliwie największa objętość takiego stożka?

b) Jakim trójkątem jest przekrój osiowy stożka o największej objętości?

Zadanie 18. (0-4) W grani astosłupie prostym prostokątnym ABCDEFGH krawędzie podstawy mają długość 3 i 4 (\AB\ = 4, \BC\ = 3), a wysokość 10. Dodatkowo wyróżnione są trzy punkty: punkt B' na krawędzi BF w odległości 3 od wierzchołka B, punkt C' na krawędzi CG w odległości 7 od wierzchołka C i punkt D' na krawędzi DH w odległości 4 od wierzchołka D.

a) Udowodnij, że płaszczyzna B'C'D' przecina krawędź AE w punkcie ,4.

b) Oblicz pole przekroju graniastosłupa ABCDEFGH płaszczyzną B'C'D'.

c) Oblicz cosinus kąta między płaszczyzną B'C'D' i płaszczyzną podstawy ABCD.

d) Oblicz objętość mniejszej części graniastosłupa powstałej z przecięcia płaszczyzną B'C'D'.

Zadanie 19. (0-4) a) Jeśli na trójkącie opiszemy okrąg, to z każdego łuku, na który podzieliły okrąg wierzchołki tego trójkąta, widać trójkąt pod pewnym kątem (zobacz na rysunku poniżej). Udowodnij, że a'+p' = y+ 180° f}' + y' = a+ 180° a' + y'=p+ 180°.

fr~l=ll Oficyna Edukacyjna * Krzysztof Pazdro