Sławomir Kulesza

[e-mail]

Cyfrowe przetwarzanie sygnałów (8)

Wykład dla studentów I roku (N)SMU WMiI

Specjalność: Techniki multimedialne

1 (39)

Wymierna z-transformata

W przypadku analizowanych układów LTI czasu dyskretnego, wszystkie

stosowane z-transformaty są funkcjami wymiernymi zmiennej z

-1

, czyli ułamkami

postaci:

H  z =

P  z 

D  z 

=

p

0



p

1

z

−

1



p

2

z

−

2



... p

M

z

−

M

d

0



d

1

z

−

1



d

2

z

−

2



...d

N

z

−

N

Lub równoważnie:

H  z=z

N −M

p

0

z

M



p

1

z

M −1



p

2

z

M −2



... p

M

d

0

z

N



d

1

z

N −1



d

2

z

N −2



...d

N

2 (39)

Zera i bieguny z-transformaty

Wymierna z-transformata może być również przedstawiona w postaci iloczynowej:

H  z =

p

0

d

0

⋅

∏

k =1

M



1−z

k

z

−

1



∏

k =1

N



1− p

k

z

−

1



=

G z

N −M

∏

k =1

M



z−z

k



∏

k =1

N



z− p

k



gdzie wartości {z

1

, z

2

, ..., z

M

} będące pierwiastkami licznika zwane są zerami

funkcji H(z) (zeros), zaś wartości {p

1

, p

2

, ..., p

N

} będące pierwiastkami mianownika

zwane są biegunami funkcji H(z) (poles).

Zauważmy, że:

H  z

k

=

0 ; H  p

j

=±∞

3 (39)

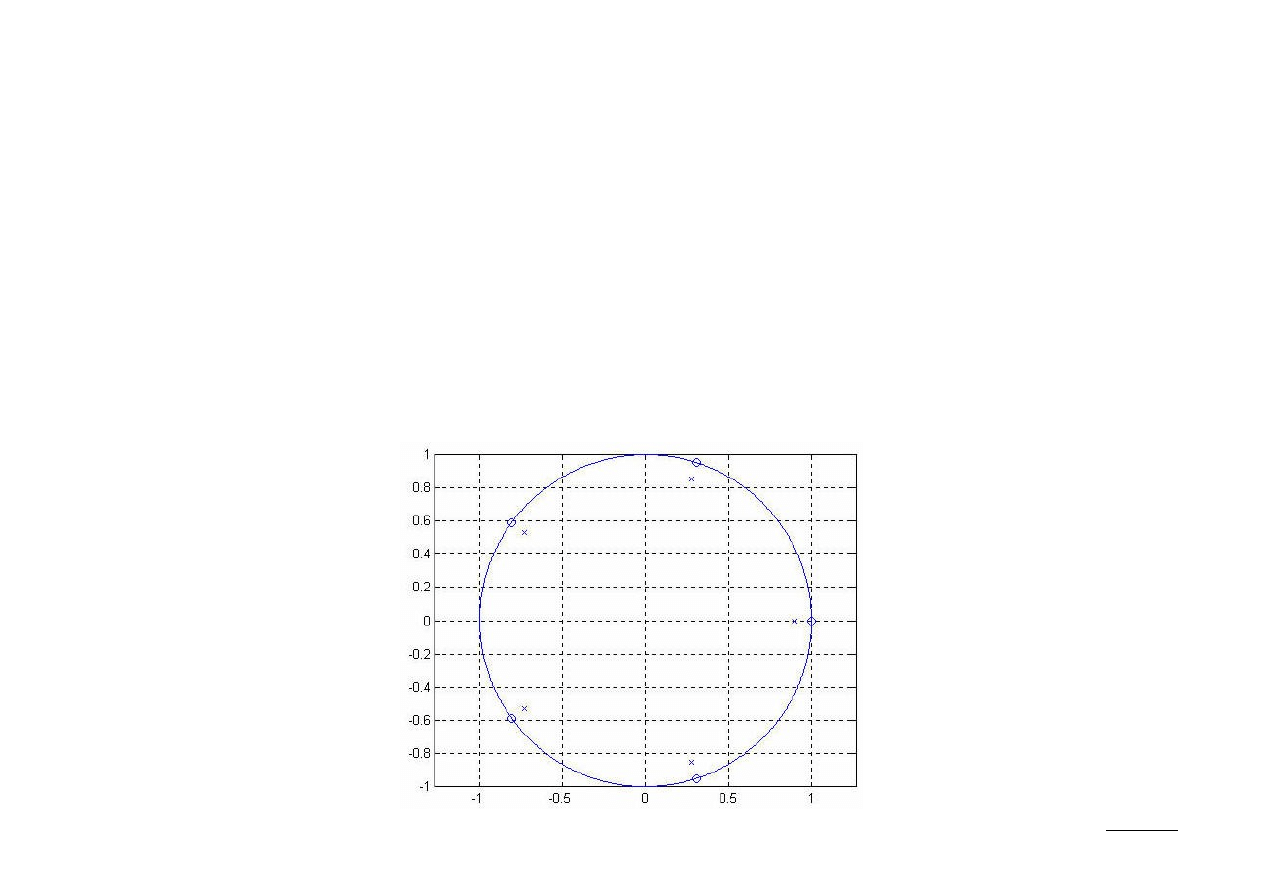
Wykres zer i biegunów

Graficzne przedstawienie funkcji H(z) na płaszczyźnie zespolonej nosi nazwę

wykresu zerowo-biegunowego (pole-zero plot), na którym bieguny zaznacza się

krzyżykami (x), zaś zera kółeczkami (o). Bieguny lub zera wielokrotne opisywane

są przez podanie odpowiedniej liczby w ich sąsiedztwie. Z definicji, wszystkie

bieguny i zera umiejscowione są poza obszarem zbieżności z-transformaty

(ROC).

4 (39)

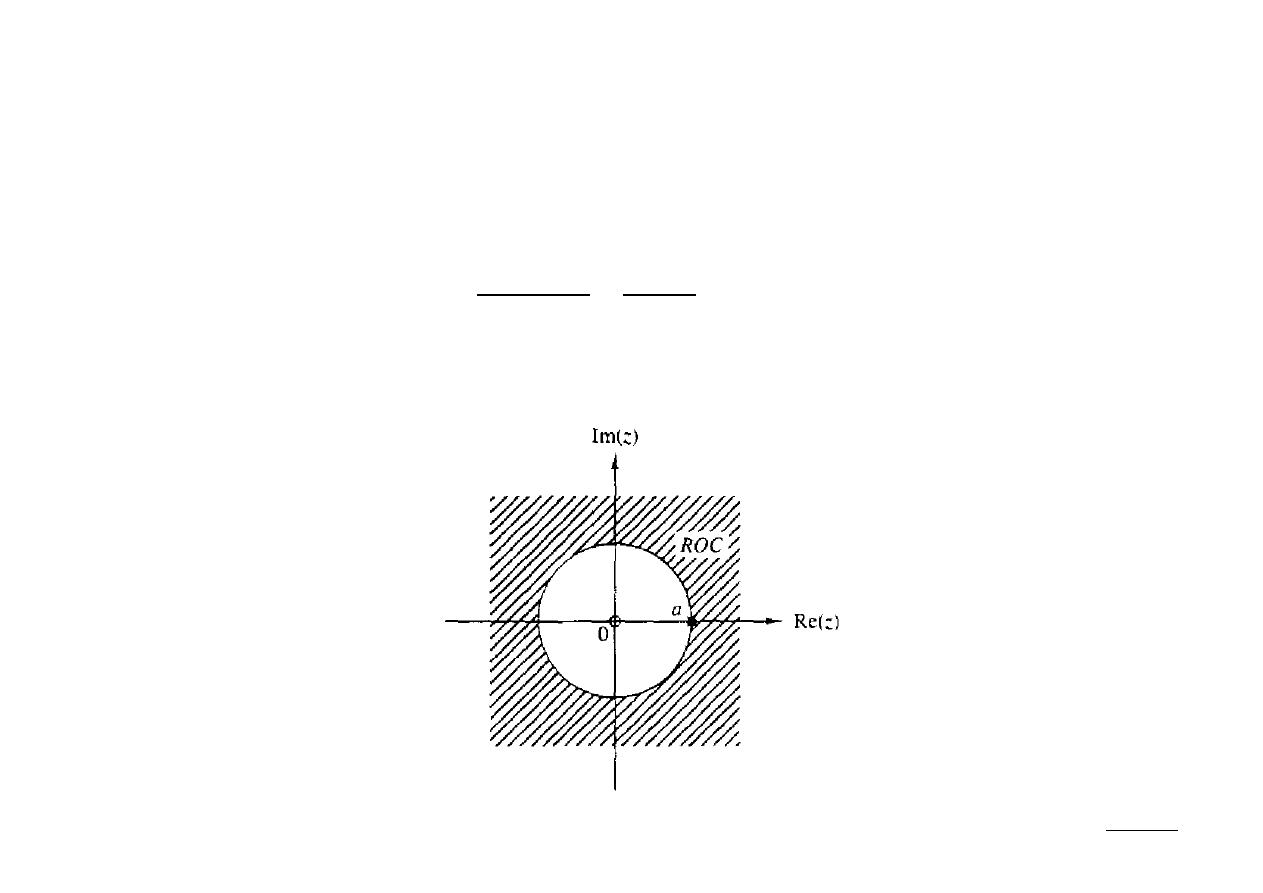
Ex.: Sporządzić wykres biegunów i zer dla sygnału:

x [n]=a

n

u[n] , a0

z-transformata sygnału x[n] ma postać:

X  z =

1

1−az

−

1

=

z

z−a

; ROC :∣z∣a

Wynika stąd, że z-transformata posiada 1 biegun (p

1

= a) oraz 1 zero (z

1

= 0).

5 (39)

Ex.: Sporządzić wykres biegunów i zer dla sygnału:

x [n]=a

n



u[n]−u[n−M ]



, a0

z-transformata sygnału x[n] ma postać:

X  z =

∑

n=0

M −1



az

−

1



n

=

1−az

−

1



M

1−az

−

1

=

z

M

−

a

M

z

M −1



z−a

Ponieważ a > 0, więc mianownik z-transformaty posiada w ogólności

M-pierwiastków:

z

k

=

a e

i 2 k

M

; k=0,1, 2,... , M −1

Okazuje się jednak, że zero dla z

0

= a kasuje biegun dla p

0

= a, skąd

otrzymujemy:

X  z=



z−z

1



z−z

2



... z−z

M −1



z

M −1

6 (39)

X  z =



z−z

1



z−z

2



... z−z

M −1



z

M −1

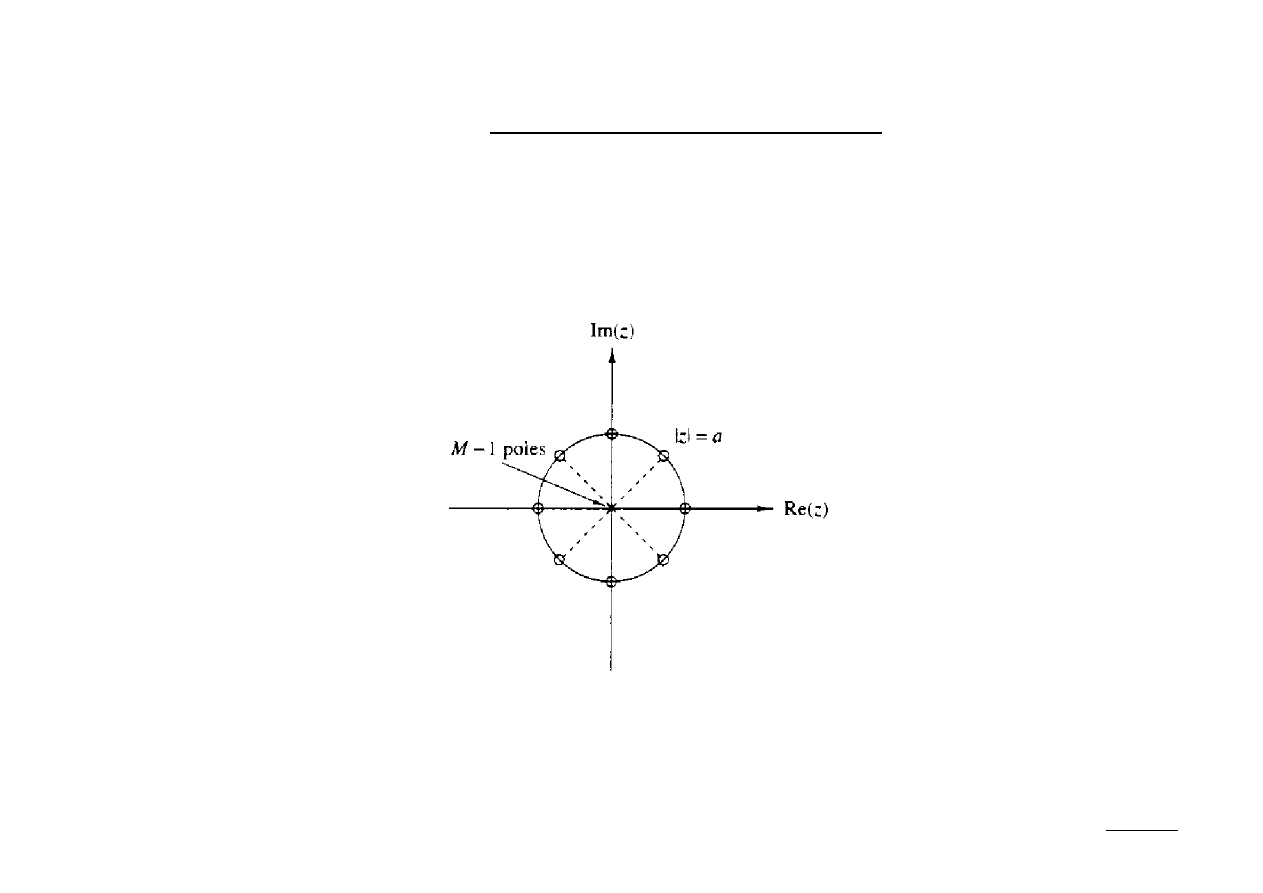
Powyższa funkcja posiada (M-1)-zer oraz biegunów ulokowanych jak na

poniższym rys. (M = 8):

Zauważmy, że ROC jest całą płaszczyzną zespoloną za wyjątkiem początku

układu, w którym ulokowano (M-1)-biegunów z-transformaty.

7 (39)

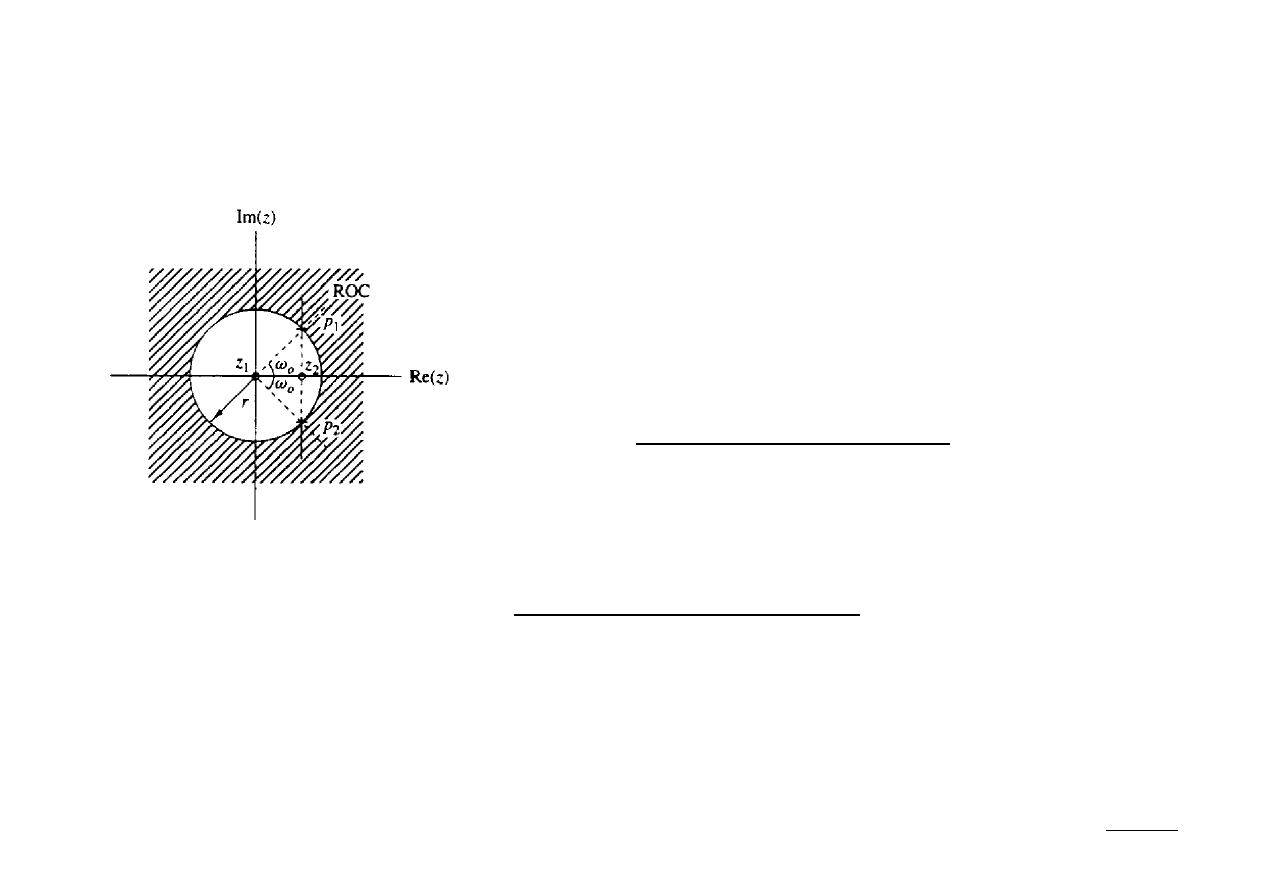
Ex.: Wyznaczyć z-transformatę oraz sygnał odpowiadający wykresowi zer

i biegunów jak na poniższym rysunku:

Układ ma dwa zera (M=2): z

1

= 0, z

2

= r cos ω

0

, oraz

dwa bieguny (N=2): p

1

= r e

iω0

, p

2

= r e

-i ω0

.

Po podstawieniu tych wartości, z-transformata

przyjmuje postać:

X  z =G

z⋅ z−r cos 

0





z−r e

i 

0



z−r e

−

i 

0



; ROC :∣z∣r

Po uporządkowaniu:

X  z =

1−r z

−

1

cos

0

1−2 r z

−

1

cos 

0



r

2

z

−

2

Skąd po porównaniu z tablicami par z-transformat otrzymujemy, że:

x [n]=G r

n

cos

0

nu[ n]

8 (39)

Położenie biegunów a charakterystyka czasowa sygnałów

przyczynowych

Przeanalizujmy zależności pomiędzy położeniem biegunów na płaszczyźnie

zmiennej zespolonej z a kształtem sygnału w dziedzinie czasu, ograniczając się

do rzeczywistych sygnałów przyczynowych.

Okazuje się, iż charakterystyczne zachowanie sygnałów przyczynowych zależy od

położenia biegunów względem koła jednostkowego (koła o promieniu |z| = 1).

Z ostatniego przykładu wynika przy tym, iż aby wielomian posiadał współczynniki

rzeczywiste, jego pierwiastki muszą być albo liczbami rzeczywistymi, bądź też

muszą występować jako pary sprzężone i dlatego analizie poddane zostaną

następujące przypadki: 1 biegun pojedynczy, 1 biegun podwójny, para biegunów

sprzężonych.

9 (39)

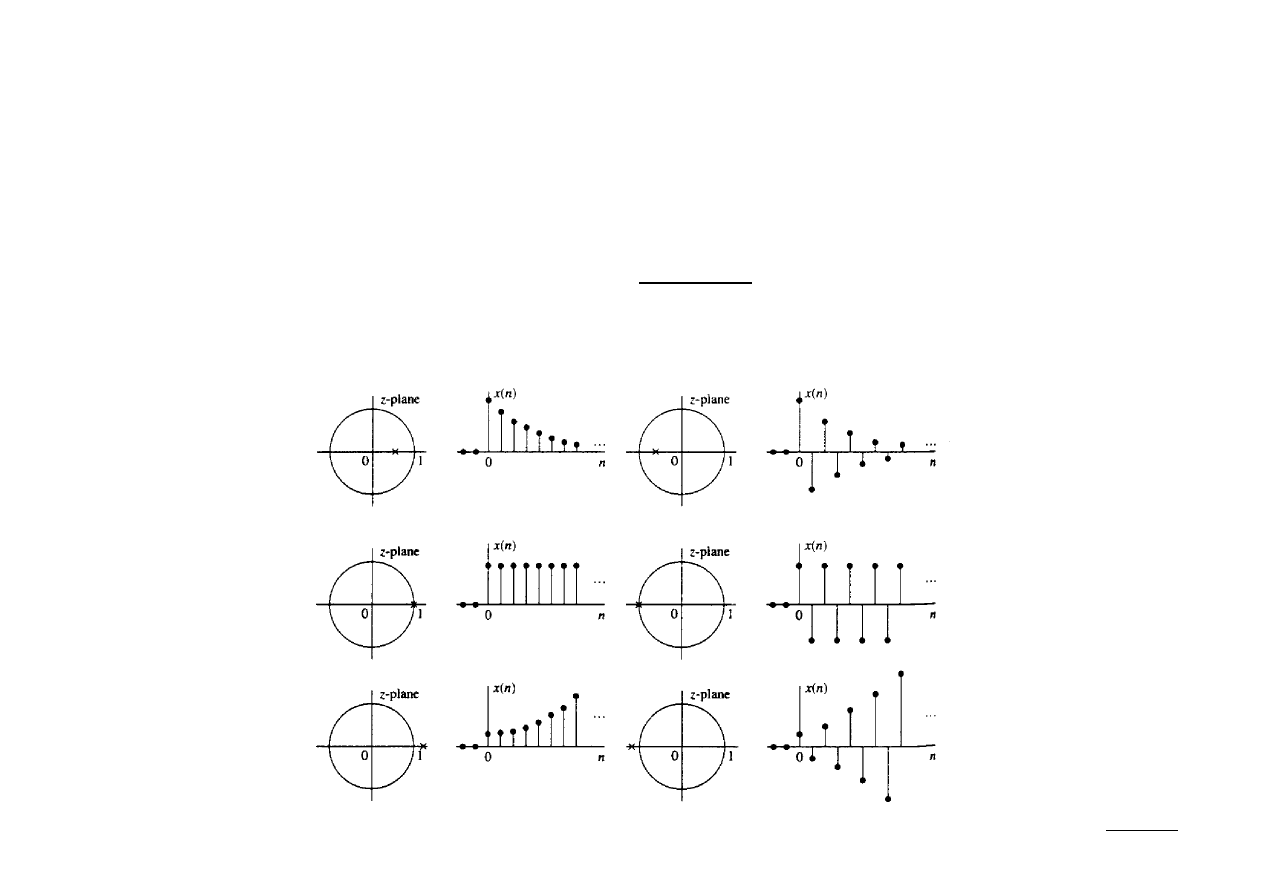
(1) Sygnał rzeczywisty z z-transformatą o 1 biegunie:

W takim przypadku biegun musi być liczbą rzeczywistą (leży na osi Re(z) – brak

pary sprzężonej). Jedynym sygnałem spełniającym taki warunek jest para:

x [n]=a

n

u[n]⇔ X  z=

1

1−az

−

1

; ROC :∣z∣∣a∣

Posiada ona zero dla z

1

= 0 oraz biegun dla p

1

= a.

10 (39)

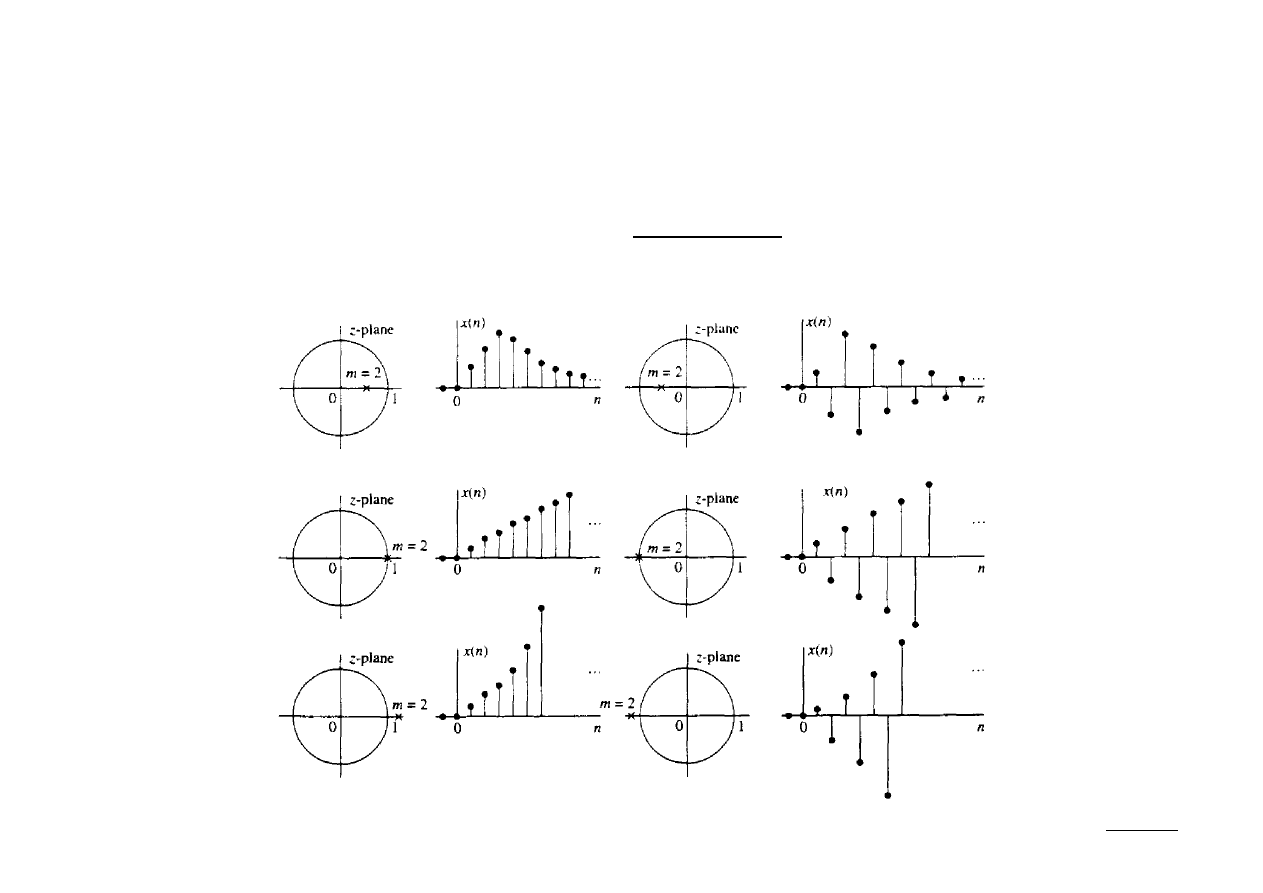
(2) Sygnał z z-transformatą o podwójnym biegunie rzeczywistym:

Przyczynowy sygnał rzeczywisty tego typu ma postać:

x [n]=n a

n

u[ n]⇔ X  z =

az

−

1



1−az

−

1



2

; ROC :∣z∣∣a∣

11 (39)

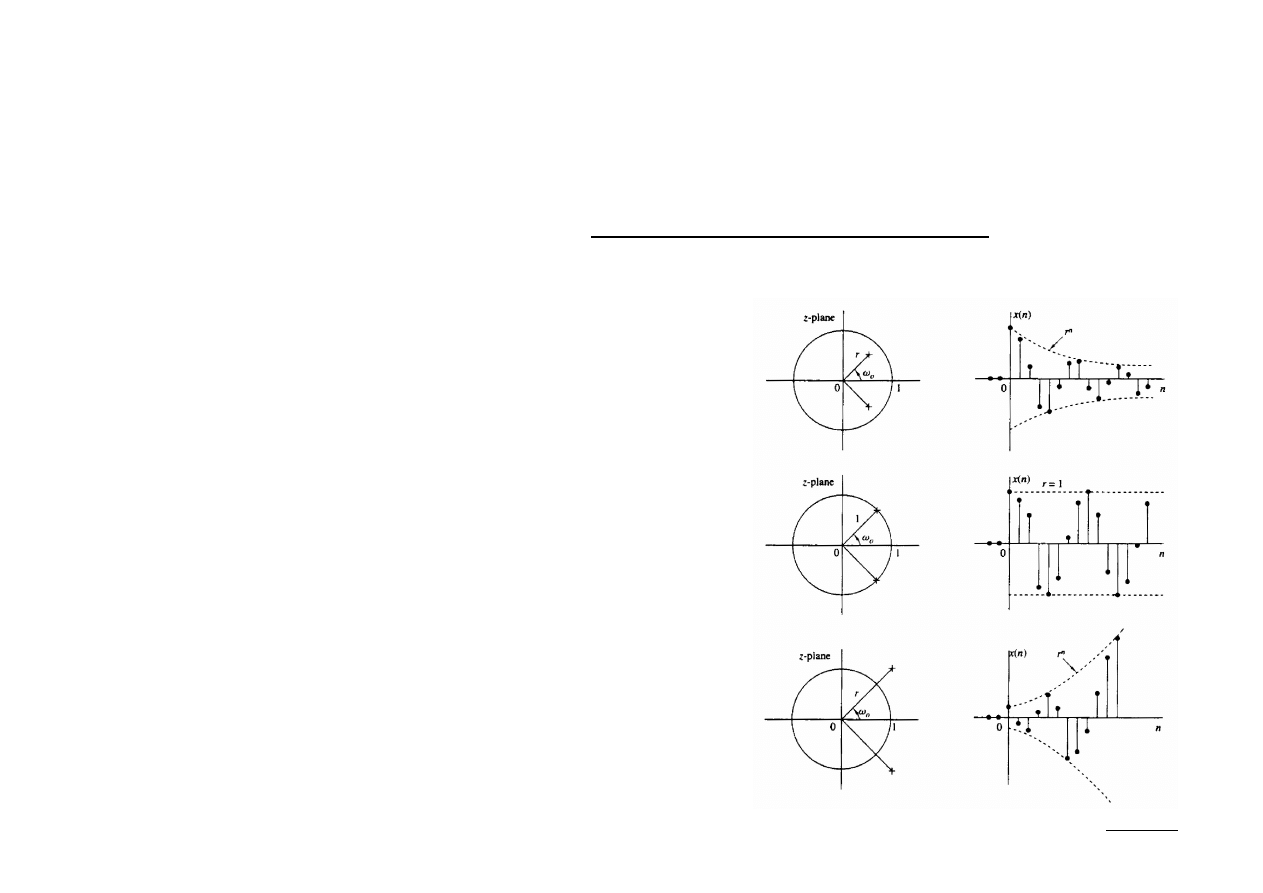
(3) Sygnał rzeczywisty z z-transformatą o parze biegunów sprzężonych:

Przyczynowy sygnał rzeczywisty ma postać:

x [n]=a

n

cos

0

nu[ n]⇔ X  z =

1−az

−

1

1−2 a z

−

1

cos

0

na

2

z

−

2

; ROC :∣z∣∣a∣

Odległość biegunów od początku układu określa

obwiednię sygnału, zaś kąt do osi Re(z) – jego

częstotliwość.

12 (39)

Położenia biegunów sygnałów przyczynowych – wnioski

–

Bieguny modyfikują zachowanie sygnału znacznie silniej niż zera.

–

Rzeczywiste sygnały przyczynowe o pojedynczych biegunach rzeczywistych lub

pojedynczych parach biegunów sprzężonych położonych wewnątrz koła

jednostkowego lub na jego obwodzie, są zawsze ograniczone w amplitudzie.

–

Bieguny położone bliżej początku układu współrzędnych powodują szybszy

zanik sygnału niż bieguny położone przy obwodzie koła jednostkowego

(ale w jego wnętrzu).

–

Układy LTI o odpowiedzi impulsowej (sygnał przyczynowy) z biegunami

leżącymi poza kołem jednostkowym są niestabilne – ich odpowiedź impulsowa

nie jest bezwzględnie sumowalna.

13 (39)

Funkcja przenoszenia układów LTI

Wiemy już, że odpowiedź układu LTI na pobudzenie x[n] można otrzymać licząc

splot tego sygnału z odpowiedzią impulsową układu h[n]. W dziedzinie

z-transformaty związek ten wyraża się prostym iloczynem:

Y  z =H  z ⋅X  z 

gdzie Y(z) jest z-transformatą odpowiedzi y[n], H(z) – z-transformatą odpowiedzi

impulsowej h[n], zaś X(z) – z-transformatą pobudzenia x[n].

Jak widać, h[n] charakteryzuje układ w dziedzinie czasu, zaś H(z) –

charakteryzuje ten sam układ w dziedzinie z-transformaty. Funkcję H(z) nazywa

się funkcją przenoszenia (system function, transfer function).

14 (39)

Wyrażenie funkcji przenoszenia w postaci funkcji wymiernej:

H  z =

Y  z 
X  z 

jest szczególnie wygodne w przypadku układów LTI opisywanych równaniami

różnicowymi o stałych współczynnikach:

y [n]=−

∑

k=1

N

a

k

y [n−k ]

∑

k=0

M

b

k

x [n−k ]

Funkcję przenoszenia H(z) można wówczas wyznaczyć wprost jako

z-transformatę y[n] postaci:

Y  z =−

∑

k =1

N

a

k

Y  z  z

−

k



∑

k=0

M

b

k

X  z  z

−

k

15 (39)

Po przekształceniach otrzymujemy:

Y  z



1

∑

k =1

N

a

k

z

−

k



=

X  z 

∑

k =0

M

b

k

z

−

k

H  z =

Y  z 
X  z 

=

∑

k =0

M

b

k

z

−

k

1

∑

k =1

N

a

k

z

−

k

Tak więc układy LTI opisywane równaniami różnicowymi o stałych

współczynnikach posiadają wymierne funkcje przenoszenia.

16 (39)

Powyższa ogólna postać funkcji przenoszenia ma 2 przypadki szczególne:

(1) a

k

= 0 dla wszystkich 1 ≤ k ≤ N:

H  z =

∑

k =0

M

b

k

z

−

k

=

z

−

M

∑

k =0

M

b

k

z

M −k

H(z) zawiera M-zer zależnych od b

k

oraz M-krotny biegun w początku układu

(p = 0). Układ taki nazywa się układem zerowym (all-zero system). Odpowiedź

impulsowa takiego układu jest skończona – jest to układ FIR.

(2) b

k

= 0 dla wszystkich 1 ≤ k ≤ M:

H  z =

b

0

1

∑

k =1

N

a

k

z

−

k

=

b

0

z

N

∑

k =0

N

a

k

z

N −k

Jest to układ biegunowy (all-pole system), gdzie bieguny uwarunkowane są

wartościami a

k

. Odpowiedź impulsowa jest nieskończona, a więc jest to układ IIR.

17 (39)

Ex.: Wyznaczyć funkcję przenoszenia oraz odpowiedź impulsową układu

opisywanego równaniem różnicowym:

y [n]=

1

2

y [n−1]2 x [n]

z-transformata równania różnicowego ma postać:

Y  z=

1
2

z

−

1

Y  z 2 X  z 

Funkcja przenoszenia przyjmuje więc postać:

H  z =

2

1−1/2 z

−

1

Układ posiada biegun dla z = 0.5 oraz zero dla z = 0. Korzystając z tabel

z-transformat znajdziemy, że jego odpowiedź impulsowa wynosi:

h[n]=2



1

2



n

u[n]

18 (39)

Obliczanie odwrotnej z-transformaty

Formalna definicja odwrotnej z-transformaty ma postać:

x [n]=

1

2 i

∮

C

X  z  z

n−1

dz

Jest to całka krzywoliniowa po zamkniętym konturze C, który jest całkowicie

zawarty w ROC funkcji X(z) oraz zawiera początek płaszczyzny zespolonej.

W najprostszym przypadku C może być okręgiem o środku w początku

płaszczyzny zespolonej, zawartym w ROC.

Zasadniczo istnieją 3 metody znajdowania odwrotnej z-transformaty:

–

obliczanie całki krzywoliniowej,

–

rozwinięcie X(z) na szereg potęgowy zmiennej z

k

oraz z

-k

,

–

rozwinięcie na ułamki właściwe i odczytanie rozwiązania z tablicy.

19 (39)

Obliczanie odwrotnej z-transformaty przez rozwinięcie w szereg

potęgowy zmiennej z

Mając daną z-transformatę X(z) wraz z jej obszarem zbieżności, rozwijamy ją

w szereg potęgowy postaci:

X  z =

∑

n=−∞

∞

c

n

z

−

n

Powyższy szereg musi być zbieżny w danym ROC.

Jednoznaczność z-transformaty gwarantuje wówczas, że:

∀

n∈ℤ

x [n]=c

n

20 (39)

Ex.: Wyznaczyć odwrotną z-transformatę funkcji:

X  z =

1

1−1.5z

−

1



0.5z

−

2

dla (a) ROC: |z| > 1, (b) |z| < 0.5.

(a) Ponieważ ROC leży na zewnątrz koła, x[n] musi być sygnałem przyczynowym.

Poszukiwany szereg potęgowy będzie więc zawierał wyłącznie wyrazy typu z

-k

,

a jego ostateczną postać znajdziemy poprzez długie dzielenie wielomianów:

21 (39)

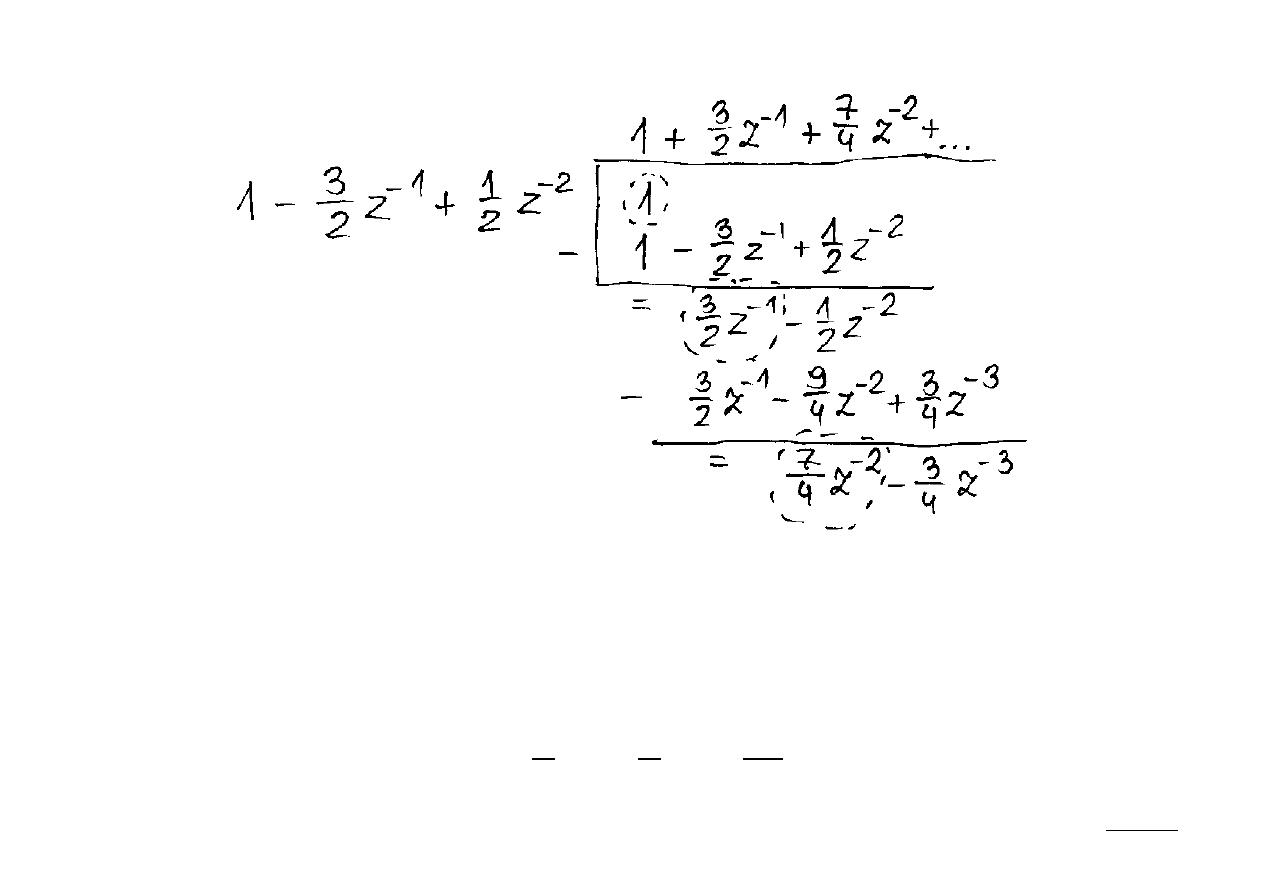
Ostatecznie obliczamy, że:

X  z =1

3
2

z

−

1



7
4

z

−

2



15

8

z

−

3



...

22 (39)

Stąd mamy, że:

x [n]=[1 ,

3
2

,

7
4

,

15

8

,...]

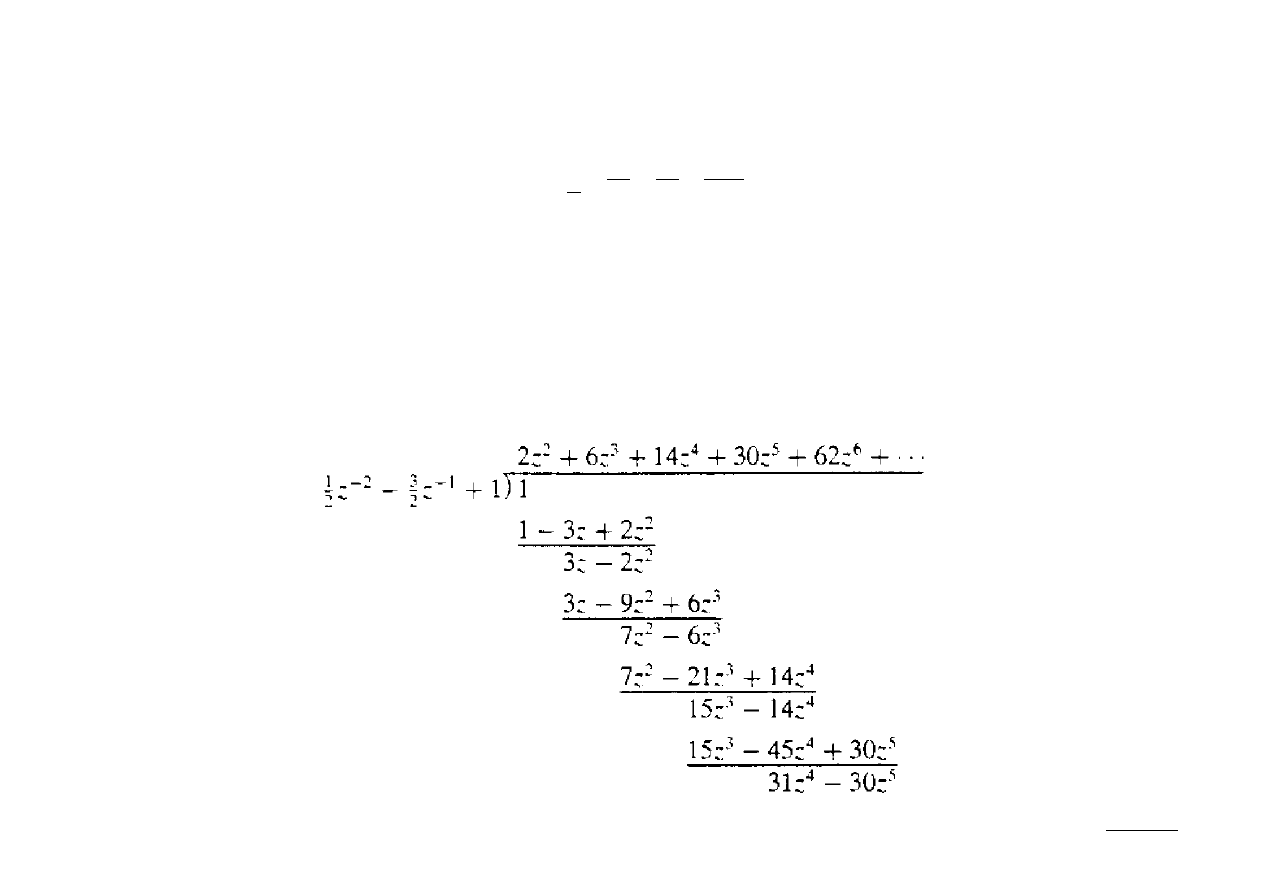
(b) W tym przypadku ROC znajduje się we wnętrzu koła, tak więc x[n] musi być

antyprzyczynowy, zaś współczynniki rozwinięcia muszą być potęgami dodatnimi.

Dzielenie wygląda tu następująco:

23 (39)

Skąd otrzymujemy, że:

X  z =2 z

2



6 z

3



14 z

4



30 z

5



62 z

6



...

Ostateczny wynik ma więc postać:

x [n]=[... 62,30, 14,6, 2, 0,0]

Z powyższych przykładów wypływa wniosek, iż metoda długiego dzielenia staje

się uciążliwa w przypadku długich ciągów, gdyż prowadzi ona do uzyskania

konkretnych wartości kolejnych próbek odwrotnej z-transformaty, a nie do

wyznaczenia jej postaci analitycznej.

24 (39)

Odwracanie z-transformaty przez upraszczanie funkcji

wymiernych

Metoda tablicowa jest skuteczna, gdy szukaną odwrotną z-transformatę uda się

zapisać w postaci kombinacji liniowej z-transformat stablicowanych. Jest to

narzędzie szczególnie wydajne w przypadku X(z) będących funkcjami wymiernymi

postaci:

X  z =

N  z

D  z 

=

b

0



b

1

z

−

1



...b

M

z

−

M

1a

1

z

−

1



...a

N

z

−

N

;a

0

=

1

Powyższa funkcja wymierna jest funkcją właściwą, gdy a

0

≠ 0 oraz M < N, a więc

gdy liczba ograniczonych (w sensie amplitudy) zer jest mniejsza niż liczba

ograniczonych biegunów.

Każdą funkcję niewłaściwą (M ≥ N) zawsze można przedstawić jako sumę

wielomianu i funkcji wymiernej właściwej.

25 (39)

Rozdzielone bieguny

Zakładając, że wszystkie bieguny funkcji X(z) p

1

, p

2

, .., p

N

są rozdzielone,

szukamy rozwinięcia funkcji wymiernej w postaci:

X  z

z

=

A

1

z− p

1



A

2

z− p

2



...

A

N

z− p

N

Kolejnym zadaniem jest wyznaczenie wartości współczynników A

1

, ..., A

N

.

Ex.: Rozłożyć powyższą metodą funkcję wymierną X(z) = (1-1.5z

-1

+0.5z

-2

)

-1

.

26 (39)

Analiza układów LTI w domenie z-transformaty

Odpowiedź układu LTI o wymiernej funkcji przenoszenia:

Rozważmy układ zerowo-biegunowy opisywany równaniem różnicowym postaci:

y [n]=−

∑

k=1

N

a

k

y [n−k ]

∑

k=0

M

b

k

x [n−k ]

którego funkcja przenoszenia opisywana jest wzorem:

H  z =

Y  z 
X  z 

=

∑

k =0

M

b

k

z

−

k

1

∑

k =1

N

a

k

z

−

k

=

B  z 

A z 

Załóżmy dodatkowo, że z-transformata pobudzenia x[n] również ma postać

wymierną:

X(z) = N(z)/Q(z)

27 (39)

Jeśli układ jest zrelaksowany, tzn.: y[-1] = y[-2] = ... = y[-N] = 0, wówczas

z-transformata odpowiedzi układu ma postać:

Y  z =H  z ⋅X  z =

B  z ⋅N  z

A z ⋅Q  z

Załóżmy teraz, że układ posiada rozdzielone bieguny p

1

, p

2

, ..., p

N

, zaś bieguny

z-transformaty pobudzenia to q

1

, q

2

, ..., q

L

, przy czym żadne dwa bieguny nie

pokrywają się ani ze sobą, ani z zerami wielomianów B(z) i N(z). Y(z) można

wówczas przedstawić w postaci:

Y  z=

∑

k =1

N

A

k

1− p

k

z

−

1



∑

k=1

L

Q

k

1−q

k

z

−

1

28 (39)

Odwrotna z-transformata odpowiedzi układu ma wówczas postać:

y [n]=

∑

k =1

N

A

k



p

k



n

u[n]

∑

k =1

L

Q

k



q

k



n

u[n]

Widać, że całkowita odpowiedź układu zawiera dwa składniki:

(1) pierwszy jest funkcją położenia biegunów układu {p

k

} i określany jest mianem

odpowiedzi naturalnej układu (natural response). Wpływ pobudzenia na

odpowiedź swobodną wyraża się jedynie w przeskalowaniu wartości

współczynników {A

k

}.

(2) drugi jest funkcją biegunów pobudzenia {q

k

} i określany jest mianem

odpowiedzi wymuszonej układu (forced response). Wpływ układu na

odpowiedź wymuszoną przejawia się w możliwym przeskalowaniu

współczynników {Q

k

}.

Uwaga! Odpowiedź naturalna i zerowa (ZIR) są różne!

29 (39)

Odpowiedź układu zero-biegunowego o niezerowych

warunkach początkowych

Załóżmy, że pobudzenie x[n] dostarczono do układu zerowo-biegunowego

w chwili n = 0, a więc jest to pobudzenie przyczynowe. Historia układu

(wpływ wcześniejszych sygnałów wejściowych) zawarta jest w warunkach

początkowych y[-1], y[-2], ..., y[-N]. Równanie różnicowe opisujące dany układ

włączając w to warunki początkowe ma postać:

∑

k=0

N

a

k



y [n−k ]

∑

j=1

k

y [− j]



=

∑

k =0

M

b

k

x [n−k ]

Skąd mamy, że w dziedzinie z-transformaty:

∑

k=0

N

a

k

z

−

k



Y  z 

∑

j=1

k

y [− j ] z

j



=

∑

k =0

M

b

k

z

−

k

X  z 

30 (39)

Po przekształceniach dostajemy, że:

Y  z =−

∑

k =1

N

a

k

z

−

k



Y  z 

∑

j=1

k

y [− j ] z

j





∑

k =0

M

b

k

z

−

k

X  z

gdzie domyślnie założono, że a

0

= 1.

Powyższą z-transformatę odpowiedzi można przedstawić w postaci:

Y  z =

∑

k =0

M

b

k

z

−

k

1

∑

k =1

N

a

k

z

−

k

X  z −

∑

k=1

N

a

k

z

−

k

∑

j=1

k

y [− j ] z

j

1

∑

k =1

N

a

k

z

−

k

Skąd mamy, że:

Y  z =H  z  X  z

N



z

A z 

31 (39)

Przy czym wzorze tym występuje wyrażenie:

N

0



z =−

∑

k =1

N

a

k

z

−

k

∑

j=1

k

y [− j ] z

j

Otrzymana z-transformata odpowiedzi całkowitej układu z niezerowymi

warunkami początkowymi składa się z 2 części:

(1) odpowiedź wymuszona, która w dziedzinie z-transformaty ma postać:

Y

zs

(z) = H(z)X(z),

(2) odpowiedź swobodna wynikająca z niezerowych warunków początkowych przy

braku pobudzenia: Y

zi

(z) = N

0

(z)/A(z).

32 (39)

Powyższe wyrażenie ma swój odpowiednik w dziedzinie czasu:

y[n] = y

zs

[n] + y

zi

[n]

Bieguny odpowiedzi swobodnej i naturalnej są identyczne, a więc niezerowe

warunki początkowe wpływają na wartości {A

k

}, ale nie mają za to wpływu na

odpowiedź wymuszoną układu:

y

zi

[

n]=

∑

k =1

N

D

k



p

k



n

u[n]

y [n]=

∑

k =1

N



A

k



D

k



p

k



n

u[n]

∑

k =1

L

Q

k



q

k



n

u[n]

33 (39)

Ex.: Wyznaczyć odpowiedź skokową (wymuszoną) układu:

y [n]=0.9 y [n−1]−0.81 y [n−2]x [n]

dla warunku początkowego: y[-1] = y[-2] = 1.

Funkcja przenoszenia ma postać:

H  z =

1

1−0.9 z

−

1



0.81z

−

2

W układzie występują dwa bieguny sprzężone:

p

1

=

0.9 e

i 

3

, p

2

=

0.9 e

−

i 

3

z-transformata skoku jednostkowego ma postać:

X  z =

1

1− z

−

1

34 (39)

Stąd odpowiedź wymuszona ma postać:

Y

zs



z =

1



1−0.9 e

i 

3

z

−

1



1−0.9 e

−

i 

3

z

−

1



1−z

−

1



=

...

...=

0.542−i 0.049

1−0.9 e

i 

3

z

−

1



0.542i 0.049

1−0.9 e

−

i 
3

z

−

1



1.099

1−z

−

1

Stąd ogólna postać odpowiedzi wymuszonej (dla zerowych warunków

początkowych) to:

y

zs

[

n]=[1.0991.0880.9

n

cos



3

n−5.2

0

]

u[n]

35 (39)

Dla zadanych niezerowych warunków początkowych dodatkowym wyrażeniem

w odpowiedzi wymuszonej jest:

Y

zi



z=

N

0



z 

A



z=

0.09−0.81 z

−

1

1−0.9 z

−

1



0.81 z

−

2

Stąd odpowiedź swobodna wynosi:

y

zi

[

n]=0.9880.9

n

cos



3

n87

0



u[n]

Całkowita odpowiedź układu dla zadanych warunków początkowych ma zatem

postać:

y [n]=1.099 u[n]1.440.9

n

cos



3

n38

0



u[n]

36 (39)

Odpowiedź przejściowa i stacjonarna

Naturalna odpowiedź układu LTI ma postać:

y

nat

[

n]=

∑

k =1

N

A

k



p

k



n

u[n]

Jeśli wszystkie bieguny tej odpowiedzi |{p

k

}| < 1, wówczas amplituda tej

odpowiedzi będzie z czasem zbiegać do zera. Taką odpowiedź naturalną

nazywamy odpowiedzią niestacjonarną (przejściową – transient response).

Odpowiedź wymuszona dana jest z kolei w postaci:

y

for

[

n]=

∑

k =1

L

Q

k



q

k



n

u [n]

Jeśli wszystkie bieguny |{q

k

}| < 1, wymuszenie jest niestacjonarne i zbiega do

zera, jednak jeśli |{q

k

}| = 1, to bieguny leżą na kole jednostkowym i wymuszenie

jest sinusoidalne, a y

for

[n] jest odpowiedzią stacjonarną (steady-state response).

37 (39)

Przyczynowość i stabilność układów LTI

w domenie z-transformaty

Układ LTI nazywamy przyczynowym, gdy:

∀

n0

h[n]=0

Z drugiej strony, jeśli układ jest przyczynowy, to jego ROC leży poza kołem

o promieniu r. Z tego względu układ LTI jest przyczynowy wtedy i tylko wtedy, gdy

ROC jego funkcji przenoszenia leży poza kołem o promieniu r < ∞.

Układ LTI jest stabilny wtedy i tylko wtedy gdy:

∑

n=−∞

∞

∣

h[n]∣∞

W dziedzinie z-transformaty warunek ten określa wymaganie, aby ROC funkcji

przenoszenia zawierało koło jednostkowe.

38 (39)

Znoszenie się biegunów i zer

Kiedy z-transformata posiada identyczne zera i bieguny, ulegają one skróceniu,

a więc nie pojawiają się w końcowym wyrażeniu na odwrotną z-transformatę.

Efekt ten może wystąpić zarówno dla funkcji przenoszenia H(z), jak i po jej

wymnożeniu z z-transformatą pobudzenia. W pierwszym przypadku mówimy

o redukcji rzędu funkcji przenoszenia, w drugim – wzajemnym wygaszaniu

biegunów (zer) funkcji przenoszenia przez zera (bieguny) pobudzenia.

39 (39)