Sławomir Kulesza

[e-mail]

Cyfrowe przetwarzanie sygnałów (4)

Wykład dla studentów I roku (N)SMU WMiI

Specjalność: Techniki multimedialne

Układy czasu dyskretnego – filtry cyfrowe

Zadaniem układów czasu dyskretnego (Discrete-Time Systems – DTS) jest

przetworzenie danego ciągu wejściowego x[n] na odpowiedni ciąg wyjściowy y[n].

Układ realizujący taką operację (przekształcenie T) może być zarówno układem

sprzętowym, jak i algorytmem programowym:

y [n]≡T  x [n]

W praktyce DSP wszystkie sygnały są cyfrowe, więc operacje na nich również

dają sygnały cyfrowe. Układy realizujące operacje na sygnałach cyfrowych

nazywa się filtrami cyfrowymi.

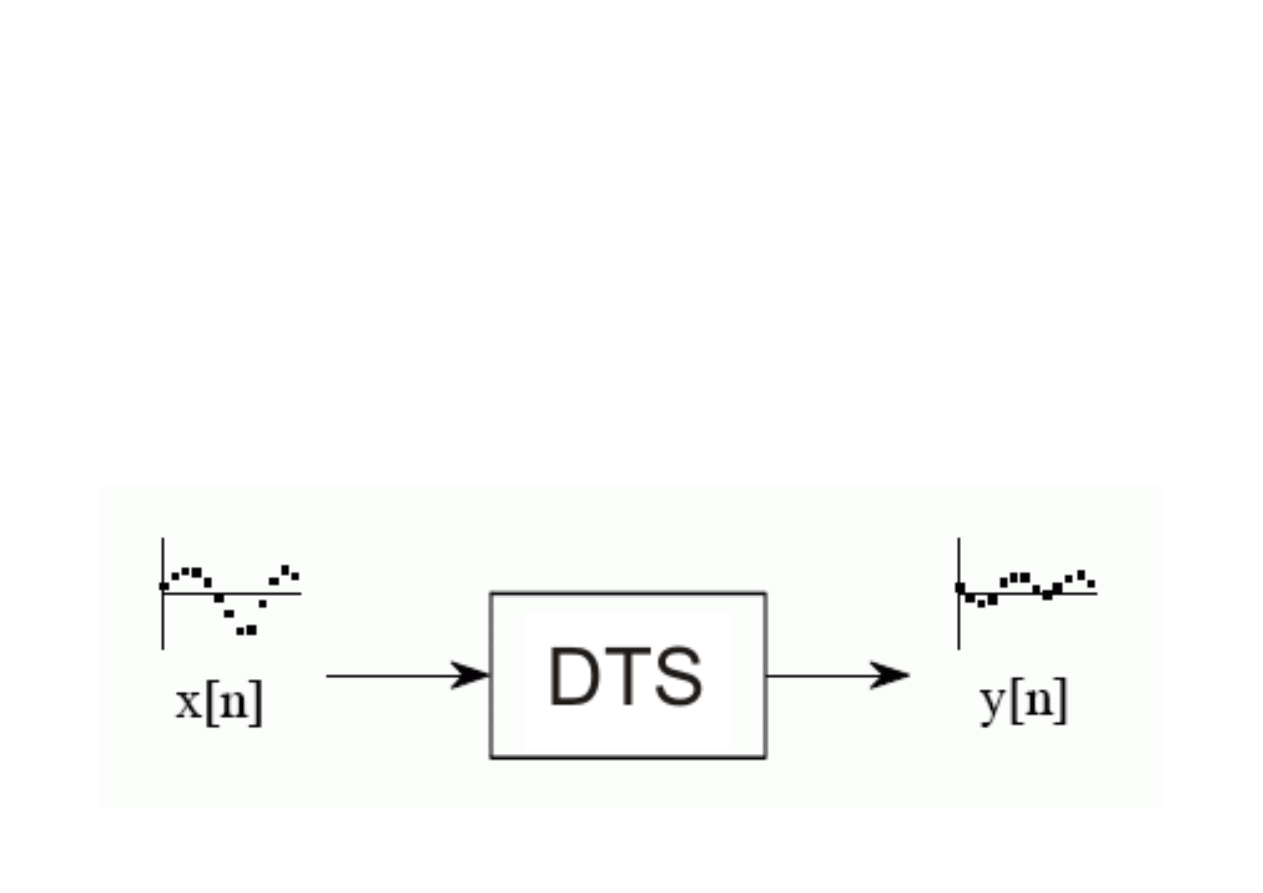
Charakterystyka wejściowo-wyjściowa DTS

Charakterystyka wejściowo-wyjściowa układów czasu dyskretnego zawiera jawną

matematyczną definicję zależności pomiędzy ciągiem wejściowym (pobudzeniem

układu) a wyjściowym (odpowiedzią układu). Pomija się przy tym całkowicie

wewnętrzną strukturę układu, co powoduje, że stanowi on dla użytkownika

'czarną skrzynkę'.

Przykłady charakterystyk I/O układów czasu dyskretnego

Znając pobudzenie x[n] postaci:

x [n]=

{

∣

n∣⇔∣n∣≤3
0⇔∣n∣3

}

Wyznacz odpowiedź następujących układów czasu dyskretnego:

–

y[n] = x[n] – układ tożsamościowy,

–

y[n] = x[n-1] – układ opóźniający,

–

y[n] = x[n+1] – układ przyspieszający,

–

y[n] = (x[n-1] + x[n] + x[n+1])/3 – układ uśredniający,

–

y[n] = max(x[n-1], x[n], x[n+1]) – dyskryminator (selektor),

–

y [n]=

∑

k =−∞

n

x [n]=x [n]x [n−1]x [n−2]... – akumulator.

Reprezentacja blokowa układów czasu dyskretnego

Diagram blokowy układu czasu dyskretnego zawiera elementarne bloki

funkcjonalne połączone siecią zależności odpowiednio do wykonywanej operacji.

Do bloków elementarnych zalicza się:

–

sumator,

–

wzmacniacz,

–

układ mnożący (modulator),

–

układ opóźniający,

–

układ przyspieszający,

–

rozdzielacz.

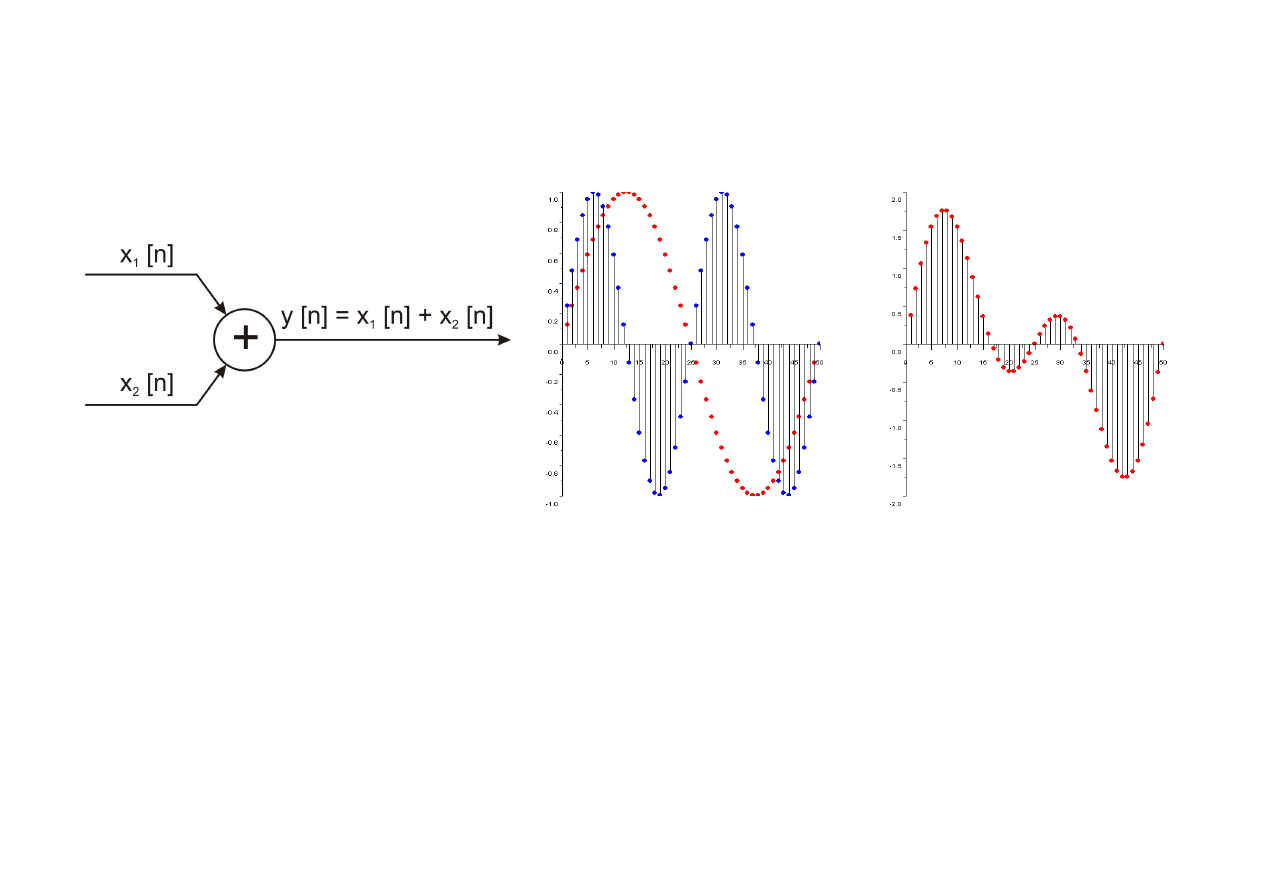
Sumator

Sumator realizuje operację dodawania dwóch ciągów:

y [n]= x

1

[

n]x

2

[

n]

Ponieważ do przeprowadzenia tej operacji wymagane są wyłącznie bieżące

próbki ciągów, układ jest bezpamięciowy.

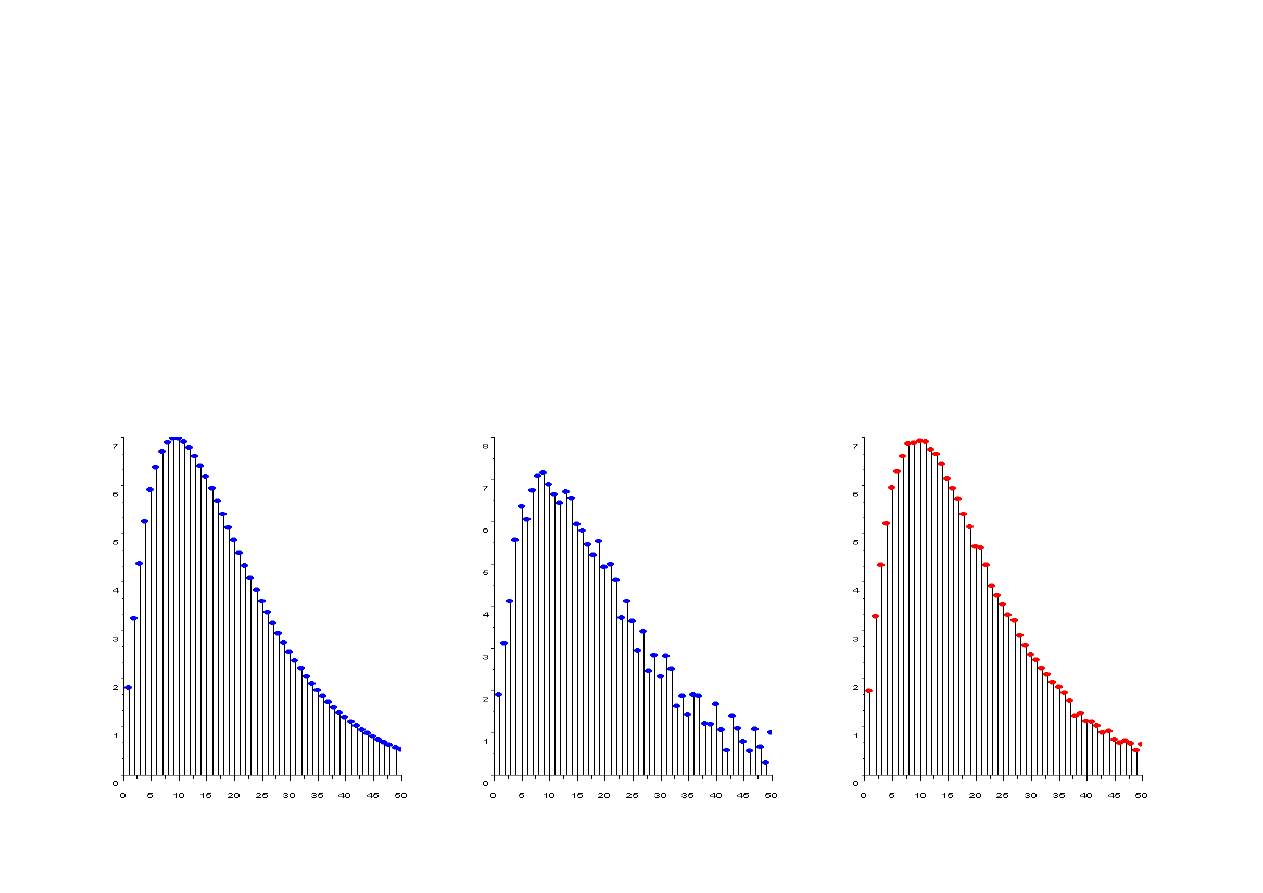
Zastosowania sumatora – odszumianie sygnału

Jednym z najprostszych zastosowań sumatora jest odszumianie sygnału metodą

wielokrotnego uśredniania. Wykorzystuje się przy tym fakt, iż przy wielokrotnych

pomiarach tego samego sygnału, sygnał użyteczny nie zmienia się w czasie,

podczas gdy sygnał szumu ulega losowym fluktuacjom i jego średnia wartość

w długim czasie wynosi 0.

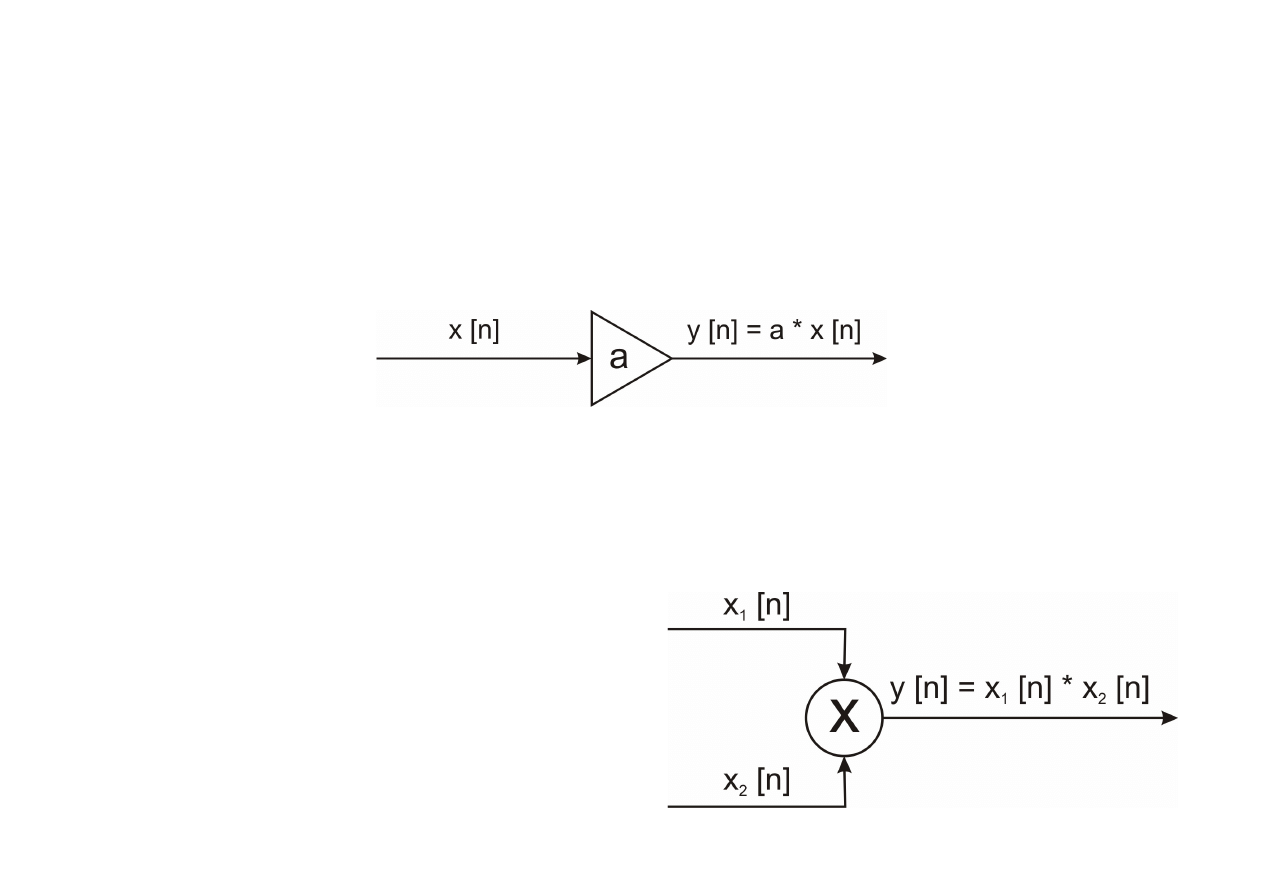
Wzmacniacz

Wzmacniacz jest bezpamięciowym układem realizującym operację skalowania

wartości próbek o stały czynnik a:

y [n]=a⋅x [n]

Układ mnożący (modulator)

Bezpamięciowy układ realizujący operację mnożenia wartości próbek ciągów

wejściowych:

y [n]=x

1

[

n]⋅x

2

[

n]

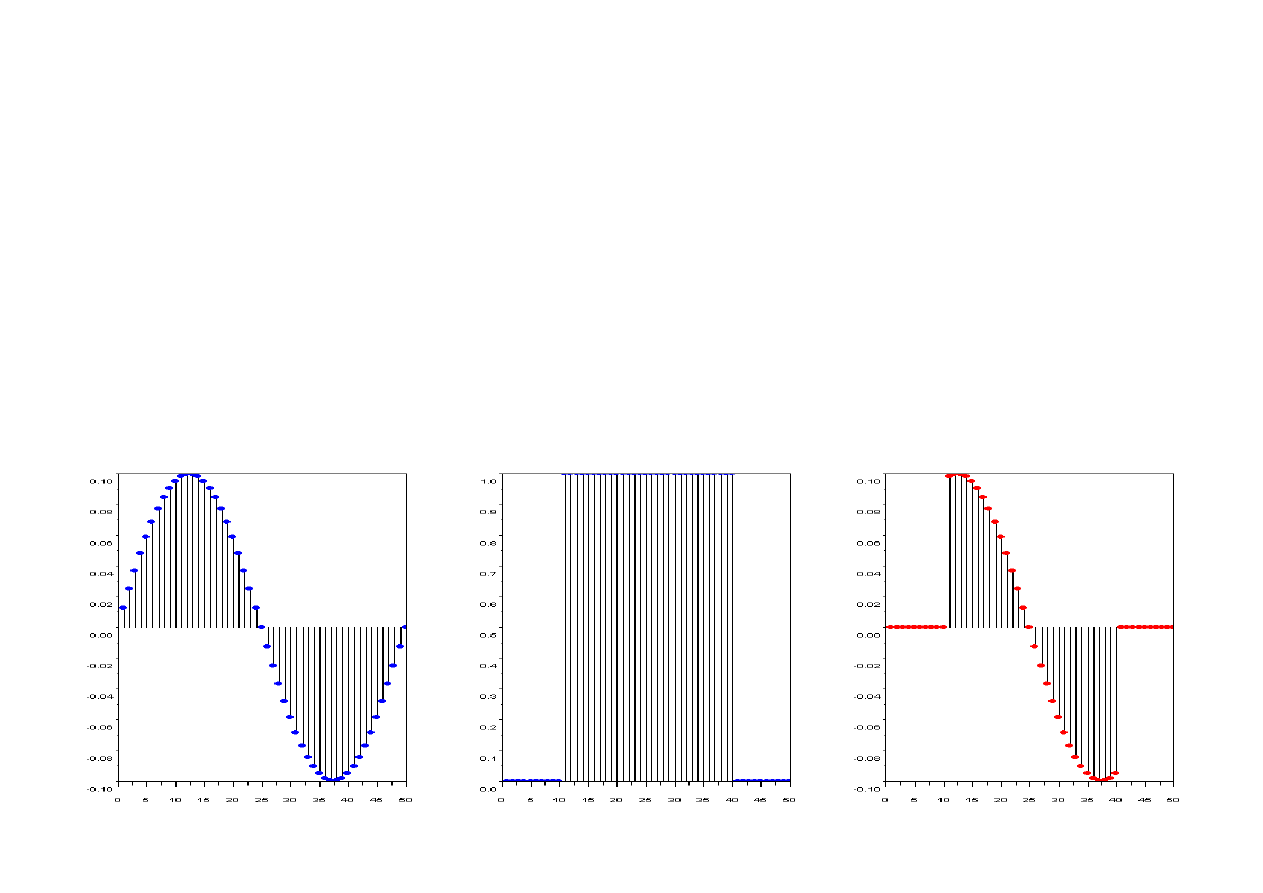
Zastosowania układu mnożącego – okienkowanie sygnału

Układy mnożące wykorzystuje się m.in. do tworzenia skończonych ciągów

sygnałów z ciągów nieskończonych na drodze mnożenia tych ostatnich przez ciąg

nazywany funkcją okna. Proces ten, zwany okienkowaniem (windowing),

odgrywa istotną rolę przy projektowaniu pewnych typów filtrów cyfrowych.

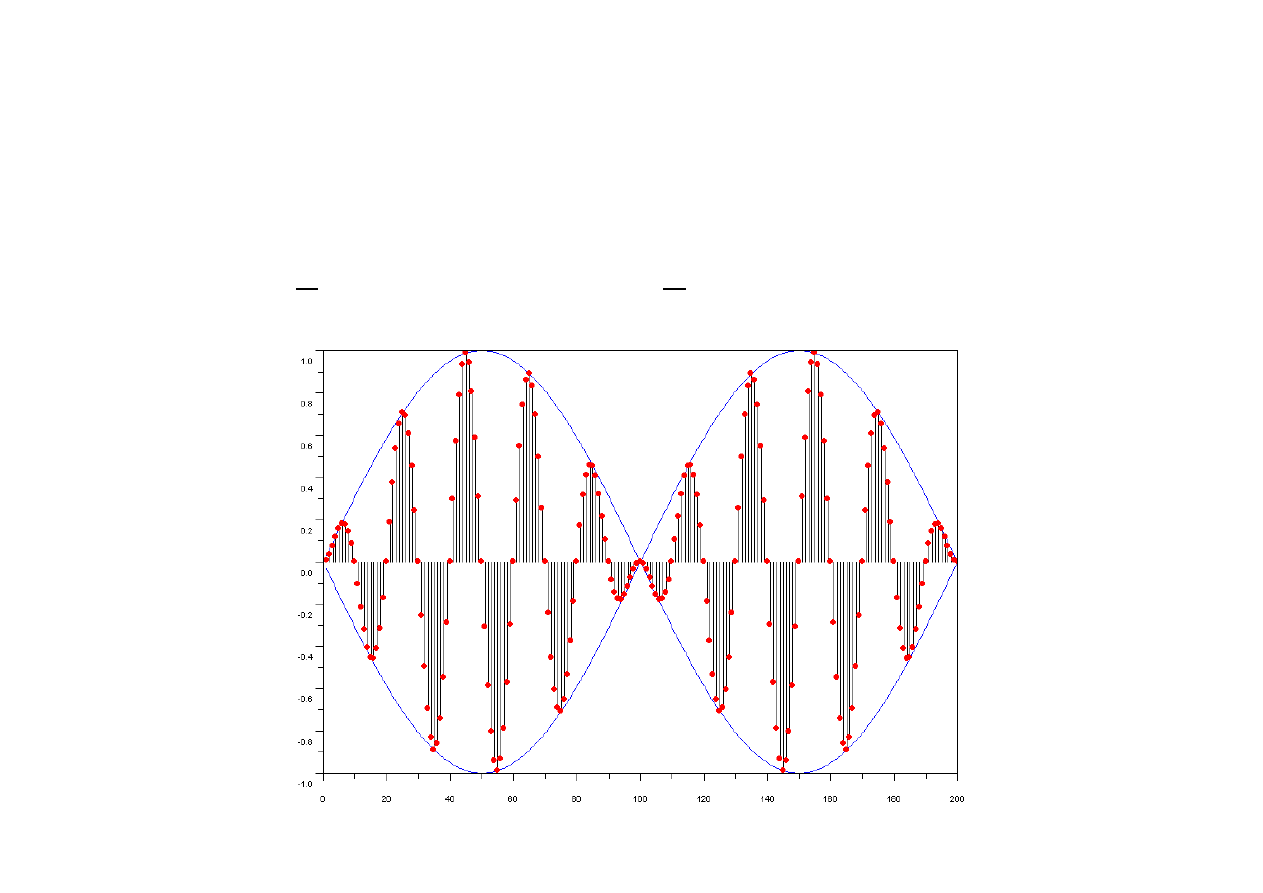
Zastosowania układu mnożącego – modulacja AM

Układ mnożący dwa wejściowe ciągi sinusoidalne wytwarza ciąg y[n] taki, że:

y [n]= x

1

[

n]⋅x

2

[

n]=cos2⋅⋅f

1

⋅

n⋅cos2⋅⋅f

2

⋅

n=...

...

1
2

cos2⋅⋅ f

1



f

2

⋅

n

1

2

cos2⋅⋅ f

1

−

f

2

⋅

n

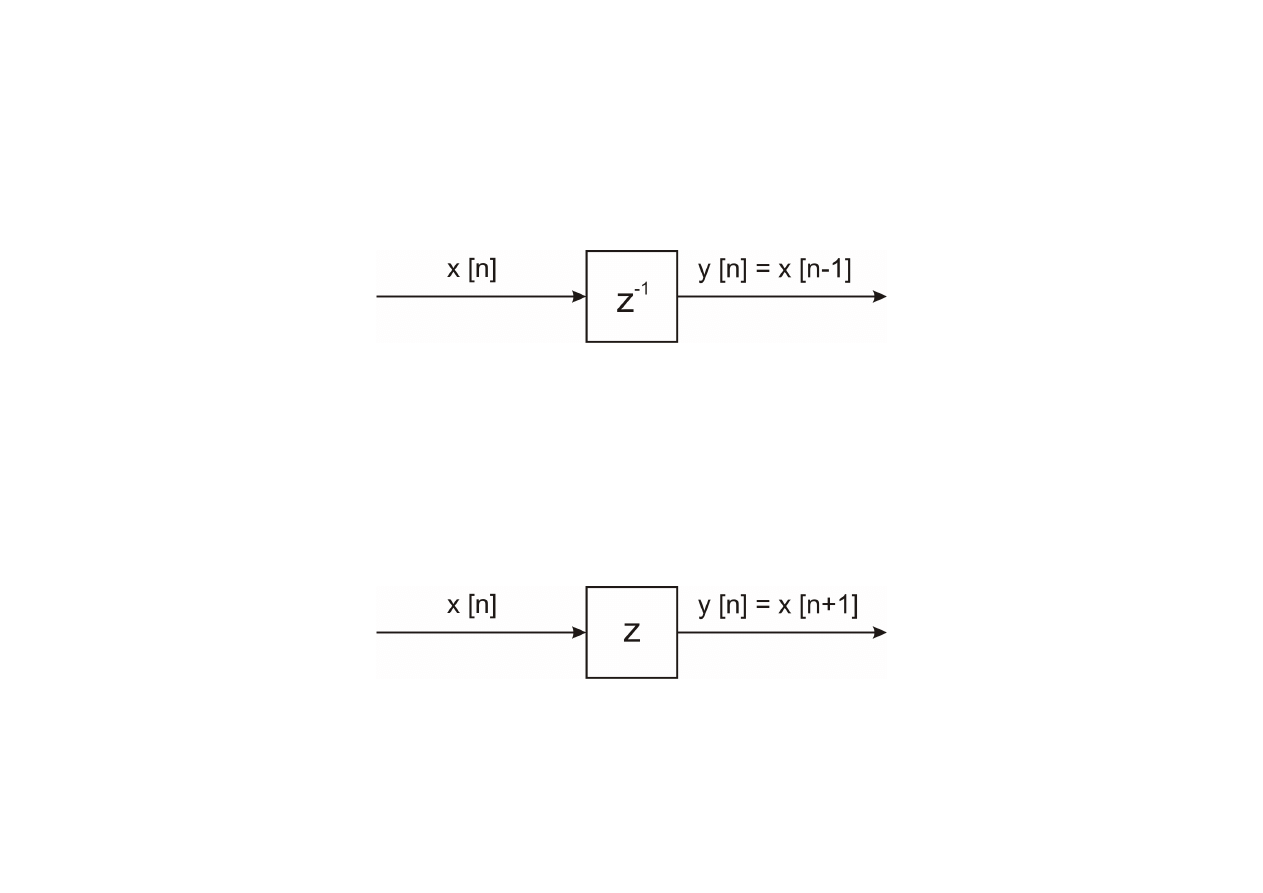
Układ opóźniający

Układ z pamięcią (rejestrem przesuwającym), który opóźnia ciąg wejściowy

o jedną próbkę, tzn.: y [n] = x [n-1].

Układ przyspieszający

Układ z pamięcią (rejestrem przesuwającym), który przyspiesza ciąg wejściowy

o jedną próbkę, tzn.: y [n] = x [n+1].

Przyspieszenie sygnału w czasie oznacza w istocie wcześniejsze zapisanie go

w całości i przywoływanie z pamięci w celu wykonania operacji.

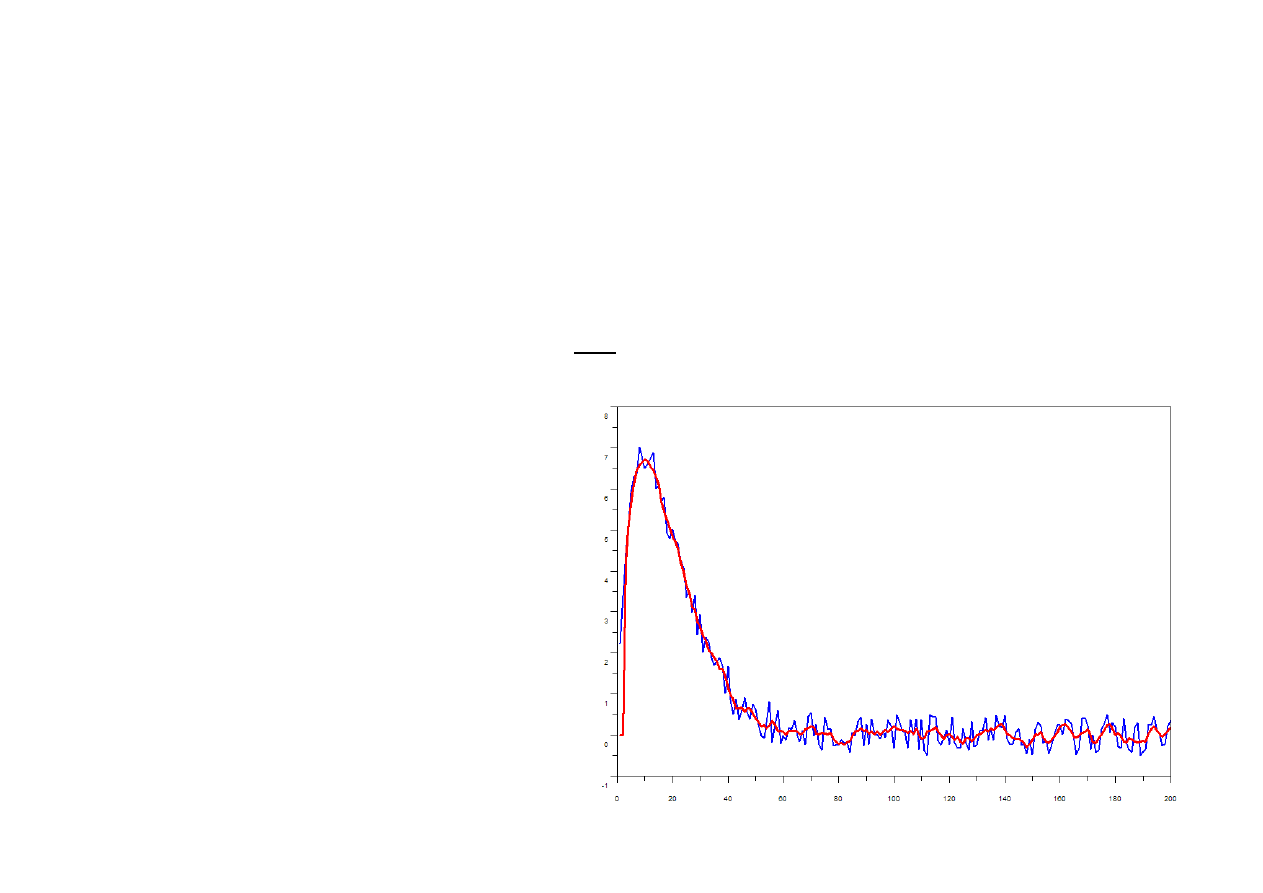
Zastosowania układów przesuwających – filtry biegnące

W przypadkach, gdy w celu wyeliminowania szumów nie można wielokrotnie

powtarzać pomiarów, do wygładzania przebiegów stosuje się filtry biegnące,

których zadaniem jest uśrednianie wartości M-sąsiednich próbek sygnału:

y [n]=

1

M

∑

k=0

M

x [n−k ]

Wygładzenie przebiegu zaszumionego

po zastosowaniu 5-punktowego filtru

biegnącego z układami

przesuwającymi.

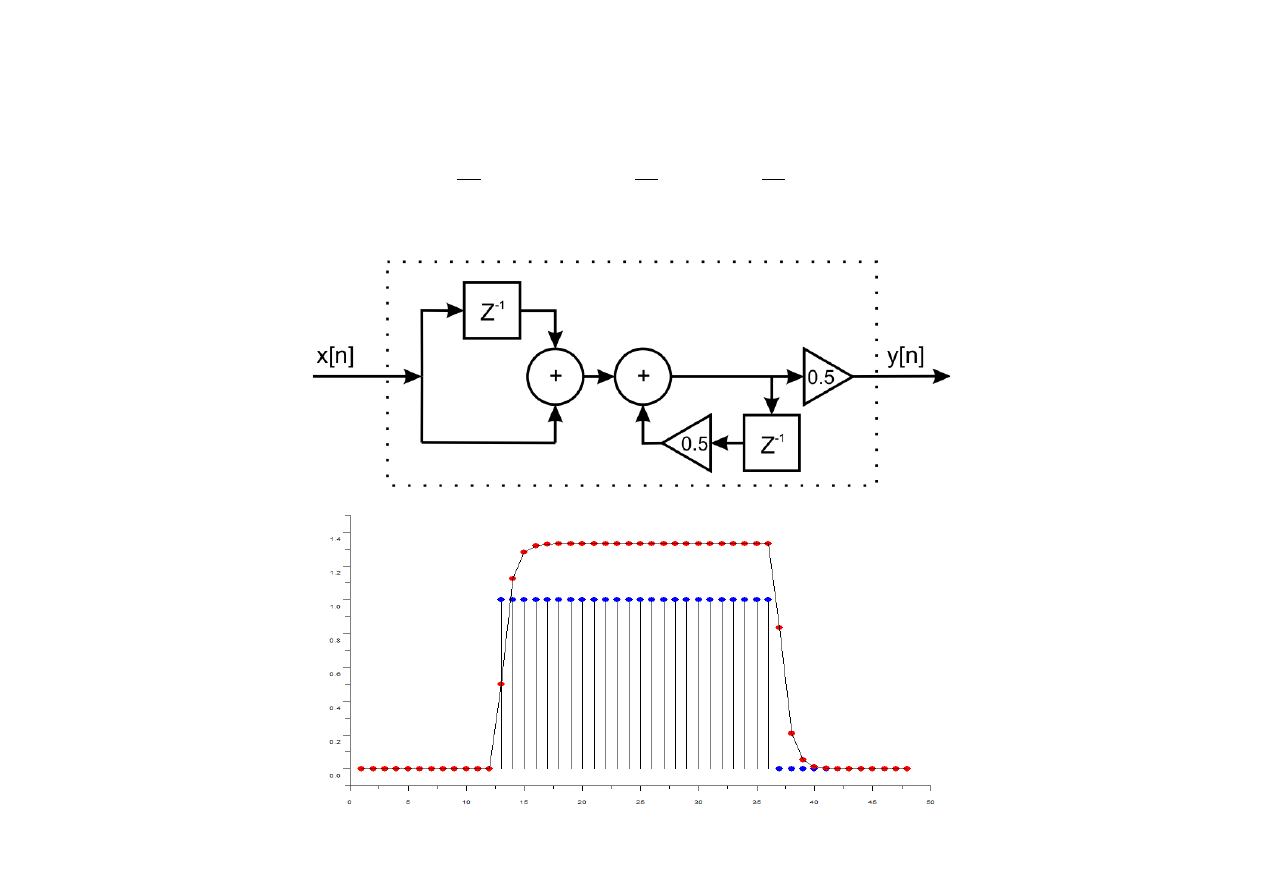
Ex.: Zbudować diagram blokowy układu czasu dyskretnego opisanego relacją:

y [n]=

1
4

y [n−1]

1
2

x [n]

1
2

x [n−1]

Klasyfikacja układów czasu dyskretnego

Do analizy i projektowania układów przetwarzania sygnału przydatny jest wstępny

podział według ogólnych własności, jakie te układy wykazują, bowiem silnie

rzutuje to na metody ich modelowania matematycznego.

W dalszym ciągu analizowane będą wyłącznie układu, których charakterystyki nie

zależą od wyboru sygnału wejściowego. Wystarczy zatem, że dana własność

układu nie jest spełniona dla pewnego sygnału, aby twierdzić, że układ ten nie

posiada tejże własności.

Układy statyczne i dynamiczne

Układ czasu dyskretnego nazywany jest statycznym (bezpamięciowym), jeśli

wartość dowolnej próbki n sygnału wyjściowego zależy wyłącznie od wartości

próbki sygnału wejściowego o tym samym indeksie:

y [n]=T n , x [n]

Układy statyczne nie wymagają zatem elementów opóźniających.

Z drugiej strony, układ jest dynamiczny (z pamięcią), jeśli stan jego wyjścia

w chwili n jest całkowicie opisany przez próbki sygnału wejściowego z przedziału

(n-N, n):

y [n]=T n , x n−N  , x n−N 1 ,... x n , N ≥0

Wartość N określa wielkość pamięci:

–

jeśli

0≤ N ∞

, to układ posiada skończoną pamięć o rozmiarze N,

–

jeśli

N =∞

, to układ posiada pamięć nieskończoną.

Układy niezmiennicze względem czasu

Układ jest niezmienniczy względem czasu (time-invariant TI) wtedy i tylko

wtedy, gdy jego charakterystyka I/O nie zmienia się w czasie, tzn. odpowiedź

układu na określone pobudzenie nie zależy od przesunięcia sygnału wejściowego

w czasie:

∀

k ∈ℤ

∀

{

x [n]}



y [n]=T  x [n]



⇒



y [n−k ]=T  x [n−k ]



Powyższa definicja specyfikuje test na niezmienniczość układu w czasie:

obliczamy odpowiedź układu y[n,k] na pobudzenie przesunięte w czasie x[n-k],

obliczamy przesuniętą odpowiedź y[n-k] i sprawdzamy, czy y[n,k] = y[n-k] dla

wszystkich możliwych wartości k. Jeśli tak, układ jest niezmienniczy w czasie, jeśli

nie – układ nie jest niezmienniczy (Time-Variant TV).

Przykłady układów TI oraz TV

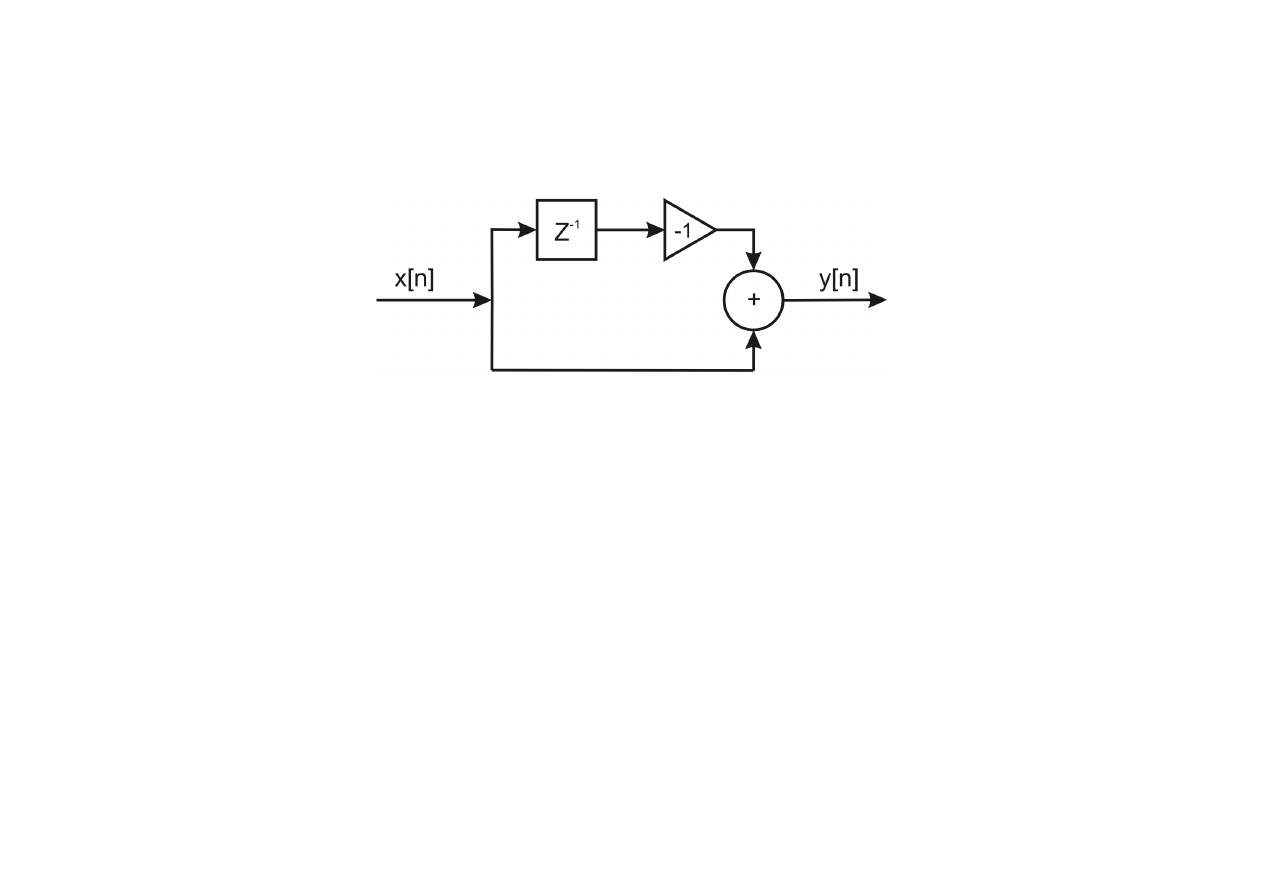
(1) Układ różniczkujący:

Układ opisany jest równaniem:

y [n]=x [n]− x [n−1]

Jeśli sygnał wejściowy zostanie opóźniony o k-próbek, wówczas:

y [n , k ]=T  x [n−k ]=x [n−k ]−x [ n−k −1]

Z drugiej strony:

y [n−k ]=x [n−k ]− x [n−1−k ]=x [ n−k ]− x [n−k −1]= y [n , k ]

Układ jest więc niezmienniczy w czasie.

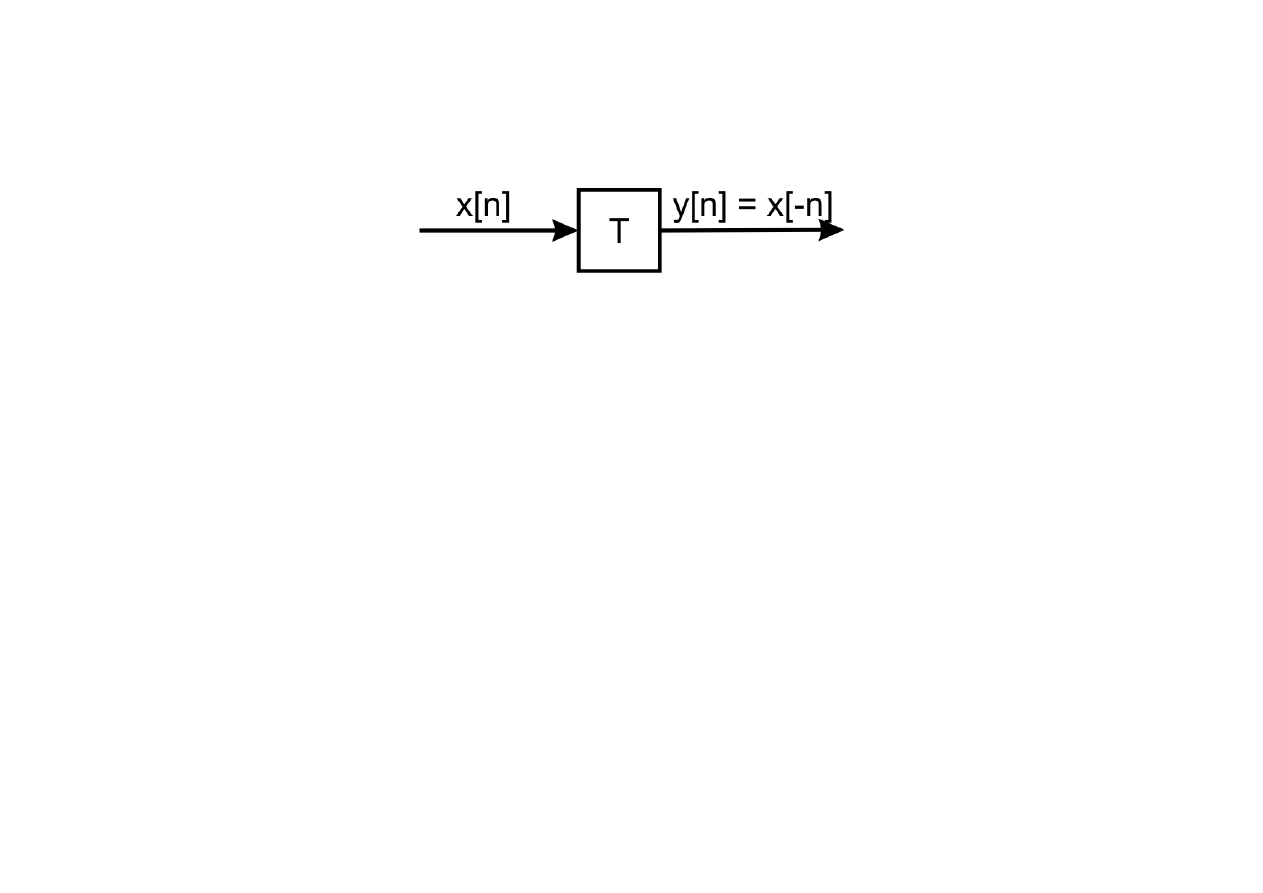
(2) Układ zawijający:

Układ opisany jest następującą relacją:

y [n]=T



x [n]



=

x [−n]

Odpowiedź układu na opóźnione pobudzenie x[n-k] wynosi:

y [n , k ]=T



x [n−k ]



=

x [−nk ]

Z drugiej strony, przesunięta odpowiedź ma postać:

y [n−k ]=x [−n−k ]≠ y [n , k ]

Układ nie jest więc niezmienniczy w czasie.

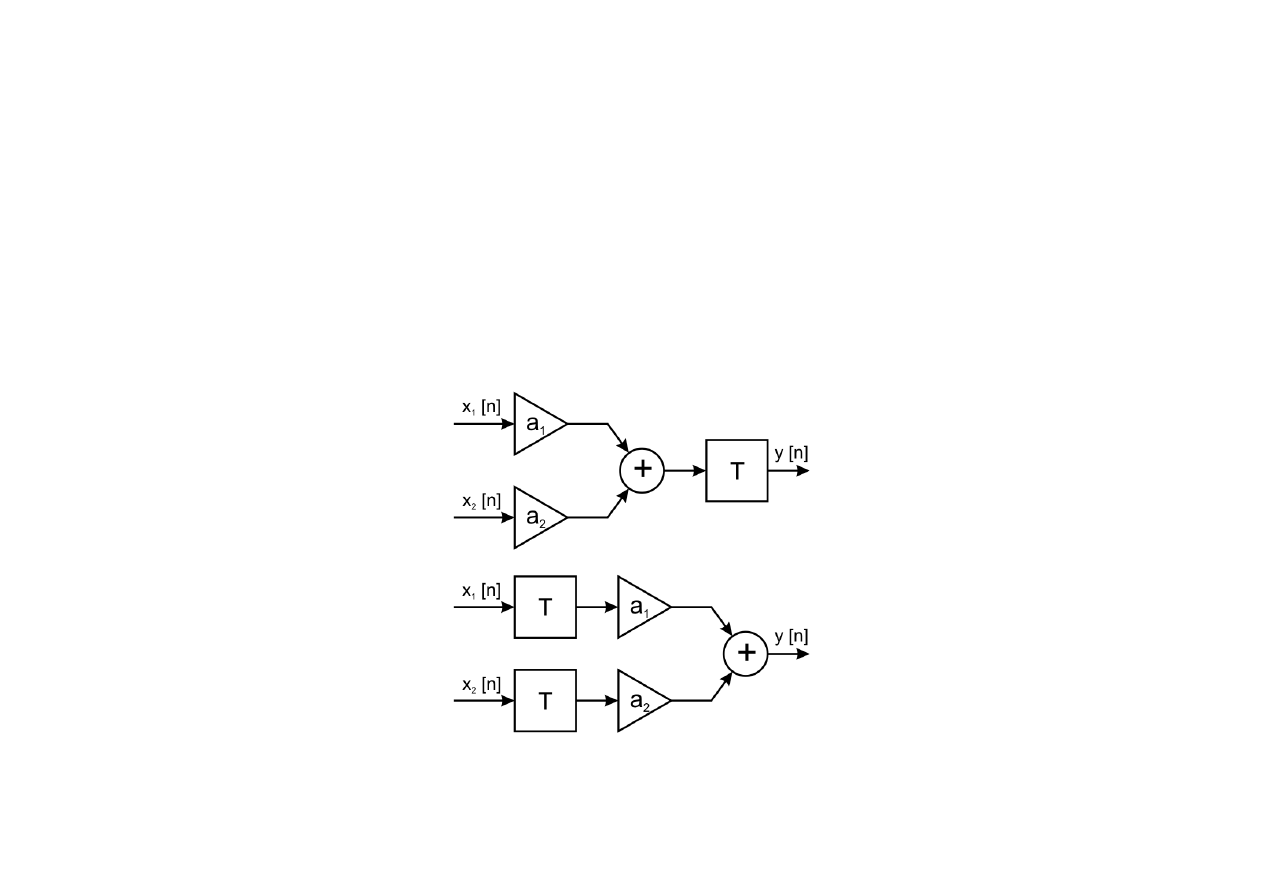
Układy liniowe i nieliniowe

Układy liniowe (Linear Systems – LS) stanowią grupę układów spełniających

zasadę superpozycji: kombinacja liniowa pobudzeń daje identyczną kombinację

liniową odpowiedzi:

∀

a

1,

a

2

∈ℂ

∀

{

x

1

[

n]}, {x

2

[

n]}

T a

1

⋅

x

1

[

n]a

2

⋅

x

2

[

n]=a

1

⋅

T  x

1

[

n]a

2

⋅

T  x

2

[

n]

Układy nie spełniające powyższego warunku są układami nieliniowymi.

Konsekwencje liniowości układów

(1) Układy liniowe są skalowalne:

Jeśli a

2

= 0, wówczas:

T a

1

⋅

x

1

[

n]=a

1

⋅

T  x

1

[

n]=a

1

⋅

y

1

[

n]

Wynika stąd, że dowolne przeskalowanie pobudzenia powoduje proporcjonalną

zmianę odpowiedzi układu.

(2) Układy liniowe są addytywne:

Jeśli a

1

= a

2

= 1, wówczas:

T  x

1

[

n] x

2

[

n]=T  x

1

[

n]T  x

2

[

n]= y

1

[

n] y

2

[

n]

Liniowość układów sprawia, że odpowiedź na dowolne pobudzenie może

Liniowość układów sprawia, że odpowiedź na dowolne pobudzenie może

być wyznaczona na podstawie odpowiedzi na pewne sygnały standardowe

być wyznaczona na podstawie odpowiedzi na pewne sygnały standardowe

(impuls jednostkowy, skok itp.)

(impuls jednostkowy, skok itp.)

Przykłady układów liniowych i nieliniowych

(1) Dany jest układ opisany relacją:

y [n]= x [n

2

]

Dla dwóch dowolnych ciągów wejściowych x

1

[n] oraz x

2

[n], jak też dowolnych

współczynników a

1

, a

2

zachodzi:

T a

1

⋅

x

1

[

n]a

2

⋅

x

2

[

n]=a

1

⋅

x

1

[

n

2

]

a

2

⋅

x

2

[

n

2

]=

...

a

1

⋅

T  x

1

[

n]a

2

⋅

T  x

2

[

n]

Układ jest więc liniowy.

(2) Dany jest układ opisany relacją:

y [n]= x

2

[

n]

Zachodzi dla niego:

T a

1

⋅

x

1

[

n]a

2

⋅

x

2

[

n]=a

1

2

⋅

x

1

2

[

n]a

2

2

⋅

x

2

2

[

n]

a

1

⋅

T  x

1

[

n]a

2

⋅

T  x

2

[

n]=a

1

⋅

x

1

2

[

n]a

2

⋅

x

2

2

[

n]

Układ jest zatem nieliniowy.

Układy przyczynowe i nieprzyczynowe

Układ nazywa się przyczynowym (causal system) jeśli jego odpowiedź

w dowolnej chwili czasu zależy wyłącznie od aktualnego i poprzednich stanów

wejścia:

∀

{

x [n]}

y [n]=T  x n , x n−1 , x n−2 ,...

Ukłądy nie spełanijące powyższego warunku są układami nieprzyczynowymi

(noncausal systems), których odpowiedź zależy nie tylko od aktualnego i

przeszłego, ale również od przyszłego stanu wejścia.

Układów nieprzyczynowych nie można zrealizować jako układów czasu

rzeczywistego – do przetwarzania przyszłych próbek sygnału należy

zarejestrować uprzednio cały sygnał.

Układy stabilne i niestabilne

Stabilność układów jest cechą niezwykle ważną z punktu widzenia ich praktycznej

przydatności. Układy niestabilne wykazują zachowania niepożądane, jak np.

generują znaczące błędy, gwałtownie reagują na niewielkie zmiany pobudzenia,

czy też powodują przepełnienie zakresu przetwarzanych próbek.

Układ nazywa się stabilnym w sensie BIBO (Bounded Input – Bounded Output

Stable System), wtedy i tylko wtedy, gdy skończone pobudzenie generuje

skończoną odpowiedź:

∀

n

∃

M

x

, M

y



{

x [n]}≤M

x

∞



⇒



{

y [n]}≤M

y

∞



Jeśli powyższy warunek nie jest spełniony, układ jest niestabilny (unstable

system).

Ex.: Sprawdźmy stabilność układu nieliniowego opisanego zależnością:

y [n]= y

2

[

n−1] x [n]

Jako sygnał ograniczony wybierzmy:

x [n]=C⋅[n] ,C ∈ℤ ,∣C∣∞

Załóżmy ponadto, że:

y [−1]=0

Wówczas odpowiedź układu ma postać:

y [0]=C ,
y [1]=C

2,

y [2]=C

4,

y [n]=C

2⋅n

Układ jest stabilny w sensie BIBO, gdy

∣

C∣≤1

, jeśli jednak

∣

C∣1

układ staje

się niestabilny.

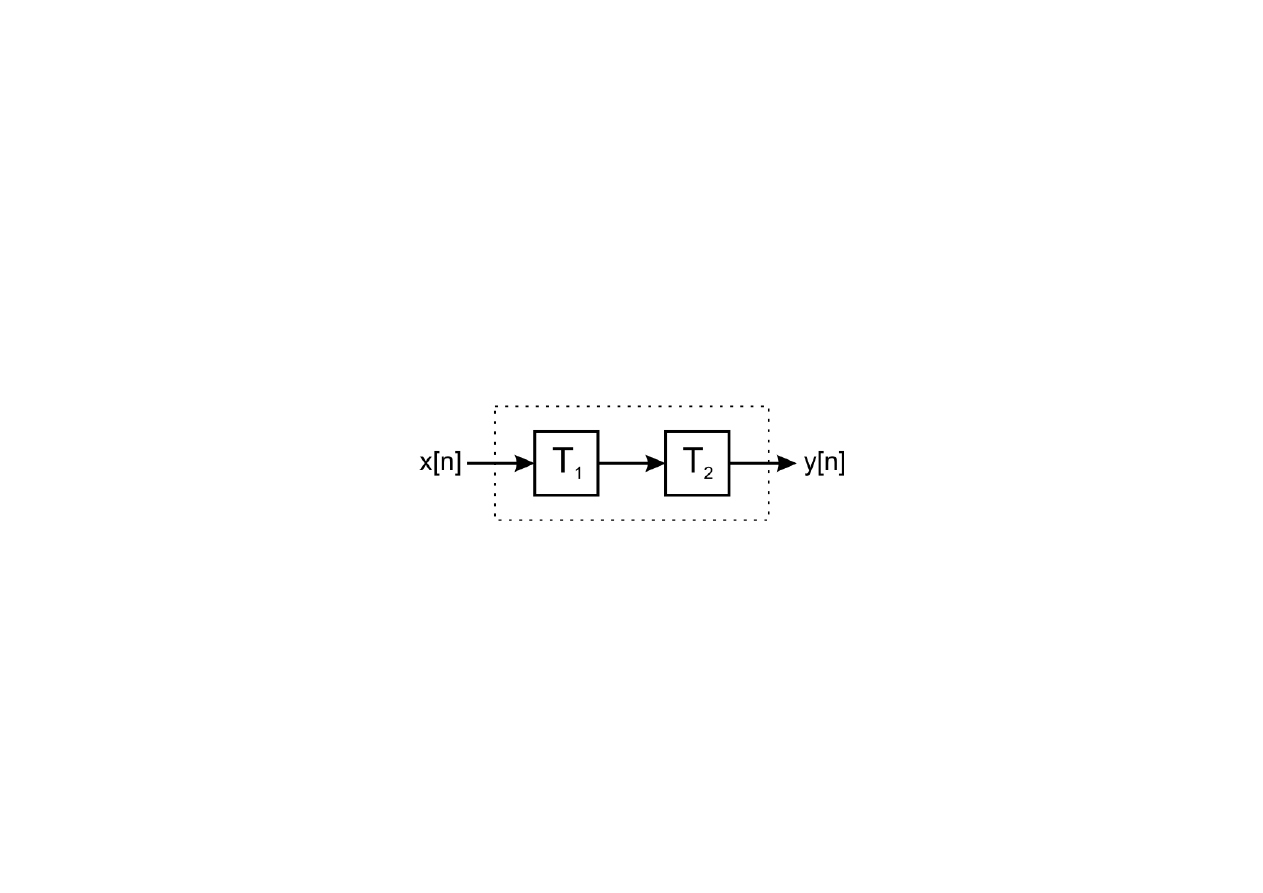
Łączenie układów

Układy czasu dyskretnego można łączyć w większe bloki. Istnieją dwa

podstawowe sposoby połączeń: kaskadowe (szeregowe) oraz równoległe,

z których każdy daje w wyniku inną charakterystykę wypadkową układu.

(1) Połączenie szeregowe (kaskadowe):

Wypadkowa odpowiedź układów na pobudzenie x[n] wynosi:

y [n]=T

2



T

1



x [n]





Układy T

2

oraz T

1

mogą być zatem połączone w jeden układ T

s

:

T

s

=

T

2

⋅

T

1

Przemienność operacji kaskadowych

W ogólności, istotna jest kolejność kaskadowego łączenia układów, bowiem:

T

2

⋅

T

1

≠

T

1

⋅

T

2

Twierdzenie

Jeśli układy T

1

oraz T

2

są liniowe i niezmiennicze w czasie (Linear Time-Invariant

– LTI), wówczas układ T

C

jest niezmienniczy w czasie i przemienny:

T

2



T

1



x [ n−k ]=T

2



y

1

[

n−k ]= y [n−k ]

Przemienność układów LTI wynika z definicji ich odpowiedzi jako splotu

pobudzenia i charakterystyki I/O.

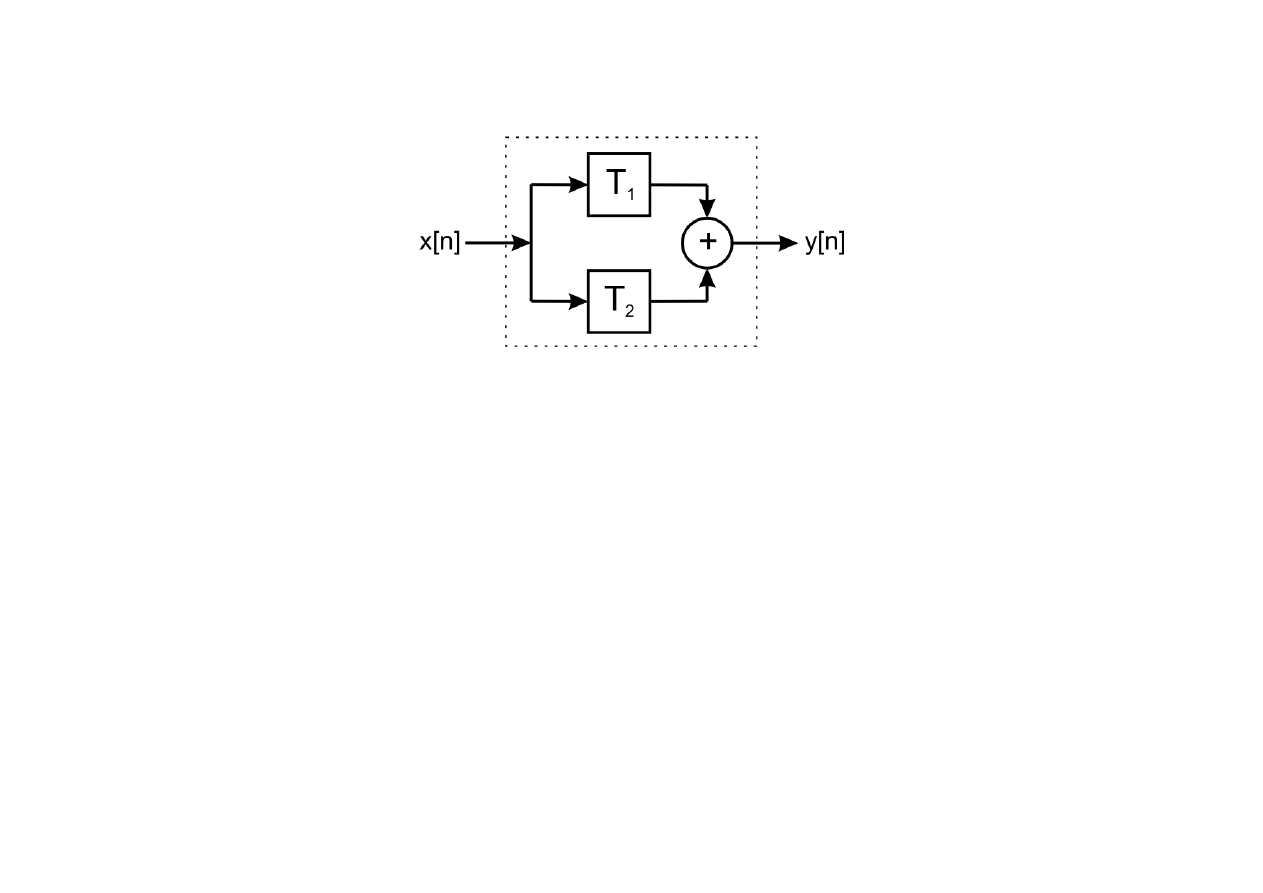
(2) Połączenie równoległe:

Odpowiedź układu na pobudzenie x[n] ma postać:

y [n]=T

1



x [n]T

2



x [n]= y

1

[

n] y

2

[

n]=T

1



T

2



x [n]=T

p



x [n]

Możliwość łączenia układów pozwala konstruować układy złożone z bloków

podstawowych, ale z drugiej strony – pozwala także dzielić układy złożone na

prostsze funkcjonalnie bloki w celu ich późniejszej analizy.

Odpowiedź impulsowa i skokowa filtrów cyfrowych

Odpowiedzią impulsową filtru cyfrowego (impulse response) jest odpowiedź

tego filtru na pobudzenie impulsem jednostkowym:

h[n]=T [n]

Analogicznie, odpowiedzią skokową (step response) filtru cyfrowego jest ciąg

będący odpowiedzią na pobudzenie skokiem jednostkowym:

s[n]=T [n]

Ex.: Znaleźć odpowiedź impulsową układu:

y [n]=a

1

⋅

x [n−1]a

2

⋅

x [n]

Odpowiedź impulsowa h[n] jest odpowiedzią na pobudzenie impulsem

jednostkowym, tak więc:

h[n]=a

1

⋅[

n−1]a

2

⋅[

n]={a

1,

a

2

}

Analiza układów LTI czasu dyskretnego w dziedzinie czasu

Istnieją dwie podstawowe metody analizy układów LTI czasu dyskretnego

w dziedzinie czasu:

–

poprzez rozwiązanie równania różnicowego opisującego zależność

wejściowo-wyjściową,

–

określenie wypadkowej odpowiedzi układu (splotu) na pobudzenie będące

kombinacją liniową sygnałów elementarnych

Konsekwencją liniowości i niezmienniczości w czasie układów LTI czasu

Konsekwencją liniowości i niezmienniczości w czasie układów LTI czasu

dyskretnego jest fakt, iż układy takie są w pełni opisywane poprzez podanie

dyskretnego jest fakt, iż układy takie są w pełni opisywane poprzez podanie

ich odpowiedzi impulsowej h[n].

ich odpowiedzi impulsowej h[n].

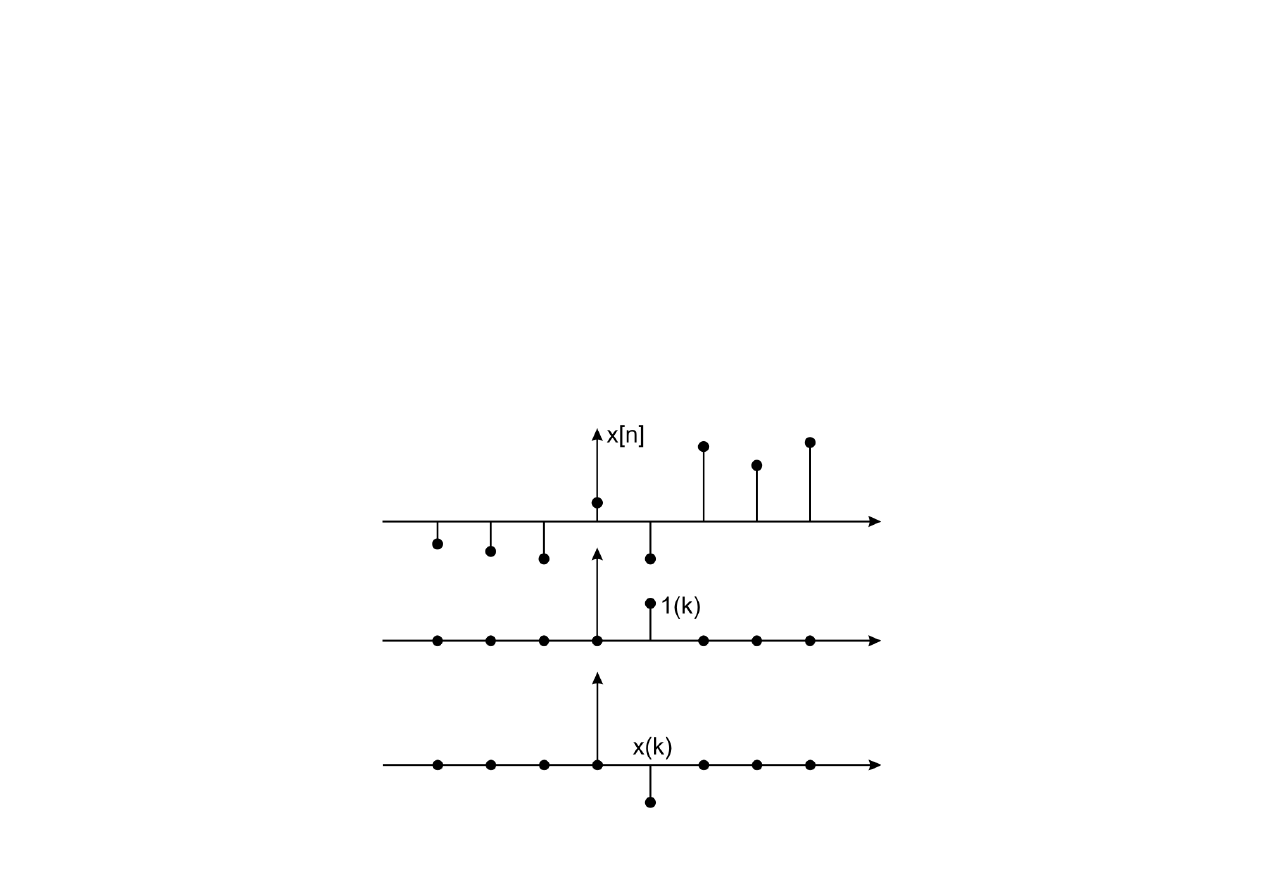
Dekompozycja sygnału

Niech x[n] będzie dowolnym ciągiem w przestrzeni H, zaś

{

k

[

n]}={[ n−k ]}

-

bazą tej przestrzeni. Sygnał x[n] daje się wówczas rozwinąć w bazie w postaci:

x [n]=

∑

k =−∞

∞

x [k ]⋅[n−k ]

gdzie wartości x[k] stanowią wagi próbek ciągu.

Odpowiedź układu liniowego na dowolne pobudzenie

Oznaczmy odpowiedź układu liniowego na pobudzenie impulsem jednostkowym

jako:

y [n , k ]=T [n−k ]≡h[n , k ]

Odpowiedź tego samego układu na dowolne pobudzenie będące kombinacją

liniową impulsów jednostkowych wynosi:

y [n]=T



∑

k =−∞

∞

x [ k ]⋅[n−k ]



=

∑

k =−∞

∞

x [k ]⋅T



[

n−k ]



=

∑

k =−∞

∞

x [k ]⋅h[n , k ]

Powyższe wyrażenie jest prawdziwe dla dowolnego układu liniowego (zarówno

TI, jak i TV).

Splot sygnałów

W przypadku układów LTI, odpowiedź na pobudzenie będące kombinacją

przesuniętych impulsów jednostkowych upraszcza się do postaci:

y [n]=T 

∑

k =−∞

∞

x [k ]⋅[n−k ]=

∑

k =−∞

∞

x [ k ]⋅h[n−k ]= x [n]°h[n]

Powyższe wyrażenie określa się mianem splotu sygnałów (convolution sum).

Kolejność działań w przypadku obliczania splotu:

–

Zawijanie (folding) ciągu h[n] → h[-n],

–

Przesunięcie ciągu h[-n] o k-próbek → h[k-n],

–

Wymnożenie odpowiednich próbek ciągów x[n] oraz h[k-n] → x[n]∙h[k-n],

–

Wysumowanie wszystkich iloczynów x[n]∙h[k-n], aby otrzymać wartość splotu

dla n

0

= k → y[n

0

] = x[n]∙h[n

0

–

n].