Więzy

Więzami są ograniczenia nałożone na ruch układu (na współrzędne lub prędkości punktów lub brył
układu). Można je wyrazić w postaci zależności analitycznych nazywanych równaniami więzów.

Klasyfikacja więzów i ich podział z uwzględnieniem zastosowań



więzy geometryczne– nakładanie ograniczeń na położenie poszczególnych poszczególnych
elementów danego układu

=

,

,

,

, … ,

, … ,

= 0,

= 1, … , = 1, … , <



więzy kinematyczne- nakładanie ograniczeń na położenie poszczególnych poszczególnych
elementów danego układu, na składowe prędkości i przyspieszenia, a także na zmianę
prędkości i przyspieszenia

=

,

,

, … ,

, ̇ , ̇ , … , ̇ , … ,

( )

,

( )

, … ,

( )

= 0,

= 1, … ,



więzy

holonomiczne – więzy całkowalne



więzy nie

holonomiczne – więzy niecałkowalne



więzy reonomiczne – zależą jawnie od czasu

=

,

,

,

, … ,

, … ,

= 0



więzy skleronomiczne – nie zależą jawnie od czasu

=

,

,

, … ,

, … ,

= 0



więzy dwustronne – gdy więzy opisane są równaniem

=

,

,

,

, … ,

, … ,

= 0



więzy jednostronne – gdy więzy opisane są nierównością

=

,

,

,

, … ,

, … ,

≥ 0



więzy idealne(doskonałe) – praca reakcji na przesunięciach przygotowanych jest równa zeru:

∗

= 0

−

ę

ℎ ł

ℎ (

ę ó )



więzy rzeczywiste – wywołuje siłę tarcia

∗

> 0

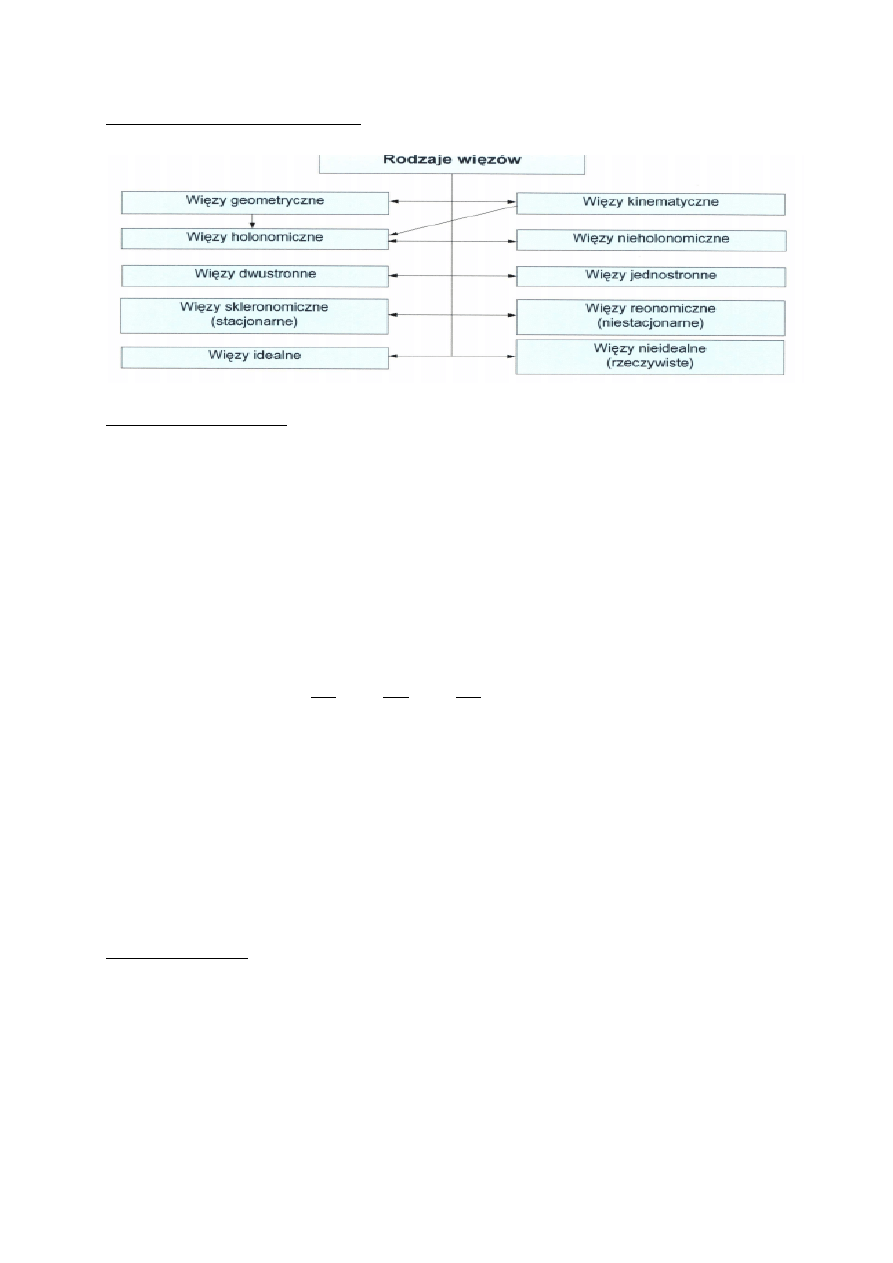
Podział z uwzględnieniem zastosowań

Przemieszczenie wirtualne
Za przemieszczenie wirtualne przyjmuje dowolne małe przemieszczenie, które nie jest zależne od
czasu i siły zewnętrzne na jej drodze nie zmieniają wartości.

Przemiesczenie przygotowane lub wirtualne nazywamy każdy wektor δr

υ

(δx

υ

, δy

υ

, δz

υ

) (υ= 1,…,n)

spełniający układ równań

δr ∗ grad

= 0,

= 1, … ,

Oznacza to, że współrzędne δx

υ

, δy

υ

, δz

υ

(υ= 1,…,n) wektorów δr

υ

(υ= 1,…,n), będące wariacjami

współrzędnych, spełniają układ równań

δ

=

∂

∂x

δx +

∂

∂y

δy +

∂
∂z

δz

= 0,

= 1, … ,

Przemieszczenie wirtualne(przygotowane) musi spełniać kilka bardzo ważnych warunków, musi być:



pomyślane,



możliwe (kinematycznie dopuszczalne),



niezależne od czynników zewnętrznych(np. obciążeń),



bardzo małe w porównaniu z wymiarami ciała,



niezależne od czasu,



ciągłe (co najmniej raz różniczkowalne).

Obciążenie wirtualne

Obciążenie musi spełniać kilka bardzo ważnych warunków, musi być:



pomyślane,



możliwe (kinematycznie dopuszczalne),



niezależne od czynników zewnętrznych(np. obciążeń),



bardzo małe w porównaniu z wymiarów i obciążeń zewnętrznych,



niezależne od czasu,



nie musi być ciągłe (może być punktowe) – zasada Saint-Venanta.

Praca wirtualna

Gdy układ punktów jest w równowadze wtedy siły zewnętrzne i reakcje są w równowadze:

= ⃗ + ⃗ = 0,

= 1, … ,

Praca sił

na przesunięciach przygotowanych punktów

, czyli tak zwana praca przygotowana

jest równa

=

⃗ ∙ ⃗ +

⃗ ∙

⃗ = 0

Więzy są doskonałe więc równanie pracy przygotowanej przyjmuje postać:

=

⃗ ∙

⃗

Zasada prac przygotowanych

Jeśli układ n punktów materialnych jest skrępowany więzami holonomicznymi, skleronomicznymi,
dwustronnymi i doskonałymi, to warunkiem koniecznym i dostatecznym równowagi układu jest, aby
praca sił zewnętrznych F

1

,…,F

n

na przesunięciach przygotowanych δr

1

,…, δr

n

, czyli praca

przygotowana sił zewnętrznych była równa zeru.

⃗ ∙

⃗ = 0

Współrzędne uogólnione

Współrzędne uogólnione, to minimalna liczba współrzędnych niezależnych od siebie, opisujących w
sposób jednoznaczny położenie układu w przestrzeni. Minimalna ilość liczb współrzędnych bierze się
z ilości stopni swobody ma rozpatrywany układ . Najczęściej współrzędne uogólnione przyjmują
postać przemieszczeń. Mogą to być zarówno przemieszczenia liniowe (translacyjne), jak i kątowe
(rotacyjne).
Liczbę stopni swobody p wyznaczamy poprzez wyznaczenie sumy liczb stopni swobody
poszczególnych punktów materialnych. Od tej sumy odejmujemy liczbę równań więzów.
Współrzędne uogólnione oznaczone są , = 1, … , .

Współrzędne uogólnione powinny spełniać dwa warunki:



wektory wodzące punktów materialnych powinny być jednoznacznymi funkcjami
uogólnionych współrzędnych



współrzędne uogólnione

i

q

powinny być wybrane zgodnie z równaniami więzów

Położenie układu określająca dowolne współrzędne kartezjańskie za pomocą współrzędnych
uogólnionych określamy za pomocą

=

,

,

,

, … ,

Przemieszczenie wirtualne w współrzędnych uogólnionych występuje w postaci:

=

Siła uogólniona

Jest to siła która wykonuje pracę w tej samej przestrzeni co odpowiadające im przemieszczenia
uogólnione.
Praca wirtualna:

=

Zależność dla więzów:

=

Z tych dwóch zależności otrzymujemy wzór pracy wirtualnej z przemieszczeniem wirtualnym z
współrzędnymi uogólnionymi:

=

=

=

Siłę uogólnioną możemy również wyznaczyć wykorzystując zasadę d’Alemberta

Zasada d’Alemberta
Jeżeli układ punktów jest skrępowany więzami holonomicznymi i nieholonomicznymi
dwustronnymi (mogą one być reonomiczne) i doskonałymi, to praca sił zewnętrznych i sił
bezwładności na przesunięciach przygotowanych jest równa zeru.

Wykorzystując równanie d’Alemberta dla układu punktów materialnych o więzach holonomicznych,
dwustronnych i idealnych w układzie inercjalnym o postaci

−

̈

= 0

otrzymujemy:

−

̈

= 0

−

̈

= 0

Powyższe równanie zapiszemy w inny sposób w celu ułatwienia dalszych działań:

−

̈

= 0, = 1, … ,

Ostatnie równanie musi być spełnione dla dowolnego

( = 1, … , ). Aby to zachodziło,

wyrażenie zawarte w nawiasie kwadratowym tego równania musi być równe zero, czyli :

−

̈

= 0, = 1, … ,

=

̈

, = 1, … ,

W ostatnim równaniu po prawej stronie występuje wyrażenie, które stanowi odpowiednik siły
obciążającej układ zgodnie ze współrzędną

, ponieważ otrzymano je przy założeniu, że

przemieszczenie przygotowane

było różne od zera. Wyrażenie to nazywamy siłą uogólnioną

odpowiadającą -tej współrzędnej uogólnionej, którą definiujemy jako:

=

Praca wirtualna wykonana przez siły uogólnione, gdy są określone odpowiadającym im uogólnionym
przemieszczeniom wirtualnym wynosi:

=

Jeżeli przemieszczenie uogólnione są od siebie niezależne, to wówczas warunki równowagi statycznej
mogą być wyrażone za pomocą sił uogólnionych w następujący sposób:

= 0, = 1, … ,

Siła uogólniona w równaniach Eulera-Lagrange’a

Wykorzystując funkcję lagrange’a:

=

−

( , ̇ , ) = ( , ̇ , ) − ( , ̇ , )

gdzie:

−

−

Wykorzystując funkcję otrzymujemy równanie Eulera-Lagrange’a:

̇

−

= 0

Człon

̇

jest pędem uogólnionym i wyrazimy go za pomocą , człon

jest siłą uogólnioną .

Po podstawieniu członów do równania Eulera-Lagrange’a otrzymujemy:

=

Siła uogólniona przyjmuje postać w równaniu Eulera-Lagrange’a drugiego rodzaju:

̇

−

=

Energia potencjalna dla punktu materialnego
Praca wykonana z ogólnego stanu położenia A do odmiennego stanu położenia B.
Ogólne wyrażenie dla energii potencjalnej:

= −

+

+

Energia potencjalna dla układu punktów materialnych
Praca wykonana z ogólnego stanu położenia A do odmiennego stanu położenia B.
Ogólne wyrażenie dla energii potencjalnej:

= −

+

+

Energia kinetyczna punktu materialnego

=

1
2

Energia kinetyczna dla układu punktów materialnych
Energia kinetyczna układu punktów materialnych jest równa energii tegoż układu w jego ruchu
względem środka masy oraz energii kinetycznej masy całkowitej poruszającej się z prędkością
środka masy.

=

1
2

+

1
2

−

ę

ść

ę

ę

ł

ℎ

−

ę

ść

Energia kinetyczna ciała sztywnego

=

−

ł

ś

−

ę

ść ℎ

ł

Formułowanie różniczkowych równań ruchu dla zachowawczych układów mechanicznych za pomocą
równań Eulera-Lagrange’a

Energia kinetyczna w układzie zachowawczym jest taka sama w każdym cyklu. Nie działają inne siły.
Siła jest zachowawcza jeżeli praca wykonana przez tę siłę nad punktem materialnym, który porusza
się po dowolnej drodze zamkniętej, jest równa zeru.
Siły zachowawcze układu są to siły, które powodują, że wykonana przez te siły praca nad układem z
jednego jego stanu do drugiego zależy jedynie od początkowych i końcowych współrzędnych
punktów materialnych układu (jest niezależna od drogi).

= −

,

= 1, … ,

̇

−

=

̇

−

= −

Rodzaje sił zachowawczych:



kulombowskie siły oddziaływań elektrostatycznych



siła grawitacyjna (tylko w skrajnym polu grawitacyjnym)



siła sprężystości ciał doskonale sprężystych i wszystkie siły centralne

Siły dyssypacji energii w sformułowaniach Lagange’a – funkcja dyssypacji Rayleigha (jednorodna
forma kwadratowa prędkości uogólnionych)

Siła dyssypacji powoduje zmniejszenie energii znajdującej się w układzie.
Siłę dyssypacyjną mają charakter wiskotyczny, to znaczy są liniowo zależne od prędkości
uogólnionych i mogą być przedstawione w postaci: :

= −

̇ ,

∗ ̇

−

ół

ł

przy czym macierz współczynników jest symetryczna

=

.

Siły dyssypacyjne

można określić za pomocą tak zwanej dyssypacyjnej funkcji Rayleigha R, która

jest następującą jednorodną formą kwadratową prędkości uogólnionych:

=

1
2

̇ ,

∗ ̇ ∗ ̇

Wzór siły dyssypacyjnej możemy przedstawić:

= −

̇

Równanie ruchu w układzie dyssypacji jest w postaci

̇

−

=

̇

−

= −

̇

Funkcja Hamiltona.

Funkcja Hamiltona (hamiltonian) jest funkcją współrzędnych uogólnionych i pędów uogólnionych,
opisujący układ fizyczny.
Hamiltonian: ( ,

, ) = ∑

− ( ,

, ) +

= ∑

− ( ,

, )

Pęd uogólniony:

=

= ( , ̇ , )

Prędkość uogólniona: ̇ = ̇ ( ,

, )

Przekształcenie Legendre’a

Rozważmy funkcję dwóch zmiennych niezależnych z=f(x,y). Oznaczając

( , ) =

( , ) =

Możemy różniczkę zupełną tej funkcji napisać w postaci

=

+

Jeśli jako zmienne niezależne weźmiemy u i v, to x i y będą funkcjami zmiennych u i v

=

( , ),

=

( , )

Rozważmy teraz funkcję Z=Z(u,v) taką, że jej różniczka zupełna jest równa

( , ) =

( , ),

+

( , )

to znaczy

=

+

Funckję z będziemy nazywali funkcję tworzącą względem zmiennych x,y funkcję Z zaś funkcję

tworzącą względem zmiennych u,v. Przejście od zmiennych x,y do u,v i związane z tym przejście od
funkcji tworzącej z(x,y) do funckji tworzącej Z(u,v) nazywamy przekształceniem Legendre’a,

Kanoniczne równanie Hamiltona

=

(

̇ +

̇ ) −

+

̇

̇

−

=

̇

̇ =

=

̇ −

−

=

(

̇ − ̇

) −

=

̇

̇ +

̇

+

Kanoniczne równania:

̇ =

̇

̇ = −

̇

= −

Wartość pędu uogólnionego nie zmieniają się , gdy hamiltonian jest niezależny od współrzędnej
uogólnionej.

̇ = −

̇

= 0

Nawiasy Poissona

W układzie współrzędnych kanonicznych (zwanych również jako współrzędne Darboux) (q

i

,p

i

),

zdefiniowanych w obronnej przestrzeni fazowej, określone są dwie funkcje różniczkowalne: f(q

i

,p

i

,t) i

g(q

i

,p

i

,t).

Nawiasy Poissona dla tych funkcji mogą być zdefiniowane jako:

{ , } =

−