
Centralna Komisja Egzaminacyjna
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu.
WPISUJE ZDAJĄCY
KOD PESEL
Miejsce
na naklejkę
z kodem
Uk
ład gr
af
iczny © CKE
2010
EGZAMIN MATURALNY
Z MATEMATYKI
POZIOM PODSTAWOWY
1. Sprawdź, czy arkusz egzaminacyjny zawiera 20 stron
(zadania 1–33). Ewentualny brak zgłoś przewodniczącemu
zespołu nadzorującego egzamin.
2. Rozwiązania zadań i odpowiedzi wpisuj w miejscu na to
przeznaczonym.
3. Odpowiedzi do zadań zamkniętych (1–23) przenieś
na kartę odpowiedzi, zaznaczając je w części karty
przeznaczonej dla zdającego. Zamaluj pola do tego
przeznaczone. Błędne zaznaczenie otocz kółkiem
i zaznacz właściwe.
4. Pamiętaj, że pominięcie argumentacji lub istotnych
obliczeń w rozwiązaniu zadania otwartego (24–33) może
spowodować, że za to rozwiązanie nie będziesz mógł
dostać pełnej liczby punktów.
5. Pisz czytelnie i używaj tylko długopisu lub pióra
z czarnym tuszem lub atramentem.
6. Nie używaj korektora, a błędne zapisy wyraźnie przekreśl.
7. Pamiętaj, że zapisy w brudnopisie nie będą oceniane.
8. Możesz korzystać z zestawu wzorów matematycznych,
cyrkla i linijki oraz kalkulatora.
9. Na karcie odpowiedzi wpisz swój numer PESEL i przyklej
naklejkę z kodem.
10. Nie wpisuj żadnych znaków w części przeznaczonej dla
egzaminatora.
MAJ 2011
Czas pracy:
170 minut
Liczba punktów
do uzyskania: 50
MMA-P1_1P-112
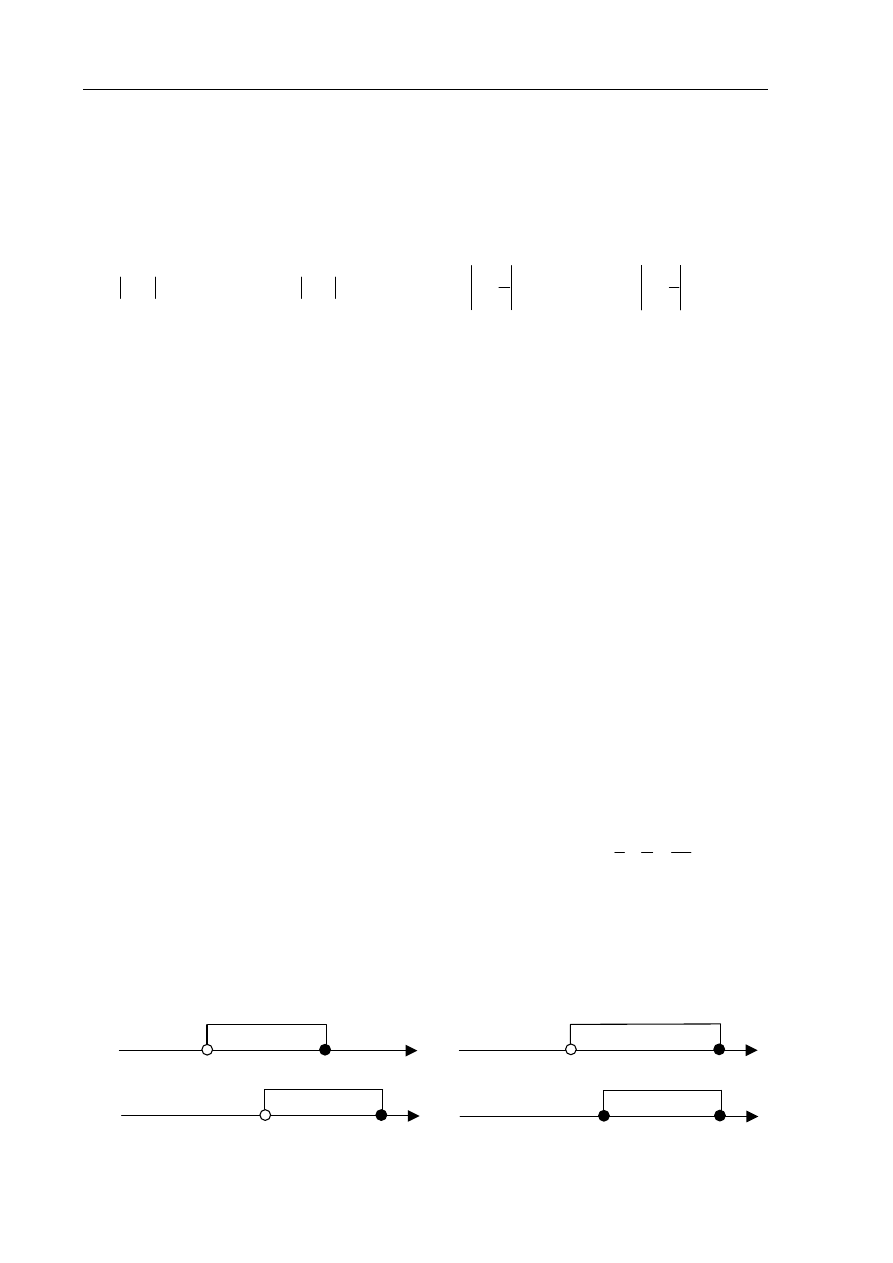
Egzamin maturalny z matematyki
Poziom podstawowy
2
ZADANIA ZAMKNIĘTE
W zadaniach od 1. do 23. wybierz i zaznacz na karcie odpowiedzi poprawną odpowiedź.
Zadanie 1. (1 pkt)
Wskaż nierówność, którą spełnia liczba
π .
A.
5
1
>
+
x
B.
1 2
x
− <
C.
2
4
3
x
+ ≤ D. 3
3
1 ≥
−
x
Zadanie 2. (1 pkt)
Pierwsza rata, która stanowi
%
9
ceny roweru, jest równa
189
zł. Rower kosztuje
A.
1701
zł.
B.
2100
zł. C.
1890
zł.
D.
2091
zł.
Zadanie 3. (1 pkt)
Wyrażenie
a
ab
a
15
10
5
2
+
−
jest równe iloczynowi
A.
(
)
3
10
1
5
2
+
− b
a
B.
(
)
3
2
5
+
− b
a
a
C.
(
)
15
10
5
+
− b
a
a
D.
(
)
3
2
5
+
− b
a
Zadanie 4. (1 pkt)
Układ równań
4
2
10
6
15
x
y
x ay
+
=
⎧
⎨ + =
⎩
ma nieskończenie wiele rozwiązań, jeśli
A.
1
a
= −
B.
0
a
=
C.
2
a
=
D.
3
a
=
Zadanie 5. (1 pkt)
Rozwiązanie równania
(
)
(
)
4
49
3
−
=
−
+
x
x
x
x
należy do przedziału
A.
(
)
,3
−∞
B.
(
)
10,
+∞
C.
(
)
1
,
5
−
−
D.
)
,
2
(
+∞
Zadanie
6.
(1 pkt)
Najmniejszą liczbą całkowitą należącą do zbioru rozwiązań nierówności
3
5
8 6 12
x
x
+ <
jest
A.
1
B.
2 C.
1
− D.
2
−
Zadanie 7. (1 pkt)
Wskaż, który zbiór przedstawiony na osi liczbowej jest zbiorem liczb spełniających
jednocześnie następujące nierówności:
(
)(
)
3
1
5
0
x
x
−
− ≤
i
1
x
>
.
A.
B.
C.
D.
1
−
3
x
1
5
x
1
6
x
1
5
x

Egzamin maturalny z matematyki
Poziom podstawowy
3
BRUDNOPIS
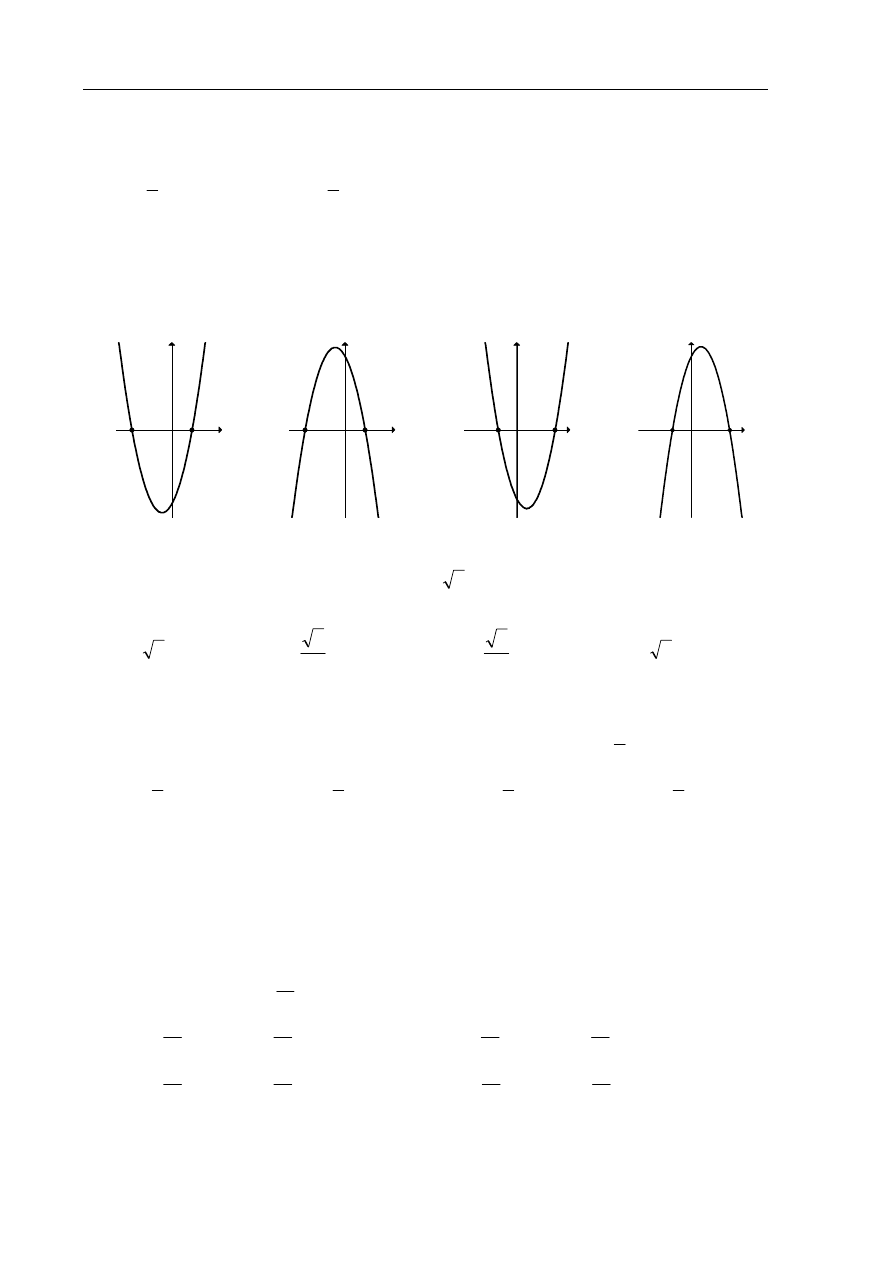
Egzamin maturalny z matematyki
Poziom podstawowy
4
Zadanie 8. (1 pkt)
Wyrażenie
)
1
2
(
log
4
−
x
jest określone dla wszystkich liczb x spełniających warunek
A.
1
2
x
≤
B.
1
2
x
> C.
0
x
≤
D.
0
x
>
Zadanie 9. (1 pkt)
Dane są funkcje liniowe
2
)
(
−
= x
x
f
oraz
4
)
(
+
= x
x
g
określone dla wszystkich liczb
rzeczywistych
x
. Wskaż, który z poniższych wykresów jest wykresem funkcji
( ) ( )
x
g
x
f
x
h
⋅
=
)
(
.
A.
x
y
-4
2
B.
x
y
-4
2
C.
x
y
-2
4
D.
x
-2
4
y
Zadanie 10 (1 pkt)
Funkcja liniowa określona jest wzorem
4
2
)
(
+
−
=
x
x
f
. Miejscem zerowym tej funkcji jest
liczba
A.
2
2
−
B.
2
2
C.
2
2
−
D.
2
2
Zadanie 11. (1 pkt)
Dany jest nieskończony ciąg geometryczny
( )
n
a , w którym
3
1
a
= i
4
2
3
a
= . Wtedy
A.
1
2
3
a
=
B.
1
4
9
a
= C.
1
3
2
a
= D.
1
9
4
a
=
Zadanie 12. (1 pkt)
Dany jest nieskończony rosnący ciąg arytmetyczny
( )
n
a o wyrazach dodatnich. Wtedy
A.
10
7
4
a
a
a
=
+
B.
8
3
6
4
a
a
a
a
+
=
+
C.
8
3
9
2
a
a
a
a
+
=
+
D.
8
7
5
2a
a
a
=
+
Zadanie 13. (1 pkt)
Kąt
α jest ostry i
5
cos
13
α
=
. Wtedy
A.
12
sin
13
α
=
oraz
12
tg
5
α
=
B.
12
sin
13
α
=
oraz
5
tg
12
α
=
C.
12
sin
5
α
=
oraz
12
tg
13
α
=
D.
5
sin
12
α
=
oraz
12
tg
13
α
=

Egzamin maturalny z matematyki
Poziom podstawowy
5
BRUDNOPIS
Egzamin maturalny z matematyki
Poziom podstawowy
6
Zadanie 14. (1 pkt)
Wartość wyrażenia
2
2
2
2
sin 38
cos 38
1
sin 52
cos 52
1
° +
° −
° +
° +
jest równa
A.
1
2
B.
0
C.
1
2
−
D.
1
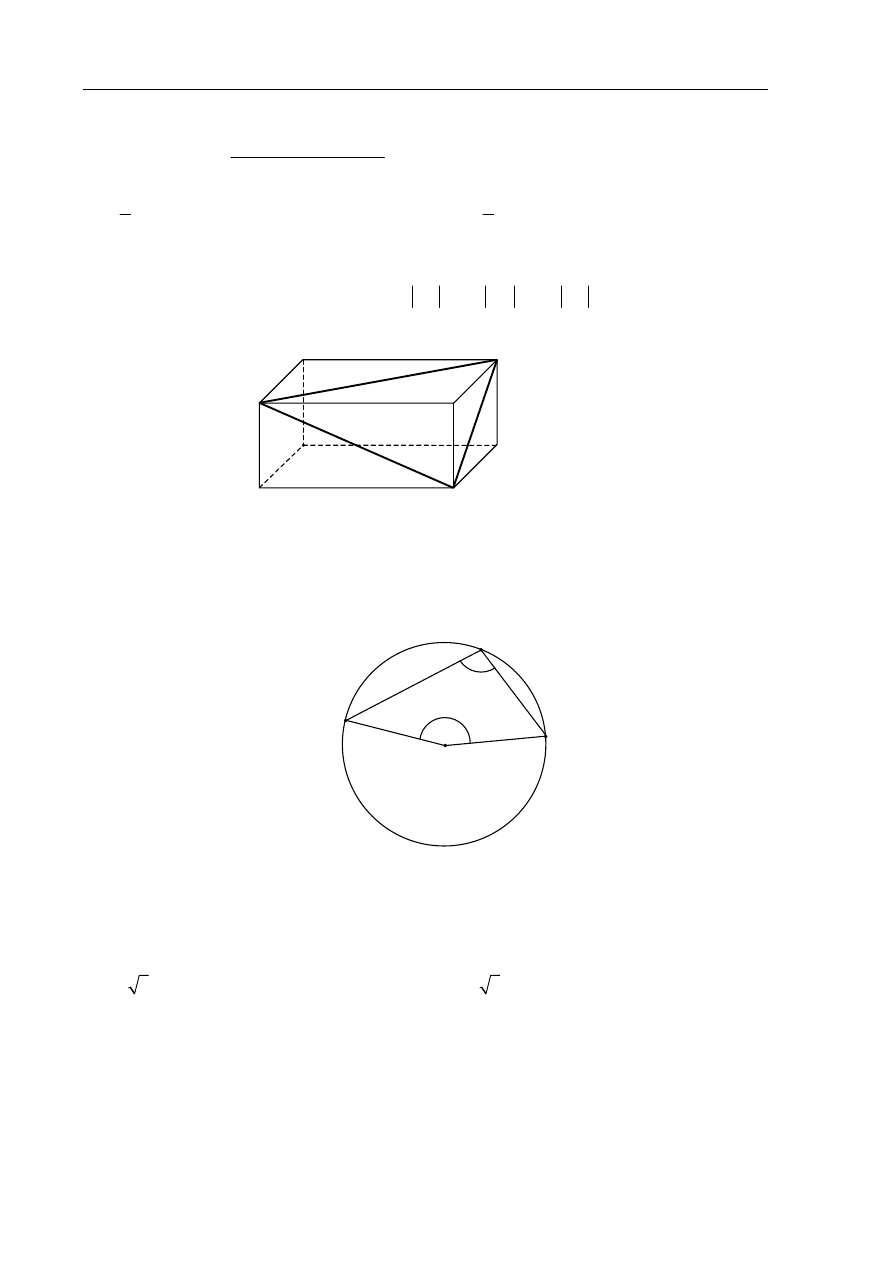
Zadanie 15. (1 pkt)
W prostopadłościanie ABCDEFGH mamy:
5
=
AB
,
4
=
AD
,
3
=
AE
. Który z odcinków
AB, BG, GE, EB jest najdłuższy?
A.
AB
B.
BG
C.
GE
D.
EB
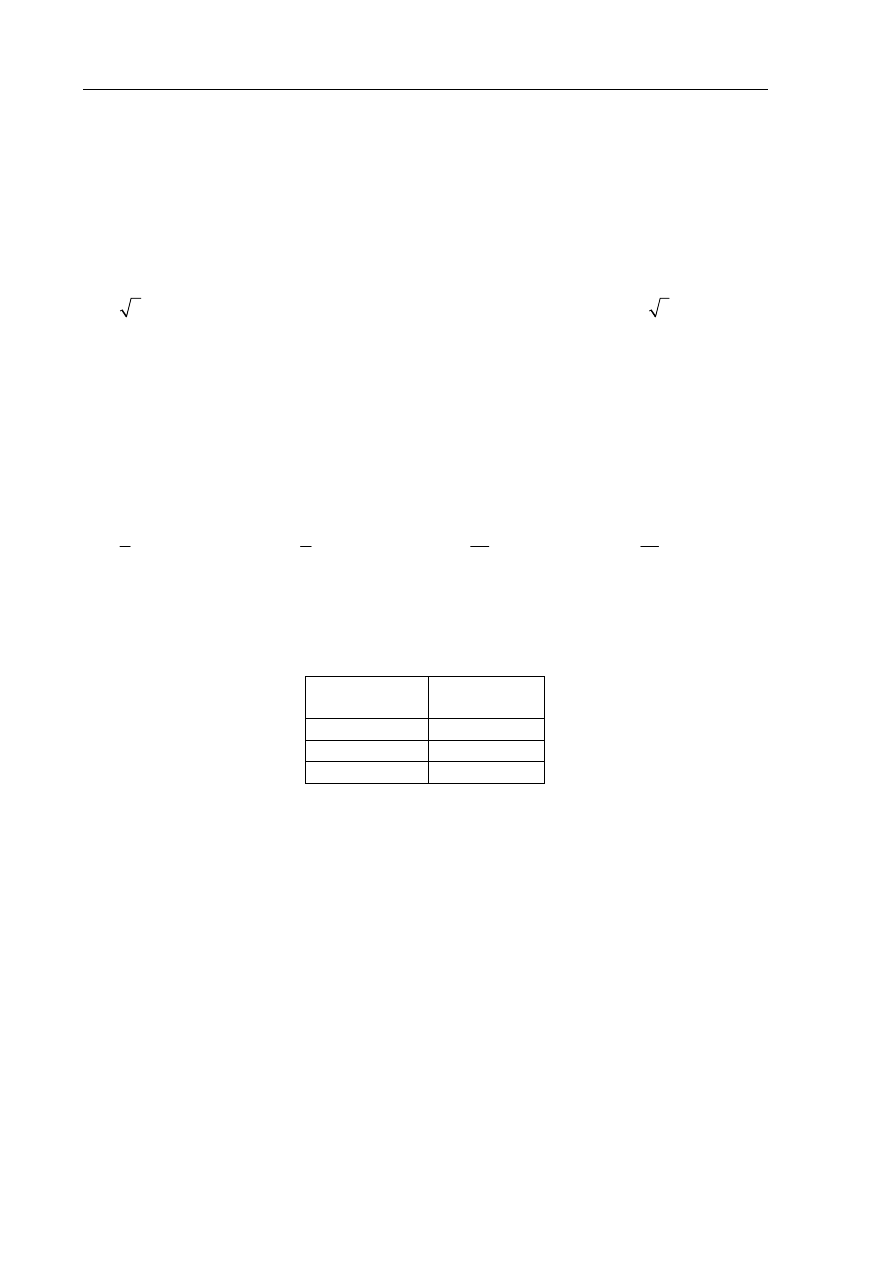
Zadanie 16. (1 pkt)
Punkt O jest środkiem okręgu. Kąt wpisany
α ma miarę
A.
°
80
B.
°
100
C.
110
°
D.
120
°
Zadanie 17. (1 pkt)
Wysokość rombu o boku długości 6 i kącie ostrym
60
°
jest równa
A.
3 3
B.
3
C.
6 3 D.
6
Zadanie 18. (1 pkt)
Prosta k ma równanie
2
3
y
x
=
− . Wskaż równanie prostej l równoległej do prostej k
i przechodzącej przez punkt D o współrzędnych
(
)
2,1
−
.
A.
2
3
y
x
= − +
B.
2
1
y
x
=
+ C.
2
5
y
x
=
+ D. 1
y
x
= − +
H
G
F
E
D
A
B
C
A
O
B
C
α
160º

Egzamin maturalny z matematyki
Poziom podstawowy
7
BRUDNOPIS
Egzamin maturalny z matematyki
Poziom podstawowy
8
Zadanie 19. (1 pkt)
Styczną do okręgu
(
)
2
2
1
4 0
x
y
−
+
− =
jest prosta o równaniu
A.
1
x
=
B.
3
x
=
C.
0
y
=
D.
4
y
=
Zadanie 20. (1 pkt)
Pole powierzchni całkowitej sześcianu jest równe 54. Długość przekątnej tego sześcianu jest
równa
A.
6
B.
3
C.
9
D.
3 3
Zadanie 21. (1 pkt)
Objętość stożka o wysokości 8 i średnicy podstawy 12 jest równa
A.
124
π
B.
96
π
C.
64
π
D.
32
π
Zadanie
22. (1 pkt)
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania
sumy oczek równej trzy wynosi
A.
1
6
B.
1
9
C.
1
12
D.
1
18
Zadanie 23. (1 pkt)
Uczniowie pewnej klasy zostali poproszeni o odpowiedź na pytanie: „Ile osób liczy twoja
rodzina?” Wyniki przedstawiono w tabeli:
Liczba osób
w rodzinie
liczba
uczniów
3 6
4 12
x
2
Średnia liczba osób w rodzinie dla uczniów tej klasy jest równa 4. Wtedy liczba x jest równa
A.
3
B.
4
C.
5
D.
7

Egzamin maturalny z matematyki
Poziom podstawowy
9
BRUDNOPIS

Egzamin maturalny z matematyki
Poziom podstawowy
10
ZADANIA OTWARTE
Rozwiązania zadań o numerach od 24. do 33. należy zapisać w wyznaczonych miejscach
pod treścią zadania.
Zadanie 24. (2 pkt)
Rozwiąż nierówność
0
3
10
3
2
≤
+
− x
x
.
Odpowiedź: ................................................................................................................................ .
Zadanie 25. (2 pkt)
Uzasadnij, że jeżeli
1
=
+ b
a
i
7
2
2
=
+ b
a
, to
4
4
31
a
b
+
=
.
Egzamin maturalny z matematyki
Poziom podstawowy
11
Zadanie
26. (2 pkt)
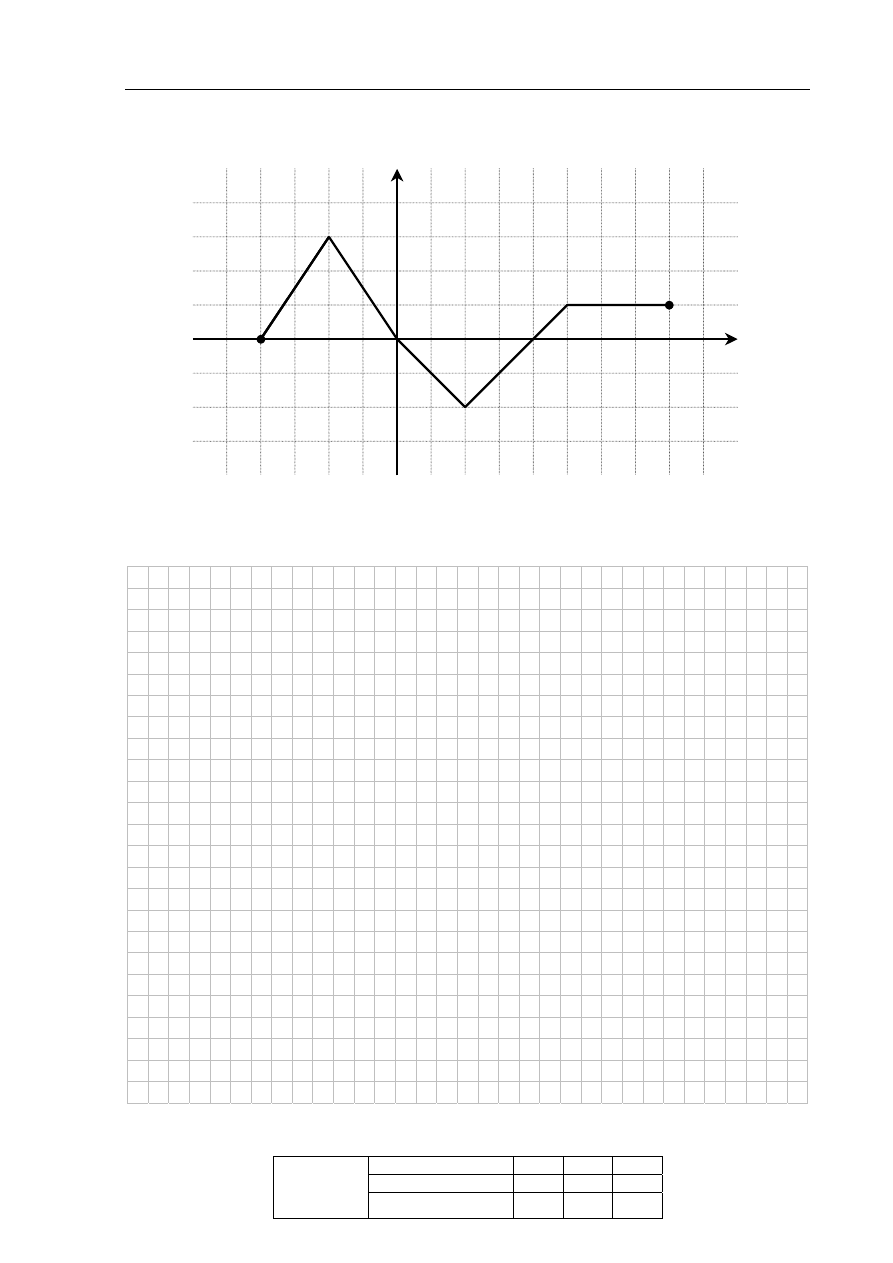
Na rysunku przedstawiono wykres funkcji f.
Odczytaj z wykresu i zapisz:
a) zbiór wartości funkcji f,
b) przedział maksymalnej długości, w którym funkcja f jest malejąca.
Odpowiedź: ................................................................................................................................ .
Nr zadania
24.
25.
26.
Maks.
liczba
pkt 2 2 2
Wypełnia
egzaminator
Uzyskana liczba pkt
y
x
0
1
2
3
4
1
2
3
–1
–2
–3
–4
–3
–2
–1
–5
4
5
6
7
8
9

Egzamin maturalny z matematyki
Poziom podstawowy
12
Zadanie 27. (2 pkt)
Liczby , , 19
x y
w podanej kolejności tworzą ciąg arytmetyczny, przy czym
8
x y
+ = .
Oblicz x i y.
Odpowiedź: ................................................................................................................................ .
Zadanie
28.
(2 pkt)
Kąt
α jest ostry i sin
cos
2
cos
sin
α
α
α
α
+
= . Oblicz wartość wyrażenia
α
α
cos
sin
⋅
.
Odpowiedź: ................................................................................................................................ .

Egzamin maturalny z matematyki
Poziom podstawowy
13
Zadanie 29. (2 pkt)
Dany jest czworokąt ABCD, w którym
CD
AB ||
. Na boku BC wybrano taki punkt E,
że
EC
CD
=
i
EB
BA
=
. Wykaż, że kąt AED jest prosty.
Odpowiedź: ................................................................................................................................ .
Nr zadania
27.
28.
29.
Maks.
liczba
pkt 2 2 2
Wypełnia
egzaminator
Uzyskana liczba pkt

Egzamin maturalny z matematyki
Poziom podstawowy
14
Zadanie
30. (2 pkt)
Ze zbioru liczb
}
7
,...,
3
,
2
,
1
{
losujemy kolejno dwa razy po jednej liczbie ze zwracaniem.
Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 3.
Odpowiedź: ................................................................................................................................ .

Egzamin maturalny z matematyki
Poziom podstawowy
15
Zadanie 31. (4 pkt)
Okrąg o środku w punkcie
)
7
,
3
(
=
S
jest styczny do prostej o równaniu
.
3
2
−
= x
y
Oblicz
współrzędne punktu styczności.
Odpowiedź: ................................................................................................................................ .
Nr zadania
30.
31.
Maks. liczba pkt
2
4
Wypełnia
egzaminator
Uzyskana liczba pkt

Egzamin maturalny z matematyki
Poziom podstawowy
16
Zadanie 32. (5 pkt)
Pewien turysta pokonał trasę 112 km, przechodząc każdego dnia tę samą liczbę kilometrów.
Gdyby mógł przeznaczyć na tę wędrówkę o 3 dni więcej, to w ciągu każdego dnia mógłby
przechodzić o 12 km mniej. Oblicz, ile kilometrów dziennie przechodził ten turysta.

Egzamin maturalny z matematyki
Poziom podstawowy
17
Odpowiedź: ................................................................................................................................ .
Nr zadania
32.
Maks. liczba pkt
5
Wypełnia
egzaminator
Uzyskana liczba pkt
Egzamin maturalny z matematyki
Poziom podstawowy
18
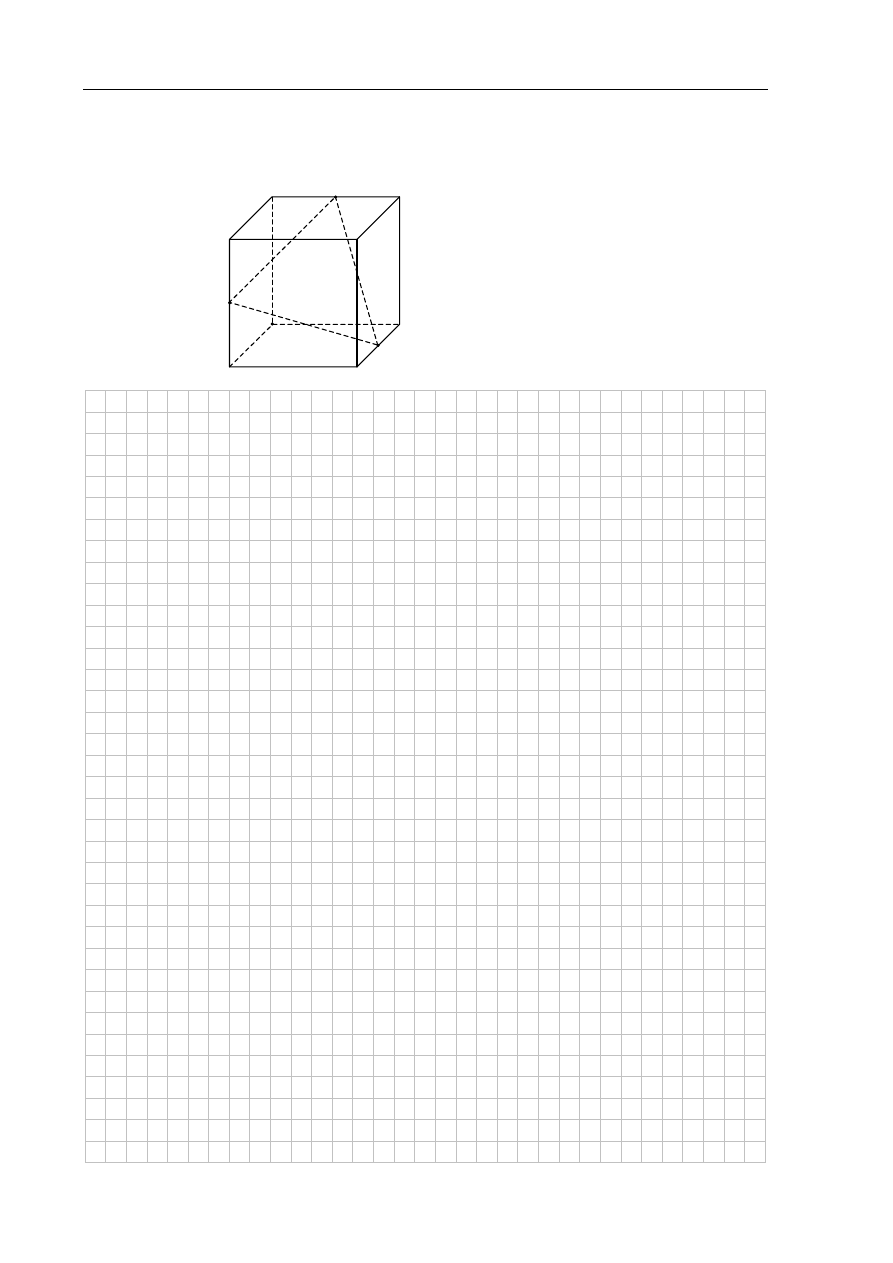
Zadanie 33. (4 pkt)
Punkty K, L i M są środkami krawędzi BC, GH i AE sześcianu ABCDEFGH o krawędzi
długości 1 (zobacz rysunek). Oblicz pole trójkąta KLM.
L
H
G
F
E
M
K
D
A
B
C

Egzamin maturalny z matematyki
Poziom podstawowy
19
Odpowiedź: ................................................................................................................................ .
Nr zadania
33.
Maks. liczba pkt
4
Wypełnia
egzaminator
Uzyskana liczba pkt

Egzamin maturalny z matematyki
Poziom podstawowy
20
BRUDNOPIS
MMA-P1_1P-112
32
33
27
28
29
30
31
26
25
24
Nr
zad.
Punkty
0
1
2
3
4
5
WYPE£NIA EGZAMINATOR
WYPE£NIA ZDAJ¥CY
SUMA
PUNKTÓW
D
J
0
0
1
1
2
2
3
3
4
4
5
5
6
6
7
7
8
8
9
9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Odpowiedzi
Nr
zad.
PESEL
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
B
B
B
B
B
B
B
B
B
B
B
B
B
B
B
B
B
B
B
B
B
B
B
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
D
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
Miejsce na naklejkê
z nr PESEL

KOD EGZAMINATORA
Czytelny podpis egzaminatora
KOD ZDAJ¥CEGO

Centralna Komisja Egzaminacyjna w Warszawie
EGZAMIN MATURALNY 2011
MATEMATYKA
POZIOM PODSTAWOWY
Kryteria oceniania odpowiedzi
MAJ 2011

Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
2
Zadanie 1. (0–1)
Obszar standardów
Opis wymagań
Poprawna
odpowiedź
(1 p.)
Wykorzystanie i tworzenie
informacji
Wykorzystanie pojęcia wartości
bezwzględnej
C
Zadanie 2. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Wykonanie obliczeń procentowych
B
Zadanie 3. (0–1)
Wykorzystanie i tworzenie
informacji
Rozłożenie wielomianu na czynniki
z zastosowaniem wyłączenia wspólnego
czynnika poza nawias
B
Zadanie 4. (0–1)
Modelowanie matematyczne Rozwiązanie układu równań
D
Zadanie 5. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Rozwiązanie równania liniowego
i sprawdzenie czy rozwiązanie należy
do danego przedziału
D
Zadanie 6. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Sprawdzenie, które z podanych liczb
spełniają nierówność i wybranie z nich
najmniejszej
B
Zadanie 7. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Zinterpretowanie rozwiązania
nierówności kwadratowej i liniowej na osi
liczbowej
C
Zadanie 8. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Wykorzystanie definicji logarytmu
B
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
3
Zadanie 9. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Określenie funkcji za pomocą wzoru
i interpretowanie wykresów funkcji
kwadratowych
A
Zadanie 10. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Obliczenie miejsca zerowego funkcji
liniowej
D
Zadanie 11. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Zastosowanie wzory na n-ty wyraz ciągu
geometrycznego
D
Zadanie 12. (0–1)
Użycie i tworzenie strategii
Zastosowanie wzoru na n-ty wyraz ciągu
arytmetycznego
C
Zadanie 13. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Wyznaczenie wartości pozostałych
funkcji tego samego kąta ostrego, gdy
dana jest wartość jednej z nich
A
Zadanie 14. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Zastosowanie prostych związków między
funkcjami trygonometrycznymi kąta
ostrego
B
Zadanie 15. (0–1)
Użycie i tworzenie strategii
Znalezienie związków miarowych
w przestrzeni
C
Zadanie 16. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Skorzystanie ze związków między kątem
środkowym i kątem wpisanym
B
Zadanie 17. (0–1)
Użycie i tworzenie strategii
Znalezienie związków miarowych
w figurach płaskich
A

Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
4
Zadanie 18. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Zbadanie równoległości i prostopadłości
prostych na podstawie ich równań
kierunkowych
C
Zadanie 19. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Posłużenie się równaniem okręgu
(
) (
)
2
2
2
r
b
y
a
x
=
−
+
−
i sprawdzanie
czy dana prosta jest styczną
B
Zadanie 20. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Wyznaczenie związków miarowych
w sześcianie
D
Zadanie 21. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Wyznaczenie związków miarowych
w bryłach obrotowych
B
Zadanie 22. (0–1)
Modelowanie matematyczne
Zastosowanie twierdzenia znanego jako
klasyczna definicja prawdopodobieństwa
do obliczenia prawdopodobieństwa
zdarzenia
D
Zadanie 23. (0–1)
Wykorzystanie
i interpretowanie reprezentacji
Obliczenie średniej arytmetycznej
D

Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
5
Zadanie 24. (0–2)
Rozwiązanie
Rozwiązanie nierówności kwadratowej składa się z dwóch etapów.
Pierwszy etap może być realizowany na 2 sposoby:
I sposób rozwiązania (realizacja pierwszego etapu)
Znajdujemy pierwiastki trójmianu kwadratowego
2
3
10
3
x
x
−
+
• obliczamy wyróżnik tego trójmianu:
100 4 3 3 64
Δ =
− ⋅ ⋅ =
i stąd
1
10 8 1
6
3
x
−
=
= oraz
2
10 8
3
6
x
+
=
=
albo
• stosujemy wzory Viète’a:
1
2
10
3
x
x
+
=
oraz
1
2
1
x x
⋅
=
i stąd
1
1
3
x
= oraz
2
3
x
=
albo
• podajemy je bezpośrednio, np. zapisując pierwiastki trójmianu lub postać iloczynową
trójmianu, lub zaznaczając na wykresie
1
1
3
x
= ,
2
3
x
= lub
(
)
1
3
3
3
x
x
⎛
⎞
−
−
⎜
⎟
⎝
⎠
lub
II sposób rozwiązania
(realizacja pierwszego etapu)
Wyznaczamy postać kanoniczną trójmianu kwadratowego
2
3
10
3
x
x
−
+ i zapisujemy
nierówność w postaci, np.
2
10
64
3
0 ,
6
12
x
⎛
⎞
−
−
≤
⎜
⎟
⎝
⎠
stąd
2
10
64
3
0
6
36
x
⎡
⎤
⎛
⎞
−
−
≤
⎢
⎥
⎜
⎟
⎝
⎠
⎢
⎥
⎣
⎦
a następnie
Wykorzystanie
i interpretowanie reprezentacji
Rozwiązanie nierówności kwadratowej
– 4 –
3
–
2
–1
1
2
3
4
5
–2
–1
1
2
3
4
5
x
y
6
–3
6
0
1
3

Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
6
• przekształcamy nierówność, tak by jej lewa strona była zapisana w postaci
iloczynowej
10 8
10 8
3
0
6
6
6
6
x
x
⎛
⎞ ⎛
⎞
−
−
⋅
−
+
≤
⎜
⎟ ⎜
⎟
⎝
⎠ ⎝
⎠
(
)
1
3
3
3
0
x
x
⎛
⎞ ≤
⎜
⎟
⎝
⎠
− ⋅ −
albo
• przekształcamy nierówność do postaci równoważnej, korzystając z własności wartości
bezwzględnej
2
10
64
6
36
x
⎛
⎞
−
≤
⎜
⎟
⎝
⎠
10
8
6
6
x
−
≤
Drugi etap rozwiązania:
Podajemy zbiór rozwiązań nierówności:
1
3
3
x
≤ ≤
lub
1
, 3
3
lub
1
, 3
3
x
∈
.
Schemat oceniania
Zdający otrzymuje ............................................................................................................1 pkt
gdy:
• zrealizuje pierwszy etap rozwiązania i na tym poprzestanie lub błędnie zapisze zbiór
rozwiązań nierówności, np.
o
obliczy lub poda pierwiastki trójmianu kwadratowego
1
3
x
= ,
3
x
=
i na tym
poprzestanie lub błędnie zapisze zbiór rozwiązań nierówności
o
zaznaczy na wykresie miejsca zerowe funkcji
( )
2
3
10
3
f x
x
x
=
−
+
i na tym
poprzestanie lub błędnie zapisze zbiór rozwiązań nierówności
o
rozłoży trójmian kwadratowy na czynniki liniowe, np.
(
)
1
3
3
3
x
x
⎛
⎞
−
⋅ −
⎜
⎟
⎝
⎠
i na
tym poprzestanie lub błędnie rozwiąże nierówność
o
zapisze nierówność
10
8
6
6
x
−
≤
i na tym poprzestanie lub błędnie zapisze
zbiór rozwiązań nierówności
albo
• realizując pierwszy etap, popełni błąd (ale otrzyma dwa różne pierwiastki)
i konsekwentnie do tego rozwiąże nierówność, np.
o
popełni błąd rachunkowy przy obliczaniu wyróżnika lub pierwiastków
trójmianu kwadratowego i konsekwentnie do popełnionego błędu rozwiąże
nierówność
o
błędnie zapisze równania wynikające ze wzorów Viète’a, np.:
1
2
10
3
x
x
+
= −
i
1
2
1
x x
⋅
=
lub
1
2
10
3
x
x
+
=
i
1
2
1
x x
⋅
= −
i konsekwentnie do popełnionego
błędu rozwiąże nierówność
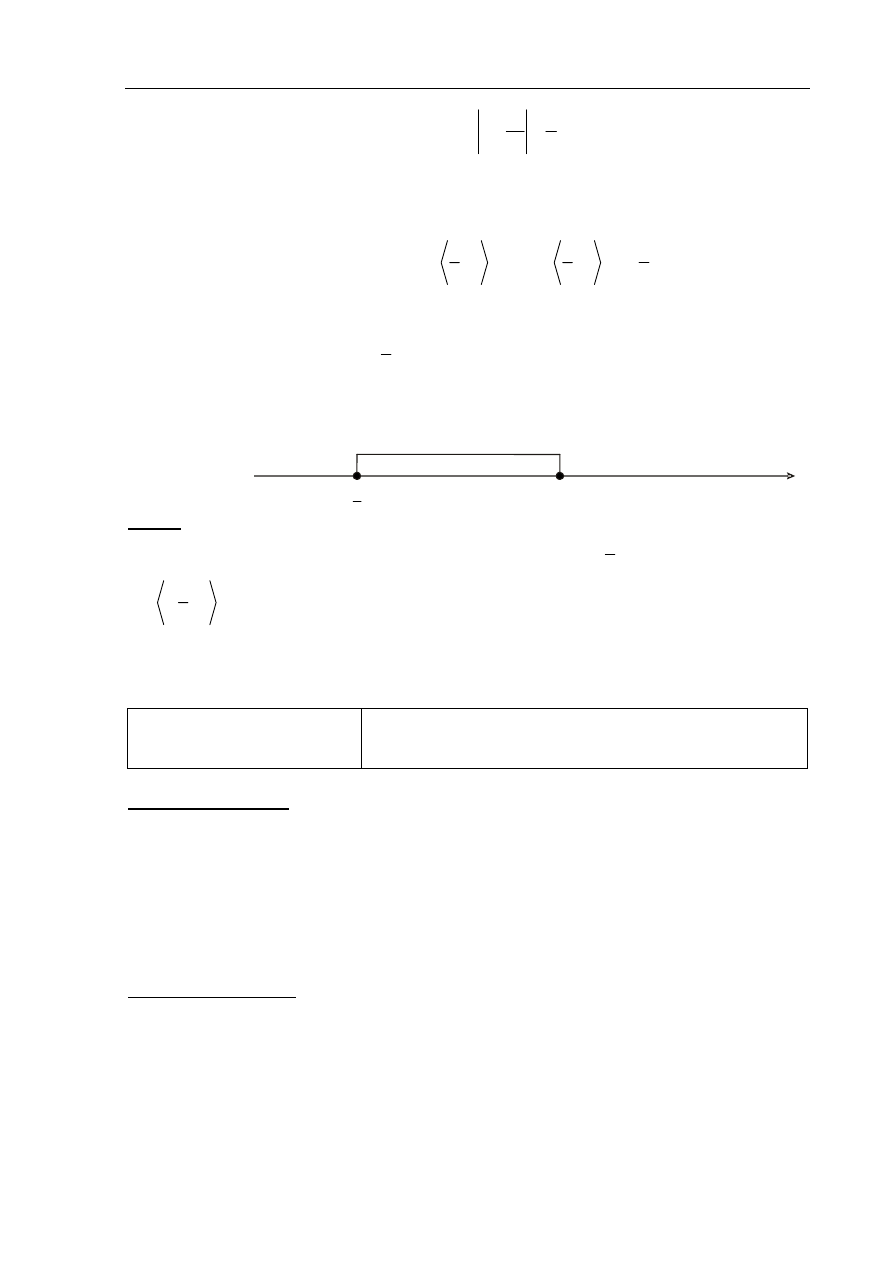
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
7
o
błędnie zapisze nierówność, np.
10
8
6
6
x
+
≤
i konsekwentnie do popełnionego
błędu rozwiąże nierówność.
Zdający otrzymuje ............................................................................................................ 2 pkt
gdy:
• poda zbiór rozwiązań nierówności:
1
, 3
3
lub
1
, 3
3
x
∈
lub
1
3
3
x
≤ ≤ ,
albo
• sporządzi ilustrację geometryczną (oś liczbowa, wykres) i zapisze zbiór rozwiązań
nierówności w postaci:
1
3
x
≥ ,
3
x
≤
albo
• poda zbiór rozwiązań nierówności w postaci graficznej z poprawnie zaznaczonymi
końcami przedziałów
Uwaga
Jeżeli zdający poprawnie obliczy pierwiastki trójmianu
1
1
3
x
= i
2
3
x
=
i zapisze np.
1
, 3
3
x
∈ −
, popełniając tym samym błąd przy przepisywaniu jednego z pierwiastków, to za
takie rozwiązanie otrzymuje 2 punkty.
Zadania 25. (0–2)
I sposób rozwiązania
Ponieważ
1
a b
+ =
, więc
(
)
2
1
a b
+
= , czyli
2
2
2
1
a
ab b
+
+
= .
Ponieważ
2
2
7
a
b
+
= , więc
2
7 1
ab
+ =
. Stąd mamy, że
3
ab
= −
i
( )
2
2 2
9
a b
ab
=
= .
Stosując wzory skróconego mnożenia, zapisujemy wyrażenie
4
4
31
a
b
+
=
w postaci:
(
)
2
2
2
2 2
2
31
a
b
a b
+
−
=
czyli
2
7
2 9 31
− ⋅ =
co należało uzasadnić.
II sposób rozwiązania
Przekształcamy tezę w sposób równoważny:
4
4
31
a
b
+
=
(
)
2
2
2
2 2
2
31
a
b
a b
+
−
=
2 2
49 2
31
a b
−
=
2 2
9
a b
= .
Rozumowanie i argumentacja Uzasadnienie zależności arytmetycznej z zastosowaniem
wzorów skróconego mnożenia
3
x
1
3

Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
8
Korzystając z założeń
2
2
7
a
b
+
= i
1
a b
+ =
, otrzymujemy
2
7 1
ab
+ =
.
Stąd
3
ab
= −
. Zatem
2 2
9
a b
= , co kończy dowód.
Schemat oceniania I i II sposobu rozwiązania
Zdający otrzymuje .............................................................................................................1 pkt
gdy:
• korzystając z założeń obliczy, że
3
ab
= −
i na tym poprzestanie lub dalej popełnia
błędy
albo
• przekształci tezę w sposób równoważny do postaci
2 2
9
a b
= i na tym poprzestanie lub
dalej popełnia błędy
Zdający otrzymuje .............................................................................................................2 pkt
gdy przeprowadzi pełne rozumowanie.
III sposób rozwiązania
Tak jak w sposobie I obliczamy, że
3
ab
= −
.
Korzystamy ze wzoru dwumianowego Newtona:
(
)
(
)
( )
( )
( )
4
2
4
3
2 2
3
4
4
2
2
4
2
4
4
4
4
4
4
4
6
4
4
6
4 3 7 6
3
84 54
30
a b
a
a b
a b
ab
b
a
ab a
b
ab
b
a
b
a
b
a
b
+
=
+
+
+
+
=
+
+
+
+
=
=
+
+ − ⋅ + ⋅ −
=
+
−
+
=
+
−
Stąd
4
4
31
a
b
+
=
.
Schemat oceniania III sposobu rozwiązania
Zdający otrzymuje .............................................................................................................1 pkt
gdy
• poda lub obliczy wartość wyrażenia
3
ab
= −
i na tym poprzestanie lub dalej popełni
błędy
albo
• wykorzysta wzór dwumianowy Newtona i zapisze np.
(
)
(
)
( )
4
2
4
2
2
4
4
6
a b
a
ab a
b
ab
b
+
=
+
+
+
+
.
Zdający otrzymuje .............................................................................................................2 pkt
gdy przeprowadzi pełne rozumowanie.
IV sposób rozwiązania
Rozwiązujemy układ równań, wyznaczając
a
i
b
:
2
2
7
1
a
b
a b
⎧ +
=
⎨
+ =
⎩
stąd:
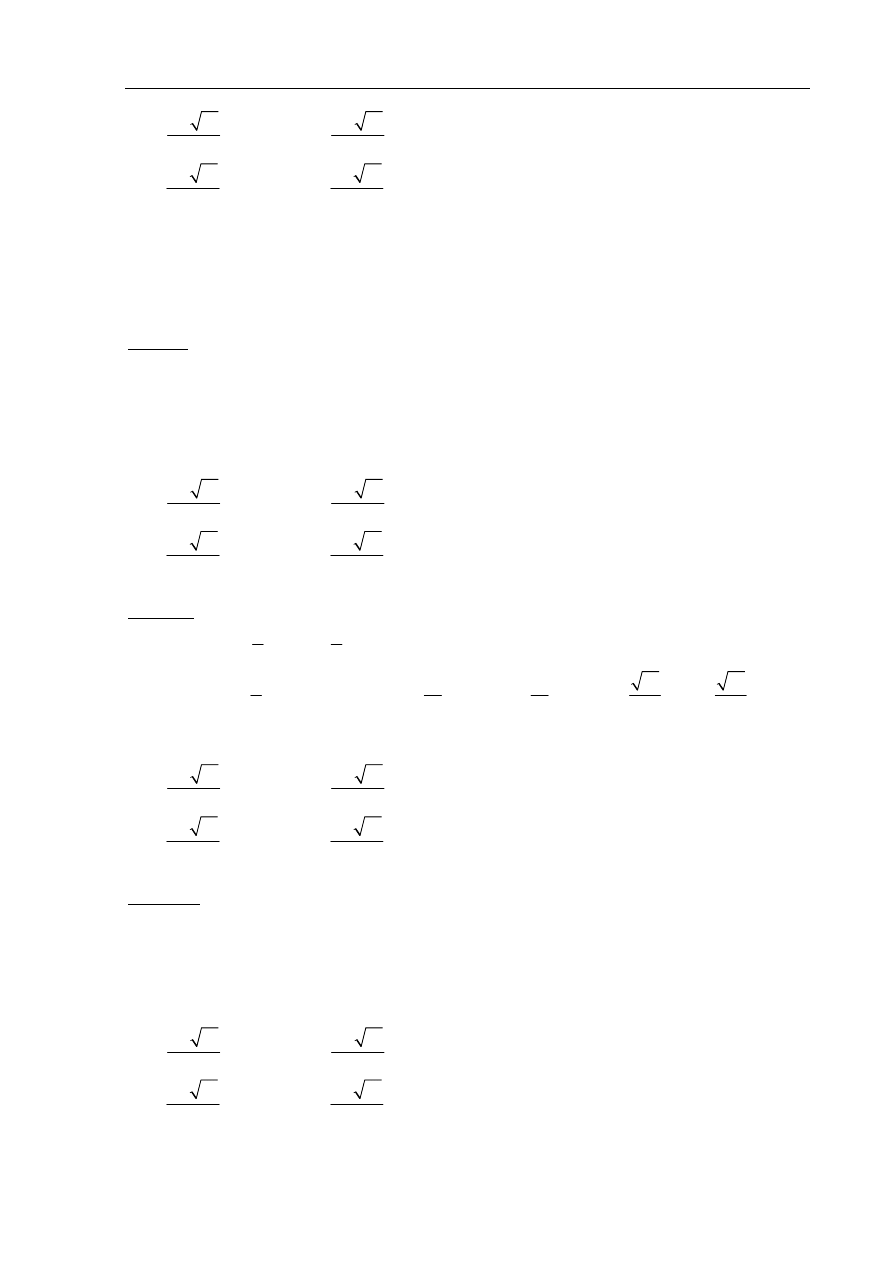
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
9
1
13
2
1
13
2
a
b
⎧
−
=
⎪⎪
⎨
+
⎪ =
⎪⎩
lub
1
13
2
1
13
2
a
b
⎧
+
=
⎪⎪
⎨
−
⎪ =
⎪⎩
Układ równań
2
2
7
1
a
b
a b
⎧ +
=
⎨
+ =
⎩
możemy rozwiązać jednym z podanych sposobów.
I sposób
Podstawiamy
1
b
a
= −
do równania
2
2
7
a
b
+
= , stąd otrzymujemy równanie
(
)
2
2
1
7
a
a
+ −
= , które jest równoważne równaniu
2
2
2
6 0
a
a
−
− = , czyli
2
3 0
a
a
− − = .
Obliczamy
13
Δ =
oraz
1
13
2
1
13
2
a
b
⎧
−
=
⎪⎪
⎨
+
⎪ =
⎪⎩
lub
1
13
2
1
13
2
a
b
⎧
+
=
⎪⎪
⎨
−
⎪ =
⎪⎩
II sposób
Oznaczamy:
1
2
a
x
= + ,
1
2
b
x
= − .
Wtedy
2
2
2
1
2
7
2
a
b
x
+
= +
= , stąd
2
13
2
2
x
=
, czyli
2
13
4
x
=
, więc
13
2
x
=
,
13
2
x
= −
.
Stąd otrzymujemy:
1
13
2
1
13
2
a
b
⎧
−
=
⎪⎪
⎨
+
⎪ =
⎪⎩
lub
1
13
2
1
13
2
a
b
⎧
+
=
⎪⎪
⎨
−
⎪ =
⎪⎩
III sposób
Obliczamy
3
ab
= −
tak jak w I sposobie rozwiązania. Mamy zatem układ równań:
1
3
a b
ab
+ =
⎧
⎨
= −
⎩
Stąd otrzymujemy:
1
13
2
1
13
2
a
b
⎧
−
=
⎪⎪
⎨
+
⎪ =
⎪⎩
lub
1
13
2
1
13
2
a
b
⎧
+
=
⎪⎪
⎨
−
⎪ =
⎪⎩
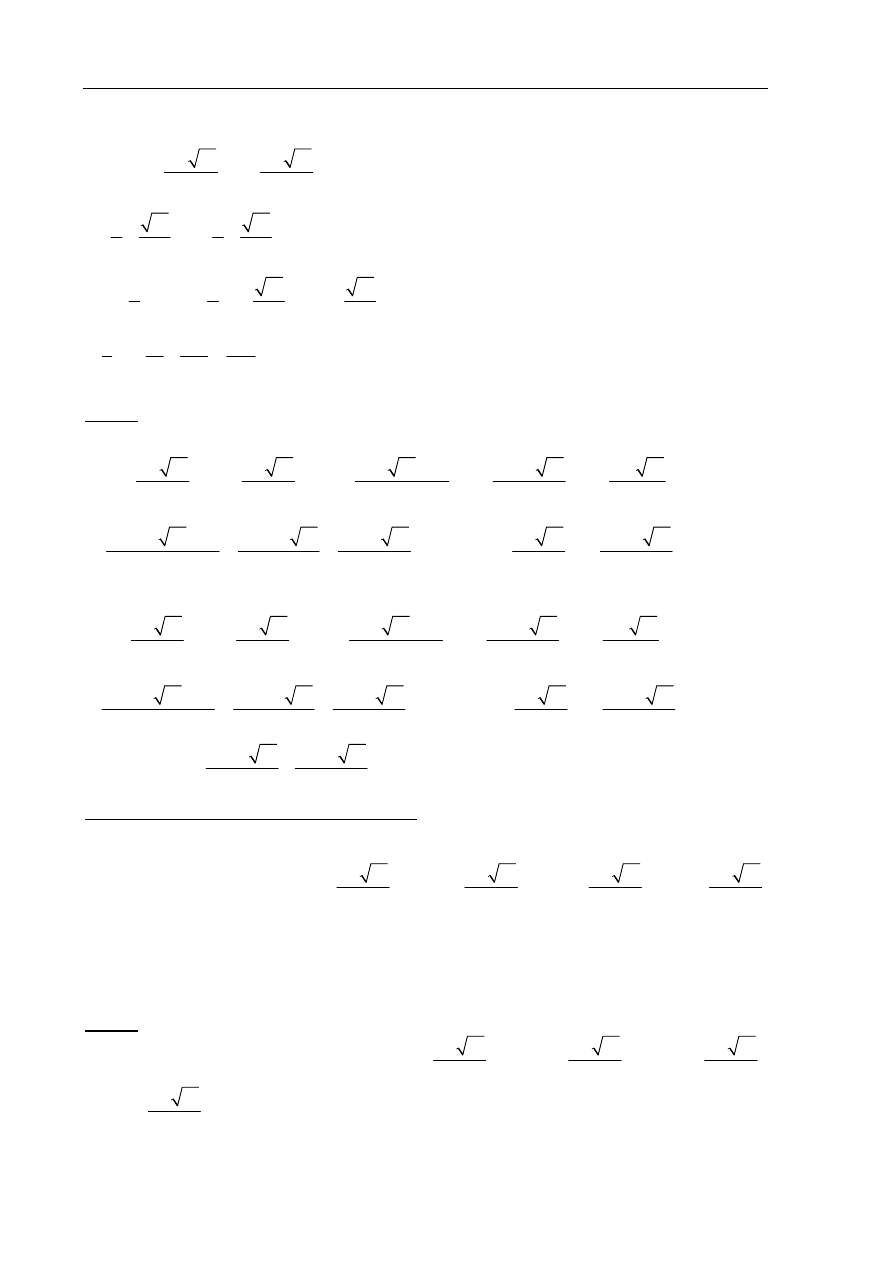
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
10
Obliczamy
4
4
a
b
+ , korzystając ze wzoru
(
) (
)
4
4
4
2
2
4
2
12
2
c
d
c
d
c
c d
d
+
+ −
=
+
+
:
4
4
4
4
4
4
2
4
4
2
1
13
1
13
2
2
1
13
1
13
2
2
2
2
1
1
13
13
2
12
2
2
2
2
2
1
13 169
248
3
31
8
4
8
8
a
b
⎛
⎞
⎛
⎞
+
−
+
=
+
=
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
⎛
⎞
⎛
⎞
=
+
+
−
=
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
⎛
⎞
⎛
⎞
⎛ ⎞
⎛ ⎞
= ⋅
+ ⋅
⋅
+ ⋅
=
⎜
⎟
⎜
⎟
⎜ ⎟
⎜ ⎟
⎝ ⎠
⎝ ⎠ ⎝
⎠
⎝
⎠
= + ⋅
+
=
=
Uwaga
Zdający może także obliczyć:
2
4
2
2
2
2
4
4
4
1
13
1
13
1 2 13 13
14 2 13
7
13
2
2
4
4
2
49 14 13 13 62 14 13
31 7 13
1
13
31 7 13
albo
4
4
2
2
2
a
a
⎛
⎞
⎛
⎞
⎛
⎞
⎛
⎞
⎛
⎞
⎛
⎞
+
+
+
+
+
+
⎜
⎟
=
=
=
=
=
=
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
⎝
⎠
⎝
⎠
⎝
⎠
⎝
⎠
⎛
⎞
+
+
+
+
−
−
=
=
=
=
=
⎜
⎟
⎜
⎟
⎝
⎠
oraz
2
4
2
2
2
2
4
4
4
1
13
1
13
1 2 13 13
14 2 13
7
13
2
2
4
4
2
49 14 13 13 62 14 13
31 7 13
1
13
31 7 13
albo
4
4
2
2
2
b
b
⎛
⎞
⎛
⎞
⎛
⎞
⎛
⎞
⎛
⎞
⎛
⎞
−
−
−
+
−
−
⎜
⎟
=
=
=
=
=
=
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
⎝
⎠
⎝
⎠
⎝
⎠
⎝
⎠
⎛
⎞
−
+
−
−
+
+
=
=
=
=
=
⎜
⎟
⎜
⎟
⎝
⎠
Zatem
4
4
31 7 13 31 7 13
31
2
2
a
b
+
−
+
=
+
=
.
Schemat oceniania IV sposobu rozwiązania
Zdający otrzymuje .............................................................................................................1 pkt
gdy obliczy jedną z wartości
1
1
13
2
a
−
=
lub
2
1
13
2
a
+
=
lub
1
1
13
2
b
+
=
lub
2
1
13
2
b
−
=
i na tym poprzestanie lub dalej popełni błędy
Zdający otrzymuje .............................................................................................................2 pkt
gdy przeprowadzi pełne rozumowanie.
Uwaga
Jeżeli zdający obliczy jedną z wartości
1
1
13
2
a
−
=
lub
2
1
13
2
a
+
=
, lub
1
1
13
2
b
+
=
,
lub
2
1
13
2
b
−
=
i uzasadni tezę tylko dla tej jednej wartości, to otrzymuje 2 punkty.
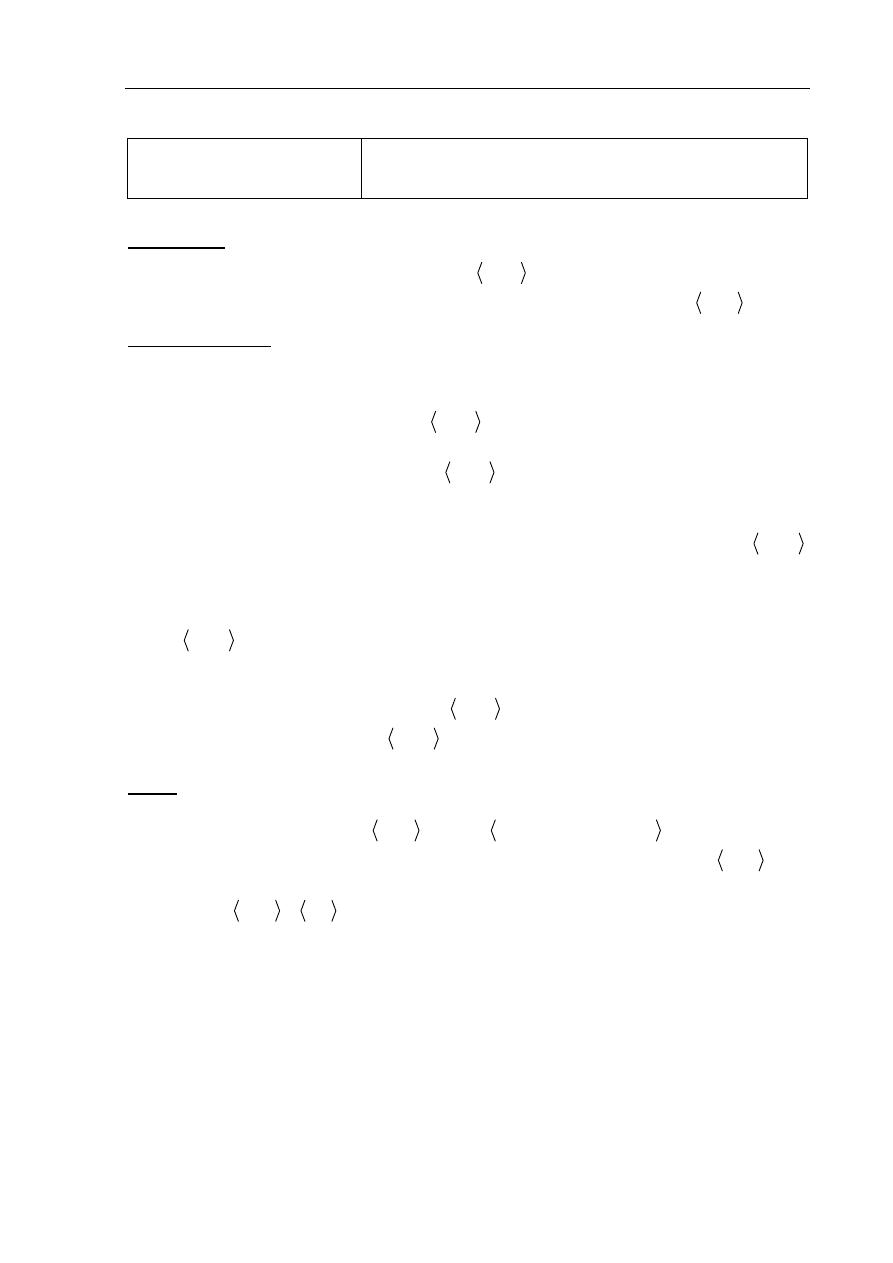
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
11
Zadanie 26. (0–2)
Rozwiązanie
Odczytujemy z wykresu zbiór wartości funkcji:
2, 3
−
.
Zapisujemy przedział maksymalnej długości,
w którym funkcja jest malejąca:
2, 2
−
.
Schemat oceniania
Zdający otrzymuje............................................................................................................. 1 pkt
gdy:
• zapisze zbiór wartości funkcji f :
2, 3
−
i na tym poprzestanie
albo
• zapisze zbiór wartości funkcji f :
2, 3
−
i błędnie zapisze przedział maksymalnej
długości, w którym ta funkcja jest malejąca
albo
• zapisze przedział maksymalnej długości, w którym funkcja f jest malejąca:
2, 2
−
i na tym poprzestanie
albo
• zapisze przedział maksymalnej długości, w którym funkcja f jest malejąca, np.:
2, 2
−
i błędnie zapisze zbiór wartości funkcji f .
Zdający otrzymuje............................................................................................................. 2 pkt
gdy zapisze zbiór wartości funkcji f :
2, 3
−
oraz przedział maksymalnej długości,
w którym funkcja f jest malejąca:
2, 2
−
.
Uwagi
1. Zdający może zapisać przedział maksymalnej długości, w którym funkcja f jest malejąca,
w postaci
2
2
x
− ≤ ≤
lub
2, 2 ,
∈ −
x
lub
)
2, 2 ,
∈ −
x
lub
(
2, 2 ,
∈ −
x
lub
(
)
2,2
x
∈ −
.
2. Zdający może zapisać zbiór wartości funkcji f, w postaci
2
3 lub
2,3 .
y
x
− ≤ ≤
∈ −
3. Zdający może zapisać przedział maksymalnej długości, w którym funkcja f jest malejąca,
w postaci
2,0
0,2
−
∪
.
4. Nie akceptujemy, jeżeli zdający zapisze przedział maksymalnej długości, w którym
funkcja f jest malejąca, w postaci
{
}
2,2
−
.
Wykorzystanie i tworzenie
informacji
Odczytanie z wykresu funkcji: zbioru wartości oraz
maksymalnego przedziału, w którym funkcja maleje

Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
12
Zadania 27. (0–2)
I sposób rozwiązania
Liczby , , 19
x y
w podanej kolejności tworzą ciąg arytmetyczny, stąd 2
19
y
x
= +
.
Zapisujemy więc układ równań
2
19
8
y
x
x
y
= +
⎧
⎨ + =
⎩
którego rozwiązaniem jest
1
x
= −
i
9
y
= .
Schemat oceniania I sposobu rozwiązania
Zdający otrzymuje .............................................................................................................1 pkt
gdy wykorzysta własności ciągu arytmetycznego i zapisze równanie np. 2
19
y
x
= +
i na tym
poprzestanie lub dalej popełnia błędy.
Zdający otrzymuje .............................................................................................................2 pkt
gdy obliczy:
1
−
=
x
i
9
=
y
.
Uwaga
Zdający może jako rozwiązanie podać ciąg
(
)
1, 9, 19
−
i wtedy również otrzymuje 2 punkty.
II sposób rozwiązania
Liczby , , 19
x y
w podanej kolejności tworzą ciąg arytmetyczny. Niech r będzie różnicą tego
ciągu i
1
x
a
= ,
2
1
y
a
a
r
=
= + ,
3
1
19
2
a
a
r
=
= +
.
Otrzymujemy układ równań
1
1
1
8
2
19
a
a
r
a
r
+ + =
⎧
⎨ + =
⎩
Rozwiązaniem tego układu jest
1
1
a
= − , 10
r
=
. Stąd:
1
1
x
a
=
= − ,
2
9
y
a
=
= .
Uwaga
Możemy również otrzymać następujące układy równań:
1
1
1
2
8
19
2
a
r
a
a
r
+ =
⎧
⎪
⎨ +
= +
⎪⎩
lub
19
2
8
y
x
r
x
r
x
y
= +
⎧
⎪ = +
⎨
⎪ + =
⎩
Schemat oceniania II sposobu rozwiązania
Zdający otrzymuje .............................................................................................................1 pkt
gdy wprowadzi oznaczenia
1
x
a
= ,
2
1
y
a
a
r
=
= + i zapisze równanie
1
2
19
a
r
+
=
i na tym
poprzestanie lub dalej popełnia błędy.
Zdający otrzymuje .............................................................................................................2 pkt
gdy obliczy:
1
−
=
x
i
9
=
y
.
Modelowanie matematyczne
Zastosowanie wzorów na n-ty wyraz ciągu arytmetycznego
lub wykorzystanie własności trzech kolejnych wyrazów
tego ciągu
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
13
III sposób rozwiązania
Wprowadzamy oznaczenia
1
x
a
= ,
2
y
a
=
,
3
19 a
= .
Obliczamy:
3
19 8 19 27
S
x
y
= + +
= +
=
.
Korzystając ze wzoru na sumę trzech początkowych wyrazów ciągu arytmetycznego,
otrzymujemy
1
19
3 27
2
a
+
⋅ =
.
Stąd
1
1
a
= − , zatem
1
x
= −
, 9
y
= .
Schemat oceniania III sposobu rozwiązania
Zdający otrzymuje............................................................................................................. 1 pkt
gdy wprowadzi oznaczenia
1
x
a
= ,
2
y
a
=
,
3
19 a
= i zapisze równanie
1
3
3 27
2
a
a
+
⋅ =
i na tym
poprzestanie lub dalej popełnia błędy.
Zdający otrzymuje............................................................................................................. 2 pkt
gdy obliczy:
1
−
=
x
i
9
=
y
.
Uwaga
Jeżeli zdający zapisze
1
−
=
x
i
9
=
y
bez obliczeń i nie uzasadni, że jest to jedyne
rozwiązanie, to otrzymuje 1 punkt.
Zadanie 28. (0–2)
I sposób rozwiązania
Sprowadzamy wyrażenie
sin
cos
2
cos
sin
α
α
α
α
+
= do wspólnego mianownika i otrzymujemy
2
2
sin
cos
2
sin cos
α
α
α
α
+
= . Korzystając z tożsamości
2
2
sin
cos
1
α
α
+
= , otrzymujemy
1
2
sin cos
α
α
= , a stąd
1
sin cos
.
2
α
α
=
Schemat oceniania I sposobu rozwiązania
Zdający otrzymuje ............................................................................................................ 1 pkt
gdy:
• sprowadzi wyrażenie
sin
cos
2
cos
sin
α
α
α
α
+
= do wspólnego mianownika i na tym
poprzestanie lub dalej popełnia błędy.
albo
• doprowadzi wyrażenie
sin
cos
2
cos
sin
α
α
α
α
+
= do postaci
2
2
sin
cos
2sin cos
α
α
α
α
+
=
i na tym poprzestanie lub dalej popełnia błędy.
Zdający otrzymuje ............................................................................................................ 2 pkt
gdy obliczy, że
1
sin cos
.
2
α
α
=
Użycie i tworzenie strategii
Zastosowanie prostych związków między funkcjami
trygonometrycznymi kąta ostrego
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
14
II sposób rozwiązania
Rysujemy trójkąt prostokątny, w którym oznaczamy długości przyprostokątnych
a
i
b
oraz
zaznaczamy kąt ostry
α
taki, że sin
α
=
a
c
lub cos
.
α
=
b
c
a
b
c
Korzystając z twierdzenia Pitagorasa, wyznaczamy długość przeciwprostokątnej:
2
2
2
c
a
b
=
+ .
Ponieważ
sin
cos
2
cos
sin
α
α
α
α
+
= , więc
2
a
b
b
a
+ = , czyli
2
2
2
a
b
a b
+
=
⋅
. Stąd
2
2
c
a b
=
⋅
.
Ponieważ
2
sin cos
α
α
⋅
=
a b
c
, to
1
sin cos
2
α
α
= .
III sposób rozwiązania
Rysujemy trójkąt prostokątny, w którym oznaczamy długości przyprostokątnych
a
i
b
oraz
zaznaczamy kąt ostry
α
taki, że sin
α
=
a
c
lub cos
.
α
=
b
c
a
b
c
Ponieważ
sin
cos
2
cos
sin
α
α
α
α
+
= , więc otrzymujemy kolejno:
2
a
b
b
a
+ = ,
2
2
2
a
b
ab
+
= ,
2
2
2
a
b
ab
+
=
,
stąd
(
)
2
0
a b
−
= , więc
a
b
=
. Zatem α 45
4
π
= ° = .
Wtedy
2
sin
sin 45
2
α
=
° =
i
2
cos
cos 45
2
α
=
° =
.
Obliczamy
2
2
1
sin cos
2
2
2
α
α
=
⋅
= .
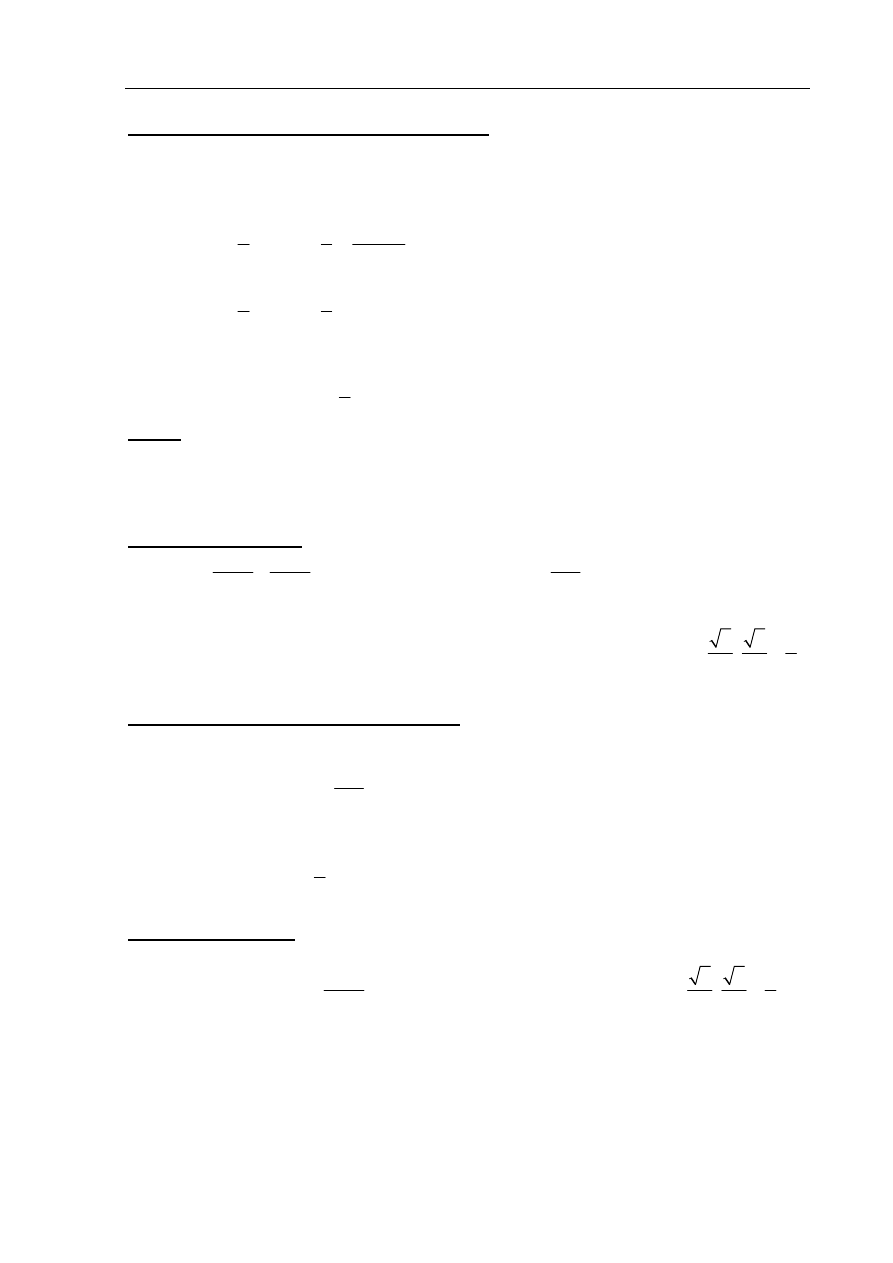
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
15
Schemat oceniania II i III sposobu rozwiązania
Zdający otrzymuje ............................................................................................................ 1 pkt
gdy narysuje trójkąt prostokątny o przyprostokątnych długości a i b, zaznaczy w tym trójkącie
kąt
α i zapisze:
• sin
α
=
a
c
, cos
α
=
b
c
i
2
2
2
a
b
a b
+
=
⋅
i na tym zakończy lub dalej popełnia błędy
albo
• sin
α
=
a
c
, cos
α
=
b
c
i
2
2
2
a
b
a b
+
=
⋅ i na tym zakończy lub dalej popełnia błędy.
Zdający otrzymuje ............................................................................................................ 2 pkt
gdy obliczy, że
1
sin cos
2
α
α
= .
Uwaga
Zdający może także odczytać z tablic przybliżone wartości funkcji trygonometrycznych
i obliczyć: sin 45 cos 45
0,7071 0,7071 0,4999 0,5
°⋅
° ≈
⋅
≈
≈
.
Nie akceptujemy innych przybliżeń.
IV sposób rozwiązania
Wyrażenie
sin
cos
2
cos
sin
α
α
α
α
+
= zapisujemy w postaci
1
tg
2
tg
α
α
+
= .
Stąd
2
tg
2tg
1 0
α
α
−
+ = .
Zatem tg
1
α
= i stąd
45
α
=
°
. Obliczamy wartość wyrażenia,
2
2
1
sin 45 cos 45
2
2
2
°⋅
° =
⋅
= .
Schemat oceniania IV sposobu rozwiązania
Zdający otrzymuje ............................................................................................................ 1 pkt
gdy zapisze równanie
1
tg
2
tg
α
α
+
= i na tym zakończy lub dalej popełnia błędy.
Zdający otrzymuje ............................................................................................................ 2 pkt
gdy obliczy
1
sin cos
2
α
α
= .
V sposób rozwiązania
Zauważamy, że suma liczby i jej odwrotności jest równa 2 wtedy i tylko wtedy, gdy ta liczba
jest równa 1. Zatem
sin
tg
1
cos
α
α
α
=
= i stąd
45
α
=
°
, a więc
2
2
1
sin 45 cos 45
2
2
2
°⋅
° =
⋅
= .
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
16
Schemat oceniania V sposobu rozwiązania
Zdający otrzymuje ............................................................................................................1 pkt
gdy zapisze, że suma liczby i jej odwrotności jest równa 2 wtedy i tylko wtedy, gdy ta liczba
jest równa 1, zapisze tg
1
α
= lub
sin
1
cos
α
α
= i na tym zakończy lub dalej popełnia błędy.
Zdający otrzymuje ............................................................................................................2 pkt
gdy obliczy
1
sin cos
2
α
α
= .
Uwaga
Jeżeli zdający w V sposobie rozwiązania zapisze bez uzasadnienia:
• tg
1
α
= lub
sin
1
cos
α
α
= lub
45
α
=
°
i na tym zakończy lub dalej popełnia błędy,
to otrzymuje 0 punktów.
• tg
1
α
= lub
sin
1
cos
α
α
= lub
45
α
=
°
i poprawnie obliczy
1
sin cos
2
α
α
= , to otrzymuje
1 punkt
.
Zadania 29. (0–2)
I sposób rozwiązania
Niech
CED
α
=
)
. Ponieważ trójkąt DCE jest równoramienny i
EC
CD
=
,
to
EDC
CED
α
=
=
)
)
. Zatem
180
2
α
=
° −
)DCE
.
Podobnie, ponieważ trójkąt ABE jest równoramienny i
AEB
EAB
β
=
=
)
)
,
to
180
2
β
=
° −
)ABE
.
Kąty ABE i DCE są kątami wewnętrznymi trapezu ABCD i
180
DCE
ABE
+
=
°
)
)
.
Stąd 180
2
180
2
180
α
β
° −
+
° −
=
°, czyli
2
2
180
α
β
+
=
°
90
α β
+ = ° .
Zatem
(
)
180
180
180
90
α β
α β
=
° −
−
=
° − − =
° −
+
= °
)
)
)
AED
CED
AEB
.
Schemat oceniania I sposobu rozwiązania
Zdający otrzymuje ............................................................................................................1 pkt
gdy napisze zależności między miarami kątów w trójkątach równoramiennych ABE i DCE,
np.
180
2
α
=
° −
)DCE
i
180
2
β
=
° −
)ABE
i na tym zakończy lub dalej popełnia błędy.
Zdający otrzymuje ............................................................................................................2 pkt
gdy poprawnie uzasadni, że
90
= °
)AED
.
Rozumowanie i argumentacja Uzasadnienie, że wskazany kąt jest prosty
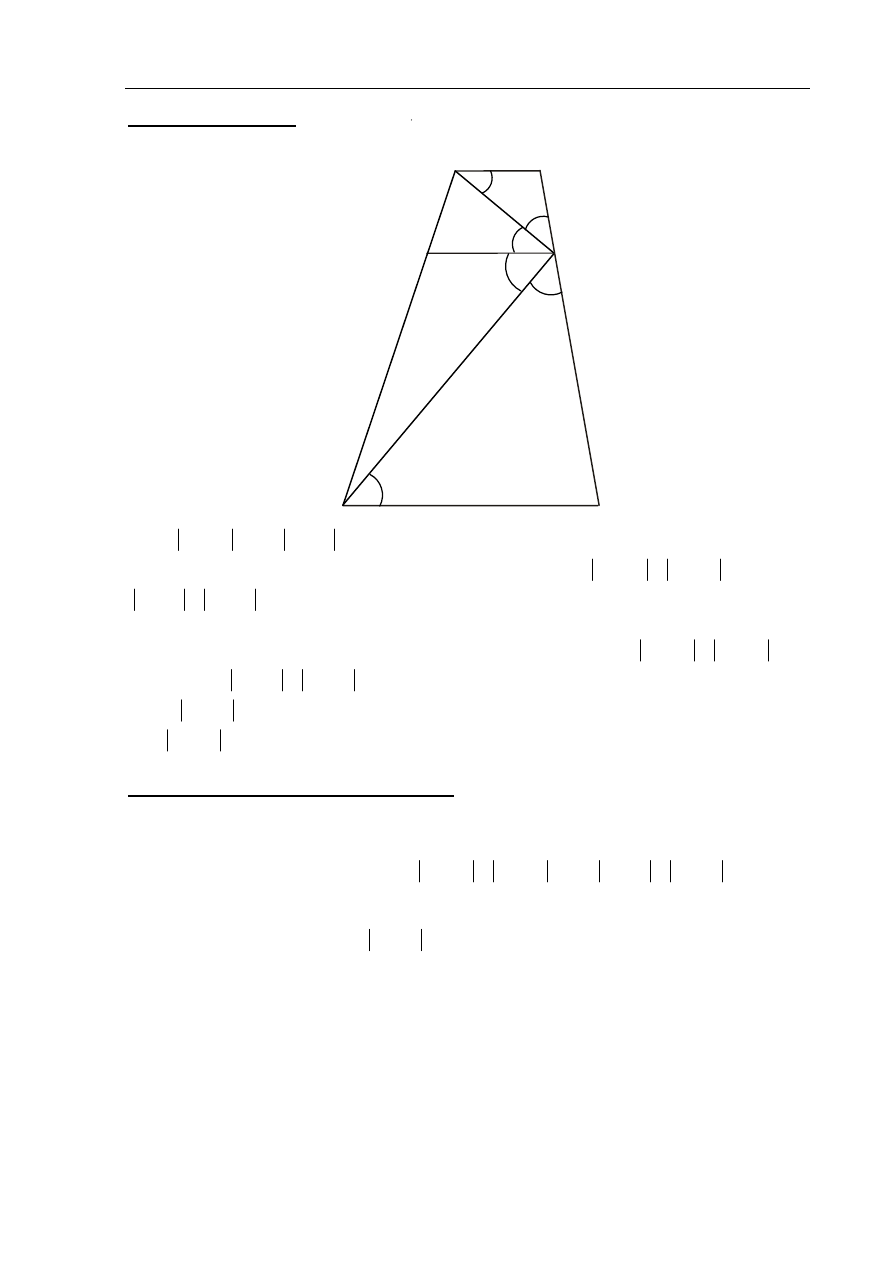
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
17
II sposób rozwiązania
Niech
CED
α
=
)
i
AEB
β
=
)
Trójkąty DCE i ABE są równoramienne. Zatem
EDC
CED
α
=
=
)
)
oraz
AEB
EAB
β
=
=
)
)
.
Dorysowujemy w danym trapezie odcinek EF równoległy do podstaw trapezu ABCD.
Kąty naprzemianległe CDE i DEF mają równe miary, zatem
EDC
DEF
α
=
=
)
)
.
Analogicznie
EAB
AEF
β
=
=
)
)
.
Zatem
180
2
2
α
β
=
° =
+
)BEC
, więc 90
α β
+ = ° .
Stąd
90
= °
)AED
, co kończy dowód.
Schemat oceniania II sposobu rozwiązania
Zdający otrzymuje ............................................................................................................ 1 pkt
gdy napisze, że trójkąty DCE i ABE są równoramienne, dorysuje odcinek EF równoległy
do podstaw trapezu ABCD i zapisze, że
EDC
DEF
α
=
=
)
)
i
EAB
AEF
β
=
=
)
)
.
Zdający otrzymuje ............................................................................................................ 2 pkt
gdy poprawnie uzasadni, że
90
= °
)AED
(uzasadnienie równości kątów może być
przedstawione na rysunku).
B
E
C
D
F
β
A
α
α
β
α
β
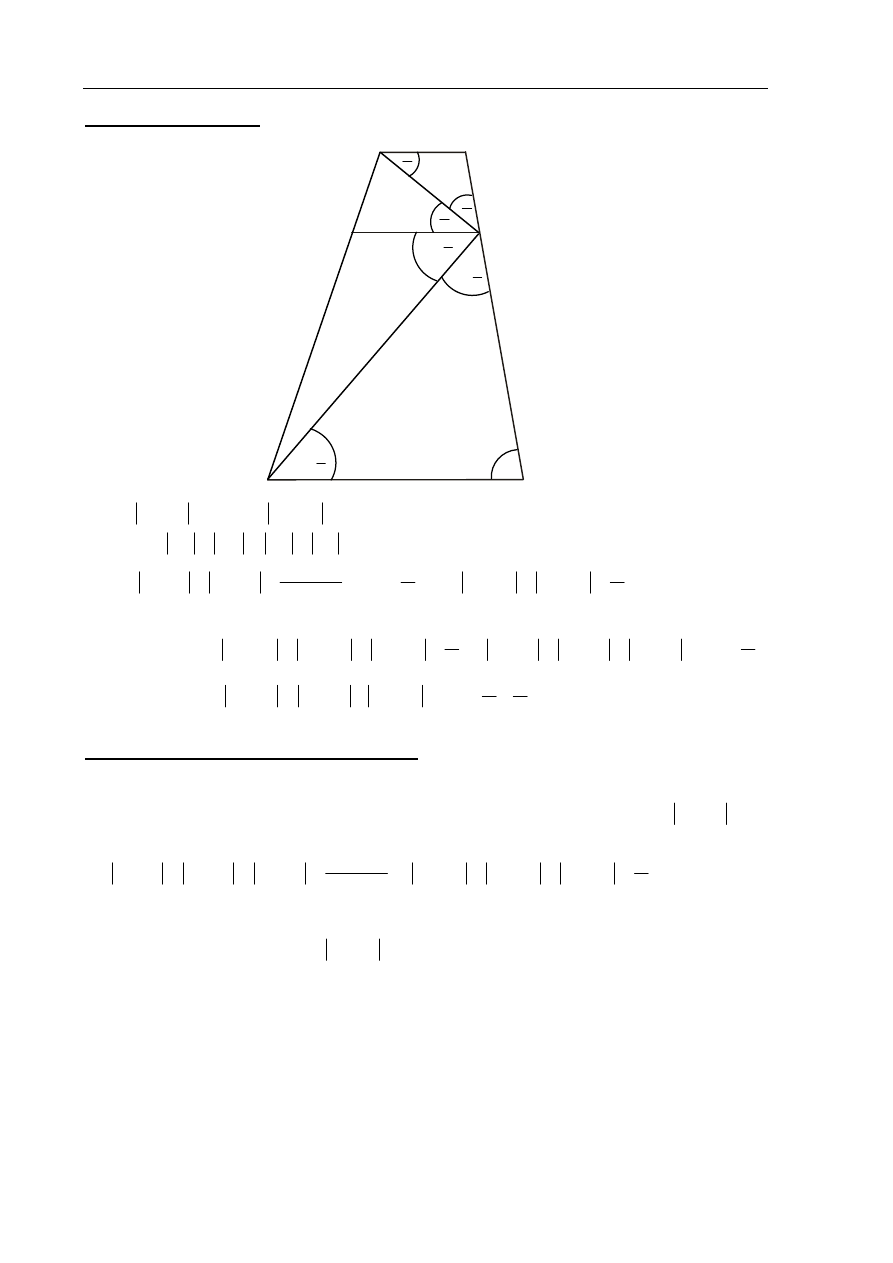
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
18
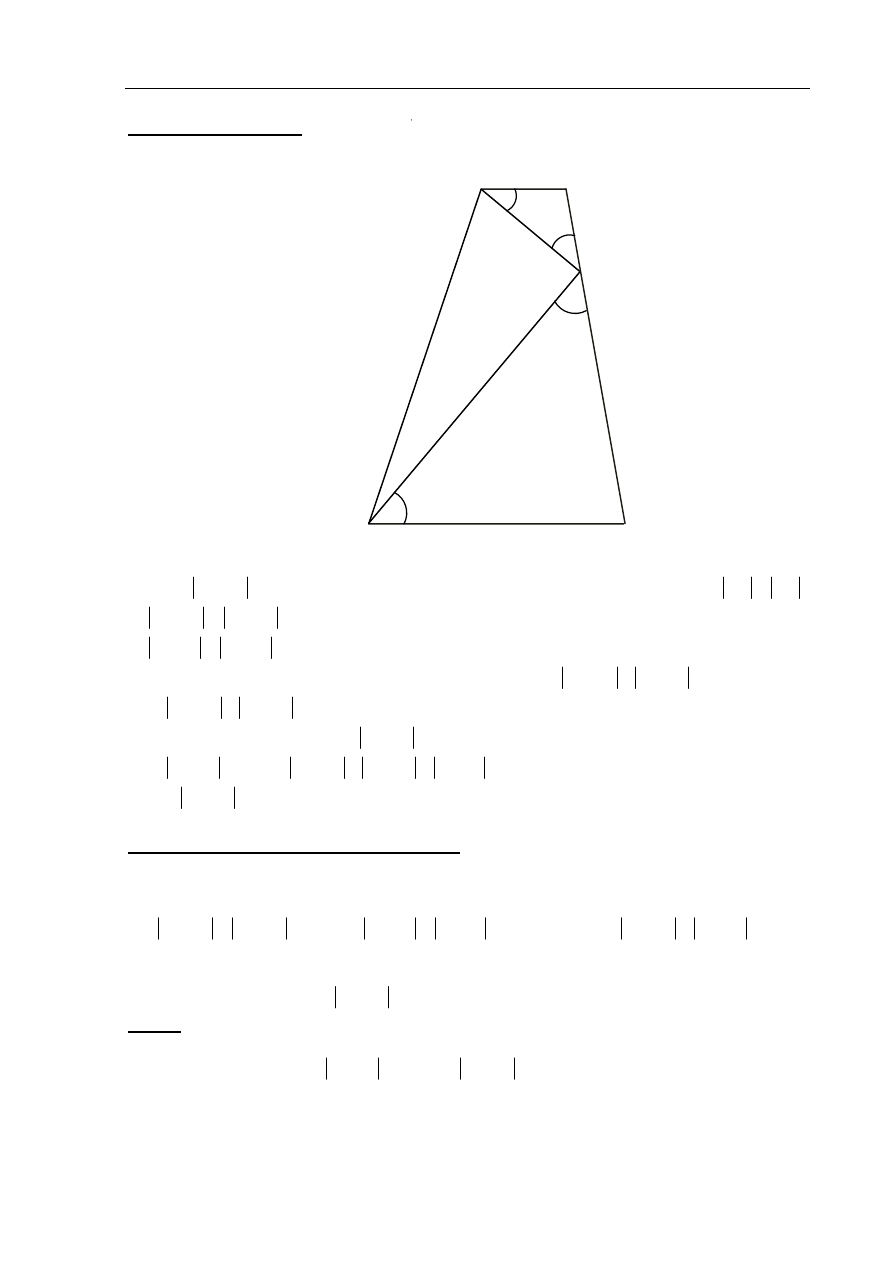
III sposób rozwiązania
Niech
ABC
α
=
)
, stąd
180
α
=
° −
)BCD
.
Ponieważ
CE
CD
=
i
EB
BA
=
, więc trójkąty DCE i ABE są równoramienne.
Zatem
180
90
2
2
α
α
° −
=
=
= ° −
)
)
AEB
EAB
oraz
2
EDC
CED
α
=
=
)
)
.
Dorysowujemy w danym trapezie odcinek EF równoległy do podstaw trapezu ABCD, więc
zachodzi równość:
2
EDC
CED
DEF
α
=
=
=
)
)
)
i
90
2
α
=
=
= ° −
)
)
)
AEB
EAB
AEF
Stąd otrzymujemy
90
90
2
2
AED
AEF
DEF
α α
=
+
= ° − +
= °
)
)
)
.
Schemat oceniania III sposobu rozwiązania
Zdający otrzymuje ............................................................................................................1 pkt
gdy napisze, że trójkąty DCE i ABE są równoramienne i przyjmie, że
ABC
α
=
)
,
dorysuje odcinek
EF równoległy do podstaw trapezu ABCD i zapisze,
że
180
2
α
° −
=
=
=
)
)
)
AEB
EAB
AEF
i
2
EDC
CED
DEF
α
=
=
=
)
)
)
.
Zdający otrzymuje ............................................................................................................2 pkt
gdy poprawnie uzasadni, że
90
= °
)AED
(uzasadnienie równości kątów może być
przedstawione na rysunku).
B
E
C
D
F
A
α
180
α
°−
2
α
2
α
90
2
α
°−
90
2
α
°−
2
α
90
2
α
°−
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
19
IV sposób rozwiązania
Niech
CED
α
=
)
. Ponieważ trójkąt DCE jest równoramienny i
EC
CD
=
,
to
EDC
CED
α
=
=
)
)
. Podobnie, ponieważ trójkąt ABE jest równoramienny,
to
AEB
EAB
β
=
=
)
)
Kąty ADC i BAD są kątami wewnętrznymi trapezu ABCD i
180
ADC
BAD
+
=
°
)
)
.
Stąd
(
)
180
ADE
EAD
α β
+
=
° −
+
)
)
.
Zatem w trójkącie DAE mamy:
(
)
180
180
AED
α β
α β
=
° −
° −
+
= +
⎡
⎤
⎣
⎦
)
.
Stąd
180
2
2
BEC
DEC
AED
AEB
α
β
=
° =
+
+
=
+
)
)
)
)
, czyli
90
α β
+ = ° .
Zatem
90
= °
)AED
.
Schemat oceniania IV sposobu rozwiązania
Zdający otrzymuje ............................................................................................................ 1 pkt
gdy zapisze zależności między miarami kątów w trójkątach równoramiennych ABE i DCE,
np.
EDC
CED
α
=
=
)
)
oraz
AEB
EAB
β
=
=
)
)
i zapisze, że
180
ADC
BAD
+
=
°
)
)
.
Zdający otrzymuje ............................................................................................................ 2 pkt
gdy poprawnie uzasadni, że
90
= °
)AED
.
Uwaga
Jeżeli zdający przyjmie dodatkowe założenia o trapezie ABCD, przez co rozważa tylko
szczególny przypadek, np.
90
= °
)ABC
lub
45
=
°
)DEC
, to za całe rozwiązanie otrzymuje
0 punktów
.
B
E
C
D
β
A
α
α
β
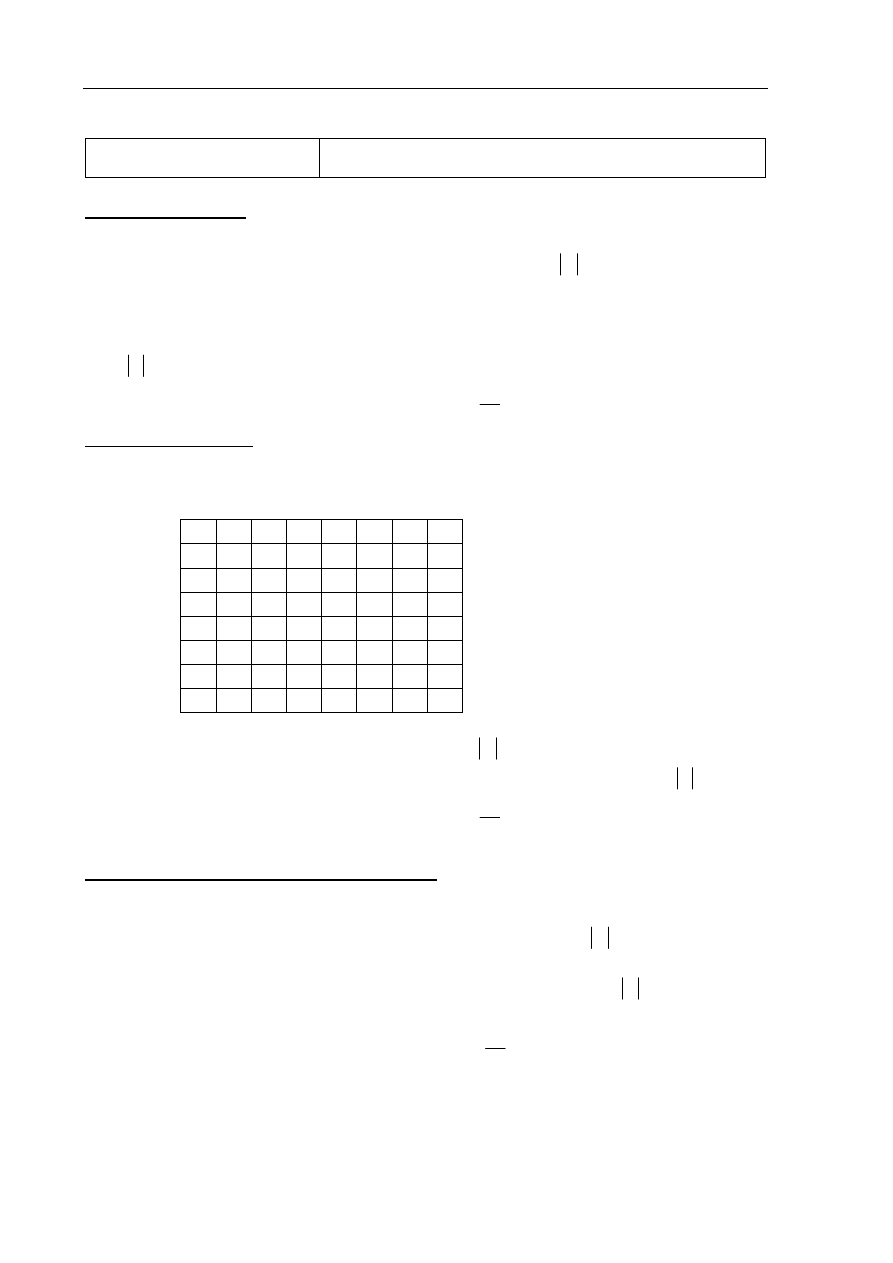
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
20
Zadanie 30. (0–2)
I sposób rozwiązania
(metoda klasyczna)
Zdarzeniami elementarnymi są wszystkie pary
(
)
,
a b
liczb z podanego zbioru. Jest to model
klasyczny. Obliczamy liczbę wszystkich zdarzeń elementarnych:
2
7
Ω =
.
Obliczamy liczbę zdarzeń elementarnych sprzyjających zdarzeniu A polegającym na
otrzymaniu liczb, których suma jest podzielna przez 3, np. wypisując je i zliczając:
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) ( ) ( ) ( ) ( ) ( ) ( )
{
}
1,2 , 1,5 , 2,1 , 2,4 , 2,7 , 3,3 , 3,6 , 4,2 , 4,5 5,1 , 5,4 , 5,7 , 6,3 , 6,6 , 7,2 , 7,5 ,
A
=
czyli
16
A
=
Obliczamy prawdopodobieństwo zdarzenia A:
16
( )
49
P A
=
.
II sposób rozwiązania
(metoda tabeli)
Zdarzeniami elementarnymi są wszystkie pary
(
)
,
a b
liczb z podanego zbioru. Jest to model
klasyczny. Tworzymy tabelę ilustrującą sytuację opisaną w zadaniu
1 2 3 4 5 6 7
1
X X
2 X X X
3
X X
4
X X
5 X X X
6
X X
7
X X
Obliczamy liczbę wszystkich zdarzeń elementarnych:
2
7
Ω =
.
Zliczamy oznaczone krzyżykami zdarzenia elementarne sprzyjające zdarzeniu A:
16
A
=
.
Obliczamy prawdopodobieństwo zdarzenia A:
16
( )
49
P A
=
.
Schemat oceniania I i II sposobu rozwiązania
Zdający otrzymuje ............................................................................................................1 pkt
gdy
• obliczy liczbę wszystkich możliwych zdarzeń elementarnych:
2
7
49
Ω =
=
albo
• obliczy liczbę zdarzeń elementarnych sprzyjających zdarzeniu A :
16
A
=
Zdający otrzymuje ............................................................................................................2 pkt
gdy obliczy prawdopodobieństwo zdarzenia A:
16
( )
49
P A
=
.
Użycie i tworzenie strategii
Obliczenie prawdopodobieństwa zdarzenia
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
21
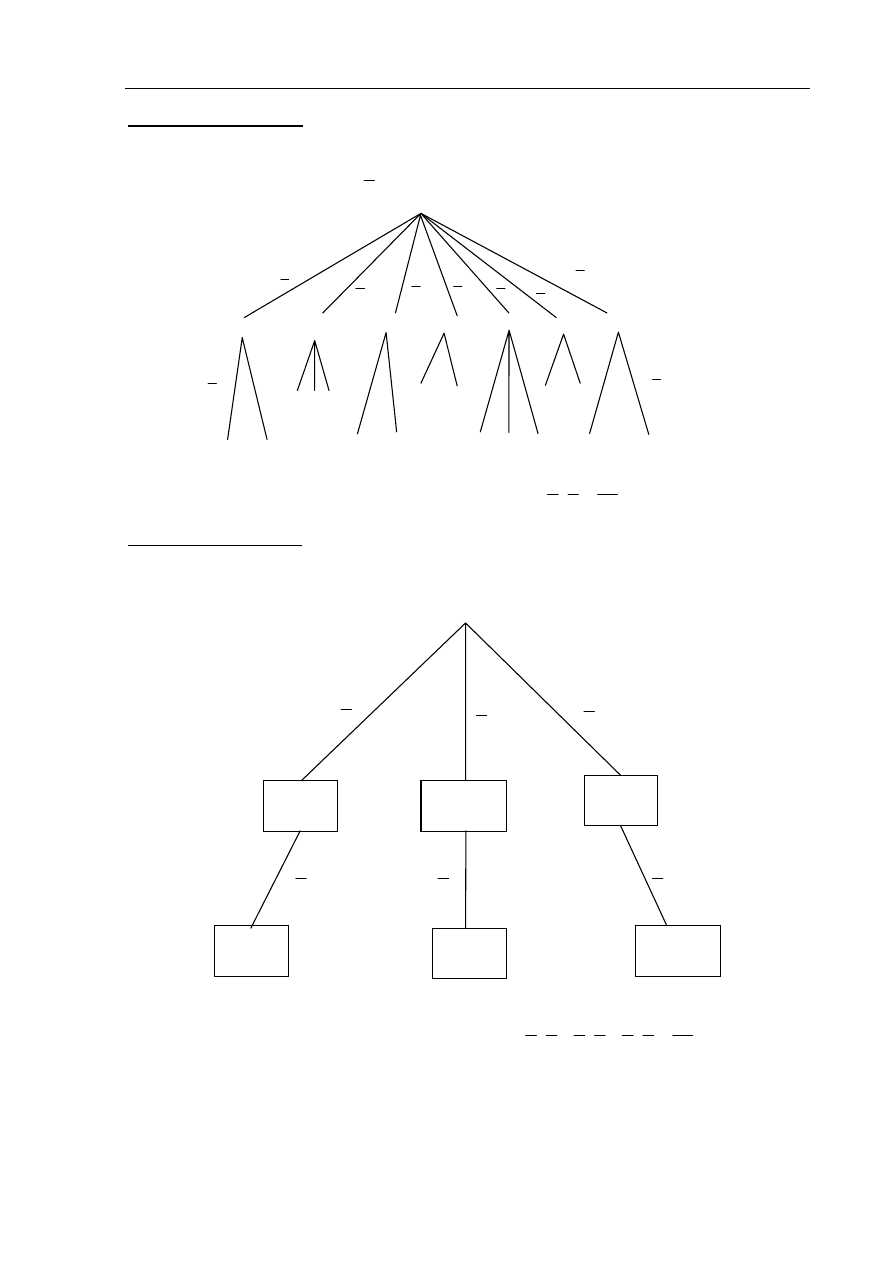
III sposób rozwiązania
(metoda drzewa)
Rysujemy drzewo, uwzględniając tylko istotne gałęzie. Prawdopodobieństwo na każdym
odcinku tego drzewa jest równe
1
7
.
Obliczamy prawdopodobieństwo zdarzenia A:
1 1
16
( ) 16
7 7
49
P A
=
⋅ ⋅ =
.
IV sposób rozwiązania
(metoda drzewa)
Rysujemy drzewo, uwzględniając tylko istotne gałęzie i zapisujemy na nich
prawdopodobieństwo.
Obliczamy prawdopodobieństwo zdarzenia A:
( )
2 2 3 2 2 3 16
7 7 7 7 7 7
47
P A
= ⋅ + ⋅ + ⋅ =
1
7
1
2 5
2
3
4
5
6
7
1
7
1
7
1
7
1
7
1
7
1
7
1
7
3 6
1 4 7
2 5
1 4 7
2 5
3 6
1
7
{ }
3, 6
{
}
1, 4,7
{ }
2,5
{ }
3, 6
{ }
2,5
{
}
1, 4,7
2
7
3
7
2
7
2
7
2
7
3
7
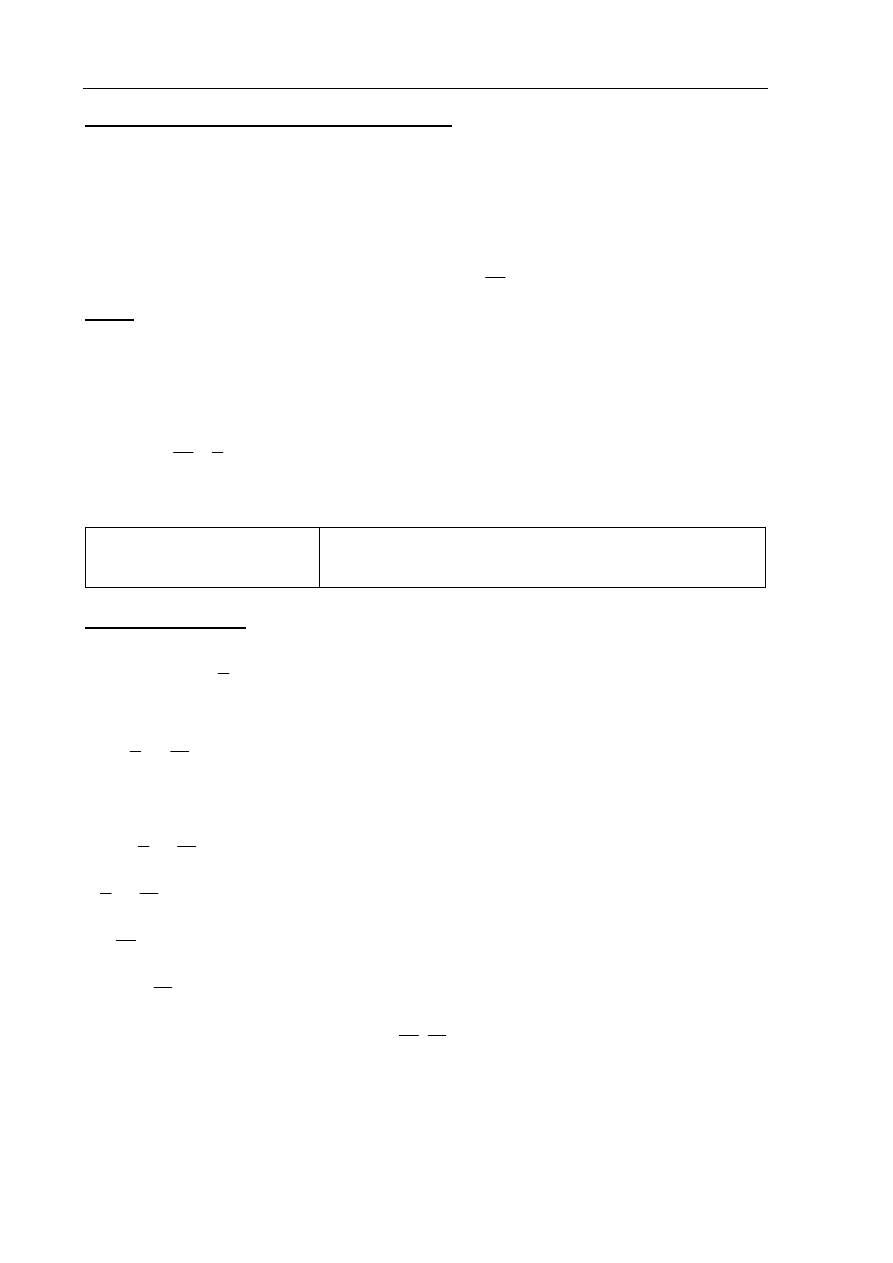
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
22
Schemat oceniania III i IV sposobu rozwiązania
Zdający otrzymuje ............................................................................................................1 pkt
gdy:
• narysuje pełne drzewo i przynajmniej na jednej gałęzi opisze prawdopodobieństwo
albo
• narysuje drzewo tylko z istotnymi gałęziami.
Zdający otrzymuje ............................................................................................................2 pkt
gdy obliczy prawdopodobieństwo zdarzenia A:
16
( )
49
P A
=
.
Uwagi
1. Jeśli zdający rozwiąże zadanie do końca i otrzyma ( ) 1
P A
> , to otrzymuje za całe
rozwiązanie 0 punktów.
2. Jeżeli zdający opuści przez nieuwagę w rozwiązaniu niektóre gałęzie i konsekwentnie
obliczy prawdopodobieństwo, to za całe rozwiązanie otrzymuje 1 punkt.
3. Jeżeli zdający poprawnie obliczy prawdopodobieństwo i błędnie skróci ułamek, np.
16
4
( )
49
7
P A
=
= , to otrzymuje 2 punkty.
Zadanie 31. (0–4)
I sposób rozwiązania
Wyznaczamy współczynnik kierunkowy m prostej prostopadłej do prostej o równaniu
2
3
y
x
=
− :
1
2
m
= − .
Zapisujemy równanie prostej prostopadłej do stycznej i przechodzącej przez punkt
( )
3,7
S
=
:
2
17
2
1 +
−
=
x
y
.
Zapisujemy i rozwiązujemy układ równań:
2
3
1
17
2
2
y
x
y
x
=
−
⎧
⎪
⎨
= −
+
⎪⎩
1
17
2
3
2
2
x
x
−
+
=
−
5
23
=
x
Stąd
5
31
=
y
.
Zatem punkt styczności ma współrzędne:
23 31
,
5 5
⎛
⎞
⎜
⎟
⎝
⎠
.
Użycie i tworzenie strategii
Wyznaczenie współrzędnych punktu styczności prostej
z okręgiem
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
23
Schemat oceniania I sposobu rozwiązania
Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego
rozwiązania zadania .......................................................................................................... 1 pkt
Zapisanie współczynnika kierunkowego prostej prostopadłej do prostej o równaniu
2
3
y
x
=
− , np.
1
2
m
= − .
Rozwiązanie, w którym jest istotny postęp ..................................................................... 2 pkt
Zapisanie układ równań
2
3
1
17
2
2
=
−
⎧
⎪
⎨
= −
+
⎪⎩
y
x
y
x
Pokonanie zasadniczych trudności zadania .................................................................... 3 pkt
Przekształcenie układu równań do równania z jedną niewiadomą, np.
1
17
2
3
2
2
x
x
−
+
=
− lub
1
3 17
4
4
2
y
y
= −
− +
.
Rozwiązanie pełne ............................................................................................................. 4 pkt
Obliczenie współrzędnych punktu styczności:
23 31
,
5 5
⎛
⎞
⎜
⎟
⎝
⎠
.
Uwaga
Jeśli zdający zapisał układ równań liniowych i odgadł jego rozwiązanie, to otrzymuje
4 punkty
II sposób rozwiązania
Obliczamy odległość d środka okręgu
)
7
,
3
(
=
S
od prostej
2
3
y
x
=
− :
6 7 3
4
4 1
5
d
− −
=
=
+
.
Punkt
( , 2
3)
P
x
x
=
− jest punktem styczności okręgu o środku w punkcie
)
7
,
3
(
=
S
i prostej
2
3
y
x
=
− . Zatem PS
d
= oraz
2
2
(
3)
(2
10)
PS
x
x
=
−
+
−
.
Przekształcamy równanie
5
4
)
10
2
(
)
3
(
2
2
=
−
+
−
x
x
do postaci
0
5
16
109
46
5
2
=
−
+
−
x
x
Rozwiązujemy równanie
0
5
4
105
46
5
2
=
+
−
x
x
, stąd
5
23
=
x
.
Zatem punkt styczności ma współrzędne:
23 31
,
5 5
P
⎛
⎞
= ⎜
⎟
⎝
⎠
.
Schemat oceniania II sposobu rozwiązania
Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego
rozwiązania zadania .......................................................................................................... 1 pkt
• obliczenie odległości punktu
S
od danej prostej
6 7 3
4
4 1
5
d
− −
=
=
+
albo
• zapisanie długości odcinka
PS
:
2
2
(
3)
(2
10)
PS
x
x
=
−
+
−
.
Rozwiązanie, w którym jest istotny postęp ..................................................................... 2 pkt
Zapisanie układ równań, np.
(
)
2
2
2
3
4
(
3)
7
5
y
x
x
y
=
−
⎧
⎪
⎨
−
+
−
=
⎪⎩
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
24
Pokonanie zasadniczych trudności zadania.....................................................................3 pkt
Zapisanie równania z jedną niewiadomą, np.
0
5
4
105
46
5
2
=
+
−
x
x
albo
5
4
)
10
2
(
)
3
(
2
2
=
−
+
−
x
x
.
Rozwiązanie pełne..............................................................................................................4 pkt
Obliczenie współrzędnych punktu P styczności:
23 31
,
5 5
⎛
⎞
⎜
⎟
⎝
⎠
.
III sposób rozwiązania
Punkt
( )
,
P
x y
=
jest punktem styczności okręgu o środku
)
7
,
3
(
=
S
i prostej
2
3
y
x
=
− .
Zapisujemy układ równań:
2
2
2
(
3)
(
7)
2
3
x
y
r
y
x
⎧ −
+
−
=
⎨
=
−
⎩
Przekształcamy układ równań do równania kwadratowego z niewiadomą x:
2
2
2
(
3)
(2
10)
x
x
r
−
+
−
=
2
2
5
46
109
0
x
x
r
−
+
−
= .
Zapisujemy warunek
0
Δ = , dla którego okrąg ma jeden punkt wspólny z prostą
2
3
y
x
=
−
i obliczamy
2
r :
2
64 20r
Δ = − +
,
2
20
64 0
r
−
= ,
2
20
64
r
=
,
2
64 16
20
5
r
=
=
.
Rozwiązujemy równanie:
0
5
16
109
46
5
2
=
−
+
−
x
x
0
5
4
105
46
5
2
=
+
−
x
x
5
23
=
x
.
Zatem punkt styczności ma współrzędne:
23 31
,
5 5
P
⎛
⎞
= ⎜
⎟
⎝
⎠
.
Schemat oceniania III sposobu rozwiązania
Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego
rozwiązania zadania...........................................................................................................1 pkt
Zapisanie układu równań i warunku pozwalającego wyznaczyć promień okręgu:
2
2
2
(
3)
(
7)
2
3
x
y
r
y
x
⎧ −
+
−
=
⎨
=
−
⎩
Rozwiązanie, w którym jest istotny postęp......................................................................2 pkt
Przekształcenie układu do równania z jedną niewiadomą
2
2
5
46
109
0
x
x
r
−
+
−
= , zapisanie
warunku 0
Δ = i obliczenie
2
r :
2
16
5
r
=
.
Pokonanie zasadniczych trudności zadania.....................................................................3 pkt
Zapisanie równania kwadratowego, np.
0
5
4
105
46
5
2
=
+
−
x
x
.
Rozwiązanie pełne..............................................................................................................4 pkt
Obliczenie współrzędnych punktu styczności:
23 31
,
5 5
P
⎛
⎞
= ⎜
⎟
⎝
⎠
.

Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
25
Uwaga
Jeśli zdający popełnił błąd rachunkowy, przekształcając układ równań do równania
kwadratowego, rozwiązał to równanie i otrzymał dwa punkty styczności, to za całe
rozwiązanie otrzymuje 2 punkty.
Zadanie 32. (0–5)
I sposób rozwiązania
Niech x oznacza liczbę dni wędrówki, y – liczbę kilometrów przebytych każdego dnia przez
turystę. Drogę przebytą przez turystę opisujemy równaniem
112
x y
⋅ =
.
Turysta może przeznaczyć na wędrówkę o 3 dni więcej, idąc każdego dnia o 12 km mniej,
wówczas zapisujemy równanie:
(
) (
)
3
12
112
x
y
+ ⋅
−
=
.
Zapisujemy układ równań, np.
(
) (
)
112
3
12
112
x y
x
y
⋅ =
⎧⎪
⎨ + ⋅ − =
⎪⎩
Z pierwszego równania wyznaczamy
112
y
x
=
112
x
y
=
podstawiamy do drugiego równania i rozwiązujemy
(
)
112
3
12
112
x
x
⎛
⎞
+
−
=
⎜
⎟
⎝
⎠
Przekształcamy to równanie do równania
kwadratowego, np.
2
3
28 0
x
x
+
−
= .
2
9 112 121 11
Δ = +
=
=
1
3 11
7
2
x
− −
=
= − sprzeczne z zał.
0
x
>
2
3 11
4
2
x
− +
=
=
Obliczamy y:
112
28
4
y
=
=
Odp.: Turysta przechodził dziennie 28 km.
(
)
112
3
12
112
y
y
⎛
⎞
+
−
=
⎜
⎟
⎝
⎠
Przekształcamy to równanie do równania
kwadratowego, np.
2
12
448 0
y
y
−
−
=
2
144 1792 1936 44
Δ =
+
=
=
1
12 44
16
2
y
−
=
= − sprzeczne z zał.
0
y
>
2
12 44
28
2
y
+
=
=
Odp.: Turysta przechodził dziennie 28 km.
II sposób rozwiązania
Niech x oznacza liczbę dni wędrówki, y – liczbę kilometrów przebytych każdego dnia przez
turystę. Drogę przebytą przez turystę opisujemy równaniem
112
x y
⋅ =
.
Turysta może przeznaczyć na wędrówkę o 3 dni więcej, idąc każdego dnia o 12 km mniej,
wówczas zapisujemy równanie:
(
) (
)
3
12
112
x
y
+ ⋅
−
=
.
Zapisujemy układ równań, np.
(
) (
)
112
3
12
112
x y
x
y
⋅ =
⎧⎪
⎨ + ⋅ − =
⎪⎩
Stąd otrzymujemy kolejno
112
12
3
36 112
x y
x y
x
y
⋅ =
⎧
⎨ ⋅ − + − =
⎩
Modelowanie matematyczne
Rozwiązanie zadania umieszczonego w kontekście
praktycznym, prowadzącego do równania kwadratowego
z jedną niewiadomą
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
26
112
112 12
3
36 112
x y
x
y
⋅ =
⎧
⎨
−
+
−
=
⎩
112
12
3
36 0
x y
x
y
⋅ =
⎧
⎨− + − =
⎩
W równaniu 12
3
36 0
x
y
−
+
−
= obie strony dzielimy przez
( )
3
−
.
Otrzymujemy 4
12 0
x
y
− +
= , stąd wyznaczamy
4
12
y
x
=
+
1
3
4
x
y
=
−
podstawiamy do równania pierwszego i rozwiązujemy
(
)
4
12
112
x
x
⋅
+
=
2
4
12
112 0
x
x
+
−
=
2
3
28 0
x
x
+
−
=
2
9 112 121 11
Δ = +
=
=
1
3 11
7
2
x
− −
=
= − sprzeczne z zał.
0
x
>
2
3 11
4
2
x
− +
=
=
Obliczamy y:
4 4 12 28
y
= ⋅ +
=
Odp.: Turysta przechodził dziennie 28 km.
1
3
112
4
y
y
⎛
⎞
− ⋅ =
⎜
⎟
⎝
⎠
2
1
3
112 0
4
y
y
−
−
=
2
12
448 0
y
y
−
−
=
2
144 1792 1936 44
Δ =
+
=
=
1
12 44
16
2
y
−
=
= − sprzeczne z zał.
0
y
>
2
12 44
28
2
y
+
=
=
Odp.: Turysta przechodził dziennie 28 km.
Schemat oceniania I i II sposobu rozwiązania
Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego
rozwiązania zadania
......................................................................................................... 1 pkt
Zapisanie zależności między przebytą drogą, liczbą dni wędrówki oraz liczbą kilometrów
przebytych każdego dnia przez turystę, np.:
•
(
) (
)
3
12
112
x
y
+ ⋅
−
=
albo
•
112
x y
⋅ =
.
Rozwiązanie, w którym jest istotny postęp
.................................................................... 2 pkt
Zapisanie układu równań z niewiadomymi x i y – odpowiednio: liczbą dni wędrówki i liczbą
kilometrów przebytych każdego dnia przez turystę, np.
(
) (
)
112
3
12
112
x y
x
y
⋅ =
⎧⎪
⎨ + ⋅ − =
⎪⎩
Pokonanie zasadniczych trudności zadania
................................................................... 3 pkt
Zapisanie równania z jedną niewiadomą x lub y, np:
(
)
112
3
12
112
x
x
⎛
⎞
+
−
=
⎜
⎟
⎝
⎠
lub
(
)
112
3
12
112
y
y
⎛
⎞
+
−
=
⎜
⎟
⎝
⎠
, lub
(
)
4
12
112
x
x
⋅
+
=
,
lub
1
3
112
4
y
y
⎛
⎞
− ⋅ =
⎜
⎟
⎝
⎠
Uwaga
Zdający nie musi zapisywać układu równań, może bezpośrednio zapisać równanie z jedną
niewiadomą.

Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
27
Rozwiązanie zadania do końca lecz z usterkami, które jednak nie przekreślają
poprawności rozwiązania (np. błędy rachunkowe)
...................................................... 4 pkt
• rozwiązanie równania z niewiadomą x bezbłędnie i nie obliczenie liczby kilometrów
przebytych każdego dnia przez turystę
albo
• rozwiązanie równania z niewiadomą x lub y z błędem rachunkowym i konsekwentne
obliczenie liczby kilometrów przebytych każdego dnia przez turystę.
Rozwiązanie pełne
........................................................................................................... 5 pkt
Obliczenie liczby kilometrów przebytych każdego dnia przez turystę: 28 km.
III sposób rozwiązania
Niech x oznacza liczbę dni wędrówki, y – liczbę kilometrów przebytych każdego dnia przez
turystę. Liczbę kilometrów przebytych każdego dnia przez turystę opisujemy równaniem
112
y
x
=
.
Turysta może przeznaczyć na wędrówkę o 3 dni więcej, idąc każdego dnia o 12 km mniej,
wówczas zapisujemy równanie:
112
112
12
3
x
x
=
+
+
.
Przekształcamy to równanie do postaci
2
3
28 0
x
x
+
−
= .
Rozwiązaniem równania są:
1
3 11
7
2
x
− −
=
= − sprzeczne z założeniem
0
x
>
i
2
3 11
4
2
x
− +
=
=
Obliczamy y:
112
28
4
y
=
=
Schemat oceniania III sposobu rozwiązania
Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego
rozwiązania zadania
........................................................................................................ 1 pkt
Przyjęcie oznaczeń: x - liczba dni wędrówki, y – liczba kilometrów przebytych każdego dnia
przez turystę i zapisanie zależności, np.
•
112
y
x
=
albo
•
112
12
3
y
x
=
+
+
.
Pokonanie zasadniczych trudności zadania
.................................................................. 3 pkt
Zapisanie równania z jedną niewiadomą:
112
112
12
3
x
x
=
+
+
.
Rozwiązanie zadania do końca lecz z usterkami, które jednak nie przekreślają
poprawności rozwiązania (np. błędy rachunkowe)
...................................................... 4 pkt
• rozwiązanie równania z niewiadomą x bezbłędnie i nie obliczenie liczby kilometrów
przebytych każdego dnia przez turystę
albo
• rozwiązanie równania z niewiadomą x błędem rachunkowym i konsekwentne
obliczenie liczby kilometrów przebytych każdego dnia przez turystę, przy czym
obliczona liczba kilometrów musi być większa od 12.
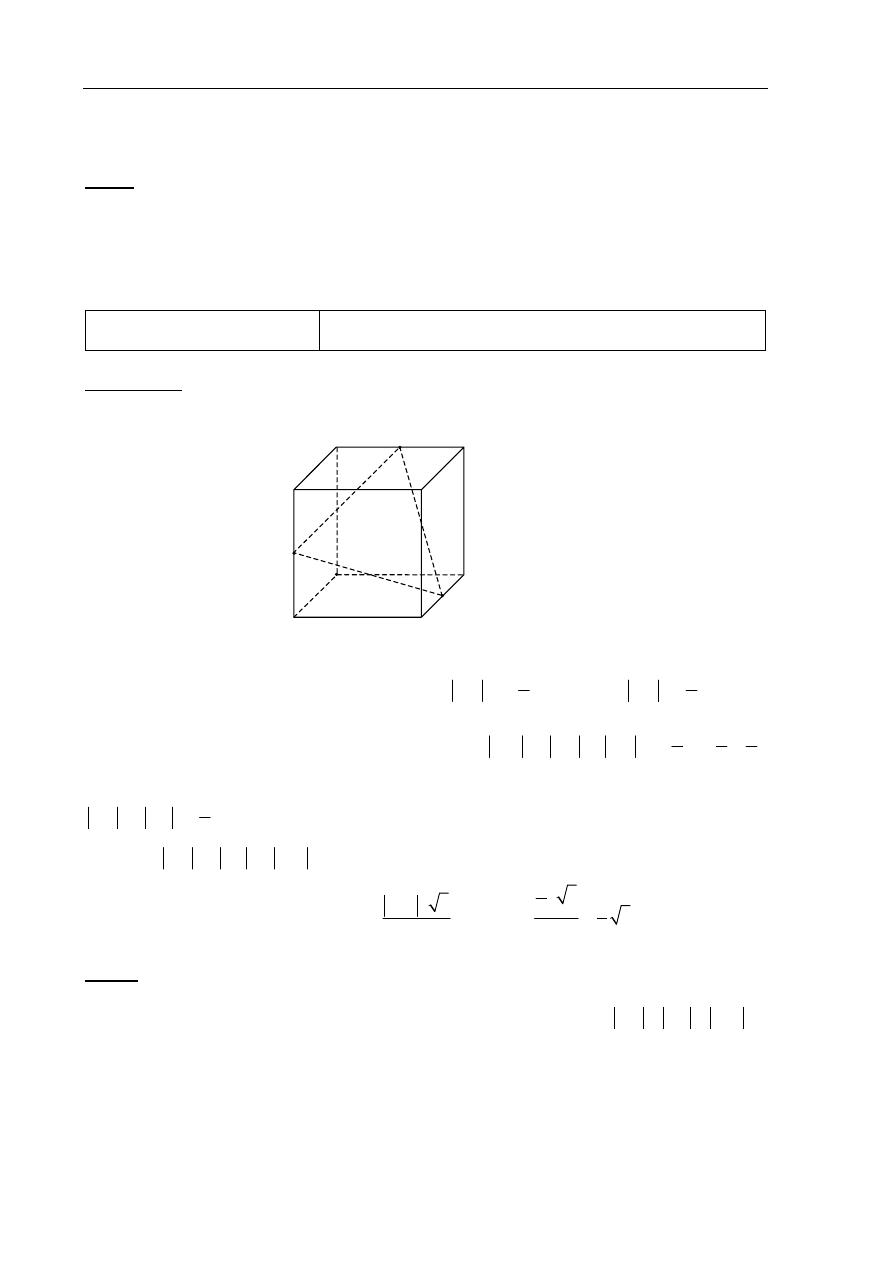
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
28
Rozwiązanie pełne
............................................................................................................ 5 pkt
Obliczenie liczby kilometrów przebytych każdego dnia przez turystę: 28 km.
Uwagi
1. Jeżeli zdający porównuje wielkości różnych typów, to otrzymuje 0 punktów.
2. Jeżeli zdający odgadnie liczbę kilometrów przebytych każdego dnia przez turystę i nie
uzasadni, że jest to jedyne rozwiązanie, to otrzymuje 1 punkt.
Zadanie 33. (0–4)
Rozwiązanie
Trójkąt ABK jest trójkątem prostokątnym, zatem
2
2
1
1
2
AK
⎛ ⎞
=
+
⎜ ⎟
⎝ ⎠
. Stąd
2
5
4
AK
= .
Trójkąt MAK jest trójkątem prostokątnym, zatem
2
2
2
2
1
5
3
2
4
2
MK
MA
AK
⎛ ⎞
=
+
=
+ =
⎜ ⎟
⎝ ⎠
.
Analogicznie dla trójkątów MEL i LGK obliczamy kwadraty długości boków ML i KL:
2
2
3
2
ML
KL
=
= .
Ponieważ
2
2
2
ML
KL
MK
=
=
, więc trójkąt KLM jest równoboczny.
Zatem jego pole wyraża się wzorem
2
3
4
MK
P
=
, stąd
3
3
3
2
3
4
8
P
⋅
=
=
.
Uwaga
Zdający nie musi obliczać kwadratów długości boków ML i KL. Wystarczy, że korzystając
z przystawania trójkątów MAK , MEL , LGK uzasadni równość boków:
ML
KL
MK
=
=
.
Użycie i tworzenie strategii Wyznaczenie
związków miarowych w sześcianie
L
H
G
F
E
M
K
D
A
B
C
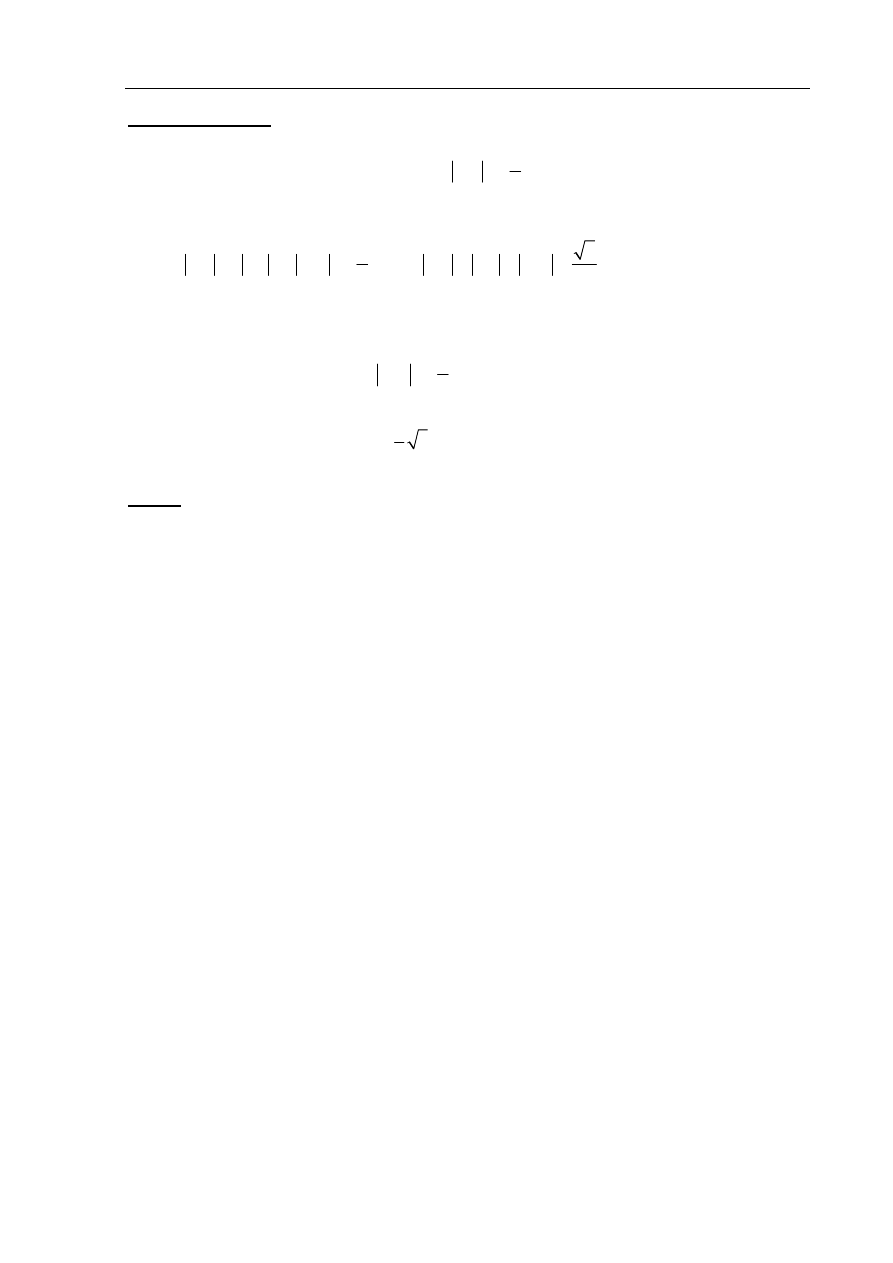
Egzamin maturalny z matematyki – poziom podstawowy
Kryteria oceniania odpowiedzi
29
Schemat oceniania
Rozwiązanie, w którym jest istotny postęp ..................................................................... 2 pkt
Obliczenie kwadratu długości odcinka AK :
2
5
4
AK
=
.
Pokonanie zasadniczych trudności zadania .................................................................... 3 pkt
• obliczenie kwadratów długości lub długości boków trójkąta KLM:
2
2
2
3
2
ML
KL
MK
=
=
=
lub
6
2
ML
KL
MK
=
=
=
i na tym poprzestanie lub
dalej popełni błędy
albo
• zauważenie, że trójkąt KLM jest równoboczny i obliczenie kwadratu długości jednego
z boków tego trójkąta, np.
2
3
2
MK
= .
Rozwiązanie pełne ............................................................................................................. 4 pkt
Obliczenie pola trójkąta KLM :
3
3
8
P
=
.
Uwaga
Akceptujemy rozwiązanie, w którym zdający przyjmuje, że długość krawędzi sześcianu jest
oznaczona literą l.
Document Outline
- Centralna Komisja Egzaminacyjna
- Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu.
- z kodem
- WPISUJE ZDAJĄCY
- Z MATEMATYKI
- POZIOM PODSTAWOWY
- 1. Sprawdź, czy arkusz egzaminacyjny zawiera 20 stron (zadania 1–33). Ewentualny brak zgłoś przewodniczącemu zespołu nadzorującego egzamin.
- 2. Rozwiązania zadań i odpowiedzi wpisuj w miejscu na to przeznaczonym.
- 3. Odpowiedzi do zadań zamkniętych (1–23) przenieś na kartę odpowiedzi, zaznaczając je w części karty przeznaczonej dla zdającego. Zamaluj pola do tego przeznaczone. Błędne zaznaczenie otocz kółkiem i zaznacz właściwe.
- 4. Pamiętaj, że pominięcie argumentacji lub istotnych obliczeń w rozwiązaniu zadania otwartego (24–33) może spowodować, że za to rozwiązanie nie będziesz mógł dostać pełnej liczby punktów.
- 5. Pisz czytelnie i używaj tylko długopisu lub pióra z czarnym tuszem lub atramentem.
- 6. Nie używaj korektora, a błędne zapisy wyraźnie przekreśl.
- 7. Pamiętaj, że zapisy w brudnopisie nie będą oceniane.
- 8. Możesz korzystać z zestawu wzorów matematycznych, cyrkla i linijki oraz kalkulatora.
- 9. Na karcie odpowiedzi wpisz swój numer PESEL i przyklej naklejkę z kodem.
- 10. Nie wpisuj żadnych znaków w części przeznaczonej dla egzaminatora.
Wyszukiwarka
Podobne podstrony:
matematyka egazmin próbny podstawowy 1
matematyka egazmin CKE rozszerzony
bryły obrotowe powtorzenie - lekcja otwarta w III g, Matematyka dla Szkoły Podstawowej, Gimnazjum
Arkusz maturalny z matematyki na poziomie podstawowym rozwiazania
Pole powierzchni i objetość brył - scenariusz III g, Matematyka dla Szkoły Podstawowej, Gimnazjum
Geometria analityczna, Matematyka dla Szkoły Podstawowej
projekt - ZBIERANIE I OPRACOWYWANIE DANYCH, Matematyka dla Szkoły Podstawowej, Gimnazjum
ELEMENTY STATYSTYKI OPISOWEJ - SCENARIUSZ, Matematyka dla Szkoły Podstawowej, Gimnazjum
więcej podobnych podstron