Wstęp do programowania

wykład 3

Agata Półrola

Wydział Matematyki i Informatyki UŁ

sem. zimowy 2012/2013

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Typy modularne

Opis typu

Ada pozwala definiować “cykliczne” typy całkowite (bez znaku).
Definicja typu:

type nazwa typu is mod N;

gdzie N jest liczbą całkowitą dodatnią.

Przykład

type godzina is mod 24;

Wszystkie operacje arytmetyczne na danym typie są wykonywane
modulo N. Zakres typu obejmuje wartości całkowite od 0 do
N − 1.
Standardowy pakiet Interfaces zawiera definicje kilku typów
modularnych (dla N będących potęgami dwójki).

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Operaje wejścia/wyjścia

Operacje wejścia/wyjścia dla typu modularnego T uzyskujemy
konkretyzując dla niego pakiet

ada.text io.modular io

Przykład

with ada.text_io; use ada.text_io;
procedure w03_mod is

type godzina is mod 24;
package xx is new ada.text_io.modular_io(godzina);
use xx;

begin

....

Do wypisywania liczb służy procedura

put

, do ich pobierania

procedura

get

z uzyskanego pakietu.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (Typy modularne)

w i t h ada . T e x t I O ;

u s e

ada . T e x t I O ;

p r o c e d u r e w03 mod i s

t y p e g o d z i n a

i s mod 2 4 ;

p a c k a g e x x

i s new ada . t e x t i o . m o d u l a r i o ( g o d z i n a ) ;

u s e x x ;

d :

g o d z i n a : = 1 0 ;

d1 :

g o d z i n a : = 2 3 ; d2 :

g o d z i n a ;

b e g i n

p u t l i n e ( ” o p e r a c j e

a r y t m e t y c z n e ( n i e k o n i e c z n i e

s e n s o w n e ) : ” ) ;

p u t ( d1 ) ;

p u t ( ’+ ’ ) ;

p u t ( d ) ;

p u t ( ”=” ) ;

d2 := d1+d ;

p u t ( d2 ) ;

n e w l i n e ;

p u t ( d1 ) ;

p u t ( ’ ∗ ’ ) ;

p u t ( d ) ;

p u t ( ”=” ) ;

d2 := d1 ∗ d ;

p u t ( d2 ) ;

s k i p l i n e ;

p u t l i n e ( ” O d l i c z a m y

k o l e j n e

g o d z i n y od

1 0 : 0 0 . . . . ” ) ;

f o r

i

i n

1 . . 1 8

l o o p

p u t ( d ) ; d := d +1; n e w l i n e ; end l o o p ;

end w03 mod ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Konwersja typów

Konwersja z typu całkowitego ze znakiem Tc do typu modularnego
Tm może być wykonana:

za pomocą operacji Tm(wartość typu Tc) - w przypadku
gdy konwertowana wartość będzie poza zakresem typu Tm
dostaniemy błąd

za pomocą operacji

Tm’mod(wartość typu Tc)

, która nie

spowoduje błędu przekroczenia zakresu

Przykład

liczba_godzin_od_polnocy: integer := 134;
g: godzina;
...
g := godzina’mod(liczba_godzin_od_polnocy);

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (Typy modularne - cd)

w i t h ada . T e x t I O ,

ada . I n t e g e r T e x t I O ;

u s e

ada . T e x t I O ,

ada . I n t e g e r T e x t I O ;

p r o c e d u r e w03 mod 2

i s

t y p e g o d z i n a

i s mod 2 4 ;

p a c k a g e x x

i s new ada . t e x t i o . m o d u l a r i o ( g o d z i n a ) ;

u s e x x ;

i l e :

i n t e g e r ;

d :

g o d z i n a ;

b e g i n

p u t ( ” p o d a j

l i c z b e : ” ) ;

g e t ( i l e ) ;

p u t ( ” j e s l i

t y l e

g o d z i n

u p l y n i e od p o l n o c y ,

b e d z i e

g o d z i n a ” ) ;

d := g o d z i n a ’ mod ( i l e ) ;

p u t ( d ) ;

n e w l i n e ( 2 ) ;

p u t ( ” p o d a j

b i e z a c a

g o d z i n e

( p e l n a , w f o r m a c i e GG ) : ” ) ;

g e t ( d ) ;

p u t ( ” z a

i l e

g o d z i n ? . . .

p o d a j :

z a ” ) ;

g e t ( i l e ) ;

p u t ( ” w t e d y b e d z i e

g o d z i n a ” ) ;

d := d + g o d z i n a ’ mod ( i l e ) ;

p u t ( d ) ;

end w03 mod 2 ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Typy stałoprzecinkowe

W Adzie są dwa rodzaje typów stałoprzecinkowych: typy
stałoprzecinowe

zwykłe

i typy stałoprzecinkowe

dziesiętne

.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Typy stałoprzecinkowe zwykłe

Zwykłe typy stałoprzecinkowe są używane w bardzo szczególnych
przypadkach, np. do obliczeń przybliżonych na maszynach nie
mających możliwości wykonywania obliczeń zmiennoprzecinkowych.
Definicja typu:

type T is delta D range P..K;

gdzie D jest dokładnością, a P i K wyznaczają zakres typu.
Wszystkie trzy wartości muszą być liczbami rzeczywistymi.

Przykład

type T is delta 0.1 range -1.0..1.0;

Implementacja Ady wybiera

T’small

będący potęgą dwójki bliską

D; rzeczywisty “krok” między wartościami w typie to T’small

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Operacje wejścia/wyjścia

Operacje wejścia/wyjścia dla zwykłego typu stałoprzecinkowego
uzyskujemy konkretyzując pakiet

ada.text io.fixed io

Przykład

with ada.txt_io; use ada.text_io;
procedure w03_fixord is

type T is delta 0.3 range 1.0..10.0;
package xyz is new ada.text_io.fixed_io(T);
use xyz;

begin

...

Do wypisywania i pobierania liczb służą odpowiednio procedury

put

i

get

z otrzymanego pakietu

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (Typ stałoprzecinkowy zwykły)

w i t h ada . T e x t I O , ada . f l o a t t e x t i o ;
u s e ada . t e x t i o , ada . f l o a t t e x t i o ;

p r o c e d u r e

w 0 3 f i x o r d

i s

t y p e T i s

d e l t a

0 . 5 r a n g e

1 . 0 . . 4 . 0 ;

p a c k a g e x y z

i s new ada . t e x t i o . f i x e d i o (T ) ;

u s e x y z ;

a : T ;

b e g i n

p u t ( ” p r a w d z i w y

’ k r o k ’

t o ” ) ;

p u t ( f l o a t (T ’ s m a l l ) , e x p =>0, a f t = >10); n e w l i n e ;
p u t ( ” p o d a j

l i c z b e

z

p r z e d z i a l u

[ 1 , 4 ]

> ” ) ;

g e t ( a ) ;

p u t ( ” p o d a n a

l i c z b a

: ” ) ;

p u t ( a ) ;

n e w l i n e ;

p u t ( ” w s z y s t k i e

l i c z b y w t y p i e : ” ) ;

n e w l i n e ;

a :=T ’ f i r s t ;

l o o p

p u t ( a , a f t =>4); n e w l i n e ;

i f

a<T ’ l a s t

t h e n a :=T ’ s u c c ( a ) ;

e l s e

e x i t ; end

i f ;

end l o o p ;

end w 0 3 f i x o r d ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Typy stałoprzecinkowe dziesiętne

Typy stałoprzecinkowe dziesiętne są podobne do zwykłych, ale
delta (D) musi być potęgą 10, dodatkowo określa się liczbę
znaczących cyfr dziesiętnych. (N)
Definicja typu:

type T is delta D digits N;

Przykład

type Money is delta 0.01 digits 14;
Tak zdefiniowany typ pozwala reprezentować wartości do tryliona,
z dokładnością 0.01.

Przyjmując że to waluta - mamy 12 cyfr na złotówki i 2 na grosze

Typy tego rodzaju mogą być używane np. w zastosowaniach z
zakresu księgowości.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Operacje wejścia/wyjścia

Operacje wejścia/wyjścia dla typu stałoprzecinkowego dziesiętnego
uzyskujemy konkretyzując dla niego pakiet

ada.text io.decimal io

Przykład

with ada.text_io; use ada.text_io;
procedure w03_fixdec is

type M is delta 0.01 digits 10;
package xyz is new ada.text_io.decimal_io(M);
use xyz;

...

begin

...

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (Typ stałoprzecinkowy dziesiętny)

w i t h ada . T e x t I O ;

u s e ada . t e x t i o ;

p r o c e d u r e

w 0 3 f i x d e c

i s

t y p e M i s

d e l t a

0 . 0 1

d i g i t s

1 0 ;

p a c k a g e x y z

i s new ada . t e x t i o . d e c i m a l i o (M) ;

u s e x y z ;

a :M;

b e g i n

a :=M’ f i r s t ;

l o o p

p u t ( a , a f t = >15); n e w l i n e ;

i f

a<M’ l a s t

t h e n

a :=M’ s u c c ( a ) ;

−− a l t e r n a t y w n i e : a := a+M’ s m a l l ;

s k i p l i n e ;

e l s e

e x i t ; end

i f ;

end l o o p ;

end w 0 3 f i x d e c ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Inne typy liczbowe definiowane przez użytkownika

Jak zdefiniować

Ada pozwala na definiowanie własnych typów liczbowych
“pochodzących” od typów zdefiniowanych wcześniej. Nowy typ
zazwyczaj obejmuje pewien podzakres typu bazowego. Definiujemy
go wtedy:

type nazwa typu is new typ bazowy range zakres;

Przykłady

type ocena is new integer range 0..6;
type NieujFloat is new float range 0.0..float’last;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Konsekwencje

Zdefiniowane w powyższy sposób typy liczbowe są

odrębnymi

typami

.

nie można łączyć ich w jednym wyrażeniu z wartościami ich
typu “bazowego” (np. ocena z integer)

łączenie jest możliwe dopiero po zastosowaniu konwersji typów

aby uzyskać operacje wejścia/wyjścia dla takiego typu, należy
skonkretyzować dla niego odpowiedni pakiet
(ada.text io.integer io albo ada.text io.float io)

Kiedy stosować?

Stosowanie takich typów ma sens gdy chcemy uniknąć omyłkowego
“mieszania” wartości pewnego rodzaju z innymi (czyli gdy
naprawdę chcemy mieć odrębny typ)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (Nowe typy)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . F l o a t T e x t I O ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . F l o a t T e x t I O ;

p r o c e d u r e w 0 3 n o w e t y p y

i s

t y p e o c e n a

i s new i n t e g e r

r a n g e

2 . . 5 ;

p a c k a g e

o c e n a i o

i s new ada . t e x t i o . i n t e g e r i o ( o c e n a ) ;

o , o1 , o2 :

o c e n a ;

s r e d n i a :

f l o a t ;

b : i n t e g e r ;

b e g i n

p u t ( ” p o d a j d w i e o c e n y ( 2 − 5 ) : ” ) ;

o c e n a i o . g e t ( o1 ) ;

o c e n a i o . g e t ( o2 ) ;

o : = ( o1+o2 ) / 2 ;

p u t ( ” s r e d n i a

o c e n a t o : ” ) ;

o c e n a i o . p u t ( o ) ;

n e w l i n e ;

p u t ( ” p r a w d z i w a

s r e d n i a

o c e n t o ” ) ;

s r e d n i a := f l o a t ( o1+o2 ) / 2 . 0 ;

p u t ( s r e d n i a ,

e x p =>0); n e w l i n e ;

p u t ( ” suma o c e n t o

” ) ;

b := i n t e g e r ( o1)+ i n t e g e r ( o2 ) ;

p u t ( b ) ;

n e w l i n e ;

p u t ( ” o c e n a b e d a c a suma t o ” ) ; o := o1+o2 ;

o c e n a i o . p u t ( o ) ;

end w 0 3 n o w e t y p y ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Podtypy

Jak i kiedy definiować

Jeśli nie potrzebujemy odrębnego typu, a jedynie chcemy
ograniczyć zakres możliwych wartości dla pewnych zmiennych,
możemy zdefiniować

podtyp

.

Przykłady

subtype calkowite do 10 is integer range 0..10;
subtype nieuj float is float range 0.0..float’last;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Konskwencje

Zdefiniowane w ten sposób podtypy

nie są odrębnymi typami

można łączyć je w jednym wyrażeniu z wartościami typu
bazowego

operacje wejścia/wyjścia dla podtypu są realizowane przez
odpowiednie procedury dla typu bazowego

ale:

jeśli mamy zmienną danego podtypu, to nie może ona

przyjąc wartości przekraczającej zakres tego podtypu (błąd
przekroczenia zakresu - constraint error)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (Podtypy)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . F l o a t T e x t I O ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . F l o a t T e x t I O ;

p r o c e d u r e w 0 3 p o d t y p y 1

i s

s u b t y p e o c e n a

i s

i n t e g e r

r a n g e

2 . . 5 ;

o , o1 , o2 :

o c e n a ;

s r e d n i a :

f l o a t ;

b : i n t e g e r ;

b e g i n

p u t ( ” p o d a j d w i e o c e n y ( 2 − 5 ) : ” ) ;
ada . i n t e g e r t e x t i o . g e t ( o1 ) ;

g e t ( o2 ) ;

o : = ( o1+o2 ) / 2 ;

p u t ( ” s r e d n i a

o c e n a t o : ” ) ;

p u t ( o ) ;

n e w l i n e ;

p u t ( ” p r a w d z i w a

s r e d n i a

o c e n t o ” ) ;

s r e d n i a := f l o a t ( o1+o2 ) / 2 . 0 ;

p u t ( s r e d n i a ,

e x p =>0); n e w l i n e ;

p u t ( ” suma o c e n t o

” ) ;

b := o1+o2 ;

p u t ( b ) ;

n e w l i n e ;

p u t ( ” o c e n a b e d a c a suma t o ” ) ; o := o1+o2 ;

p u t ( o ) ;

end w 0 3 p o d t y p y 1 ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Predfiniowane podtypy całkowite

Podtypów obejmujących pewne często używane zakresy możemy
nie definiować - są dostępne w języku (predefiniowane):

podtyp

positive

- liczby całkowite dodatnie (integer

range 1..integer’last)

podtyp

natural

- liczby całkowite nieujemne (integer

range 0..integer’last)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Trochę matematyki

Stałe matematyczne

Ada zawiera pakiet

ada.numerics

, w którym zdefiniowane są

wartości stałych e i π

stała e to

ada.numerics.e

stała pi to

ada.numerics.pi

Obie wartości są typu universal real.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (Jak uzyskać π i e)

w i t h ada . t e x t i o ,

ada . f l o a t t e x t i o ,

ada . n u m e r i c s ;

u s e ada . t e x t i o ,

ada . f l o a t t e x t i o ;

p r o c e d u r e

w 0 3 s t a l e m a t

i s

b e g i n

p u t ( ” s t a l a

p i

w y n o s i ” ) ;

p u t ( ada . n u m e r i c s . p i ,

e x p =>0, a f t = >20);

n e w l i n e ;

p u t ( ” s t a l a

e w y n o s i ” ) ;

p u t ( ada . n u m e r i c s . e ,

e x p =>0, a f t = >20);

end w 0 3 s t a l e m a t ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Funkcje matematyczne

Czasami w programie potrzebujemy bardziej zaawansowanych
funkcji matematycznych. Funkcje dla typu float są udostępniane
przez pakiet

ada.numerics.elementary functions

.

Dostępne funkcje:

sqrt (sqrt(x) -

√

x , x typu float)

log (log(x) to ln(x ), log(x,a) to log

a

(x ))

exp (exp(x) to e

x

)

** - potęgowanie o wykładniku rzeczywistym

sin, cos, tan, cot, arcsin, arccos, arctan,
arccot, sinh, cosh, tanh, coth, arcsinh, arccosh,
arctanh, arccoth

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (Funkcje matematyczne)

w i t h ada . t e x t i o ,

ada . f l o a t t e x t i o ,

ada . n u m e r i c s . e l e m e n t a r y f u n c t i o n s ;

u s e ada . t e x t i o ,

ada . f l o a t t e x t i o ,

ada . n u m e r i c s . e l e m e n t a r y f u n c t i o n s ;

p r o c e d u r e w03 mat

i s

b e g i n

p u t ( ” p u t 2 ˆ { 1 / 2 } t o ” ) ;

s e t c o l ( 2 0 ) ;

p u t ( 2 . 0 ∗ ∗ 0 . 5 ,

e x p =>0, a f t = >10); n e w l i n e ;

p u t ( ” p i e r w i a s t e k

z 2 t o ” ) ;

s e t c o l ( 2 0 ) ;

p u t ( s q r t ( 2 . 0 ) ,

e x p =>0, a f t = >10);

end w03 mat ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Pakiet ada.numerics.elementary functions jest konkretyzacją
pakietu rodzajowego

ada.numerics.generic elementary functions

dla typu

float. Jeśli potrzebujemy funkcji matematycznych dla innego
typu rzeczywistego, musimy sami dokonać odpowiedniej
konkretyzacji tego pakietu

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (Funkcje matematyczne, typ long float)

w i t h ada . t e x t i o ,

ada . l o n g f l o a t t e x t i o ,

ada . n u m e r i c s . g e n e r i c e l e m e n t a r y f u n c t i o n s ;

u s e ada . t e x t i o ,

ada . l o n g f l o a t t e x t i o ;

p r o c e d u r e

w 0 3 m a t l f

i s

p a c k a g e f 1

i s new

ada . N u m e r i c s . g e n e r i c e l e m e n t a r y f u n c t i o n s ( l o n g f l o a t ) ;

u s e f 1 ;

b e g i n

p u t ( ” p u t 2 2 2 2 2 2 2 2 2 2 2 2 2 2 ˆ { 1 / 2 } t o ” ) ;

s e t c o l ( 4 0 ) ;

p u t ( 2 2 2 2 2 2 2 2 2 2 2 2 2 2 . 0 ∗ ∗ 0 . 5 , e x p =>0, a f t = >10); n e w l i n e ;
p u t ( ” p i e r w i a s t e k

z 2 2 2 2 2 2 2 2 2 2 2 2 2 2 t o ” ) ;

s e t c o l ( 4 0 ) ;

p u t ( s q r t ( 2 2 2 2 2 2 2 2 2 2 2 2 2 2 . 0 ) , e x p =>0, a f t = >10);

end w 0 3 m a t l f ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Instrukcja warunkowa

W programie używamy

instrukcji sterujących

, umożliwiających

warunkowe lub iteracyjne wykonanie pewnych fragmentów kodu
Jedną z instrukcji sterujących jest

instrukcja warunkowa

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Instrukcja warunkowa

Instrukcja warunkowa występuje zazwyczaj w trzech wersjach:

jeżeli warunek to instrukcje_do_wykonania

jeżeli warunek to

instrukcje_do_wykonania_1

w_przeciwnym_razie

instrukcje_do_wykonania_2

jeżeli warunek1 to

instrukcje_do_wykonania1

jeżeli warunek2 to

instrukcje_do_wykonania_2

...
w_pozostałych_przypadkach

instrukcje_do_wykonania_n

Instrukcja daje możliwość wyboru jednego z dostępnych wariantów,

zależnie od wartości logicznej warunku

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Instrukcja warunkowa w Adzie

if warunek then

instrukcje_do_wykonania

end if;
---------------------------------------

if warunek then

instrukcje_do_wykonania_1

else

instrukcje_do_wykonania_2

end if;
-------------------------------------

if warunek1 then

instrukcje_do_wykonania1

elsif warunek2 then

instrukcje_do_wykonania_2

...
else

instrukcje_do_wykonania_n

end if;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Jak skonstruować warunek

Porównywanie liczb

Liczby możemy ze sobą porównywać. Operatory porównywania to

< > <= >= = /=

Wyrażenie zawierające operator porównywania jest

wyrażeniem logicznym

- ma wartość prawdy lub fałszu (

true

lub

false

)

Przy porównywaniu nie wolno mieszać typów liczbowych (tak
jak w wyrażeniach arytmetycznych)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

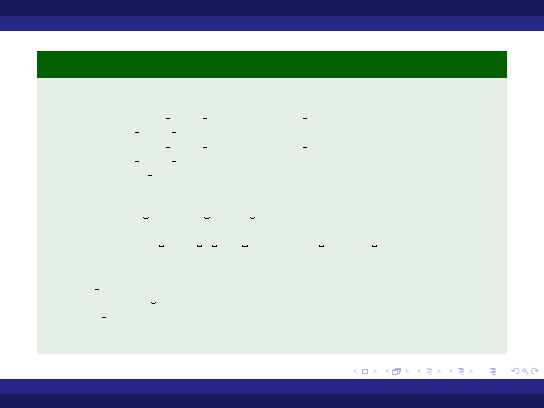
Przykład (Instukcja warunkowa - wersja 1)

w i t h ada . i n t e g e r t e x t i o ,

ada . t e x t i o ,

ada . f l o a t t e x t i o ,

ada . n u m e r i c s ;

u s e

ada . i n t e g e r t e x t i o ,

ada . t e x t i o ,

ada . f l o a t t e x t i o ,

ada . n u m e r i c s ;

p r o c e d u r e

w 0 3 i f 1

i s

r :

i n t e g e r ;

b e g i n

p u t ( ” p o d a j p r o m i e n

k o l a : ” ) ;

g e t ( r ) ;

i f

r >0 t h e n
p u t ( ” p o l e

k o l a o tym p r o m i e n i u

w y n o s i ” ) ;

p u t ( ada . n u m e r i c s . p i ∗

f l o a t ( r ∗ ∗ 2 ) , e x p =>0);

end

i f ;

n e w l i n e ;

p u t ( ” k o n i e c ” ) ;

end w 0 3 i f 1 ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

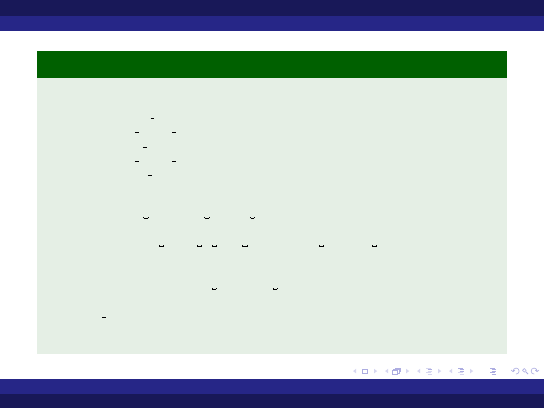
Przykład (Instrukcja warunkowa - wersja 2)

w i t h

ada . t e x t i o ,

ada . f l o a t t e x t i o ,

ada . n u m e r i c s ;

u s e

ada . t e x t i o ,

ada . f l o a t t e x t i o ,

ada . n u m e r i c s ;

p r o c e d u r e

w 0 3 i f 2

i s

r :

f l o a t ;

b e g i n

p u t ( ” p o d a j p r o m i e n

k o l a : ” ) ;

g e t ( r ) ;

i f

r >0.0 t h e n

−− w a r u n e k b e z ” m i e s z a n i a ” typow !

p u t ( ” p o l e

k o l a o tym p r o m i e n i u

w y n o s i ” ) ;

p u t ( ada . n u m e r i c s . p i ∗

f l o a t ( r ∗ ∗ 2 ) , e x p =>0);

e l s e

p u t ( ” n i e p o p r a w n a

w a r t o s c

! ” ) ;

end

i f ;

end w 0 3 i f 2 ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

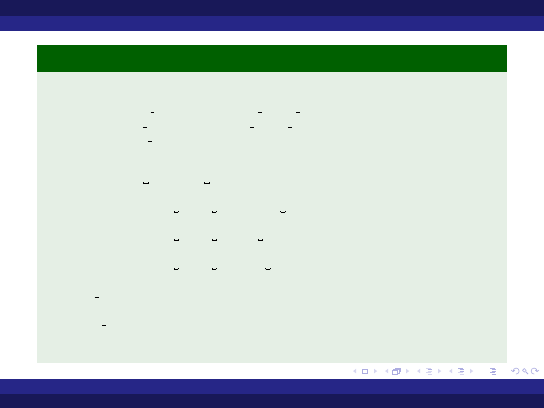
Przykład (Instrukcja warunkowa - wersja 3)

w i t h

ada . t e x t i o ,

ada . f l o a t t e x t i o ;

u s e

ada . t e x t i o ,

ada . f l o a t t e x t i o ;

p r o c e d u r e

w 0 3 i f 3

i s

a :

f l o a t ;

b e g i n

p u t ( ” p o d a j

l i c z b e : ” ) ;

g e t ( a ) ;

i f

a >0.0 t h e n

p u t ( ” l i c z b a

b y l a

d o d a t n i a ” ) ;

e l s i f

a =0.0 t h e n

p u t ( ” l i c z b a

b y l a z e r e m ” ) ;

e l s e

p u t ( ” l i c z b a

b y l a uj emn a ” ) ;

end

i f ;

n e w l i n e ;

p u t ( ” k o n i e c ” ) ;

end w 0 3 i f 3 ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Spójniki logiczne

Dostępne operatory logiczne to and, or, not, xor, and then i or
else,

W1 and W2, W1 or W2 -

zawsze

oblicza się wartość logiczną

obu warunków (W1 i W2)

W1 and then W2, W1 or else W2 - wartość logiczną W2
oblicza się tylko gdy potrzeba (tj. gdy obliczenie W1 nie mówi
nic o ostatecznym wyniku), czyli

w przypadku and then - gdy W1 jest prawdziwy
w przypadku or else - gdy W1 jest fałszywy

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Spójniki logiczne

Dostępne operatory logiczne to and, or, not, xor, and then i or
else,

W1 and W2, W1 or W2 -

zawsze

oblicza się wartość logiczną

obu warunków (W1 i W2)

W1 and then W2, W1 or else W2 - wartość logiczną W2
oblicza się tylko gdy potrzeba (tj. gdy obliczenie W1 nie mówi
nic o ostatecznym wyniku), czyli

w przypadku and then - gdy W1 jest prawdziwy
w przypadku or else - gdy W1 jest fałszywy

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (Spójnik and then)

w i t h

ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

u s e

ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

p r o c e d u r e

w 0 3 i f 4

i s

a , b :

i n t e g e r ;

b e g i n

p u t ( ” p o d a j d w i e

l i c z b y : ” ) ;

g e t ( a ) ;

g e t ( b ) ;

i f

b/=0

and t h e n a /b>1 t h e n

p u t ( ” i l o r a z

t y c h

l i c z b

j e s t

w i e k s z y od 1 ” ) ;

end

i f ;

end w 0 3 i f 4 ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania