
Automatyka i sterowanie
Krzysztof Marzjan
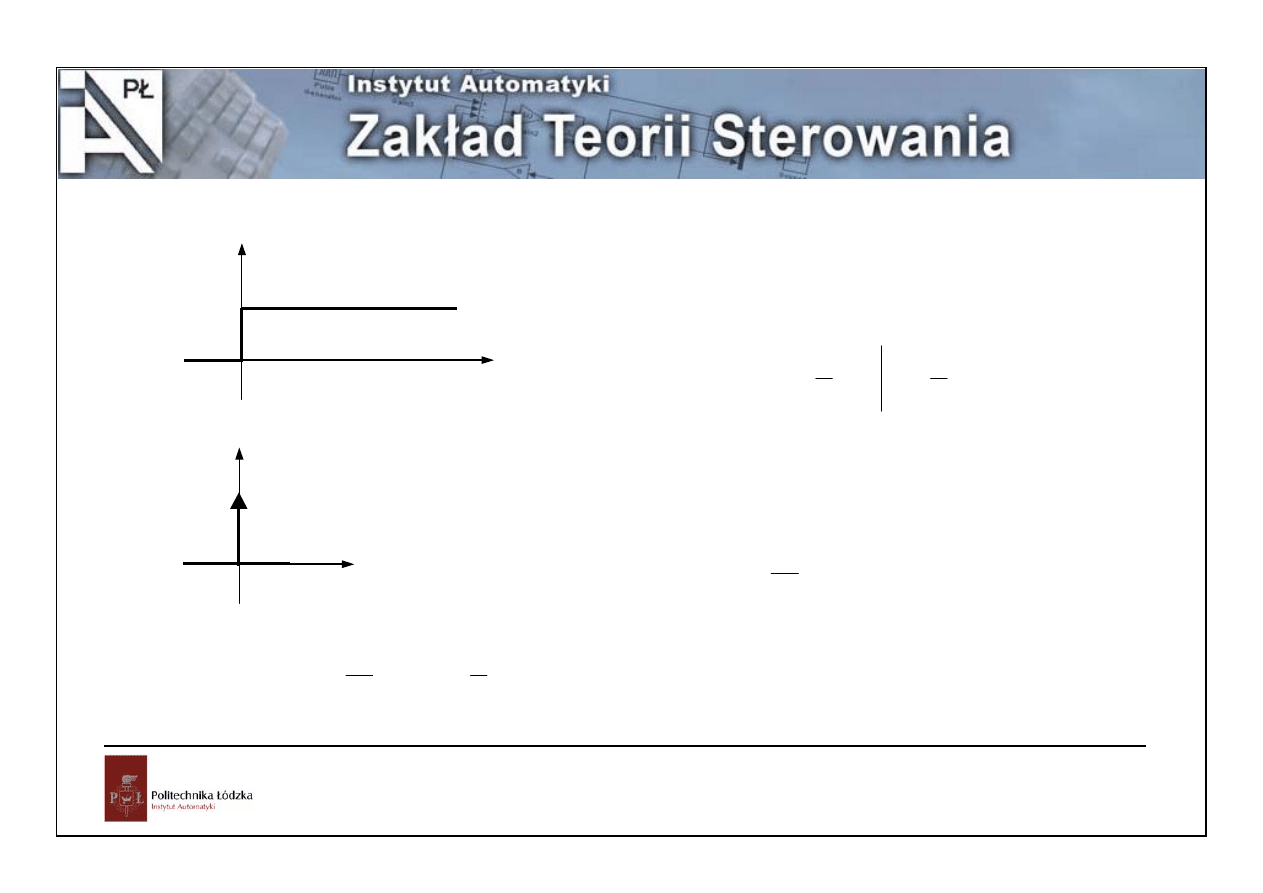
1. Znaleźć transformatę Laplace’a funkcji jednostkowej
f(t)
t
1
⎩
⎨
⎧
≥
<
=
=
0
1
0
0
)
(
1
)
(
t
t
t
t
f
Z definicji przekształcenia otrzymuje się:
( )
s
e
s
dt
e
s
F
st
st
1
1
1
0
0
=
−
=
⋅
=
∞
∞
−
−
∫
2. Znaleźć transformatę Laplace’a impulsu Diraca
)
(t
δ
f(t)
t
( )
( )
∫
∞
∞
−
=
⎩
⎨
⎧
=
∞
≠
=
1
0
0
0
dt
t
t
t
t
δ
δ
( )
( )
( ) ( )
t
t
dt
d
t
d
t
δ
τ
τ
δ
=
=
∫
∞
−
1
1
Wykorzystując twierdzenie o transformacie pochodnej można zapisać:
2
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
{
}
1
1
)
(
1
)
(
)
(
=
=
⎭
⎬
⎫
⎩
⎨
⎧
=
=
s
s
t
dt
d
L
t
L
s
F
δ

3. Znaleźć transformatę Laplace’a przesuniętej funkcji skokowej
f(t)
t
A
τ
⎩
⎨
⎧
<
≥
=
−
⋅
=
τ
τ
τ
t
t
A
t
A
t
f
0
)
(
1
)
(
Można wykorzystać definicję transformaty:
(
)
τ
τ
τ
τ
s
st
st
st
e
s
A
e
s
A
dt
e
A
dt
e
t
A
s
F
−
∞
∞
∞
−
−
−
=
−
=
=
−
⋅
=
∫
∫
0
1
)
(
ale
także twierdzenie o opóźnieniu, wiadomo, że
{ }
s
t
L
1
)
(
1
=
, stąd
3
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
{
}
τ
τ
s
e
s
A
t
A
L
s
F
−
=
−
⋅
=
)
(
1
)
(

4. Znaleźć transformatę Laplace’a impulsu prostokątnego
f(t)
t
A
τ
-A
)
(
1 t
A
⋅
)
(
1
τ
−
⋅
−
t
A
f(t)
t
A
τ
[
]
)
(
1
)
(
1
)
(
τ
−
−
=
t
t
A
t
f
{
}
[
]
{
}
{
} {
}
s
e
A
e
s
s
A
t
L
t
L
A
t
t
A
L
t
f
L
s
F
s
s
)
1
(
1
1
]
)
(
1
)
(
1
[
)
(
1
)
(
1
)
(
)
(
τ
τ
τ
τ
−
−
−
=
⎥⎦
⎤
⎢⎣
⎡ −
=
−
−
=
−
−
=
=
Transformatę tę można także wyznaczyć korzystając z definicji przekształcenia:
4
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
s
e
A
e
s
A
dt
e
A
dt
e
t
f
s
F
s
st
st
st
)
1
(
)
(
)
(
0
0
0
τ
τ
τ
−
−
−
∞
−
−
=
−
=
=
=
∫
∫

5. Znaleźć transformatę Laplace’a ciągu impulsów prostokątnych
f(t)
t
A
τ
T
Transformata pojedynczego impulsu prostokątnego
została obliczona w przykładzie poprzednim, wobec
tego:
s
e
A
s
F
s
T
)
1
(
)
(
τ
−
−
=
;
Korzystając ze wzoru na transformatę funkcji
okresowej otrzymuje się:
( )
)
1
(
)
1
(
sT
s
e
s
e
A
s
f
−
−
−
−
=
τ
5
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady

6. Obliczyć transformatę funkcji liniowej
)
(
1
)
(
t
t
t
f
⋅
=
W tym przypadku można skorzystać z twierdzenia o różniczkowaniu w dziedzinie zmiennej zespolonej
{
} ( )
2
2
1
1
1
1
1
)
(
1
s
s
s
ds
d
t
t
L
=
⎟
⎠
⎞
⎜
⎝
⎛−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
⋅
7. Znaleźć transformatę Laplace’a funkcji
)
2
(
1
)
3
2
(
)
(
−
⋅
−
=
t
t
t
f
.
Aby
wyznaczyć transformatę podanej funkcji należy ją przekształcić
)
2
(
1
)
2
(
1
)
2
(
2
)
2
(
1
]
1
)
2
[(
2
)
2
(
1
)
3
2
(
)
(
−
+
−
⋅
−
=
−
⋅
+
−
=
−
⋅
−
=
t
t
t
t
t
t
t
t
f
Należy zwrócić uwagę na to, by argument funkcji, której transformatę się wyznacza był identyczny jak argument
skoku jednostkowego, stąd:
{
6
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
}
s
s
s
e
s
s
e
s
e
s
t
t
t
L
s
F
2
2
2
2
2
2
1
2
)
2
(
1
)
2
(
1
)
2
(
2
)
(
−
−
−
+
=
+
=
−
+
−
⋅
−
=

8. Znaleźć transformatę Laplace’a funkcji, której przebieg pokazuje rysunek
Przedstawiony przebieg daje się rozłożyć na przebiegi opisane funkcjami, których transformaty można w prosty
sposób wyznaczyć:
f(t)
t
A
τ
)
(
1 t
t
A ⋅
τ
)
(
1
)
(
τ
τ
τ
−
⋅
−
−
t
t
A
f(t)
t
τ
)
1
(
1
1
)
(
1
)
(
)
(
1
)
(
2
2
2
τ
τ
τ
τ
τ
τ
τ
τ
s
s
e
s
A
e
s
s
A
t
t
A
t
t
A
L
s
F
−
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
⎭
⎬
⎫
⎩
⎨
⎧
−
⋅
−
−
⋅
=
;
7
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
W obliczeniach wykorzystano twierdzenie o opóźnieniu.

9. Obliczyć transformatę funkcji wykładniczej
)
(
1
)
(
t
e
t
f
at
⋅
=
−
Aby obliczyć transformatę tej funkcji możemy skorzystać z twierdzenia o przesunięciu w dziedzinie zmiennej
zespolonej
{
}
a
s
t
e
L
at
+
=
⋅
−
1
)
(
1
10. Znaleźć transformatę Laplace’a funkcji
.
)
2
(
1
)
(
)
2
3
(
−
⋅
=
−
−
t
e
t
f
t
)
2
(
1
)
2
(
1
)
2
(
1
)
(
)
2
(
3
4
4
)
2
(
3
)
2
3
(
−
⋅
⋅
=
−
⋅
=
−
⋅
=
−
−
−
−
−
−
−
−
t
e
e
t
e
t
e
t
f
t
t
t
8
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
{
}
3
3
1
)
2
(
1
)
(
)
2
(
2
2
4
)
2
(
3
4
+
=
+
=
−
⋅
⋅
=
+
−
−
−
−
−
−
s
e
e
s
e
t
e
e
L
s
F
s
s
t

11. Obliczyć transformatę funkcji
)
(
1
sin
)
(
t
t
t
f
⋅
=
ω
Najprościej transformatę tę obliczyć, zapisując daną funkcję następująco:
)
(
1
2
)
(
1
sin
)
(
t
j
e
e
t
t
t
f
t
j
t
j
⋅
−
=
⋅
=
−
ω
ω
ω
( )
2
2
2
2
2
1
1
1
2
1
1
2
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
=
+
+
−
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
−
=
⎭
⎬
⎫
⎩
⎨
⎧
⋅
−
−
s
s
j
s
j
s
j
j
s
j
s
j
t
j
e
e
L
t
j
t
j
12. Obliczyć transformatę Laplace’a funkcji
)
2
(
1
4
sin
)
(
−
⋅
=
t
t
t
f
.
)
2
(
1
)
2
(
4
cos
8
sin
)
2
(
1
)
2
(
4
sin
8
cos
)
2
(
1
]
8
sin
)
2
(
4
cos
8
cos
)
2
(
4
[sin
)
2
(
1
]
8
)
2
(
4
sin[
)
2
(
1
4
sin
)
(
−
⋅
−
⋅
+
−
⋅
−
⋅
=
=
−
⋅
⋅
−
+
⋅
−
=
−
⋅
+
−
=
−
⋅
=
t
t
t
t
t
t
t
t
t
t
t
t
f
9
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
{
}
s
s
e
s
s
e
s
t
t
t
t
L
s
F
2
2
2
2
2
2
4
8
sin
4
4
8
cos
)
2
(
1
)
2
(
4
cos
8
sin
)
2
(
1
)
2
(
4
sin
8
cos
)
(
−
−
+
+
+
=
=
−
⋅
−
⋅
+
−
⋅
−
⋅
=

13. Znaleźć transformatę funkcji, której przebieg przedstawia rysunek
f(t)
t
1
ω
π
⎪
⎪
⎪
⎩
⎪⎪
⎪
⎨
⎧
>
≤
≤
<
=
ω
π
ω
π
ω
t
t
t
t
t
f
0
0
sin
0
0
)
(
ω
π
⎟
⎠
⎞
⎜
⎝
⎛ −
⋅
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛ −
ω
π
ω
π
ω
t
t
1
sin
f(t)
t
1
-1
)
(
1
sin
t
t
⋅
ω
⎟
⎠
⎞
⎜
⎝
⎛ −
⋅
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛ −
+
⋅
=
ω
π
ω
π
ω
ω
t
t
t
t
t
f
1
sin
)
(
1
sin
)
(
10
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
2
2
2
2
2
2
1
1
sin
)
(
1
sin
)
(
ω
ω
ω
ω
ω
ω
ω
π
ω
π
ω
ω
ω
π
ω
π
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
=
+
+
+
==
⎭
⎬
⎫
⎩
⎨
⎧
⎟
⎠
⎞
⎜
⎝
⎛ −
⋅
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛ −
+
⋅
=
−
−
s
e
e
s
s
t
t
t
t
L
s
F
s
s

14. Znaleźć transformatę Laplace’a funkcji, której przebieg pokazuje rysunek
11
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
2A
A
t
0
2t
0
3t
0
0
t
f(t)

Przedstawiony przebieg daje się rozłożyć na przebiegi opisane funkcjami, których transformaty można w prosty
sposób wyznaczyć:
12
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
t
0
-A
-2A
2A
A
2t
0
3t
0
0
f(t)
)
2
(
1
)
2
(
2
0
0
0
t
t
t
t
t
A
−
⋅
−
−
)
(
1
)
(
0
0
0
t
t
t
t
t
A
−
⋅
−
)
(
1 t
A
⋅
)
3
(
1
0
t
t
A
−
⋅
−
)
3
(
1
)
3
(
0
0
0
t
t
t
t
t
A
−
⋅
−
t

)
3
(
1
)
3
(
1
)
3
(
)
2
(
1
)
2
(
2
)
(
1
)
(
)
(
1
)
(
0
0
0
0
0
0
0
0
0
0
t
t
A
t
t
t
t
t
A
t
t
t
t
t
A
t
t
t
t
t
A
t
A
t
f
−
⋅
−
−
⋅
−
+
−
⋅
−
−
−
⋅
−
+
⋅
=
13
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
0
0
0
0
3
3
2
0
2
2
0
2
0
2
st
st
st
st
e
s
A
e
s
t
A
e
s
t
A
e
s
t
A
s
A
)
s
(
F
−
−
−
−
−
+
−
+
=

Ćwiczenia do samodzielnego rozwiązania
Oblicz transformatę Laplace’a funkcji:
)
(
1
)
3
2
(
)
(
t
t
t
f
⋅
−
=
a.
b.
)
2
(
1
)
1
3
(
)
(
−
⋅
−
=
t
t
t
f
c.
)
2
(
1
)
(
)
1
(
4
−
⋅
=
−
−
t
e
t
f
t
d.
)
(
1
cos
)
(
t
t
t
f
⋅
=
ω
e.
)
(
1
sin
)
(
t
t
t
f
⋅
=
ω
)
f.
(
1
sinh
)
(
t
t
t
f
⋅
=
ω
)
g.
(
1
cosh
)
(
t
t
t
f
⋅
=
ω
14
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
h.
)
(
1
)
3
(
2
sin
)
(
t
t
t
f
⋅
−
=

Znaleźć transformatę Laplace’a funkcji, której przebieg pokazuje rysunek
a.
2A
A
t
0
2t
0
3t
0
0
t
f(t)
b.
2A
A
t
0
2t
0
3t
0
0
t
f(t)
c.
3
2
4
6
0
t
f(t)
d.
5
1
2
3
0
t
f(t)
15
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady

Znaleźć oryginał funkcji
1.
2
1
)
(
+
+
=
s
s
s
F
Należy zwrócić uwagę na fakt, że gdy transformata jest funkcją wymierną, to musi być ściśle właściwą, stąd:
)
(
1
)
(
2
1
1
2
1
2
2
1
)
(
2
1
1
1
t
e
t
s
L
s
s
L
s
s
L
t
f
t
⋅
−
=
⎭
⎬
⎫
⎩
⎨
⎧
+
−
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
−
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
=
−
−
−
−
δ
16
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
2.
2
4
1
3
)
(
+
+
=
s
s
s
F
)
(
1
8
1
)
(
4
3
2
1
6
1
1
4
3
2
1
3
1
4
3
2
4
1
3
)
(
2
1
1
1
t
e
t
s
L
s
s
L
s
s
L
t
f
t
⋅
−
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
+
−
+
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
+
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
=
−
−
−
−
δ

3.
4
4
1
)
(
2
+
+
=
s
s
s
F
)
(
1
)
2
(
1
4
4
1
)
(
2
2
1
2
1
t
te
s
L
s
s
L
t
f
t
⋅
=
⎭
⎬
⎫
⎩
⎨
⎧
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
=
−
−
−
17
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
4.
13
4
1
)
(
2
+
+
=
s
s
s
F
)
(
1
3
sin
3
1
3
)
2
(
3
3
1
13
4
1
)
(
2
2
2
1
2
1
t
e
t
s
L
s
s
L
t
f
t
⋅
⋅
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
+
+
⋅
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
=
−
−
−

5.
3
4
1
)
(
2
+
+
=
s
s
s
F
t
e
t
s
L
s
s
L
t
f
t
)
(
1
sinh
1
)
2
(
1
3
4
1
)
(
2
2
2
1
2
1
⋅
⋅
=
⎭
⎬
⎫
⎩
⎨
⎧
−
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
=
−
−
−
lub
18
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
)
(
1
2
1
2
1
3
2
1
1
2
1
)
3
(
)
1
(
1
3
4
1
)
(
3
1
1
2
1
t
e
e
s
s
L
s
s
L
s
s
L
t
f
t
t
⋅
⎟
⎠
⎞
⎜
⎝
⎛
−
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
+
−
+
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
=
−
−
−
−
−

19
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
6.
5
2
1
3
)
(
2
2
+
+
+
+
=
s
s
s
s
s
F
)
(
1
2
sin
2
5
2
cos
)
(
2
)
1
(
2
2
5
2
)
1
(
1
1
2
)
1
(
2
2
5
1
1
5
2
4
1
5
2
1
3
)
(
2
2
2
2
1
2
2
1
2
1
2
2
1
t
e
t
t
t
s
s
s
L
s
s
L
s
s
s
L
s
s
s
s
L
t
f
t
⋅
⎟
⎠
⎞
⎜
⎝
⎛
−
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
−
+
+
+
+
=
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
+
+
⋅
−
+
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
−
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
+
+
=
−
−
−
−
−
δ

20
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
7.
1
2
1
3
)
(
2
2
+
+
+
+
=
s
s
s
s
s
F
)
(
1
)
1
(
)
(
)
1
(
1
1
1
1
)
1
(
1
1
1
)
1
(
1
1
2
1
3
)
(
2
1
2
1
2
1
2
2
1
t
e
t
t
s
s
L
s
s
L
s
s
L
s
s
s
s
L
t
f
t
⋅
−
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
−
+
+
=
=
⎭
⎬
⎫
⎩
⎨
⎧
+
−
+
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
+
+
=
−
−
−
−
−
δ

21
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
8.
5
6
1
3
)
(
2
2
+
+
+
+
=
s
s
s
s
s
F
)
(
1
2
sinh
2
5
2
cosh
3
)
(
2
)
3
(
2
2
5
2
)
3
(
3
3
1
2
)
3
(
2
2
5
)
3
(
3
1
5
6
4
3
1
5
6
1
3
)
(
3
2
2
2
2
1
2
2
1
2
1
2
2
1
t
e
t
t
t
s
s
s
L
s
s
L
s
s
s
L
s
s
s
s
L
t
f
t
⋅
⎟
⎠
⎞
⎜
⎝
⎛
+
−
+
=
⎭
⎬
⎫
⎩
⎨
⎧
−
+
+
−
+
+
−
=
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
−
+
⋅
+
+
−
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
−
−
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
+
+
=
−
−
−
−
−
δ

lub
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
+
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
−
−
+
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
+
+
=
−
−
−
5
1
1
)
5
(
)
1
(
4
3
1
5
6
1
3
)
(
2
1
1
1
2
2
1
s
A
s
A
L
s
s
s
L
s
s
s
s
L
t
f
Współczynniki rozkładu na ułamki proste:
4
11
1
4
3
4
1
5
4
3
5
2
1
1
−
=
+
−
−
=
−
=
+
−
−
=
−
=
−
=
s
s
s
s
A
s
s
A
22
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
)
(
1
4
11
4
1
)
(
5
4
11
1
4
1
1
5
1
t
e
e
t
s
s
L
t
t
⋅
⎟
⎠
⎞
⎜
⎝
⎛
−
−
+
=
⎪
⎪
⎭
⎪⎪
⎬
⎫
⎪
⎪
⎩
⎪⎪
⎨
⎧
+
−
+
+
−
+
=
−
−
−
δ

9. Rozwiązać równanie różniczkowe metodą przekształcenia Laplace’a.
0
)
0
(
,
1
)
0
(
0
)
(
13
)
(
4
)
(
2
2
=
′
=
=
+
+
+
+
y
y
t
y
dt
t
dy
dt
t
y
d
Dokonuje się przekształcenia Laplace’a z uwzględnieniem warunków początkowych:
4
)
(
)
13
4
(
0
)
(
13
4
)
(
4
)
(
0
)
(
13
)
0
(
4
)
(
4
)
0
(
)
0
(
)
(
2
2
2
+
=
+
+
=
+
−
+
−
=
+
−
+
′
−
−
+
+
+
s
s
y
s
s
s
y
s
sy
s
s
y
s
s
y
y
s
sy
y
sy
s
y
s
Stąd transformata rozwiązania dana jest zależnością:
2
2
2
2
2
2
2
2
2
2
2
3
)
2
(
3
3
2
3
)
2
(
2
3
)
2
(
2
3
)
2
(
2
3
)
2
(
4
13
4
4
)
(
+
+
+
+
+
+
=
+
+
+
+
+
+
=
+
+
+
=
+
+
+
=
s
s
s
s
s
s
s
s
s
s
s
s
y
I ostatecznie rozwiązanie jest postaci:
23
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
)
(
1
3
sin
3
2
3
cos
)
(
2
t
t
t
e
t
y
t
⋅
⎭
⎬
⎫
⎩
⎨
⎧
⎟
⎠
⎞
⎜
⎝
⎛
+
=
−

10. Rozwiązać równanie różniczkowe metodą przekształcenia Laplace’a.
1
)
(
)
1
(
0
)
(
1
)
(
0
)
(
)
0
(
)
0
(
)
0
(
)
(
1
)
0
(
,
0
)
0
(
,
1
)
0
(
0
)
(
)
(
2
3
2
3
2
3
3
3
+
=
−
=
−
−
−
=
−
′′
−
′
−
−
=
′′
=
′
=
=
−
+
+
+
+
+
+
s
s
y
s
s
y
s
s
y
s
s
y
y
y
s
y
s
s
y
s
y
y
y
t
y
dt
t
y
d
Transformata
rozwiązania jest równa:
)
1
(
)
1
(
1
1
1
)
(
2
2
3
2
+
+
−
+
=
−
+
=
s
s
s
s
s
s
s
y
Transformatę tę można zapisać w postaci sumy dwóch ułamków:
24
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
)
1
(
)
1
(
1
)
1
(
)
1
(
)
1
(
)
(
)
1
(
1
1
)
(
2
2
2
3
2
2
1
2
3
2
1
+
+
−
+
=
+
+
−
−
+
+
+
+
=
+
+
+
+
−
=
s
s
s
s
s
s
s
s
A
s
A
s
s
A
s
s
A
s
A
s
A
s
y

Porównując współczynniki przy tych samych potęgach otrzymuje się układ równań:
⎪
⎩
⎪
⎨
⎧
=
−
+
=
+
−
=
+
1
0
1
3
1
3
2
1
2
1
A
A
A
A
A
A
A
⎪
⎩
⎪
⎨
⎧
+
=
−
=
+
=
+
1
1
2
1
3
1
3
1
2
1
A
A
A
A
A
A
⎪
⎪
⎩
⎪⎪
⎨
⎧
=
−
=
=
+
1
3
2
1
3
1
1
2
1
A
A
A
A
A
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
−
=
−
=
=
3
1
3
2
3
1
3
2
1
A
A
A
Stąd, transformata rozwiązania ma postać:
25
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
1
1
3
1
1
1
3
2
)
(
2
+
+
−
+
−
=
s
s
s
s
s
y

po przekształceniach:
2
2
2
2
2
2
2
3
2
1
2
3
3
3
2
3
2
1
2
1
3
1
1
1
3
2
2
3
2
1
2
3
2
1
3
1
1
1
3
2
)
(
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛ +
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛ +
+
+
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛ +
−
+
+
−
=
s
s
s
s
s
s
s
s
y
i ostatecznie rozwiązanie:
26
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
)
(
1
2
3
sin
3
3
2
3
cos
3
1
3
2
)
(
2
1
2
1
t
t
e
t
e
e
t
y
t
t
t
⋅
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
−
+
=
−
−

11. Rozwiązać równanie różniczkowe metodą przekształcenia Laplace’a.
1
)
0
(
,
1
)
0
(
)
(
1
2
)
(
4
)
(
4
)
(
2
2
−
=
′
=
⋅
=
+
+
+
+
y
y
t
t
y
dt
t
dy
dt
t
y
d
s
s
s
y
s
s
s
s
y
s
sy
s
s
y
s
s
s
y
y
s
sy
y
sy
s
y
s
2
3
)
(
)
4
4
(
2
)
(
4
4
)
(
4
1
)
(
2
)
(
4
)
0
(
4
)
(
4
)
0
(
)
0
(
)
(
2
2
2
+
+
=
+
+
=
+
−
+
+
−
=
+
−
+
′
−
−
+
+
+
Transformata rozwiązania jest równa:
)
4
4
(
2
3
)
(
2
2
+
+
+
+
=
s
s
s
s
s
s
y
27
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
)
4
4
(
2
3
)
4
4
(
)
4
4
(
4
4
)
(
2
2
2
3
2
2
2
1
2
3
2
1
+
+
+
+
=
+
+
+
+
+
+
=
+
+
+
+
=
s
s
s
s
s
s
s
s
s
A
s
A
s
s
A
s
s
A
s
A
s
A
s
y

Porównując współczynniki przy tych samych potęgach otrzymuje się układ równań:
⎪
⎩
⎪
⎨
⎧
=
=
+
=
+
2
4
3
4
1
1
3
1
2
1
A
A
A
A
A
stąd
1
2
1
2
1
3
2
1
=
=
=
A
A
A
Stąd, transformata rozwiązania ma postać:
4
4
2
2
1
1
2
1
)
(
2
+
+
+
+
=
s
s
s
s
s
y
po przekształceniach:
2
1
2
1
1
2
1
)
2
(
2
2
1
1
2
1
)
(
2
+
+
=
+
+
+
=
s
s
s
s
s
s
y
Rozwiązanie jest postaci:
28
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
)
(
1
)
1
(
2
1
)
(
2
t
e
t
y
t
⋅
+
=
−

Ćwiczenia do samodzielnego rozwiązania
1. Znaleźć oryginał funkcji:
a.
3
1
)
(
+
−
=
s
s
s
F
b.
1
4
1
2
)
(
+
−
=
s
s
s
F
c.
3
4
1
)
(
2
2
+
+
+
=
s
s
s
s
F
d.
9
6
1
3
)
(
2
2
+
+
+
+
=
s
s
s
s
s
F
29
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
e.
13
6
1
3
)
(
2
2
+
+
+
+
=
s
s
s
s
s
F

2. Rozwiąż równanie różniczkowe metodą odwrotnego przekształcenia Laplace’a:
a.
3
)
0
(
,
2
)
0
(
)
(
1
8
)
(
4
)
(
)
(
3
'
2
2
−
=
=
⋅
=
−
+
+
+
y
y
t
t
y
dt
t
dy
dt
t
y
d
b.
5
)
0
(
,
0
)
0
(
)
(
1
8
)
(
4
)
(
4
)
(
'
2
2
=
=
⋅
=
+
+
+
+
y
y
t
t
y
dt
t
dy
dt
t
y
d
30
Automatyka i sterowanie – przekształcenie Laplace’a, przykłady
c.
0
)
0
(
,
2
)
0
(
)
(
1
34
)
(
34
)
(
6
)
(
'
2
2
=
−
=
⋅
=
+
+
+
+
y
y
t
t
y
dt
t
dy
dt
t
y
d
Document Outline
Wyszukiwarka
Podobne podstrony:
ais 03 id 53431 Nieznany (2)
ais 01 id 53429 Nieznany (2)
ais 04 id 53433 Nieznany (2)
ais d05 id 53449 Nieznany (2)
ais d01 id 53441 Nieznany (2)
ais d03 id 53445 Nieznany (2)
ais 07 id 53437 Nieznany (2)
ais 05 id 53435 Nieznany (2)
ais d04 id 53447 Nieznany (2)
ais d02 id 53443 Nieznany (2)
ais 03 id 53431 Nieznany (2)
AIS id 53428 Nieznany
AiR ais cw 6 MRJ3A id 53377 Nieznany (2)
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
więcej podobnych podstron