Transformata “z” i filtry - © Przemysław Korohoda, KE, AGH
Instrukcja do laboratorium z cyfrowego przetwarzania sygnałów
Transformata Z; blokowe struktury opisujące filtr
© Przemysław Korohoda, KE, AGH
Zawartość instrukcji:
1 Materiał z zakresu DSP
1.1 Transformata “Z”
1.2 Transmitancja “Z”
1.3 Blokowa struktura filtru
1.4 Zmienne stanu
2 Korzystanie z pakietu MATLAB
2.1 Struktury filtrów używane w Matlab’ie
2.2 Opis wybranych funkcji pakietu
Do sprawnego wykonania ćwiczenia nie jest konieczna wcześniejsza praktyczna znajomość nie wprowadzonych w
ramach poprzednich ćwiczeń funkcji pakietu MATLAB, jednak niezbędna jest dobra orientacja w materiale
przedstawionym w częściach 1 oraz 2 tej instrukcji oraz w zagadnieniach będących przedmiotem poprzednich ćwiczeń.
Dlatego też wskazane jest dokładne przeczytanie obu wymienionych części instrukcji oraz zanalizowanie podanych
przykładów. UWAGA: znajomość i zrozumienie części 1 i 2 oraz materiału z poprzednich ćwiczeń mogą zostać przez
prowadzącego skontrolowane w trakcie zajęć.
1
Transformata “z” i filtry - © Przemysław Korohoda, KE, AGH
1 Materiał z zakresu DSP
UWAGA: Rozważane są wyłącznie systemy liniowe, niezmienne względem przesunięcia.
1.1 Transformata “Z”
Ważnym narzędziem w badaniu i projektowaniu systemów (filtrów) cyfrowych jest transformacja “Z”. Istnieją dwie
podstawowe odmiany tej transformacji - jednostronna i dwustronna. Obie polegają na wyznaczeniu dla zadanego ciągu,
oznaczonego przykładowo jako
x n
[ ]
, transformaty będącej funkcją ciągłej zmiennej zespolonej, oznaczanej zwykle
jako “z”. Nie ma znaczenia, czy
x n
[ ]
reprezentuje sygnał, czy na przykład odpowiedź impulsową. Będzie on niekiedy
nazywany ciągiem pierwotnym lub oryginalnym. Analogicznie dziedzina indeksów “n” będzie nazywana dziedziną
pierwotną lub oryginalną, natomiast dziedzina “z” - dziedziną transformaty “Z” (lub w skrócie, gdy nie będzie to
powodowało nieporozumień - dziedziną transformaty).
Jednostronna transformata “Z” ciągu x[n] dana jest wzorem.
(1)
X z
x n z
n
n
( )
[ ]
=
⋅
=
∞
−
∑
0
natomiast dwustronna transformata “Z”:
(1a)
X z
x n z
n
n
( )
[ ]
=
⋅
=−∞
∞
−
∑
Znacznie częściej stosuje się transformację dwustronną (1a) i na tej wersji będą bazowały dalsze rozważania.
Dla wielu typowych ciągów
x n
[ ]
wzór (1a) nie jest zbieżny (do wartości o skończonym module) dla dowolnej
zespolonej liczby “z”. Przykładowo łatwo jest sprawdzić, że dla
x n
u n
[ ]
[
]
= −
oraz
z
= 1
wzór (1a) nie jest zbieżny.
Wartości “z”, dla których transformata jest zbieżna tworzą na płaszczyźnie zespolonej pewien obszar zwany obszarem
zbieżności. Dyskusja obszarów zbieżności nie będzie przedmiotem ćwiczeń, jednak warto o tym ograniczeniu pamiętać
i w prostych przypadkach umieć określić obszar zbieżności. Dokładniejsze wyjaśnienia można znaleźć w podanej
literturze uzupełniającej.
Transformata (o ile istnieje) zawiera pełną informację umożliwiającą idealne odtworzenie ciągu pierwotnego za
pomocą transformacji odwrotnej. Zwykle informacja ta jest zawarta w transformacie z dość dużą nadmiarowością. Do
wyznaczenia transformaty odwrotnej wystarczy bowiem znać postać transformaty “Z” wzdłuż dowolnej krzywej
zamkniętej, obejmującej na płaszczyźnie “z” punkt (0,0) - może to być na przykład okrąg. Oczywiście krzywa ta musi
zawierać się w obszarze zbieżności, bo poza nim transformata nie istnieje. Wyznaczanie transformaty odwrotnej
według odpowiedniego wzoru definicyjnego nie będzie tematem ćwiczeń, zatem dalszych wyjaśnień należy szukać w
literaturze uzupełniającej.
Transformacja “Z” jest liniowa, czyli dla dowolnych liczb i
b
oraz ciągów posiadających transformaty “Z”
zachodzi:
a
(2)
x n
X z
y n
Y z
a x n
b y n
a X z
b Y z
Z
Z
Z
[ ]
( )
[ ]
( )
[ ]
[ ]
( )
( )
← →
⎯
∧
← →
⎯
⇓
⋅
+ ⋅
← →
⎯
⋅
+ ⋅
W ramach przygotowania do ćwiczeń laboratoryjnych należy przećwiczyć wykazanie tej cechy za pomocą wzoru (1a) i
odpowiednich przekształceń.
Jedną z ważniejszych właściwości transformacji “Z” jest fakt, że przesunięciu ciągu w dziedzinie pierwotnej
odpowiada pomnożenie transformaty tego ciągu przez wartość “z” w odpowiedniej potędze:
(
) (
)
x n
X z
x n k
z
X z
Z
Z
k
[ ]
( )
[
]
( )
← →
⎯
⇔
− ← →
⎯
⋅
−
(3)
Można to wykazać za pomocą wzoru definicyjnego (1a) i podstawienia
l
n k dla
k
= −
< ∞
:
(4)
x n k z
x l z
z
x l z
n
l k
l
k
l
n
[
]
[ ]
[ ]
− ⋅
=
⋅
=
⋅
−
− −
=−∞
∞
−
=−∞
∞
=−∞
∞
∑
∑
∑
l
−
Jaka jest transformata „z” delty Kroneckera oraz delty Kroneckera przesuniętej w czasie? Jakie są odpowiednie obszary
zbieżności?
2
Transformata “z” i filtry - © Przemysław Korohoda, KE, AGH
Z (4) oraz liniowości transformacji “Z” wynika, że liniowa kombinacja kopii ciągu
x n
[ ]
poprzesuwanych w
dziedzinie indeksów posiada następującą transformatę:
(5)
(
)
x n
X z
a x n
a x n
a
x n k
a X z
a z
X z
a z
X z
Z
k
Z
k
k
[ ]
( )
[ ]
[
]
[
]
( )
( )
( )
← →
⎯
⋅
+
⋅
− +
+
⋅
− +
← →
⎯
⋅
+
⋅
⋅
+
+
⋅
⋅
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟
−
− +
c
L
L
1
2
1
2
1
1
1
1
Z (5) wynika transformata “Z” równania różnicowego:
(6)
a
y n k
b
x n m
Z
a z
Y z
b z
X z
k
k
K
m
m
M
k
k
k
K
m
m
m
M
⋅
− +
=
⋅
− +
⋅
⋅
=
⋅
⋅
=
=
− +
=
− +
=
∑
∑
∑
∑
[
]
[
( )
( )
1
1
1
1
1
1
1
1
b
]
1.2 Transmitancja “Z”
Za pomocą elementarnych przekształceń można transformatę (6) sprowadzić do następującej postaci (zakładamy, że
wcześniej zadbano by
a
):
1
1
=
Y z
X z
H z
b
b z
b z
b
z
a z
a z
a
z
M
M
K
K
( )
( )
( )
=
=
+
⋅
+ ⋅
+
+
⋅
+
⋅
+
⋅
+
+
⋅
−
−
−
−
−
−
1
2
1
3
2
1
2
1
3
2
1
L
L
+
+1
(7)
Otrzymaną funkcję ciągłej zmiennej zespolonej “z”, czyli
H z
( )
, nazywa się transmitancją systemu. Ponieważ
transmitancja zawiera identyczne współczynniki, co odpowiadające jej równanie różnicowe, więc zawiera dokładnie tę
samą informację o systemie, zatem dyskusja cech systemu w zależności od warunków początkowych dotyczy jej w tym
samym stopniu.
Dla równania różnicowego w postaci nierekursywnej - odpowiadającego systemowi FIR - postać transmitancji (7) jest
nieco prostsza:
Y z
X z
H z
b
b z
b z
b
z
M
M
( )
( )
( )
=
=
+
⋅
+ ⋅
+
+
⋅
−
−
−
1
2
1
3
2
L
+1
(8)
Wynika stąd, że ponieważ odpowiedź impulsowa składa się z elementów będących współczynnikami prawej strony
równania różnicowego (
h k
b
k
[ ]
=
), więc w tym przypadku transmitancja jest transformatą odpowiedzi impulsowej:
(9)
h n
H z
Z
[ ]
( )
← →
⎯
Dla systemów typu IIR zależność (9) jest także aktualna. Pomijając problematykę zbieżności transformaty, można to
wykazać w sposób następujący. Mimo, że w praktyce jest to mało przydatne, to dla potrzeb teoretycznych rozważań
odpowiedź impulsową filtru typu IIR można zapisać za pomocą sumy o nieskończonej ilości składników:
(10)
h n
h k d n k
k
[ ]
[ ] [
]
=
⋅
=−∞
∞
∑
−
Transformata “Z” takiej odpowiedzi impulsowej jest zatem przedstawiona poniżej:
(11)
h n
H z
h k z
Z
k
k
[ ]
( )
[ ]
← →
⎯
′
=
⋅
−
=−∞
∞
∑
Współczynniki
nie uległy zmianie, gdyż z punktu widzenia transformacji są to stałe - nie zależą od
n
. Splot
liniowy sygnału i odpowiedzi impulsowej (skończonej lub nieskończonej) określa odpowiedź systemu na ten sygnał.
h k
[ ]
Porównując zatem związek pomiędzy ciągiem
x n
[ ]
i
y n
[ ]
opisany za pomocą
oraz związek pomiędzy
odpowiednimi transformatami zapisany dla systemów FIR w (8) można stwierdzić, że splot liniowy w dziedzinie
pierwotnej (indeksów) odpowiada mnożeniu odpowiednich transformat:
h n
[ ]
3
Transformata “z” i filtry - © Przemysław Korohoda, KE, AGH
(12)
y n
x n h n
Y z
X z H z
Z
[ ]
[ ] [ ]
( )
( )
( )
=
∗
← →
⎯
=
⋅
Zależność (12) jest prawdziwa także dla systemów IIR. Aby to wykazać można posłużyć się ogólniejszym
wyprowadzeniem niż przedstawione powyżej dla systemów FIR. Jeżeli system liniowy, stacjonarny jest opisany za
pomocą odpowiedzi impulsowej (która może być nieskończona), to jego odpowiedź na sygnał
x n
[ ]
można wyznaczyć
za pomocą splotu liniowego i splot ten można również poddać transformacji “Z” (należy pamiętać, że w tym przypadku
wartości ciągów zależne wyłącznie od indeksu “k” są traktowane jako stałe):
(13)
y n
h k x n k
Y z
h k z
X z
k
Z
k
k
[ ]
[ ] [
]
( )
[ ]
( )
=
⋅
−
← →
⎯
=
⋅
⋅
=−∞
∞
−
=−∞
∞
∑
∑
Po zamianie w otrzymanej transformacie liter indeksów sumowania z “k” na “n” (co nie było konieczne, jednak zostało
przeprowadzone dla podkreślenia związku ze wzorem (1a)) oraz wyciągnięciu wspólnego elementu przed znak sumy
otrzymuje się równość potwierdzającą prawdziwość wzoru (12):
(14)
Y z
X z
h n z
X z H z
n
n
( )
( )
[ ]
( )
( )
=
⋅
⋅
⎛
⎝
⎜
⎞
⎠
⎟ =
⋅ ′
−
=−∞
∞
∑
Otrzymany wynik potwierdza także, że transmitancja
H z
( )
określona równaniem (7) jest transformata równa
odpowiedzi impulsowej
według równania (11).
′
H z
( )
Transmitancja (7) posiada w liczniku i mianowniku ujemne potęgi zmiennej ”z”. W celu zapisu transmitancji z
wykorzystaniem wyłącznie dodatnich potęg tej zmiennej należy w zależności (7) pomnożyć licznik i mianownik przez
odpowiednią potęgę “z”, wymaga to jednak rozróżnienia trzech przypadków:
a) dla
K
M
>
H z
b z
b z
b z
b
z
z
a z
a z
a
K
K
K
M
K M
K
K
K
K
( )
=
⋅
+
⋅
+ ⋅
+
+
⋅
+
⋅
+
⋅
+
+
−
−
−
−
−
−
1
1
2
2
3
3
1
2
2
3
3
L
L
−
(15a)
b) dla
K
M
<
H z
b z
b z
b z
b
z
a z
a z
a
z
M
M
M
M
M
M
M
K
M N
( )
=
⋅
+
⋅
+ ⋅
+
+
+
⋅
+
⋅
+
+
⋅
−
−
−
−
−
−
1
1
2
2
3
3
1
2
2
3
3
L
L
−
(15b)
c) dla
K
M
=
H z
b z
b z
b z
b
z
a z
a z
a
K
K
K
M
K
K
K
K
( )
=
⋅
+
⋅
+ ⋅
+
+
+
⋅
+
⋅
+
+
−
−
−
−
−
−
1
1
2
2
3
3
1
2
2
3
3
L
L
(15c)
Postać wzorów (15) jest oparta na współczynnikach wielomianów licznika i mianownika. Tę samą transmitancję można
opisać za pomocą miejsc zerowych licznika i mianownika, czyli zer (z) i biegunów (p):
(
) (
) (
)
(
) (
) (
)
H z
K
z z
z z
z z
z p
z p
z p
m
M
K
( )
=
⋅
−
⋅ −
⋅ ⋅ −
−
⋅ −
⋅ ⋅ −
−
−
1
2
1
2
L
L
1
1
(16)
Jak łatwo zauważyć:
K
b
a
b
m
=
=
1
1
1
.
Pamiętając o związku transmitacji z równaniem różnicowym, łatwo teraz pokazać, w jaki sposób można tworzyć
równoważne równania różnicowe (a w szczególności, jak system nierekursywny opisać za pomocą struktury
rekursywnej). Wystarczy w transmitancji w postaci (16) pomnożyć licznik i mianownik przez te same czynniki
wprowadzające dodatkowe miejsca zerowe do licznika i mianownika. Z punktu widzenia funkcjonowania systemu
wprowadzone dodatkowe zera i bieguny redukują się wzajemnie, jednak po przekształceniu do postaci równania
różnicowego można stwierdzić pojawienie się nowych czynników po obu stronach równania. Z opisanych powiązań
można także skorzystać, chcąc sprawdzić, czy określone rekursywne równanie różnicowe opisuje system FIR - jeżeli
tak, to bieguny położone poza punktem (0,0) powinny redukować się z odpowiednimi zerami transmitancji.
Należy jednak pamiętać, że zera i bieguny mogą być liczbami zespolonymi, co nie zawsze prowadzi do równania
różnicowego o współczynnikach pozbawionych części urojonej. W ramach ćwiczeń trzeba będzie sprawdzić, jakie
4
Transformata “z” i filtry - © Przemysław Korohoda, KE, AGH
warunki powinny spełniać zera i bieguny, by danej transmitancji odpowiadało równanie różnicowe o wyłącznie
rzeczywistych współczynnikach.
Różne formy opisu tego samego systemu - równanie różnicowe, odpowiedź impulsowa, transmitancja - mogą się
okazać przydatne dlatego, iż w każdej z nich w łatwy sposób można określić pewne wybrane cechy systemu. Jak
pokazano powyżej transmitancja w postaci zer i biegunów ukazuje wprost, czy system może mieć strukturę
nierekursywną. Inną cechą łatwą do sprawdzenia jest stabilność (w sensie BIBO). Aby filtr przyczynowy był stabilny
potrzeba i wystarcza, by wszystkie bieguny (czyli miejsca zerowe mianownika) znajdowały się wewnątrz okręgu
jednostkowego o środku w środku układu współrzędnych. Warto się zastanowić z czego ta właściwość wynika (patrz
też literatura uzupełniająca). Powyższy warunek stabilności jest oczywiście spełniony dla wszystkich systemów typu
FIR.
1.3 Blokowa struktura filtru
Dany filtr można opisać za pomocą schematu blokowego na wiele sposobów. Jednak z punktu widzenia realizacji
nawiązujących do równania różnicowego lub transmitancji ”Z” istotne znaczenie mają dwie podstawowe struktury
opisane poniżej. Schematy składają się z elementów trzech typów: sumatora, elementu mnożącego oraz elementu
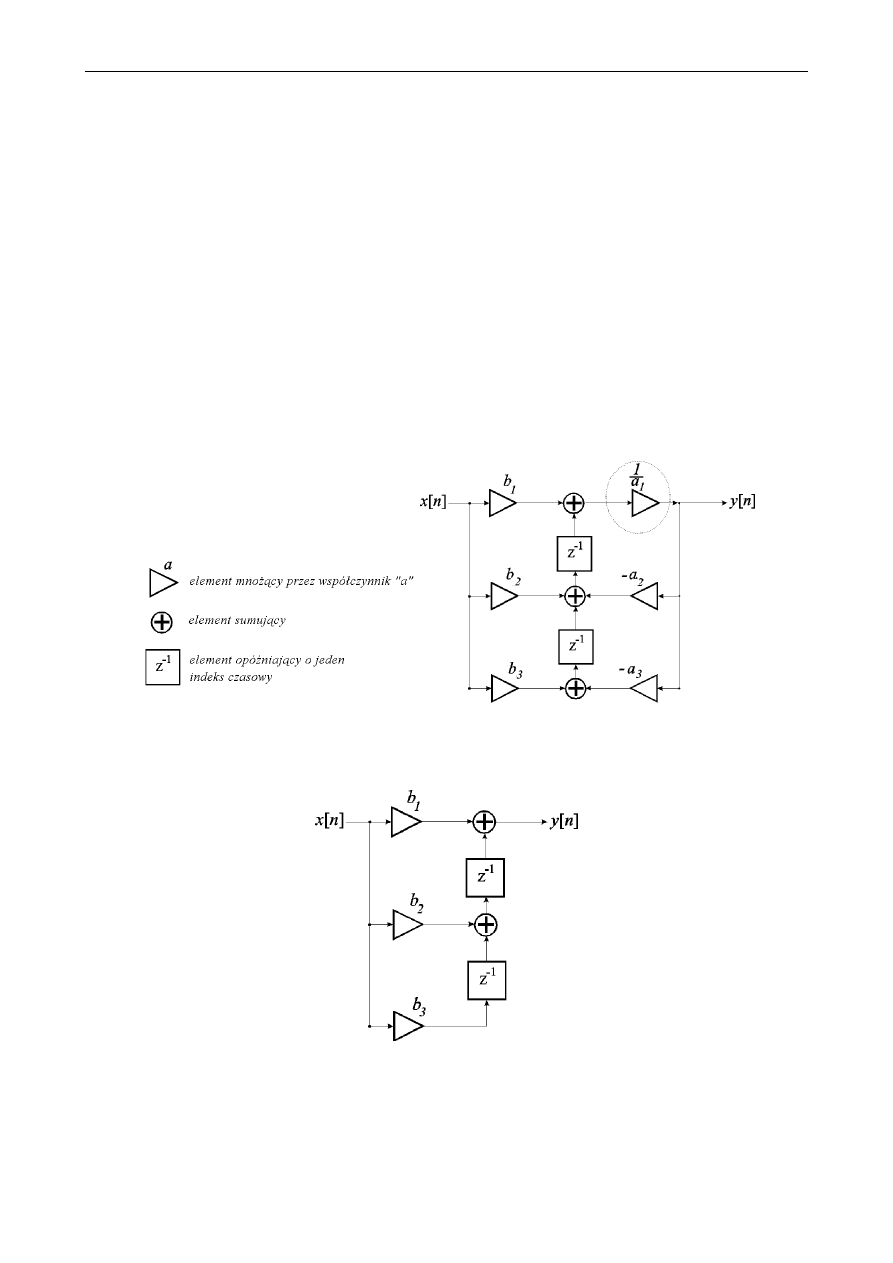
opóźniającego. Ponadto schematy te pokazują kierunki przepływu sygnałów. Rys.1 przedstawia przykład typowej
struktury blokowej filtru drugiego rzędu, powstałą bezpośrednio z poniższego równania różnicowego:
a y n
b x n
b x n
b x n
a y n
a y n
1
1
2
3
2
3
1
2
1
⋅
= ⋅
+
⋅
2
− + ⋅
− −
⋅
− −
⋅
−
[ ]
[ ]
[
]
[
]
[
]
[
]
(17)
Rys. 1. Przykładowa struktura filtru typu I, równoważna transponowanej strukturze typu II
(ang. Direct form II transposed)
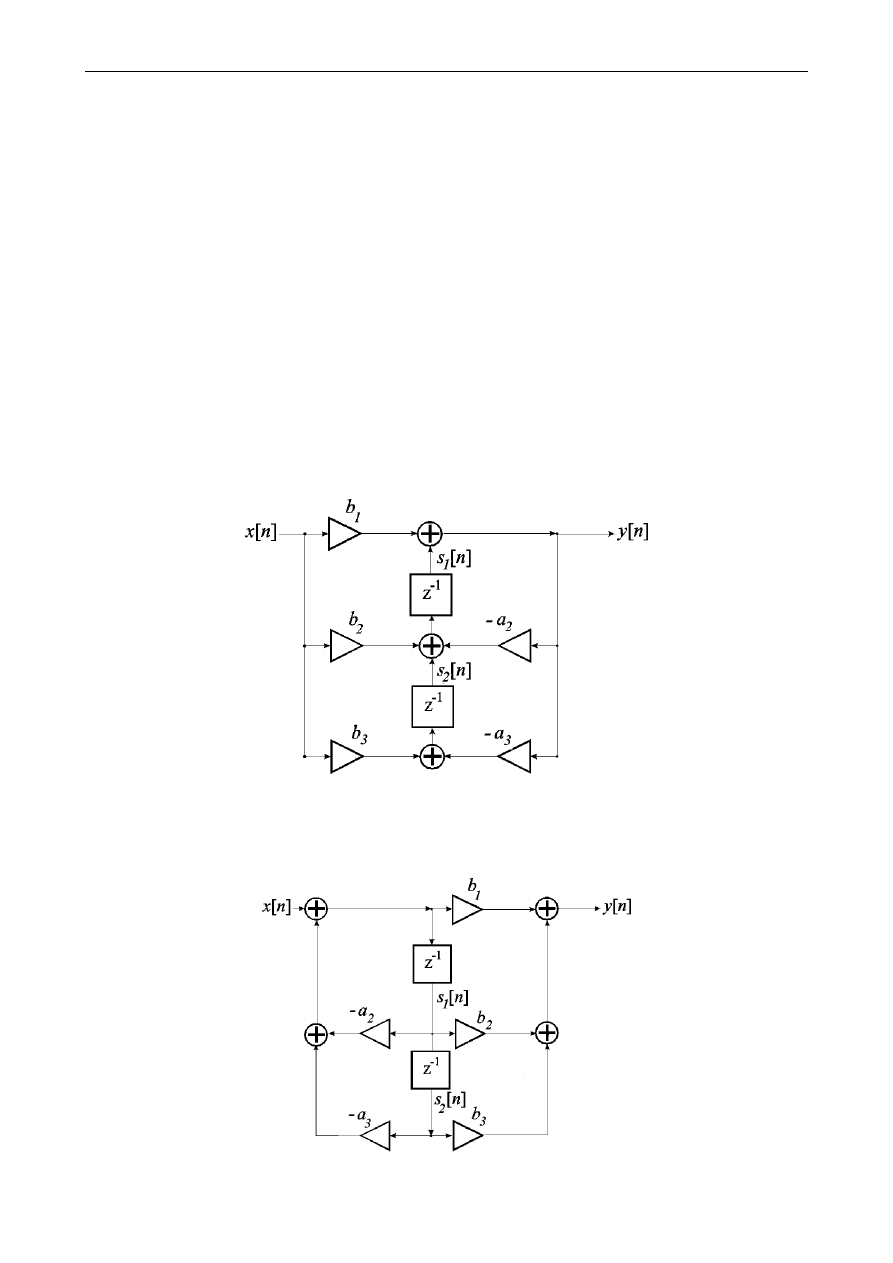
Na rys.2 pokazano przykład nierekursywnej struktury filtru drugiego rzędu.
Rys. 2. Struktura filtru drugiego rzędu realizująca splot liniowy ciągu wejściowego
x n
[ ]
oraz ciągu współczynników “b”, ciąg
y n
[ ]
jest wynikiem splatania
5
Transformata “z” i filtry - © Przemysław Korohoda, KE, AGH
1.4 Zmienne stanu
Ten sam system, opisany za pomocą transmitancji – w postaci (16) – albo równania różnicowego, może być także
opisany za pomocą czterech macierzy A, B, C, D, o odpowiednich wymiarach, z wykorzystaniem zmiennych stanu,
które stanowią wektor ciągów oznaczony poniżej jako
:
s n
[ ]
s n
A s n
B x n
y n
C s n
D x n
[
]
[ ]
[ ]
[ ]
[ ]
[ ]
+ = ⋅
+ ⋅
= ⋅
+ ⋅
1
(18)
Opis (18) jest równoważny opisowi za pomocą równania różnicowego (otrzymanego przez wyrugowanie z (18)
zmiennych stanu) lub też transmitancji:
(
)
H z
C z I
A
B D
( )
= ⋅ ⋅ −
⋅ +
−1
(19)
gdzie I to macierz jednostkowa - tj. posiadająca „1” na diagonalnej i „0” w pozostałych miejscach.
W przypadku przykładu z rys.3 wektor zmiennych stanu z równania (19) jest dwuelementowy (składa się z dwóch
ciągów):
(20)
s n
s n
s n
[ ]
[ ]
[ ]
=
⎡
⎣
⎢
⎤
⎦
⎥
1
2
Dla przedstawionego przykładu macierze opisujące filtr za pomocą zmiennych stanu według równania (19) mają
następujące wymiary:
,
,
,
.
A
x
2 2
B
x
2 1
C
x
1 2
D
x
1 1
Rys.3. Filtr w postaci struktury typu Transposed direct form II z zaznaczonymi zmiennymi stanu
Transpozycja struktury filtru polega na zamianie kolumn ze współczynnikami „a” i „b”, odwróceniu kierunków
przepływu w gałęziach poziomych i pionowych oraz przeniesieniu elementów sumujących z gałęzi centralnych na
brzegowe (lub odwrotnie).
Rys.4. Filtr w postaci struktury typu Direct form II z zaznaczonymi zmiennymi stanu
6
Transformata “z” i filtry - © Przemysław Korohoda, KE, AGH
Rząd filtru jest równy ilości elementów opóźniających w jego strukturze - czyli ilości zmiennych stanu.
Przedstawiony opis filtru za pomocą zmiennych stanu ma sens tylko wtedy, gdy filtr jest liniowy i niewrażliwy na
przesunięcie.
Jako ćwiczenie przygotowujące należy porównać opis w postaci zmiennych stanu dla obu przedstawionych typów
struktur (macierze A,B,C,D), gdy wiadomo, że dany system przyczynowy jest opisany równaniem:
a)
y n
y n
x n
[ ]
[
]
[ ]
−
− = ⋅
1
2
b)
y n
y n
x n
x n
[ ]
,
[
]
[ ]
,
[
]
−
⋅
− = ⋅
−
⋅
−
0 5
1
2
0 5
1
7
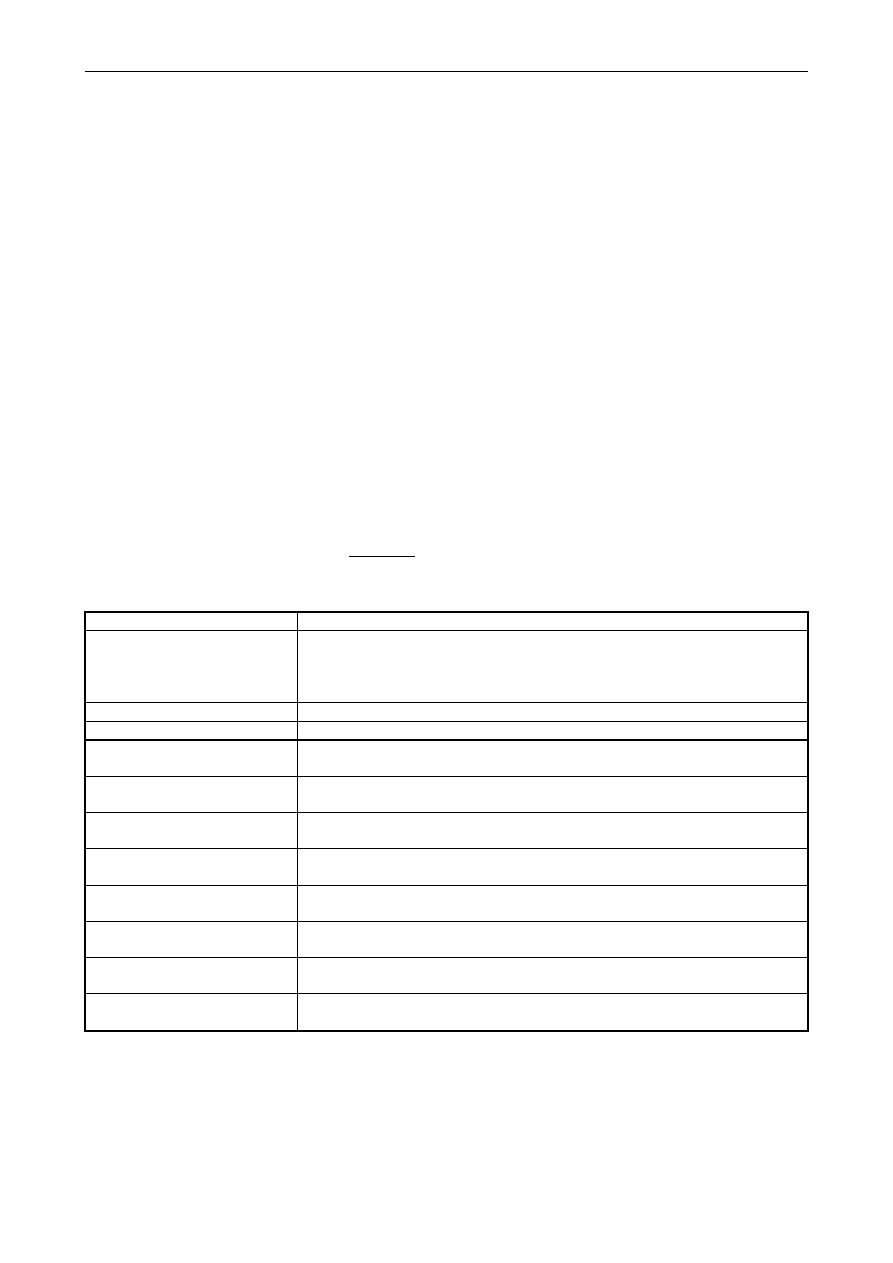
Transformata “z” i filtry - © Przemysław Korohoda, KE, AGH
2 Korzystanie z pakietu MATLAB
2.1 Struktury filtrów używane w Matlab’ie
Postać ogólna instrukcji filter (z warunkami początkowymi):
[wyjscie,warunki_koncowe]=filter(b,a,x,zin); gdzie b, a, x, zin oznaczają kolejno: wektory współczynników “b”,
“a”, ciąg wejściowy oraz warunki początkowe
Element wzmacniający struktury z rys.1 otoczony przerywaną linią nie jest zazwyczaj uwzględniany Współczynnik
przyjmuje się wtedy jako równy “1”, skalując odpowiednio pozostałe współczynniki. W takim przypadku można
ten element pominąć na schemacie. Jednak instrukcja filter wymaga zawsze podania niezerowej wartości
, która w
razie potrzeby może być różna od “1”, o czym należy pamiętać podając wektor współczynników „a”.
a
1
a
1
Odpowiedź filtru składa się z odpowiedzi wymuszonej (w wyniku podania niezerowego sygnału na wejście) oraz z
odpowiedzi swobodnej (na niezerowe warunki początkowe). Obie odpowiedzi sumują się dając sygnał wyjściowy
filtru. Warunki początkowe opisane są za pomocą zmiennych stanu - w przypadku Matlab’a są to sygnały wyjściowe z
elementów opóźniających - patrz rys.1 (wiele podręczników definiuje jako zmienne stanu sygnały wejściowe
elementów opóźniających, naturalnie obie wersje są z punktu widzenia zastosowań równoważne, wymagają jedynie
modyfikacji indeksów czasowych przy dalszym wykorzystywaniu zmiennych stanu). Warto się zastanowić - ogólnie
lub na przykładzie systemów z ćwiczenia na końcu poprzedniego rozdziału - jak taka zmiana w definicji zmiennych
stanu może wpłynąć na postać równania (19) oraz zawartość macierzy A,B,C,D.
UWAGA 1: Przy wyznaczaniu za pomocą funkcji filter odpowiedzi swobodnej filtru na niezerowe warunki
początkowe wartość współczynnika
jest zawsze przyjmowana jako równa “1”, natomiast odpowiedź
wymuszona wyliczana jest przy uwzględnieniu podanej przez użytkownika wartości tego współczynnika.
a
1
UWAGA 2: Przy korzystaniu z funkcji zamiany postaci opisu filtru tf2ss oraz tf2zp należy dopilnować, by wektory
współczynników licznika i mianownika były tej samej długości (w razie potrzeby należy je dopełnić zerami).
UWAGA 3: Strukturę typu Direct form II założono w funkcjach: tf2ss, ss2tf, zp2ss, ss2zp.
Strukturę typu Direct form II transposed założono w funkcjach filter oraz filtic.
2.2 Opis wybranych funkcji pakietu
Funkcja Opis
filtic
przeliczenie podanych ciągów wejściowego i wyjściowego dla indeksów
czasowych poprzedzających początek aktualnej filtracji na zmienne stanu filtru o
podanych współczynnikach - czyli wyznaczenie warunków początkowych dla
instrukcji filter w oparciu o ciągi: wejściowy i wyjściowy z „przeszłości”
poly wyznaczanie
współczynników wielomianu o podanych miejscach zerowych
roots
wyznaczanie miejsc zerowych wielomianu o podanych współczynnikach
ss2zp
przeliczenie opisu filtru z macierzy dla zmiennych stanu na zera i bieguny
transmitancji
ss2tf
przeliczenie opisu filtru z macierzy dla zmiennych stanu na współczynniki licznika
i mianownika transmitancji
zp2ss
przeliczenie opisu filtru z postaci zer i biegunów transmitancji na odpowiednie
macierze opisu za pomocą zmiennych stanu
zp2tf
przeliczenie opisu filtru z postaci zer i biegunów transmitancji na współczynniki
licznika i mianownika transmitancji
tf2zp
przeliczenie opisu filtru z postaci współczynników licznika i mianownika
transmitancji na zera i bieguny transmitancji
tf2ss
przeliczenie opisu filtru z postaci współczynników licznika i mianownika
transmitancji na odpowiednie macierze opisu za pomocą zmiennych stanu
impz
wyznaczanie odpowiedzi impulsowej filtru o zadanej transmitancji „z”
(transmitancję można określić za pomocą współczynników licznika i mianownika)
zplane zaznaczanie
na
płaszczyźnie zespolonej zer i biegunów transmitacji podanej w
postaci współczynników licznika i mianownika lub w postaci zer i biegunów
Szczegółowy opis powyższych funkcji dostępny jest po wywołaniu funkcji help z nazwą funkcji jako parametrem, np:
>>help ss2zp;
Jeżeli wektory opisujące transmitancję dla funkcji zplane są wektorami wierszowymi, wówczas są traktowane jako
zera i bieguny opisujące transmitancję. Funkcja zplane umożliwia także wykreślenie zer i biegunów wprost z
wielomianowej postaci transmitancji. Kolejne współczynniki wielomianów licznika i mianownika (w takiej właśnie
kolejności) należy w takiej sytuacji podać w postaci wektorów kolumnowych.
8