Ć w i c z e n i e 40

WYZNACZANIE MODUŁU SPRĘŻYSTOŚCI PRZY PO-

MOCY WAHADŁA TORSYJNEGO

40.1 Opis teoretyczny

Jeśli jeden z końców długiego jednorodnego pręta sztywno zamocować, a do drugiego przyłożyć
skręcający moment sił M, to koniec ten przekręci się o kąt

φ, przy czym zgodnie z prawem Hooke’a

Φ

= D

M

(40.1)

Stała (dla danego pręta) wielkość D nosi nazwę modułu skręcenia (lub momentu kierującego). Li-
niowa zależność pomiędzy M i

φ wyrażona wzorem (40.1) zachodzi tylko dla niewielkich wartości

M. W ogólnym przypadku zależność

φ = φ(M) może być nieliniowa, lub nawet niejednoznaczna.

Wielkość D nie charakteryzuje jednoznacznie właściwości materiału podczas skręcenia, dlatego
wprowadza się wielkość nazwaną modułem sprężystości G.
Wprowadzony teraz zależnością wiążącą moduł sprężystości G oraz moduł skręcenia D. Po odchy-
leniu ciała o kąt

α od położenia równowagi wytwarza się nowy stan równowagi, w którym reakcja

pręta (moment M) równoważy moment siły zewnętrznej M

Z

. Po uwolnieniu ciała powstają drgania

pod wpływem momentu siły

M

Z

= – D

α

zwracającego ciało zawsze do położenia równowagi. Równanie ruchu ma więc postać analogiczną,
jak dla wahadła grawitacyjnego

α

α

D

J

2

2

−

=

dt

d

A zatem i okres drgań wyraża się tym samym wzorem

D

J

π

2

T

=

(40.2)

gdzie J jest momentem bezwładności drgającej bryły względem zadanej osi obrotu.
Wielkość modułu skręcenia D musimy określić w zależności od warunków fizycznych narzuconych
w ćwiczeniu.
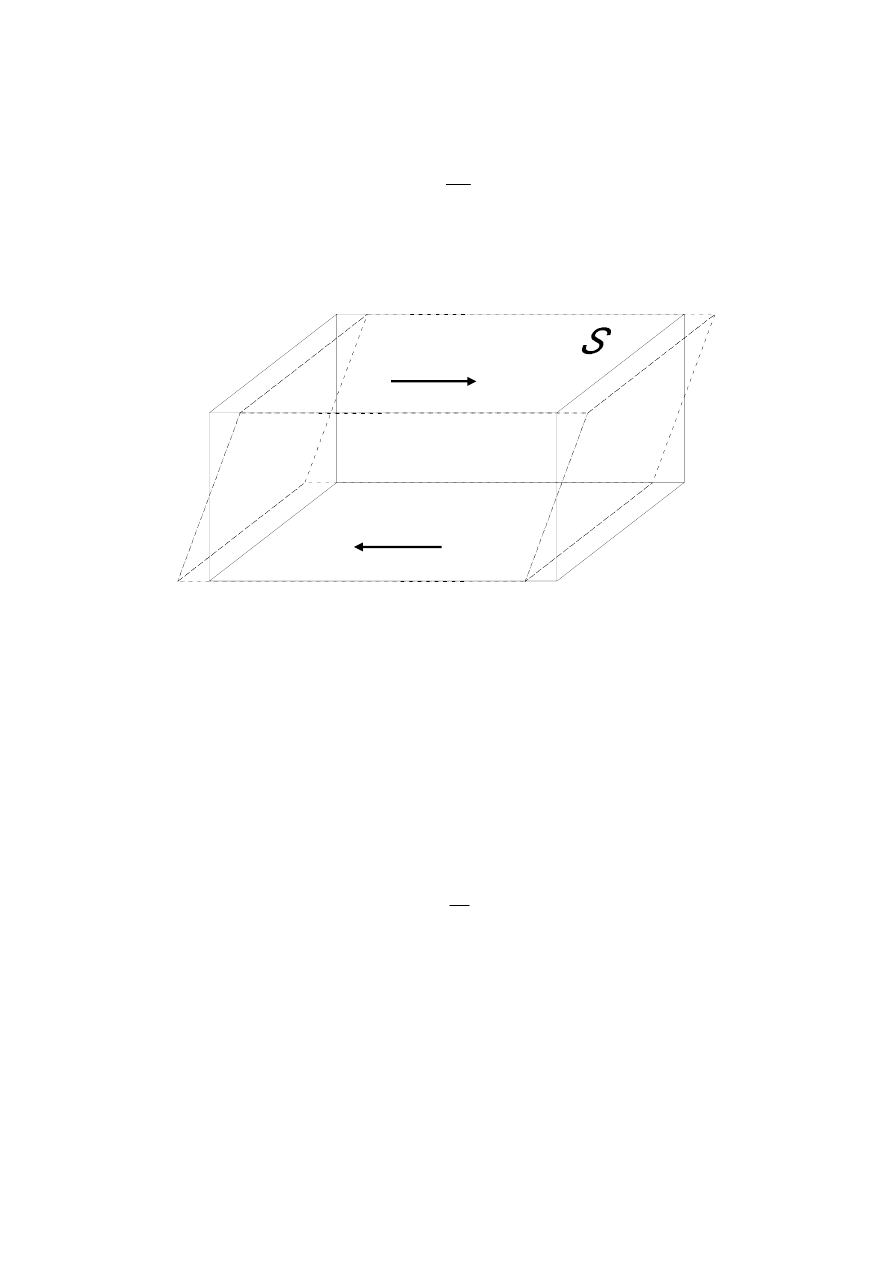
Rozważymy teraz przypadek, gdy siły działające na ciało powodują jego odkształcenie sprężyste
(deformacja zanika po ustąpieniu siły odkształcającej F). W zależności od kąta utworzonego przez
wektory siły działającej z powierzchnią ciała odkształconego rozróżniamy siły normalne tj. działa-
jące prostopadle do powierzchni, oznaczać je będziemy symbolem F

n

, oraz siły styczne – działające

stycznie do powierzchni – F

S.

Naprężeniem normalnym

σ nazywamy stosunek siły normalnej do pola powierzchni, na którą ta siła

działa:

S

F

n

=

σ

Miarą odkształcenia, jakiego ciało doznaje pod wpływem takiej siły, jest wielkość

Z

∆Z

ε

=

Odkształcenie względne, będące stosunkiem zmiany długości ciała

∆Z w kierunku zgodnym z kie-

runkiem działania siły do długości początkowej Z (rzs.40.1.a).

Rys.40.1. Działanie na ciało sił normalnych F

n

(a) i sił stycznych F

S

(b) do powierzchni.

Między wielkościami

σ i ε zachodzi związek znany jako prawo Hooke a

σ = Eε

Współczynnik proporcjonalności E zwany modułem Younga jest równy liczbowo naprężeniu, które
powoduje odkształcenie względem danego ciała równe jedności (dwukrotne wydłużenie).

Naprężenie styczne

τ jest to stosunek siły stycznej F

S

do powierzchni S, na którą ta siła działa.

Efekt działania takiego naprężenia nazywamy ścinaniem prostym

S

F

S

=

τ

Odkształcenie względne mierzy się wtedy za pomocą tzw. kąta ścinania

γ tj. kąta jaki tworzy płasz-

czyzna pierwotna z płaszczyzną odwróconą na skutek ścinania (rys.40.1.b). Prawo Hooke’a przyj-
muje postać:

τ = Gγ

Współczynnik G zwany modułem sprężystości ma wymiar Nm

-2

rad

-1

.

Podczas odkształcenia sprężystego następującego pod wpływem działania sił normalnych zachodzi
zmiana wszystkich wymiarów ciała. Względne zwężenie jest proporcjonalne do względnego wy-
dłużenia ciała

γ

-F

s

F

s

Z

∆Z

Y

∆Y

ν

=

Wielkość

ν nazywamy współczynnikiem Poissona, zaś między trzema wprowadzonymi tu współ-

czynnikami zachodzi związek

)

1

(

2

E

G

ν

+

=

W naszym ćwiczeniu wielkość G wyznaczamy wykorzystując drgania harmoniczne pręta metalo-
wego, zachodzące pod wpływem sił sprężystości.
Każdy z elementów badanego drutu, skręconego przez siłę zewnętrzną, podlega deformacji ścinania
prostego. Jako reakcja na tę siłę pojawia się w pręcie siła sprężystości powodująca powrót do poło-
żenia równowagi i w konsekwencji wywołująca zjawisko drgań. Wprowadzimy zależność matema-
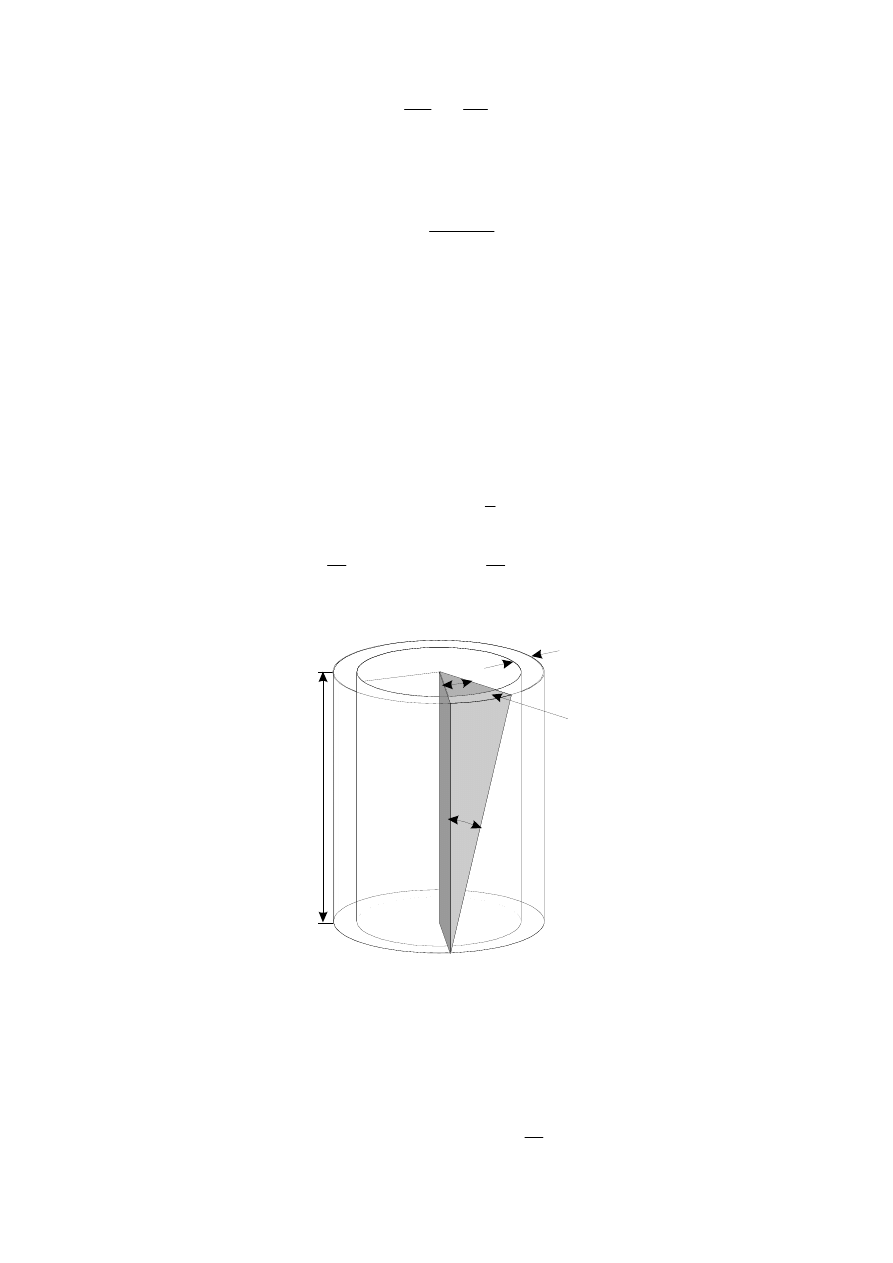
tyczną między modułem sprężystości G, a momentem sił działającym na skręcony pręt. Rozważa-
my cylindryczny element pręta o promieniu wewnętrznym r

*

, grubości dr

*

i długości całego pręta

l

>> r

*

(rys.40.2). Dla pierścienia pokazanego na rysunku mamy:

l

s

G

G

=

=

γ

τ

gdzie s jest elementem łuku, ale

α

=

*

r

s

a więc

α

τ

l

r

*

G

=

Rys.40.2. Skręcenie pręta

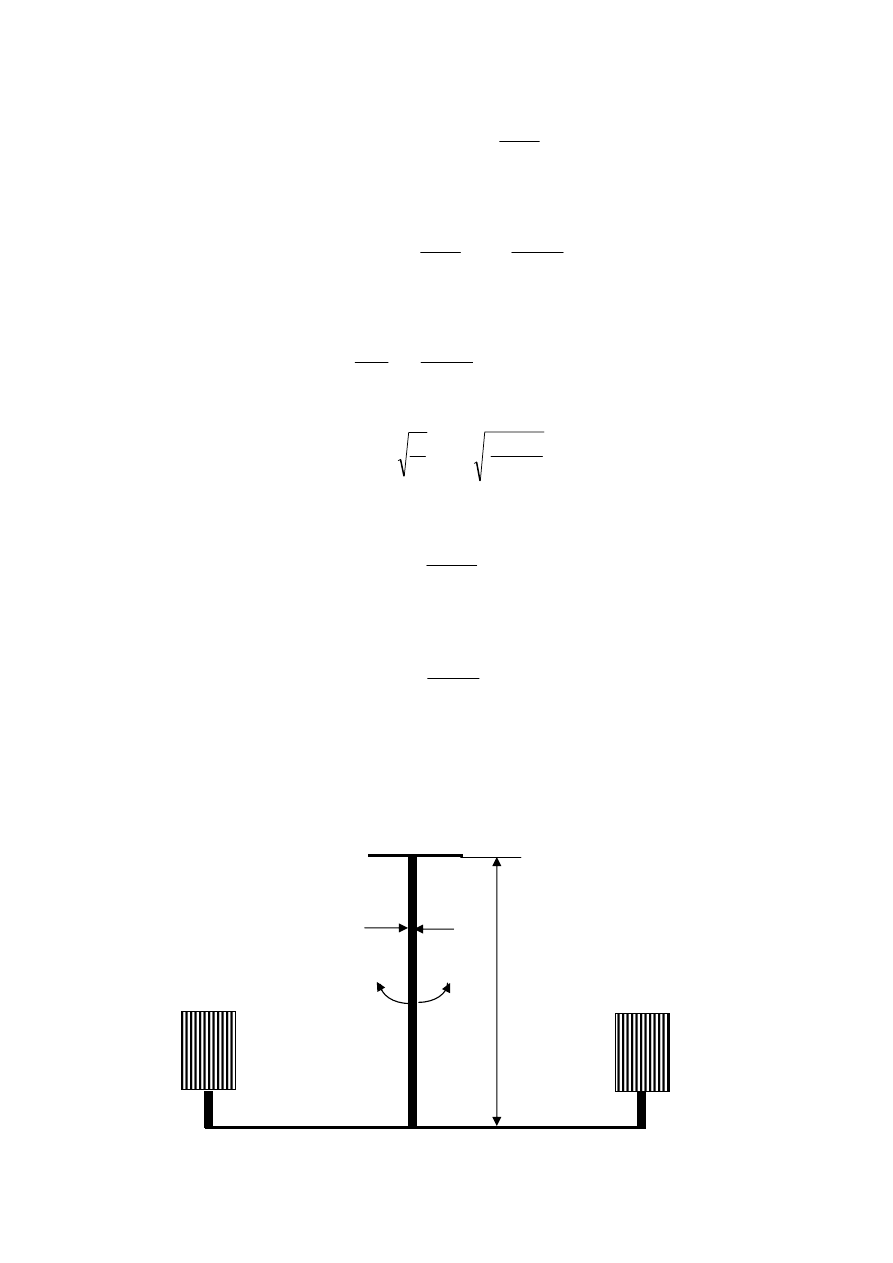
Powierzchnia ds. przekroju pierścienia ograniczonego obwodu o promieniu r

*

i r

*

+dr

*

wynosi

2

πr

*

dr

*

. Wartość siły stycznej działającej na taki pierścień wyraża się wzorem:

α

π

τ

l

r

dr

r

dS

dF

S

*

*

*

G

2

=

=

d r *

r *

l

d S

γ

α

a moment siły

*

3

*

*

)

(

G

2

dr

l

r

r

dF

dM

S

α

π

=

=

Całkując to wyrażenie w granicach od zera do r, otrzymamy wartość momentu siły działającej na
powierzchnię przekroju poprzecznego drutu

α

π

α

π

l

r

G

dr

l

r

M

r

2

)

(

G

2

4

0

*

3

*

=

=

∫

Drugą zasadę Newtona możemy dla tego przypadku zapisać w postaci

α

α

π

α

D

2

J

4

2

2

−

=

−

=

l

r

G

dt

d

stąd:

4

2

2

D

J

π

2

T

r

G

J

l

π

π

=

=

(40.3)

Mierząc okres T możemy wyznaczyć wartość modułu sprężystości:

4

2

8

r

T

J

l

G

π

=

(40.4)

Zależność między modułem skręcenia a modułem sprężystości wynika z zależności (40.3) i jest
następująca

l

r

G

D

2

4

π

=

(40.5)

40.2. Metoda pomiaru.

Obiektem badań jest pręt o długości

l i średnicy 2r, którego jeden koniec jest sztywno zamocowany

w części górnej drugi zaś jest poddawany działaniu sił skręcających (rys.40.3)

2r

M.

l

M

d

Rys.40.3. Wahadło torsyjne

W dalszej części pręta zamocowane jest ramie o długości 2d, na którego końcach znajdują się dwa
stanowiska do zamocowania walców wykonanych z trzech różnych materiałów i posiadających
różne masy (mosiądz, aluminium i plexiglas). Odchylony w płaszczyźnie poziomej układ wykonuje
drgania torsyjne. Taki układ nosi nazwę wahadła torsyjnego. Jest to jeden z przykładów wahadła
fizycznego. Jak w każdym wahadle fizycznym jego okres zależy od własnego momentu bezwładno-
ści (zależność 40.2).
Ze wzoru tego wynika, że dla wyznaczenia modułu skręcenia, a przez niego modułu sprężystości
wystarczy zmierzyć okres drgań wahadła i wyznaczyć jego moment bezwładności. Jednak bezpo-
średnie wyznaczenie momentu bezwładności jest dosyć trudne. Trudność tę można ominąć w na-
stępujący sposób: zmierzyć najpierw okres drgań T

0

bryły nie obciążonej o pewnym nieznanym

momencie bezwładności J

0

, a następnie zmierzyć okres T drgań bryły obciążonej dodatkowym cia-

łem o kształcie pozwalającym analitycznie obliczyć jego moment bezwładności J. Zapiszmy wzór
(40.2) dla obydwu wymienionych przypadków:

D

J

π

2

T

0

0

=

D

J

J

π

2

T

0

+

=

Proste przekształcenia pozwolą wyeliminować z tych dwóch równań wielkość J

0

i otrzymać wyra-

żenie dla modułu skręcenia:

2

0

2

2

4

T

T

J

D

−

=

π

(40.6)

Po podstawieniu ostatniego wzoru do zależności (40.5) powstanie wyrażenie dla modułu sprężysto-
ści:

)

(

8

2

0

2

4

T

T

r

J

l

G

−

=

π

(40.7)

Należy jeszcze znaleźć kryterium stosowalności dla potrzeb ćwiczenia wzoru (40.2). Wzór ten jest
słuszny dla drgań nietłumionych, podczas gdy w rzeczywistości mamy do czynienia z drganiami
tłumionymi. Jeśli jednak tłumienie jest nieduże, tzn. zmiana amplitudy w ciągu jednego okresu jest
znacznie mniejsza od bezwzględnej wartości amplitudy, to wzór (40.2) można stosować jako dobre
przybliżenie . Kryterium jego stosowalności może służyć nierówność

1

〉〉

n

(40.8)

gdzie n oznacza liczbę pełnych drgań, po wykonaniu których amplituda zmniejszy się np. dwa razy.
Na zakończenie należy jeszcze zauważyć, że okres T, jak wynika to ze wzoru (40.2), nie zależy od
amplitudy. Jednak przy dużych amplitudach prawo Hooke nie jest spełnione i okres T może zależeć
od amplitudy. W związku z tym, drugim warunkiem stosowalności wzoru (40.2) jest zachowanie
równości

T

=

const

(40.9)

którą można łatwo sprawdzić eksperymentalnie.

40.3. Wykonanie pomiarów.

Celem niniejszego ćwiczenia jest wyznaczenie modułu skręcenia D pręta a następnie obliczenie
modułu jego sprężystości G.
W ćwiczeniu tym wykorzystywane są trzy dodatkowe obciążenia w postaci walców wykonanych z
różnych materiałów. W przypadku, gdy na konstrukcję wahadła nałożone są symetrycznie dwa wal-
ce o jednakowej masie m to (przy założeniu, że ramie wahadła d jest znacznie większe niż wymiary
walców, co w układzie laboratoryjnym jest spełnione) zmiana momentu bezwładności wyniesie:

J = 2 m d

2

(40.10)

Masy walców oraz parametry geometryczne wahadła oraz ich średnie błędy kontrastowe są podane
przy ćwiczeniu.
Kolejność pomiarów jest następująca:
1. Zapoznać się z budową wahadła torsyjnego.
2. Ustalić zakres amplitudy, w którym spełniony jest warunek (40.9). W tym celu należy umieścić

wybraną parę walców na wahadle i wzbudzić przy pomocy pary sił drgania torsyjne zadając
pewną początkową amplitudę.Mierząc czas 10 pełnych wahnień, określić okres T

1

. Zmniejszyć

amplitudę i tym samym sposobem wyznaczyć T

2

. Jeśli okaże się, że T

1

≠

T

2

to należy zmniej-

szyć amplitudę do takiej wartości

Φ, zaczynając od której dla wszystkich φ < Φ będzie wypeł-

niona równość T

1

= T

2

.

3. Sprawdzić sprawiedliwość nierówności (40.8) dla wahadła używanego w niniejszym ćwiczeniu.
4. Zmierzyć dziesięciokrotnie przymiarem długość ramienia d.
5. Wprawić w drgania torsyjne (amplituda drgań nie większa od ustalonej na początku pomiarów)

wahadło nie obciążone walcami i zmierzyć czas trwania 10 okresów T

0

. Pomiar powtórzyć co

najmniej 10 razy.

6. Powtórzyć pomiary wg punktu 5 dla wahadła obciążonego walcami: z plexiglasu, aluminium i

mosiądzu. Wyznaczone okresy oznaczyć odpowiednio: T

PL

, T

AL

, T

M

.

7. Wyniki wszystkich pomiarów przedstawić w formie tabeli.

40.4 Opracowanie wyników pomiarów.

1. Z otrzymanych pomiarów obliczyć średnią arytmetyczną d

Śr

i średni błąd kwadratowy

Śr

d

σ

2. Obliczyć momenty bezwładności J dla 3 materiałów i błędy na nich.
3. Obliczyć średnie arytmetyczne okresów drgań: T

0

, T

PL

, T

AL

, T

M

i ich średnie błędy kwadratowe.

4. Wykorzystując obliczone średnie znaleźć wartości modułu skręcenia D i modułu sprężystości G

ze wzorów (40,6) (40,7) dla 3 przypadków. Wyniki obliczeń podać w układzie SI

5. Obliczyć średnie błędy kwadratowe na wyznaczonych wartościach D i G.
6. Zestawić otrzymane wyniki i wyciągnąć wnioski.

40.5. Pytania kontrolne

1. Opisz drgania wahadła torsyjnego.
2. Opisz mechanizm skręcania pręta.

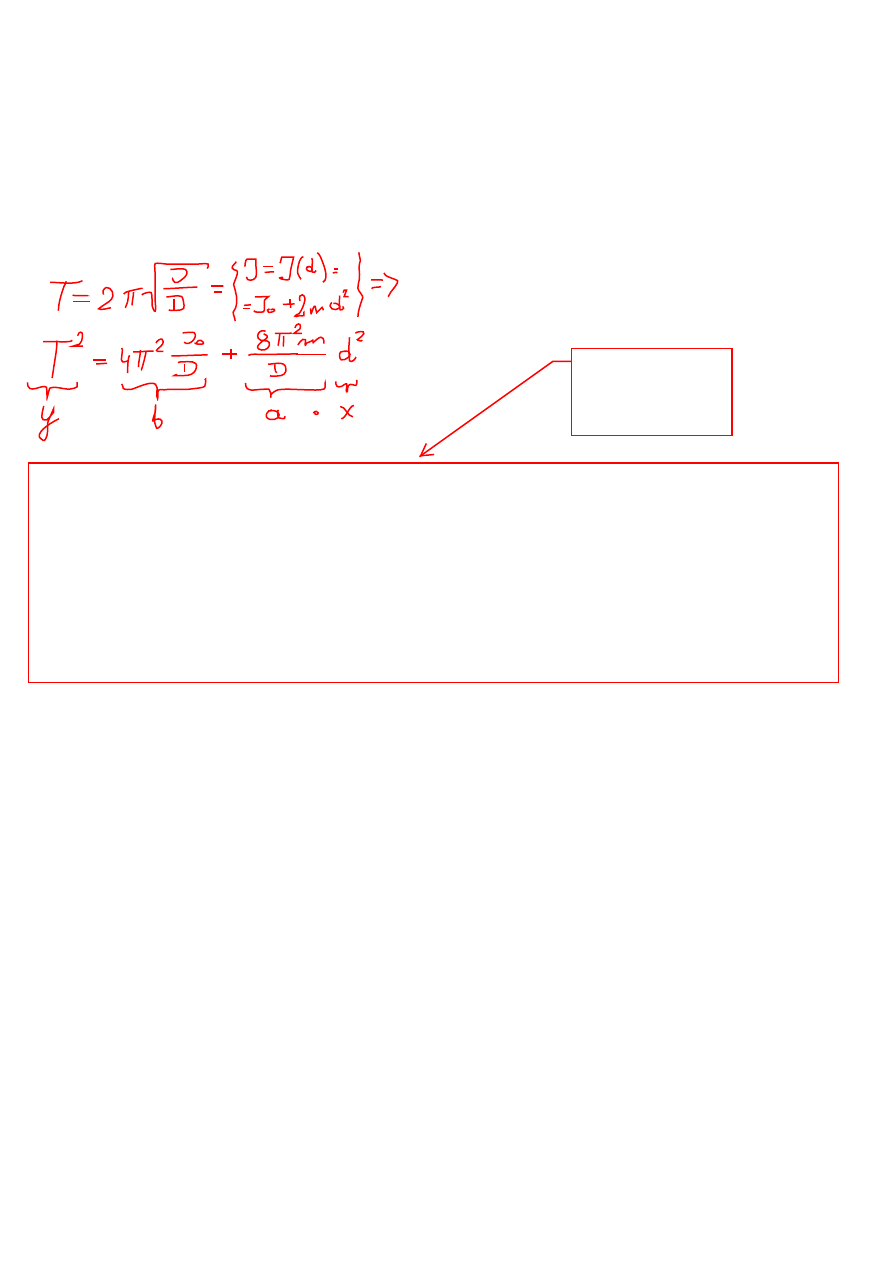
3. Wyprowadź wzór na moment siły skręcającej pręt i moment sprężystości.
4. Podaj twierdzenie o osiach równoległych (Steinera). Czy ma ono zastosowanie w ćwiczeniu?

L i t e r a t u r a

[2] Kittel.C. , Knight W.D. , Ruderman M.A.:Mechanika. PWN W-wa 1973r.

Opracowanie:
1. Wykres y=ax+b (T

2

=b+ad

2

).

2. Wyzanczenie warto

ś

ci a i b z metody najmniejszych kwadratów.

3. Wyznaczenie warto

ś

ci D z a.

4. Wyznaczenie wartosci J

0

z b.

5. Wyznacznie G.
6. Wyznaczenie modu

ł

u Younga z G.

7. Analiza b

łę

dów z matody najmniejszych kwadratów Gaussa i z metody przenoszenia sie b

łę

dów.

8. Zebra

ć

wyniki i ich niepewno

ś

ci w ca

ł

o

ść

i porówna

ć

z danymi z literatury. Omówi

ć

jako

ść

metody

i wyci

ą

gn

ąć

wnioski.

W paktyce robimy
tylko jeden materia

ł

(chyba jaki

ś

stop

aluminium ?).