Fizyka Ciała Stałego II
opracowanie zagadnień
1. Ciepło właściwe wg Debye’a.
Ciepło właściwe, powtórka:
Gaz doskonały, jednoatomowy:
ciepło właściwe przy stałej objętości
R
c
V
2
3
=
ciepło właściwe przy stałym ciśnieniu
R
c
p
2
5
=
- wyniki, które chcemy wyprowadzić.
Dla 1 mola gazu:
R
T
pV
=
Rozważmy gaz w sześciennym pudle o krawędzi l . Możemy rozpatrywać oddzielnie każdą cząstkę.
Jeśli prędkość danej cząstki w jednym kierunku, np. w kierunku y , wynosi
y
v
, to
czas między kolejnymi uderzeniami o ściankę:
y
v
l
t
2
=
.
Zmiana pędu w jednorazowym akcie zderzenia:
y
mv
p
2
=
∆
Siła:
dt
p
d
dt
v
d
m
a
m
F
=
=
=
, stąd siła działająca na ścianki:
l
mv
v
l
mv
t
p
F
y
y
y
2
2
2
=
=
∆
=
Ciśnienie, jakie wywiera jedna cząsteczka na ścianki naczynia:
V
mv
l
mv
l
F
p
y
y
2
3
2
2
=
=
=
Gdy weźmiemy dużo cząstek:
ś
rednia prędkość:
2
2
2
2
z
y
x
ś
r
v
v
v
v
+
+
=
z
y
x
v
v
v
=
=
→
2
2
2
2
3
1
ś
r
z
y
x
v
v
v
v
=
=
=
Ciśnienie całkowite jednego mola:
V
mv
N
p
A
cał
3
2
=
2
3
1
mv
N
V
p
A
cał
=
1
2
2
k
E
mv
=
- energia kinetyczna 1 cząsteczki
U
E
E
N
V
p
cał
k
k
A
cał
3
2
3
2
3
2
,
1
=
=
=
Ze wzoru
R
T
pV
=
→
RT
pV
=
RT
U
=
3
2
→
RT
U
2
3
=
Ciepło właściwe to ilość energii, jaką musimy dostarczyć, aby ogrzać ciało o 1°C:
R
T
U
V
2
3
=
∂
∂
A co będzie, jeśli zmienimy objętość, np. przesuwając tłok o powierzchni S o x
∆
?
Praca wykonana podczas przesuwania tłoka:
V
p
x
S
p
x
F
W
∆
⋅
=
∆
⋅
⋅
=
∆
⋅
=
p
RT
V
=
p
RT
V
1
1
=
p
RT
V
2
2
=
→
(
)
T
R
T
T
p
R
p
V
p
W
∆
⋅
=
−
=
∆
⋅
=
1
2
Stąd dodatkowa praca wykonana kosztem dostarczonego ciepła na rozprężenie gazu:
R
T
W
=
∆
∆
R
R
R
T
U
p
2
5
2
3
=
+
=
∂
∂
Ciepło właściwe dla ciał stałych (prawo Doulonge’a – Petitte’a) :
R
T
U
V
3
=
∂
∂
Zależność ciepła właściwego od temperatury jest jak
3
T . Próbował to wyjaśnić najpierw Einstein, który
założył, że drgania sieci są skwantowane. Jego teoria dobrze sprawdzała się w pewnym zakresie
temperatur, jednak uwzględniała tylko drgania optyczne, podczas gdy w niskich temperaturach
dominują drgania akustyczne.
W pełni wyjaśnił tą zależność Debye, który założył liniową zależność częstości od wektora falowego.
Rozważmy wielkość zależną od temperatury. Temperatura wynika z drgań fononów o częstości
ω
od 0 do
max
ω
:
ω
ω
ω
ω
ω
d
Z
f
A
T
A
⋅
⋅
⋅
=
∫
)
(
)
(
)
(
)
(
| |
prawdopodobieństwo gęstość
obsadzenia stanu
o danej częstości
N
d
Z
3
)
(
max
0
=
⋅
∫
ω
ω
ω
- ilość drgań zależnych od wektora falowego dla fononów
Oznaczenie wektora falowego: elektrony -
k
, fonony - q
π
π
8
1
)
2
(
1
)
(
3
=
=
q
Z
- podobnie jak dla elektronów, tylko 2 razy mniej, bo bez spinów (dla
1
=
V
)
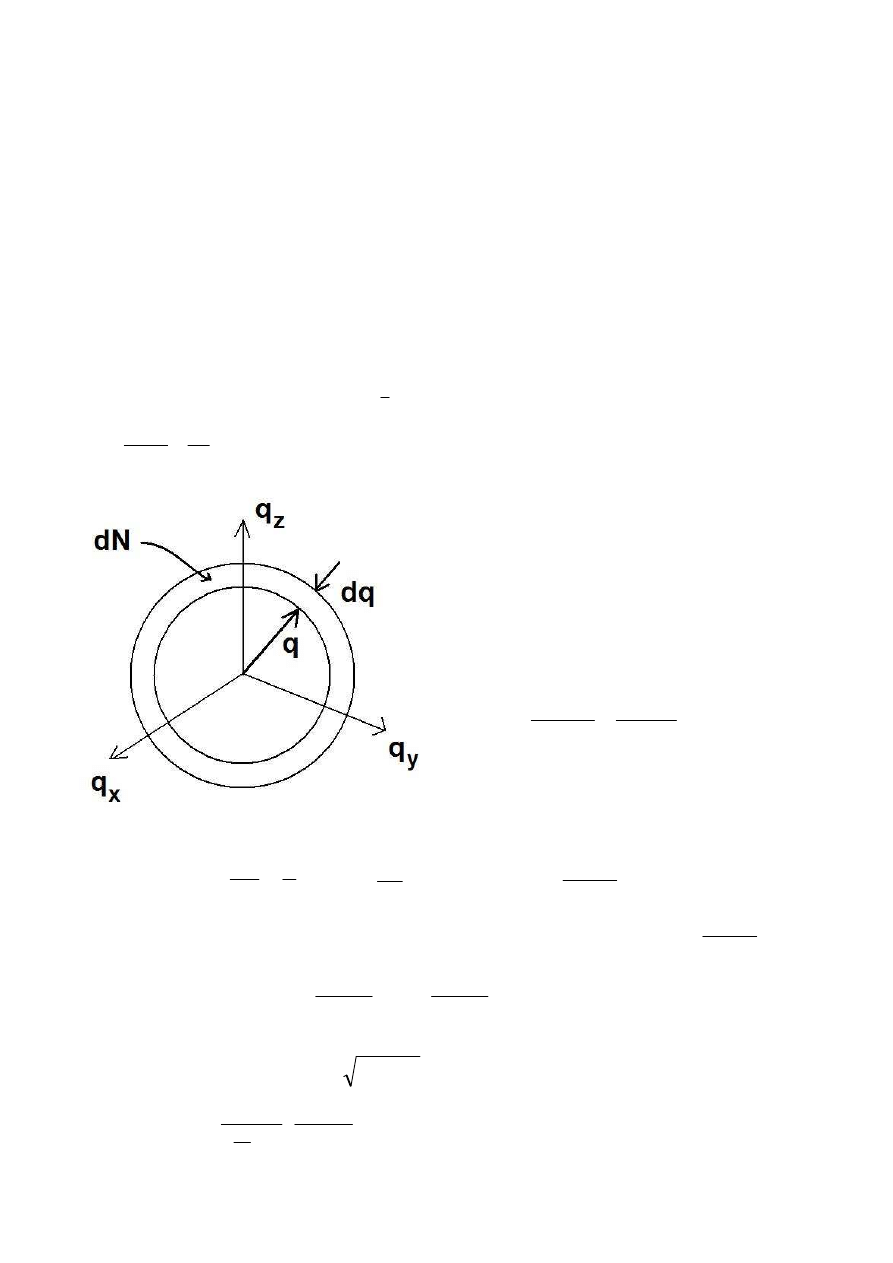
Fala stojąca w ciele stałym jest skwantowana
(mamy skończoną ilość możliwych długości fali)
– długość fali jest ograniczona od góry przez
rozmiary kryształu, a od dołu przez odległość
między atomami.
ω
ω
π
d
Z
dq
q
q
Z
dN
⋅
=
⋅
=
)
(
4
)
(
1
2
1
(dla jednej gałęzi drgań)
ω
π
ω
π
π
ω
d
dq
q
d
dq
q
Z
2
2
3
2
1
2
8
4
)
(
=
=
Debye założył, że częstość jest zależna liniowo od
wektora falowego, a współczynnikiem
proporcjonalności jest prędkość dźwięku.
q
u
⋅
=
ω
→
u
d
dq
1
=
ω
,
2
2
2
u
q
ω
=
, stąd:
3
2
2
1
2
)
(
u
Z
π
ω
ω
=
Powyższy wynik dotyczy jednej gałęzi. A więc całkowita gęstość:
3
2
2
1
2
3
)
(
3
)
(
u
Z
Z
π
ω
ω
ω
=
⋅
=
N
d
Z
3
)
(
max
0
=
⋅
∫
ω
ω
ω
→
A
N
u
d
u
3
2
2
3
3
2
3
max
0
3
2
2
max
=
=
⋅
∫
π
ω
ω
π
ω
ω
- wstawiamy tu liczbę Avogadro
(liczymy ciepło molowe)
A
N
u
3
2
3
max
6
π
ω
=
→
u
N
A
⋅
=
3
2
max
6
π
ω
∫
⋅
−
⋅
=
max
0
3
2
2
2
3
1
1
)
(
)
(
ω
ω
ω
π
ω
ω
d
u
e
A
T
A
kT
h
|
statystyka Bosego-Einsteina (fonony są bozonami)
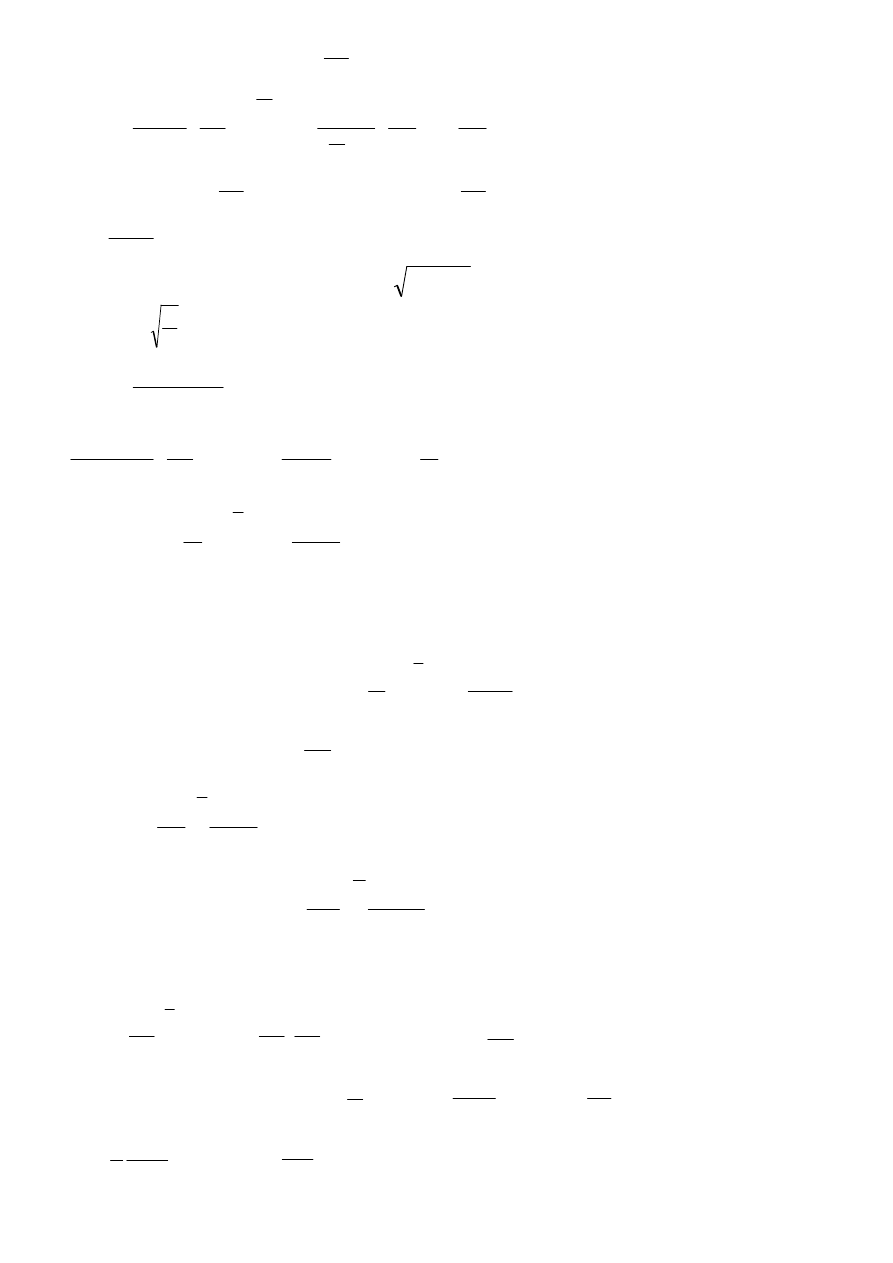
Bierzemy zmienną do całkowania:
kT
ω
h
−
⋅
=
∫
kT
d
kT
e
A
kT
u
T
A
kT
kT
ω
ω
ω
π
ω
ω
h
h
h
h
h
0
2
3
3
2
1
1
)
(
2
3
)
(
Debye zauważył, że
k
ω
h
ma wymiar temperatury (bo
kT
ω
h
jest bezwymiarowe)
stąd:
Θ
=
k
max
ω
h
- tzw. temperatura Debye’a
max
ω
zależy od prędkości dźwięku:
u
N
A
⋅
=
3
2
max
6
π
ω
z kolei
m
u
α
~
, gdzie
α
- stała sprężystości
A
N
u
2
3
max
3
6
π
ω
=
- wstawiamy to do wyrażenia przed całką:
3
3
max
3
3
max
2
2
9
9
2
6
3
Θ
=
=
⋅
T
N
kT
N
kT
N
A
A
A
h
h
ω
ω
π
π
, a stąd:
x
d
e
x
A
T
N
T
A
T
x
A
∫
Θ
−
⋅
Θ
=
0
2
3
1
)
(
9
)
(
ω
- jest to wzór odnoszący się do wszystkich materiałów
Możemy policzyć średnią energię:
energia 1 fononu:
ω
ω
h
=
)
(
A
ś
rednia energia:
x
d
e
x
A
T
N
U
T
A
T
x
A
∫
Θ
−
⋅
Θ
=
=
0
2
3
1
)
(
9
)
(
ω
ω
h
zauważamy, że:
kTx
kT
kT
=
=
ω
ω
h
h
x
d
e
x
T
kN
U
T
x
A
∫
Θ
−
⋅
Θ
=
0
3
3
4
1
9
,
R
kN
A
=
Ostatecznie:
x
d
e
x
T
R
U
T
x
∫
Θ
−
⋅
Θ
=
0
3
3
4
1
9
Rozwiązanie analityczne:
1° wysokie temperatury:
Θ
>>
T
,
1
<<
x
,
1
max
<<
x
,
x
x
e
x
=
−
+
≈
−
1
1
1
RT
T
T
R
x
d
x
T
R
U
T
3
9
9
3
3
3
4
0
2
3
4
=
Θ
⋅
Θ
=
⋅
Θ
=
∫
Θ
,
R
T
U
c
V
3
=
∂
∂
=
2° niskie temperatury:
Θ
<<
T
→
∞
→
Θ
T
,
const
x
d
e
x
x
=
=
−
∫
∞
15
chyba
1
2
0
3
π
Θ
≅
4
5
3 RT
U
,
3
~ T
T
U
c
V
∂
∂
=
- pojawia się zależność, którą wcześniej otrzymano
Dla elektronów w metalach:
T
c
V
~
.