2. WSTĘP DO TEORII SPRĘŻYSTOŚCI

1

2.



2. WSTĘP DO TEORII SPRĘŻYSTOŚCI

2.1. Tensory macierzy

Niech macierz [D] będzie macierzą cosinusów kierunkowych

[

D

]

=

[



i ' j

]

(2.1)

Macierz transformowana jest równa macierzy odwrotnej (transformacja ortonormalna)

[

D

]

−1

=

[

D

]

T

(2.2)

Jeśli przyjmiemy, że wektor w pierwszej bazie ma współrzędne A

i

a w drugiej bazie współrzędne A

i'

to możemy macierzowo zapisać

[

A

i '

]

=

[

D

]

[

A

i

]

(2.3)

Postać macierzową można utworzyć także dla tensora

T

ij

=[T ]

3

×3

(2.4)

jak i wektora

A

i

=[ A]

3

×1

={A}=col [ A]=col {A}

(2.5)

Zauważmy, że transponując wektor w rezultacie otrzymamy macierz o wymiarach 1x3

{A}

T

=[ A]

1

×3

(2.6)

Mnożenie skalarne przedstawia się za pomocą zapisu

a) skalarnego (absolutnego)

A⋅B=c

(2.7)

b) wskaźnikowego

c

=A

i

⋅B

i

(2.8)

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

2. WSTĘP DO TEORII SPRĘŻYSTOŚCI

2

c) macierzowego

A→[ A]=

[

A

1

A

2

A

3

]

=[ A

1

A

2

A

3

]

T

B →[B]=

[

B

1

B

2

B

3

]

[

B

1

B

2

B

3

]

3

×1

A⋅B=[ A]

T

[ B]=[ A

1

A

2

A

3

]

1

×3

[C ]

(2.9)

Łatwo zatem zauważyć, że w wyniku mnożenia dwóch macierzy o wymiarach 3x3 otrzymujemy

macierz także o wymiarach 3x3. Pamiętajmy o tym, że mnożenie dwóch macierzy jest możliwe tylko wtedy,
gdy liczba kolumn pierwszej z nich jest równa liczbie wierszy drugiej.

[ A]

3

×3

[ B]

3

×3

=[C ]

3

×3

(2.10)

Wskaźnikowo mnożenie dwóch macierzy 3x3 zapisujemy w następujący sposób:

A

ij

⋅B

jk

=C

ik

(2.11)

2.2. Działanie tensora na wektor

Tensor działa na wektor jako operator

T a=b

T

ij

a

j

=b

i

[T ]

3

×3

[a]

3

×1

=[b]

3

×1

(2.12)

co przedstawiają powyższe równania w zapisie odpowiednio absolutnym, wskaźnikowym i

wektorowym. Działanie tensora można przykładowo zaprezentować w następujący sposób:

a⋅T =c

[a]

3

×1

[T ]

3

×3

 niewykonalne

a

i

⋅T

ij

=c

j

[a]

1

×3

T

[T ]

3

×3

=[b]

1

×3

T

A

i '

=

i ' j

A

j

[ A

'

]=[ D][ A]

A

j

=

ji '

A

i '

[ A]=[ D]

T

[ A

'

]

(2.13)

2.3. Transformacja tensora (o 9 składowych)

Korzystając z prawa transformacji tensora wyznaczymy teraz współrzędne tensora w układzie

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

2. WSTĘP DO TEORII SPRĘŻYSTOŚCI

3

obróconym. Postać macierzową wektora

b

w układzie pierwotnym możemy przedstawić jako

[b]=[T ][a]

(2.14)

natomiast w układzie obróconym

[b

'

]=[T

'

][a

'

]

(2.15)

Szukany tensor w układzie obróconym wyznaczamy w następujący sposób:

[b

'

]=[ D][b]

[b]=[ D]

T

[b

'

]

[a]=[ D]

T

[a

'

]

(2.16)

podstawiamy do wzoru

[b]=[T ][a]

i otrzymujemy

[ D]

T

[b

'

]=[T ][ D]

T

[a

'

]

[b

'

]=[T ][ D][ D]

T

[a

'

]

[b

'

]=[T

'

][a

'

]

[T

'

]=[ D][T ][ D]

T

(2.17)

2.4. Analiza pól

Funkcja wektorowa – funkcja, która każdemu punktowi przestrzeni przyporządkowuje wektor.

Funkcja tensorowa – funkcja, która każdemu punktowi przestrzeni przyporządkowuje tensor.

Funkcja skalarna – funkcja, która każdemu punktowi pewnego obszaru przyporządkowuje okreslony

skalar (zwana także polem skalarnym).

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

2. WSTĘP DO TEORII SPRĘŻYSTOŚCI

4

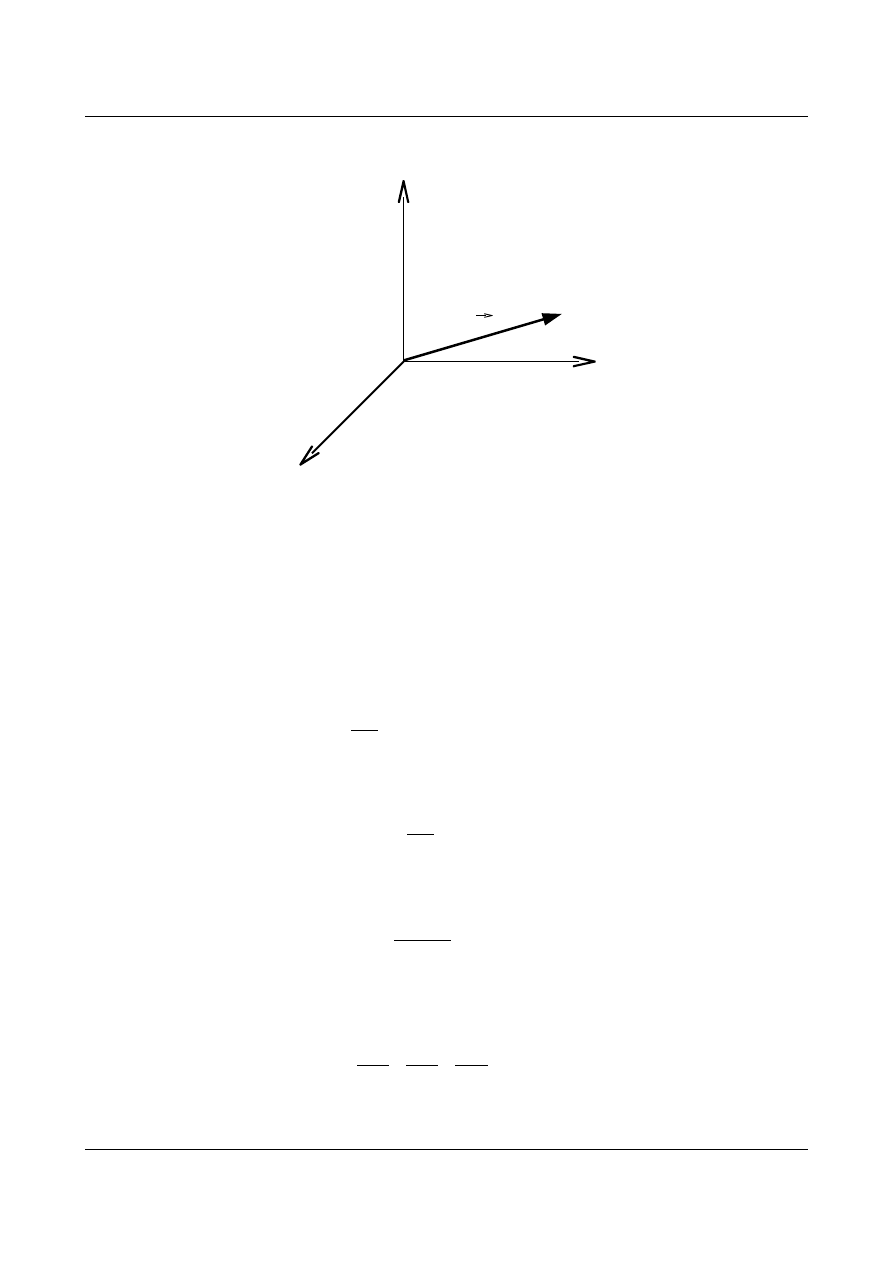
1) Gradient - funkcja wektorowa.

Rys. 2.1. Wektor

X

w układzie kartezjańskim.

X

- zapis absolutny

X

i

- zapis wskaźnikowy

[

X

]

3

×1

- zapis macierzowy

Funkcja

 x

1

, x

2

, x

3



jest funkcją skalarną. Jeżeli przyjmiemy, że pochodne tej funkcji są

współrzędnymi pewnego wektora to wektor ten nazywamy gradientem pola skalarnego. Różniczkujemy
funkcję po odpowiednich współrzędnych:

G

i

=

∂

∂ x

i

=G  x

1

, x

2

, x

3



(2.18)

Pierwsza pochodna funkcji:



,i

=

∂
∂ x

i

(2.19)

Druga pochodna:



,ij

=

∂

2



∂ x

i

∂ x

j

(2.20)

Różniczkowanie połączone z sumowaniem:



, ii

=

∂

2



∂ x

1

2



∂

2



∂ x

2

2



∂

2



∂ x

3

2

(2.21)

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

X

1

2

3

2. WSTĘP DO TEORII SPRĘŻYSTOŚCI

5

Wyznaczamy gradient funkcji:



G

=G

1

e

1

G

2

e

2

G

3

e

3

=G

i

e

i

=

∂
∂ x

i

e

i

=

,i

e

i

=grad =

∇ 

(2.22)

A więc ostatecznie gradient funkcji



G

=

∇ 

(2.23)

gdzie operator Nabla



∇≡ ∂

∂ x

i

e

i

(2.24)

Gradient określa kierunek i wartość przyrostu funkcji.

Zad.1. Znając prawo transformacji wektorów udowodnić, że wielkość zwana gradientem jest

wektorem.

G

i '

=

,i '

=

∂

∂ x

i '

=

∂

∂ x

j

∂ x

j

∂ x

i '

=

∂

∂ x

j



ji '

=

∂

∂ x

j



i ' j

=

i ' j

G

j

2) Diwergencja – każdemu punktowi odpowiada wektor:

A=A

i

e

i

gdzie

A

i

=A

i

 x

1

x

2

x

3

=A

i

 x

ii



T

ij

=

∂ A

i

∂ x

j

=A

i , j

(2.25)

Polem diwergencji różniczkowalnego pola wektorowego nazywamy pole skalarne okreslone

zależnością

A

i , j

= A

i ,i

=

∂ A

1

∂ x

1



∂ A

2

∂ x

2



∂ A

3

∂ x

3

=div A

(2.26)

Ta wielkość ma cechy tensora.

Zad.2. Udowodnić, że omawiana wielkość jest tensorem przez wykazanie, że

T

ij

transformuje się

według prawa transformacji tensora.

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

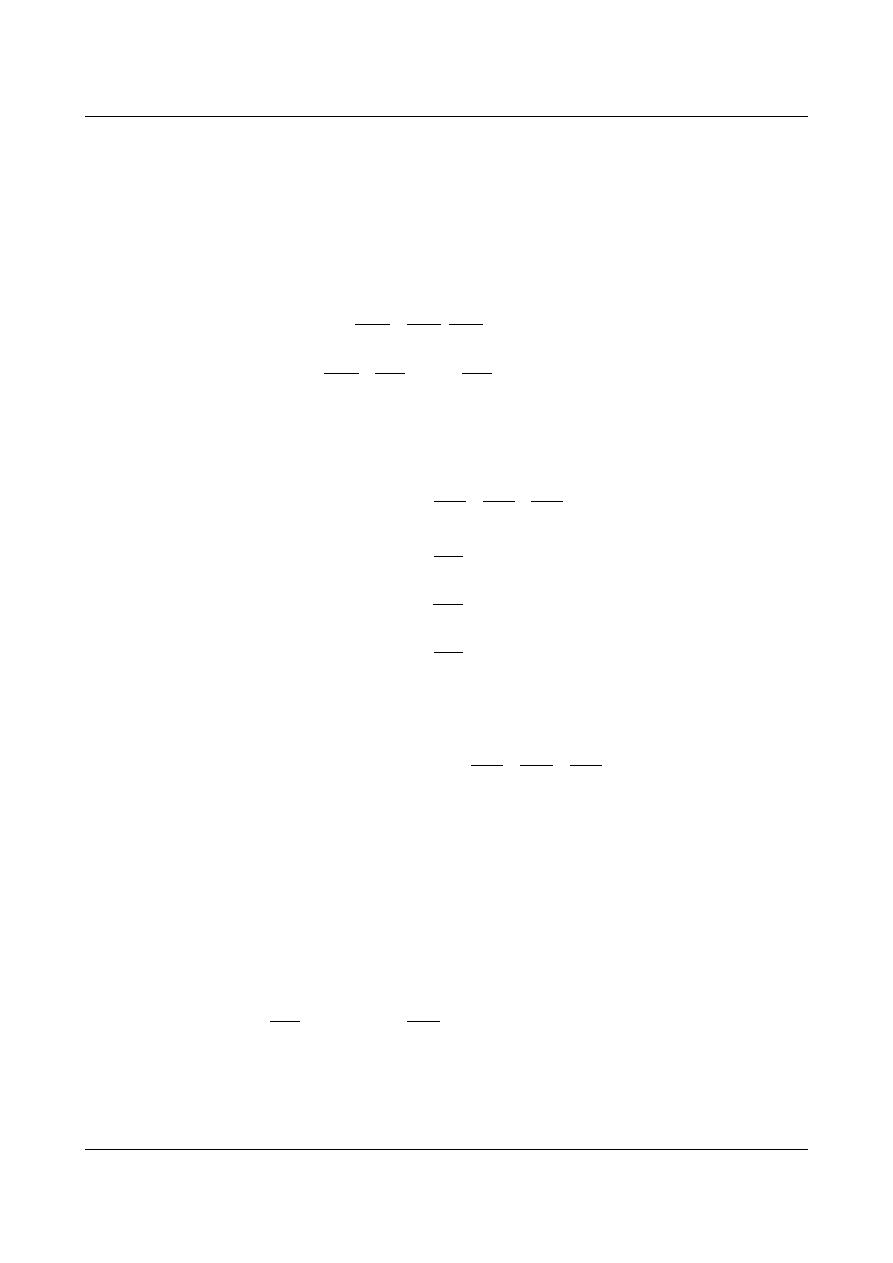
2. WSTĘP DO TEORII SPRĘŻYSTOŚCI

6

A=

[

A

1

A

2

A

3

]

T

ij

=

[

A

1,1

A

1,2

A

1,3

A

2,1

A

2,2

A

2,3

A

3,1

A

3,2

A

3,3

]

T

ij

=A

i , j

A

i ' , j '

=

∂ A

i '

∂ x

j '

=

∂ A

i '

∂ x

k

⋅

∂ x

k

∂ x

j '

=A

i ' , k



kj '

=☼

A

i , ' k

=

∂ A

i '

∂ x

k

= ∂

∂ x

k

 A

i ,'

= ∂

∂ x

k

 A

i



i ' i

=A

i , k



i ' i

☼

=A

i ' k



j ' k



i ' k

Zad.3. Czy jest możliwe zapisanie diwergencji macierzowo?

div 

A

=

∇⋅A=

∂ A

1

∂ x

1



∂ A

2

∂ x

2



∂ A

3

∂ x

3



∇⋅A=

[

∂

∂ x

1

∂

∂ x

2

∂

∂ x

3

]

T

⋅

[

A

1

A

2

A

3

]

Zad.4. Obliczyć div z gradΦ.

div

grad =div[

, i

e

i

]=

, ii

=

∂

2



∂ x

1

2



∂

2



∂ x

2

2



∂

2



∂ x

3

2

=∇

2



∇

2



Laplasjan funkcji skalarnej

3) Rotacja – polem rotacji różniczkowalnego pola wektorowego

A

nazywamy pole wektorowe określone

zależnością



∇×A=rot A=R

∂

∂ x

j



e

j

×A

k



e

k

=e

ijk

∂ A

u

∂ x

j

e

i

=e

ijk

A

k , j

e

i



e

j

× 

e

k

= 

e

ijk

e

i

R

=e

ijk

A

k , j

(2.27)

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

2. WSTĘP DO TEORII SPRĘŻYSTOŚCI

7

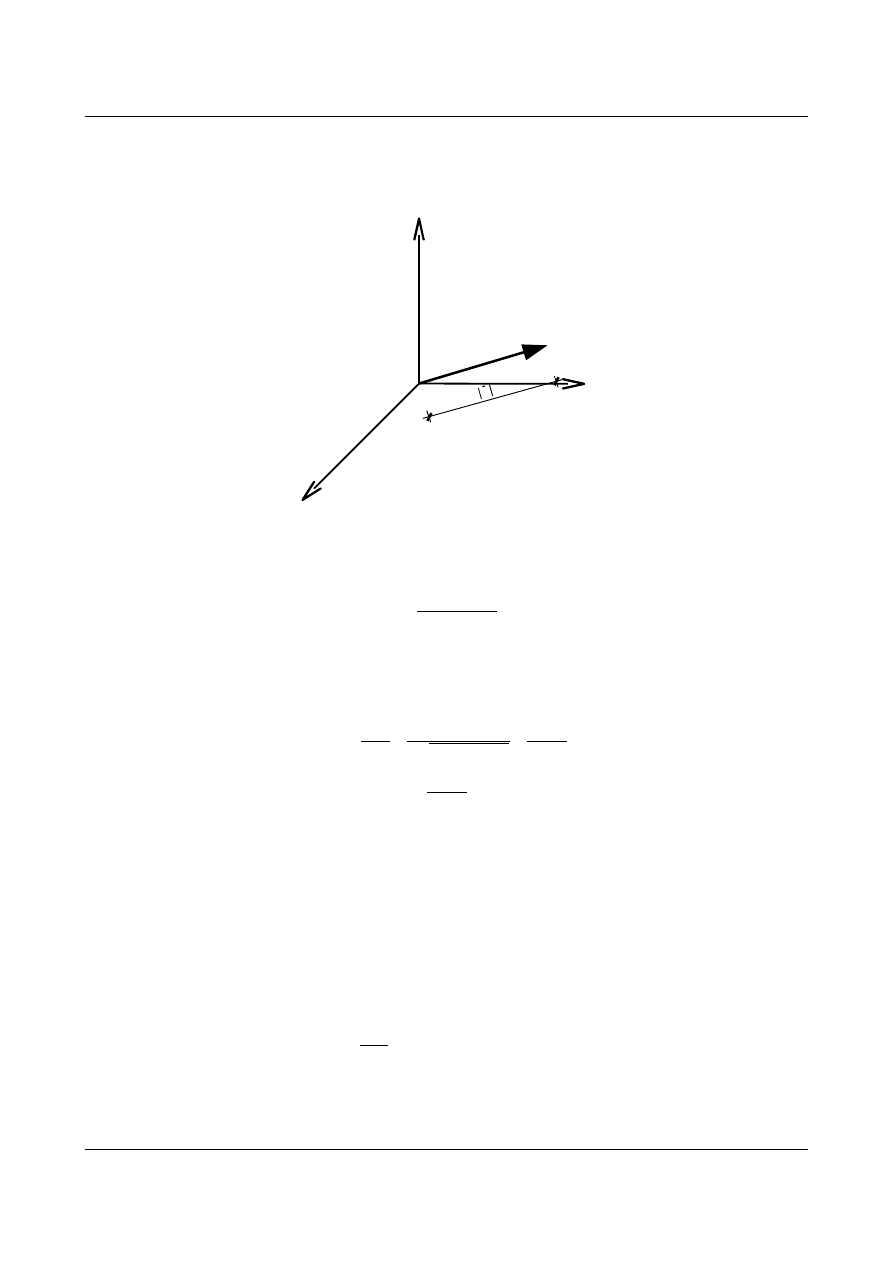
Przykład:

Dany jest punkt P.

Funkcją opisującą położenie tego punktu jest funkcja

x

1

x

2

x

3



opisana wzorem

=



x

1

2

x

2

2

x

3

2

a) wyznaczyć gradient tej funkcji

G

i

=

,i

G

1

=

∂

∂ x

1

=

1

⋅2 x

1

2



x

1

2

x

2

2

x

3

2

=

x

1

│

r │



G

= 

r

│

r │

= e

r

b) Obliczyć div

r

gdy dane są współrzędne wektora miejsca

r

:

r

1

=x

1

r

2

=x

2

r

3

=x

3

r=x

i

e

i

∂

∂ x

i

e

i

⋅x

i

e

i

=111=3

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

3

2

1

r

P

2. WSTĘP DO TEORII SPRĘŻYSTOŚCI

8

c) Obliczyć rotację wektora

r

∂

∂ x

i

e

i

×x

i

e

i

=

∂ x

i

∂ x

i

e

i

×e

i

=0

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater