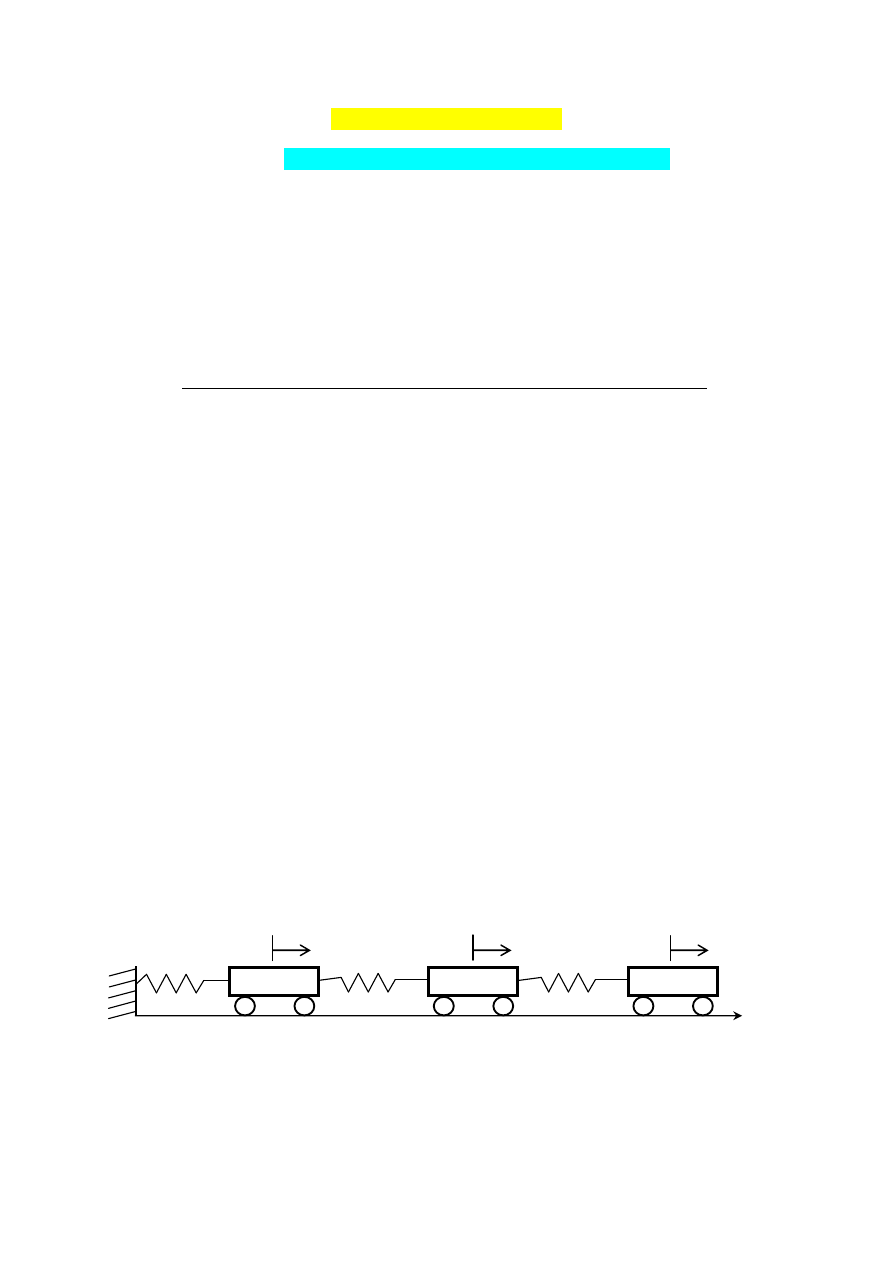
PRZYKLAD OBLICZENIOWY nr 4
Temat : Rozwiązywanie problemu wartości własnych Ax=λx
Wymagane obliczenia należy przeprowadzić “ręcznie” (tj. używając “kalkulatora” a nie gotowego
programu generującego ostateczny wynik).
Każdy student rozwiązuje inny przykład liczbowy, oznaczony numerem odpowiadającym numerowi
nazwiska studenta na liście. Każda grupa laboratoryjna ma oddzielny zestaw zadań (przykłady
zamieszczone są w dalszej części, po opisie zadań do wykonania).
W przypadku problemów obliczeniowych proszę skontaktować sie z prowadzącym zajęcia.
Podpisany konspekt z wynikami obliczeń i wnioskami należy oddać prowadzącemu zajęcia
przed laboratorium poświęconym rozwiązywaniu układów równań liniowych.
Zadanie 1:
Obliczanie analityczne wartości własnych
Wyznaczyć analitycznie wartości i wektory własne macierzy A (podanej w dalszej części).
Wartości własne obliczamy szukając zerowego wyznacznika macierzy Ax-λI , odpowiadające im
wektory własne obliczamy z zależności Ax=λx.
Zadanie 2: Obliczanie numeryczne wartości własnych - metoda potęgowa
Dla tego samego przykładu wykonać 5 iteracji metody potęgowej startując z wektora
początkowego x
0
=[1 1] (lub innego, jeśli ten nie jest odpowiedni). Dla każdego kroku podać
przybliżenie wartości własnej λ
i
(tutaj: o największym module) i odpowiadającego jej wektora
własnego x
i
. Przybliżenia wektorów własnych proszę normalizować korzystając z normy euklidesowej
(normy “2”) lub "nieskończonej". Czy obserwujemy zbieżność do rozwiązania analitycznego?
Zadanie 3: Przykład zagadnienia na wartości własne w mechanice
Rozważamy przedstawiony na rysunku układ trzech mas połączonych sprężynami:
Symbolami x1(t), x2(t) i x3(t) oznaczono oscylacje poziome mas m1, m2 i m3 (w funkcji czasu t)
wokół położenia równowagi, k1, k2 i k3 są współczynnikami sprężystości sprężyn.
x1(t)
x2(t)
x3(t)
m1
m2
m3
k1
k2
k3
x

Układ różniczkowych równań ruchu (w przypadku braku tłumienia) można zapisać w postaci:
''
0
3
''
0
3
3
''
0
k1+ k2
-k2
0
x1(t)
m1
0
0
x1 (t)
-k2
k2+ k3
k
x2(t)
0
m2
0
x2 (t)
0
k
k
x3(t)
0
0
m3
x3 (t)
−
+
=
−
gdzie x1″(t), x2″(t) i x3″(t) oznaczają drugie pochodne x1(t) , x2(t) i x3(t) po czasie.
Poszukujemy częstości własnych i postaci drgań własnych rozważanego układu, czyli niezerowego
rozwiązania powyższego układu równań różniczkowych. Zakładamy, że funkcje x1(t), x2(t) i x3(t),
spełniające równania ruchu, mają postać:
sin(
),
sin(
),
(
sin(
)
x1(t)
a1
t
x2(t)
a2
t
x3 t)
a3
t
ω θ
ω θ
ω θ
=
+
=
+
=
+
,
gdzie a1, a2, a3,
ω
i
θ
są stałymi niezależnymi od czasu.
Podstawiając x1(t) , x2(t) i x3(t) do równań ruchu wykazać, że
ω
2
jest wartością własną macierzy A
natomiast wektor własny tej macierzy ma składowe x=[a1 a2 a3]
T
.
(k1+ k2)/m1
-k2/m1
0
-k2/m2
(k2 + k3)/m2
-k3/m2
0
-k3/m3
k3/m3
=
A
GRUPA 1
Uwaga: każdy student wybiera dane zestawu o numerze odpowiadającym swojemu numerowi z listy
(patrz numeracja w załączonym pliku z obecnością na pierwszym laboratorium)
Nr przykładu
Macierz A
wartości własne
1
- 5. 3.
3. - 5.
- 8. 0.
0. - 2.
2
8. 6.
6. 8.
2. 0.
0. 14.
3
2. 5.
5. 2.
- 3. 0.
0. 7.
4
7. 6.
6. 7.
1. 0.
0. 13.
5
7. 11.
11. 7.
- 4. 0.
0. 18.
6
- 7. - 12.
- 12. - 7.
- 19. 0.
0. 5.
7
2. 15.
15. 2.
- 13. 0.
0. 17.
8
- 6. 3.
3. - 6.
- 9. 0.
0. - 3.
9
12. 9.
9. 12.
3. 0.
0. 21.
10
4. 5.
5. 4.
- 1. 0.
0. 9.
11
8. - 6.
- 6. 8.
2. 0.
0. 14.
12
- 2. - 6.
- 6. - 2.
- 8. 0.
0. 4.
13
- 12. 6.
6. - 12.
- 18. 0.
0. - 6.
14
1. 3.
3. 1.
- 2. 0.
0. 4.
15
- 2. 6.
6. - 2.
- 8. 0.
0. 4.
16
- 9. 3.
3. - 9.
- 12. 0.
0. - 6.
17
2. 6.
6. 2.
- 4. 0.
0. 8.
18
- 4. 11.
11. - 4.
- 15. 0.
0. 7.
19
- 3. 5.
5. - 3.
- 8. 0.
0. 2.
20
- 1. 6.
6. - 1.
- 7. 0.
0. 5.

GRUPA 2
Uwaga: każdy student wybiera dane zestawu o numerze odpowiadającym swojemu numerowi z listy
(patrz numeracja w załączonym pliku z obecnością na pierwszym laboratorium)
Nr przykładu
Macierz A
wartości własne
1
- 8. 6.
6. - 8.
- 14. 0.
0. - 2.
2
1. 5.
5. 1.
- 4. 0.
0. 6.
3
- 7. - 6.
- 6. - 7.
- 13. 0.
0. - 1.
4
7. 12.
12. 7.
- 5. 0.
0. 19.
5
- 7. - 11.
- 11. - 7.
- 18. 0.
0. 4.
6
- 4. 5.
5. - 4.
- 9. 0.
0. 1.
7
- 3. 12.
12. - 3.
- 15. 0.
0. 9.
8
6. 12.
12. 6.
- 6. 0.
0. 18.
9
11. 9.
9. 11.
2. 0.
0. 20.
10
1. 14.
14. 1.
- 13. 0.
0. 15.
11
- 1. 5.
5. - 1.
- 6. 0.
0. 4.
12
1. 15.
15. 1.
- 14. 0.
0. 16.
13
1. 11.
11. 1.
-10. 0.
0. 12.
14
- 4. 12.
12. - 4.
- 16. 0.
0. 8.
15
- 3. 9.
9. - 3.
- 12. 0.
0. 6.
16
9. 11.
11. 9.
- 2. 0.
0. 20.
17
5. 15.
15. 5.
- 10. 0.
0. 20.
18
- 5. - 15.
- 15. - 5.
- 20. 0.
0. 10.
19
- 2. 15.
15. - 2.
- 17. 0.
0. 13.
20
- 1. - 11.
- 11. - 1.
- 12. 0.
0. 10.
21
- 9. 3.
3. - 9.
22
5. 1.
1. 5.
23
7. 1.
1. 7.
24
8. 3.
3. 8.
25
7. 10.
10. 7.

GRUPA 3
Uwaga: każdy student wybiera dane zestawu o numerze odpowiadającym swojemu numerowi z listy
(patrz numeracja w załączonym pliku z obecnością na pierwszym laboratorium)
Nr przykładu
Macierz A
wartości własne
1
3. 2.
2. 3.
- 8. 0.
0. - 2.
2
2. 10.
10. 2.
2. 0.
0. 14.
3
2. 9.
9. 2.
- 3. 0.
0. 7.
4
8. 2.
2. 8.
1. 0.
0. 13.
5
9. 2.
2. 9.
- 4. 0.
0. 18.
6
5. 2.
2. 5.
- 19. 0.
0. 5.
7
5. 4.
4. 5.
- 13. 0.
0. 17.
8
- 7. 4.
4. - 7.
- 9. 0.
0. - 3.
9
15. 4.
4. 15.
3. 0.
0. 21.
10
3. 2.
2. 3.
- 1. 0.
0. 9.
11
3. 20.
20. 3.
2. 0.
0. 14.
12
- 2. 10.
1. 4.
- 8. 0.
0. 4.
13
10. 20.
20. 10.
- 18. 0.
0. - 6.
14
10. 1.
1. 10.
- 2. 0.
0. 4.
15
12. 1.
1. 12.
- 8. 0.
0. 4.
16
- 4. 1.
1. - 4.
- 12. 0.
0. - 6.
17
- 4. 8.
8. - 4.
- 4. 0.
0. 8.
18
3. 1.
1. 3.
- 15. 0.
0. 7.
19
7. 2.
2. 7.
- 8. 0.
0. 2.
20
7. 3.
3. 7.
- 7. 0.
0. 5.
21
- 9. 2.
2. - 9.
22
5. -2.
-2. 5.
23
7. -1.
-1. 7.
24
8. -3.
-3. 8.
25
-7. 10.
10. -7.

GRUPA AWANS
Uwaga: każdy student wybiera dane zestawu o numerze odpowiadającym swojemu numerowi z listy
(patrz numeracja w załączonym pliku z obecnością na pierwszym laboratorium)
Nr przykładu
Macierz A
wartości własne
1
- 4. 3.
3. - 4.
- 8. 0.
0. - 2.
2
- 9. 3.
3. - 9.
2. 0.
0. 14.
3
5. 1.
1. 5.
- 3. 0.
0. 7.
4
7. 1.
1. 7.
1. 0.
0. 13.
5
8. 3.
3. 8.
- 4. 0.
0. 18.
6
7. 10.
10. 7.
- 19. 0.
0. 5.
7
6. 4.
4. 6.
- 13. 0.
0. 17.
8
- 7. -3.
-3. - 7.
- 9. 0.
0. - 3.
Wyszukiwarka
Podobne podstrony:
MNM mgr 2014, przyklad obliczeniowy nr 3
MNM mgr 2014 przyklad obliczeniowy do lab 1
Budownictwo Ogólne 2 - Projekt - przykład 2, Pozycja obliczeniowa nr 4, Obliczenia ław fundamentowyc
Pozycja obliczeniowa nr 1, 11 - PWr WBLiW, Budownictwo Ogólne, Budownictwo Ogólne 2 - Projekt - przy
# Projekt nr 3 PRZYKŁAD obliczeniowy
Pozycja obliczeniowa nr 4, 11 - PWr WBLiW, Budownictwo Ogólne, Budownictwo Ogólne 2 - Projekt - przy
Przykładowe obliczenia
Przykład obliczeniowy, silniki spalinowe
Przykładowe obliczenia
Przykładowe obliczenia 6
7 zastosowane wzory i przykłady obliczeń KLE42RIDPUEF7SANZ7WMUANY3RP66KWCLYLQQBY
PRZYKŁAD OBLICZENIA ŚCIANY MUROWANEJ, BUDOWNICTWO, Konstrukcje Drewniane, Konstrukcje Drewniane, Bud
E Mazanek Przyklady obliczen z podstaw konstrukcji maszyn czesc 2
więcej podobnych podstron