ELEMENTY TEORII U ·

ZYTECZNO´SCI

Fenomen funkcji u·

zyteczno´sci wynika z faktu, ·

ze bardzo cz ¾

esto nie stosujemy zasady

multiplikatywno´sci rozwa·

zaj ¾

ac nasz maj ¾

atek. W pewnym sensie go "przedominowujemy". Dla

konkretnego przypadku de…niujemy funkcj ¾

e u·

zyteczno´sci u(w) : [0; 1) ! R. Maj ¾

ac okre´slon ¾

a

funkcj ¾

e u·

zyteczno´sci w celu rozwa·

zania ró·

znych sytuacji losowych mo·

zemy stosowa´c poj ¾

ecie

warto´sci oczekiwanej. Oczywistym jest, ·

ze funkcja u·

zyteczno´sci musi by´c niemalej ¾

aca.

Niech X, Y oznaczaj ¾

a dwa projekty ekonomiczne okre´slone przez zmienne losowe. Za÷

ó·

zmy,

·

ze mamy okre´slon ¾

a funkcj ¾

e u·

zyteczno´sci u(w). Zasada wyboru jest prosta:

X

lepsze ni·

z Y () E [u(X)] > E [u(Y )].

Powy·

zsze uporz ¾

adkowanie projektów ekonomicznych pozwala na rozwa·

zenie rodziny funkcji

u·

zyteczno´sci równowa·

znych funkcji u:

(u (w)

() u(w)) () u (W ) = a u(w) + b, a > 0.

Istotnie,

E[u (X)] > E[u (Y )]

() E[a u(X) + b] > E[a u(Y ) + b] () E[u(X)] > E[u(Y )].

Powy·

zsze rozwa·

zenie pozwala na taki dobór funkcji u·

zyteczno´sci, by np. u(0) =

1

oraz

u(w

max

) = 0

.

Przyk÷

ad

Za÷

ó·

zmy, ·

ze w

max

= 20000

. Przypu´scmy, ·

ze prawdopodobie´nstwo ca÷

kowitej straty maj ¾

atku

wynosi

1
2

. Zadajmy pytanie decydentowi (decision maker, owner) jak ¾

a maksymalnie sk÷

adk¾

e

b ¾

edzie sk÷

onny zap÷

aci´c, by ubezpieczy´c si ¾

e ca÷

kowicie od szkody. Niech G oznacza maksymaln ¾

a

sk÷

adk¾

e za ubezpieczenie si ¾

e od szkody. Wówczas

u(20000

G) =

1
2

u(0) +

1
2

u(20000)

.

Niech G = 12000. Wtedy u(20000

12000) =

1
2

+

1
2

0 =

1
2

, a zatem u(8000) =

1
2

.

Rozwi ¾

azuj ¾

ac powy·

zszy przyk÷

ad wypisali´smy równanie u·

zyteczno´sci dla decydenta.

W ogólnym przypadku równanie to wygl ¾

ada nast ¾

epuj ¾

aco: u(w

max

G) = E [u(w

max

X)]

.

Zauwa·

zmy, ·

ze w przypadku gdy u(w) =

w +

,

> 0

mamy

(w

G) +

= E [

(w

X) + ]

() G = E[X].

W praktyce ubezpieczeniowej G = (1 + ) E[X] + C. Zatem G > E[X].

Mówimy, ·

ze decydent jest risk-averse, je·

zeli jego funkcja u·

zyteczno´sci ma dwie w÷

asno´sci:

1. u

0

(w) > 0

2. u

00

(w) < 0

.

1

Poka·

zemy, ·

ze dla sytuacji, gdy decydent jest risk-averse i ubezpieczyciel jest risk-

averse istnieje mo·

zliwo´s´c zawarcia ubezpieczenia. Wpierw napiszemy równanie u·

zyteczno´sci

dla ubezpieczyciela (insurer).

Niech u

i

b ¾

edzie funkcj ¾

a u·

zyteczno´sci dla ubezpieczyciela,

w

i

maj ¾

atkiem ubezpieczyciela, za´s H sk÷

adk ¾

a jak ¾

a godzi si ¾

e przyj ¾

a´c ubezpieczyciel za ryzyko

X

. Wówczas u

i

(w

i

) = E [u

i

(w

i

X + H)]

. Poka·

zemy, ·

ze je·

zeli w÷

a´sciciel i ubezpieczyciel s ¾

a

risk-averse to jest mo·

zliwo´s´c do zawarcia ubezpieczenia. W dowodzie wykorzystamy znan ¾

a

z rachunku prawdopodobie´nstwa nierówno´s´c Jensena: E[u(X)]

u (E [X])

. Mamy

u(w

G) = E[u(w

X)]

u(w

E[X])

() w

G < w

E[X]

() G > E[X]

u

i

(w

i

) = E[u(w

i

X + H)]

u

i

(w

i

E[X] + H) =

) w

i

< w

i

E[X] + H

() H > E[X].

Przyk÷

ady

1. Rozwa·

zmy funkcj ¾

e u(w) =

e

w

,

> 0

. Zauwa·

zmy, ·

ze u

0

(w) =

e

w

> 0

oraz

u

00

(w) =

2

e

w

< 0

. Zatem funkcja ta opisuje decydenta typu risk-averse. Niech X > 0

b ¾

edzie strat ¾

a losow ¾

a. Wówczas

u(w

G) = E[u(w

X)]

e

(w G)

= E[ e

(w X)

]

e

G

= E[e

X

] = M

X

( )

G =

1

ln M

X

( )

.

Zatem sk÷

adka w tym przypadku nie zale·

zy od warto´sci maj ¾

atku w. Przy tej samej funkcji

u·

zyteczno´sci dla ubezpieczyciela mamy:

u

i

(w

i

) = E[u

i

(w

i

X + H)]

e

w

i

= E[ e

(w

i

X+H)

]

1 = E[e

H

e

X

] = e

H

E[e

X

]

e

H

= E[e

X

]

H =

1

ln M

X

( )

.

W tym przypadku sk÷

adka równie·

z nie zale·

zy od maj ¾

atku w.

2. Niech u(w) =

p

w

. Wówczas u

0

(w) =

1

2

p

w

> 0

oraz u

00

(w) =

1

4

p

w

3

< 0

. Zatem tak

zde…niowana funkcja u·

zyteczno´sci odpowiada równie·

z decydentowi typu risk-averse. Zauwa·

zmy

ponadto, ·

ze

u(w

G) = E[u(w

X)]

p

w

G = E[

p

w

X]

G = w

E[

p

w

X]

2

.

3. Za÷

ó·

zmy, ·

ze u(w) = ln w. Wtedy u

0

(w) =

1

w

> 0

oraz u

00

(w) =

1

w

2

< 0

. Zatem tak

okre´slona funkcja u·

zyteczno´sci okre´sla decydenta typu risk-averse. Ponadto

u(w

G) = E[u(w

X)]

ln(w

G) = E[ln(w

X)]

G = w

e

E[ln(w X)]

.

2

4. Rozwa·

zmy funkcj ¾

e u·

zyteczno´sci u(w) = w

w

2

. Zauwa·

zmy, ·

ze u

0

(w) = 1

2 w

oraz

u

00

(w) =

2

. Funkcja ta opisuje decydenta typu risk-averse je·

zeli

2 0;

1

2w

. Wówczas

u(w

G) = E[u(w

X)]

w

G

(w

G)

2

= E[w

X

(w

X)

2

]

G

2

+ (1

2 w) G = E[X] +

E[ 2wX + X

2

]

.

Ubezpieczenie optymalne

Za÷

ó·

zmy, ·

ze decydent ma funkcj ¾

e u·

zyteczno´sci u(w) i jest risk-averse. Niech posiada on

maj ¾

atek w, za´s X oznacza strat ¾

e losow ¾

a tego maj ¾

atku. Za÷

ó·

zmy, ·

ze decydent ma do wyboru

wszystkie dost ¾

epne na rynku typy polis w celu zabezpieczenia si ¾

e na wypadek straty. Jedn ¾

a

z polis jest I

d

(x) =

(

0

x

d

x

d x > d

. Jest to rodzaj polisy stop loss (excess of loss), tzn. polisy

która wyp÷

aca zawsze mniej, ni·

z wynosi szkoda.

Lemat

Funkcja g(d) =

1

R

d

(x

d) f (x)dx

, gdzie f jest g ¾

esto´sci ¾

a zmiennej losowej X (o ile EX

istnieje i jest sko´nczona), jest monotoniczna.

Dowód

Poka·

zemy, ·

ze

1

R

d

(x

d) f (x)dx =

1

R

d

[1

F (x)]dx

, gdzie F jest dystrybuant ¾

a zmiennej losowej

X

. Istotnie, ca÷

kuj ¾

ac przez cz ¾

e´sci mamy

1

R

d

(x

d) f (x)dx =

[(x

d) (1

F (x))]

1
d

+

1

R

d

[1

F (x)]dx

.

Do wykazania tezy wystarczy wykaza´c, ·

ze lim

x!1

[(x

d) (1

F (x))] = 0

, co jest równowa·

zne

temu, ·

ze lim

x!1

[x

(1

F (x)] = 0

.

Z za÷

o·

zenia wiadomo, ·

ze E[X] =

1

R

0

x

f (x)dx <

1.

Z odpowiedniego twierdzenia wiemy, ·

ze

1

R

0

g(x)dx <

1

()

1

R

G

g(x)dx

G!1

!

0

.

St ¾

ad

0

x [1

F (X)] = x

1

R

x

f (t)dt

1

R

x

t f (t)dt

x!1

! 0. Wobec tego lim

x!1

[x (1

F (x)] = 0

,

a wi ¾

ec ostatecznie funkcja g jest monotoniczna.

Wniosek

Z dowodu lematu wnioskujemy, ·

ze badanie monotoniczno´sci funkcji g sprowadza si ¾

e do

badania monotoniczno´sci funkcji

1

R

d

[1

F (x)]dx

. Ponadto g

0

(d) =

[1

F (d)] = F (d)

1 < 0

,

zatem funkcja g jest malej ¾

aca. Co wi ¾

ecej, g(0) = E[X] oraz lim

d!1

g(d) = 0

.

Zauwa·

zmy równie·

z, ·

ze równanie P =

1

R

d

(x

d) f (x)dx

posiada jednoznaczne rozwi ¾

azanie

dla 0 < P

E[X]

.

3

Twierdzenie (o optymalnym ubezpieczeniu)

Niech X b ¾

edzie zmienn ¾

a losow ¾

a straty decydenta. Je´sli

1. E[X] istnieje

2. decydent przeznacza na ubezpieczenie kwot ¾

e 0 < P

E[X]

3. na rynku dost ¾

epne s ¾

a wszystkie mo·

zliwe ubezpieczenia I(x) z uwag ¾

a, ·

ze I(X)

X

4. decydent jest risk-averse i ma funkcj ¾

e u·

zyteczno´sci u oraz maj ¾

atek w

5. ka·

zde ubezpieczenie kupowane jest za warto´s´c oczekiwan ¾

a wyp÷

aty E[I(X)]

to oczekiwana warto´s´c u·

zyteczno´sci decydenta osi ¾

aga maksimum przy zakupie ubezpieczenia

I

d

(x)

, gdzie d jest rozwi ¾

azaniem równania P =

1

R

d

(x

d) f (x)dx

.

Dowód

Zauwa·

zmy, ·

ze u(a)

u(b)

u

0

(b) (a

b)

dla dowolnych a; b 2 D

u

. Wobec tego otrzymujemy

u(w

x + I(w)

P )

u(w

x + I

d

(x)

P )

(I(x)

I

d

(x)) u

0

(w

x + I

d

(x)

P )

( )

[I(x)

I

d

(x)] u

0

(w

d

P )

.

Poka·

zemy teraz prawdziwo´s´c nierówno´sci ( ). Rozwa·

zmy trzy przypadki:

1. Je·

zeli I(x) = I

d

(x)

to w nierówno´sci ( ) zachodzi równo´s´c.

2. Je·

zeli I

d

(x) > I(x)

, to z faktu, ·

ze I

d

(x) > 0

mamy I

d

(x) = x

d

, co z kolei implikuje

nierówno´s´c x > d . Wówczas L = [I(x)

I

d

(x)] u

0

(w

d

P ) = P

.

3. Je·

zeli I

d

(x) < I(x)

, to I(x)

I

d

(x) > 0

. Zauwa·

zmy, ·

ze I

d

(x)

x

d

. Zatem

w

x + I

d

(x)

P > w

d

P

. Poniewa·

z u

00

< 0

, a wi ¾

ec funkcja u

0

jest malej ¾

aca wobec

ostatniej nierówno´sci wnioskujemy, ·

ze u

0

(w

x+I

d

(x)

P )

u

0

(w

d

P )

, zatem nierówno´s´c

( )

jest prawdziwa dla tego przypadku.

Wobec powy·

zszych rozwa·

za´n mamy, ·

ze

8

x

u(w

x + I(x)

P )

u(w

x + I

d

(x)

P )

[I(x)

I

d

(x)] u

0

(w

d

P )

.

Wstawiaj ¾

ac w powy·

zszej nierówno´sci X w miejsce x otrzymujemy

u(w

X + I(X)

P )

u(w

X + I

d

(X)

P )

[I(X)

I

d

(X)] u

0

(w

d

P )

gdzie X jest strat ¾

a losow ¾

a.

Przyk÷

adaj ¾

ac stronami w powy·

zszej nierówno´sci warto´s´c

oczekiwan ¾

a mamy

E [u(w

X + I(X)

P )]

E[u(w

X + I

d

(X)

P )]

E [I(X)

I

d

(X)] u

0

(w

d

P )

.

Z za÷

o·

ze´n twierdzenia wynika jednak, ·

ze E[I(X)]

E[I

d

(X)] = E[I(X)]

P = P

P = 0

.

Wobec tego

E[u(w

X + I(X)

P )]

E[u(w

X + I

d

(X)

P )]

.

Ostatnia nierówno´s´c dowodzi zapowiadanej tezy, poniewa·

z oczekiwana u·

zyteczno´s´c dla

dowolnej polisy z rozwa·

zanego zbioru jest niewi ¾

eksza ni·

z dla polisy stop loss.

4

Uwagi

1. Teza twierdzenia nie zale·

zy ani od funkcji u·

zyteczno´sci, ani od maj ¾

atku decydenta, co

jest korzy´sci ¾

a tego twierdzenia.

2. Ograniczeniem stosowalno´sci tego twierdzenia jest za÷

o·

zenie, ·

ze cena polisy jest równa

warto´sci oczekiwanej wyp÷

at.

3. Drugim ograniczeniem jest za÷

o·

zenie o z góry zadanej wysoko´sci sk÷

adki.

Przyk÷

ad

Niech u(w) =

e

w

, W oznacza maj ¾

atek decydenta, za´s X zmienn ¾

a losow ¾

a, która oznacza

brak straty z prawdopodobie´nstwem q, za´s zaj´scie straty z prawdopodobie´nstwem p. Je·

zeli

zasz÷

a strata, wówczas X ma g ¾

esto´s´c dan ¾

a wzorem f (x) = p

e

x

, x > 0. Wówczas mamy

u(w

G) = E[u(w

X)]

e

(w G)

= q u(w) +

1

R

0

u(w

x) p

e

x

dx

e

(w G)

=

q e

w

p

1

R

0

e

(w x)

e

x

dx

e

G

= q + p

1

R

0

e

(

) x

dx = q + p

1

G =

1

ln q +

p

.

Przyk÷

ad

Niech u(w) =

e

w

, W oznacza maj ¾

atek decydenta, za´s X zmienn ¾

a losow ¾

a, która oznacza

brak straty z prawdopodobie´nstwem q, za´s zaj´scie straty z prawdopodobie´nstwem p. Je·

zeli

zasz÷

a strata, wówczas X ma g ¾

esto´s´c dan ¾

a wzorem f (x) = p

e

x

, x > 0. Za÷

ó·

zmy, ·

ze

decydent nie chce ubezpieczy´c ca÷

ego ryzyka, tylko po÷

ow¾

e ryzyka, tzn. I(x) =

x
2

. Wówczas

E u w

x

2

G

= E[u(w

X)]

q u(w

G) + p

1

R

0

u w

x

2

G

e

x

dx = q u(w) + p

1

R

0

u (w

x) e

x

dx

q e

(w G)

+ p

1

R

0

e

(

w

x
2

G

) e

x

dx = q e

w

+ p

1

R

0

e

(w x)

e

x

dx

q e

G

+ p

1

R

0

e

(

x
2

G

) e

x

dx = q + p

1

R

0

e

(

) x

dx

q e

G

+ p

e

G

1

2

= q +

p

e

G

=

q+

p

q+

p

2

G =

1

ln

q+

p

q+

p

2

.

5

INDYWIDUALNA TEORIA RYZYKA

Niech X

1

; :::; X

n

b ¾

edzie ci ¾

agiem nieujemnych niezale·

znych zmiennych losowych, które

interpretujemy jako ´swiadczenia wyp÷

acone z i-tej polisy. Inaczej, zak÷¾

adamy, ·

ze w ustalonym

czasie mamy ustalony niezmienny portfel n polis. Taki portfel polis nazywamy zamkni ¾

etym.

Naszym celem b ¾

edzie badanie zmiennej losowej X = X

1

+ ::: + X

n

. W celu ustalenia sk÷

adki

za polis ¾

e nale·

zy z regu÷

y zbada´c S, które z natury rzeczy jest zmienn ¾

a losow ¾

a lub procesem.

Przyk÷

ad

P÷

acimy b z÷

otych w przypadku ´smierci, która nast ¾

epuje z prawdopodobie´nstwem q. Niech

X = I b

, gdzie I

0

1

p

q

. Zmienna losowa I nosi nazw¾

e indykatora. Rozumowanie mo·

zemy

rozszerzy´c w nast ¾

epuj ¾

acy sposób: niech X = I B, gdzie I jest indykatorem, który przyjmuje

warto´s´c 0, gdy z danej polisy nie by÷

o ·

zadnych wyp÷

at, za´s 1, gdy by÷

a cho´c jedna wyp÷

ata.

Zmienna losowa B przyjmuje warto´sci równe wyp÷

acie, gdy jakakolwiek szkoda mia÷

a miejsce.

Przyk÷

ad

Rozwa·

zmy ubezpieczenie na ·

zycie z dodatkow ¾

a wyp÷

at ¾

a, je·

zeli ´smier´c nast ¾

epuje w wyniku

nieszcz ¾

e´sliwego wypadku. Niech b b ¾

edzie wyp÷

at ¾

a za ´smier´c naturaln ¾

a, za´s 2b wyp÷

at ¾

a za ´smier´c

w nieszcz ¾

e´sliwym wypadku. Przyjmijmy, ·

ze P (B = b^I = 1) = p

1

, za´s P (B = 2b^I = 1) = p

2

,

przy czym p

2

< p

1

. Chcemy pozna´c rozk÷

ad zmiennej losowej X = I B.

P (X = 0) = P (X = 0

jI = 0) P (I = 0) + (X = 0jI = 1) P (I = 1) =

= P (X = 0

jI = 0) P (I = 0) + 0 = 1 P (I = 0) = P (I = 0)

P (I = 1) = P (I = 1

^ (B = b _ B = 2b)) = P (I = 1 ^ B = b) + P (I = 1 ^ B = 2b) = p

1

+ p

2

P (I = 0) = 1

P (I = 1) = 1

p

1

p

2

P (X = b) = P (X = b

jI = 1) P (I = 1) + P (X = bjI = 0) P (I = 0) =

= P (X = b

jI = 1) P (I = 1) = P (B = bjI = 1) P (I = 1) = p

1

P (X = 2b) = p

2

.

Zatem X

0

b

2b

1

p

1

p

2

p

1

p

2

.

Policzymy teraz E[X] oraz V ar[X].

Zak÷

adamy,

·

ze

=

E[B

jI

=

1]

, za´s

2

= V ar[B

jI = 1]. Przy obliczeniach podstawowym narz¾

edziem b ¾

ed ¾

a wzory znane z rachunku

prawdopodobie´nstwa.

Dla zmiennych losowych X, Y zachodz ¾

a E[X] = E [E [XjY ]] oraz

V ar[X] = E [V ar[X

jY ]] + V ar[E[XjY ]]. Zauwa·

zmy, ·

ze XjI = s

s

0

P (X

jI = s) p q

.

Wobec tego E[X] = E [E [XjI]] =

q = q

oraz V ar[EjI] = V ar[

I] =

2

V ar[I] =

2

pq

.

Ponadto V ar[XjI = 0] = 0, V ar[XjI = 1] = V ar[BjI = 1] =

2

oraz E[V ar[XjI]] =

2

q

.

Zatem V ar[X] =

2

q +

2

pq

. Z niezale·

zno´sci X

1

; :::; X

n

÷

atwo policzy´c E[S] oraz V ar[S].

6

Niech X, Y b ¾

ed ¾

a niezale·

znymi zmiennymi losowymi. Znajdziemy rozk÷

ad zmiennej losowej

S = X + Y

.

1. Niech X, Y b ¾

ed ¾

a ci ¾

ag÷

ymi zmiennymi losowymi. Wówczas

F

S

(s) = P (X + Y

s) =

1

R

0

P (X + Y

s

jY = y) f

Y

(y)dy =

=

s

R

0

P (X + Y

s

jY = y) f

Y

(y)dy =

s

R

0

P (X

s

y) f

Y

(y)dy =

=

s

R

0

F

X

(s

y) f

Y

(y)dy = (F

X

F

Y

)(s)

.

2.

Niech X

x

1

x

2

:::

x

n

:::

p

1

p

2

:::

p

n

:::

, Y

y

1

y

2

:::

y

n

:::

p

2

1

p

2

2

:::

p

2

n

:::

b ¾

ed ¾

a dyskretnymi

zmiennymi losowymi. Wówczas

P (X + Y = x

l

+ y

k

) =

1

P

k=1

P (X + Y = x

l

+ y

k

jY = y

k

) P (Y = y

k

) =

=

P

y

k

P (X = x

l

) P (Y = y

k

) = P

X

P

Y

.

Ogólnie F

S

(s) =

P

y

k

s

F

X

(s

y

k

) P (Y = y

k

)

.

Przyk÷

ad

Niech X

U ((0; 2))

, Y

U ((0; 3))

. Znadziemy dystrybuant ¾

e zmiennej losowej S = X + Y .

Wiadomo, ·

ze F

X

(s) =

8

>

>

<

>

>

:

0

s < 0

s
2

s

2 [0; 2)

1

s > 2

, f

Y

(y) =

(

1
3

y

2 (0; 3)

0 y =

2 (0; 3)

. Rozwa·

zmy przypadki:

1. s

0

. Wtedy F

S

(s) = 0

2. 0 < s < 2. Wówczas

F

S

(s) =

1
3

s

R

0

F

X

(s

y)dy =

1
3

s

R

0

1
2

(s

y)dy =

1

12

(s

y)

2 y=s

y=0

=

1

12

s

2

.

3. 2 < s

3

. Zauwa·

zmy, ·

ze je·

zeli s

y > 2

, to y 2 (0; 2). Zatem

F

S

(s) =

1
3

s

R

0

F

X

(s

y)dy =

1
3

s 2

R

0

1dy +

s

R

s 2

1
2

(s

y)dy =

1
3

(s

2)

1

12

(s

y)

2 y=s

y=s 2

=

=

1
3

(s

1)

.

4. 3 < s

5

. Wówczas je´sli s

y > 2

, to y < s

2

. St ¾

ad

F

S

(s) =

1
3

3

R

0

F

X

(s

y)dy =

1
3

s 2

R

0

1dy +

3

R

s 2

1
2

(s

y)dy

=

=

1
3

h

s

2

1
4

(s

y)

2 y=3

y=s 2

i

=

1
3

(s

1

1
4

s

2

+

3
2

s

9
4

) =

1
3

1
4

s

2

+

5
2

s

13

4

.

5. s > 5. Wtedy F

S

(s) = 1

.

Ostatecznie F

S

(s) =

8

>

>

>

>

>

>

>

<

>

>

>

>

>

>

>

:

0

s

0

1

12

s

2

s

2 (0; 2]

1
3

(s

1)

2 < s

3

1
3

1
4

s

2

+

5
2

s

1

13

3 < s

5

1

s > 5

.

7

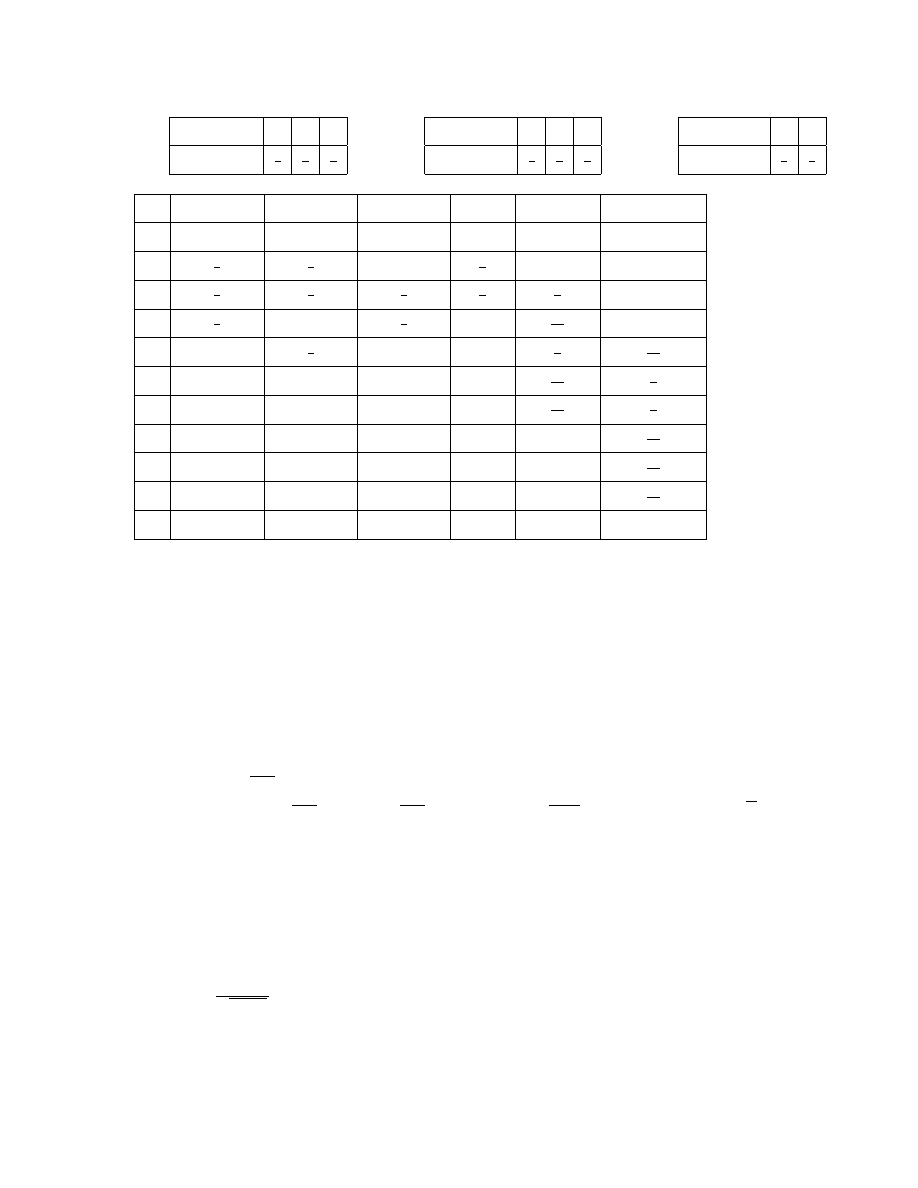
Przyk÷

ad

Niech

dane

b ¾

ed ¾

a

zmienne

losowe

X

,

Y

,

Z

o

rozk÷

adach

dyskretnych:

X

x

1

2

3

P (X = x)

1
3

1
3

1
3

, Y

x

1

2

4

P (Y = x)

1
2

1
4

1
4

, Z

x

2

3

P (Z = x)

1
3

2
3

.

Znajdziemy rozk÷

ad zmiennej losowe X + Y + Z.

x

P (X = x)

P (Y = x)

P (Z = x)

F

X

(x)

F

X+Y

(x)

F

X+Y +X

(x)

0

0

0

0

0

0

0

1

1
3

1
2

0

1
3

0

0

2

1
3

1
4

1
3

2
3

1
6

0

3

1
3

0

2
3

1

5

12

0

4

0

1
4

0

1

2
3

1

18

5

0

0

0

1

10
12

1
4

6

0

0

0

1

11
12

1
2

7

0

0

0

1

1

13
18

8

0

0

0

1

1

31
36

9

0

0

0

1

1

17
18

10

0

0

0

1

1

1

.

Metoda splotów, pozwala na znalezienie sumy dowolnej ilo´sc zmiennych losowych jest do´s´c

·

zmudna. W niektórych wypadkach warto stosowa´c funkcj ¾

e generuj ¾

ac ¾

a momenty do wyznaczenia

rozk÷

adu sumy niezale·

znych zmiennych losowych.

Niech X

1

; :::; X

n

b ¾

ed ¾

a niezale·

znymi

zmiennymi losowymi o funkcji generuj ¾

acej momenty M

X

k

(s)

. Niech S = X

1

+:::+X

n

. Wówczas

M

S

(s) = E e

s (X

1

+:::+X

n

)

nzl

= E[e

sX

1

] ::: E e

sX

n

= M

X

1

(s) ::: M

X

n

(s)

.

Przyk÷

ad

Niech X

k

N (

k

;

2

)

, k = 1; 2; :::; n b ¾

ed ¾

a niezale·

znymi zmiennymi losowymi. Wiadomo,

·

ze M

X

k

(s) = e

k

s+

2s2

2

. Wówczas

M

X

1

+:::X

n

(s) = e

1

s+

2s2

2

::: e

k

s+

2s2

2

= e

s (

1

+:::+

k

)+

n 2s2

2

N (

1

+ ::: +

n

;

p

n

2

)

.

Inny spsób wyznaczania rozk÷

adu sumy niezale·

znych zmiennych losowych jest aproksymacja

rozk÷

adem normalnym. Podstawowym twierdzeniem wykorzystywanym w tym sposobie jest

twierdzenie Linderberga-Levy’ego:

Niech X

1

; :::; X

n

b ¾

edzie ci ¾

agiem wzajemnie niezale·

znych zmiennych losowych o sko´nczonej

warto´sci oczekiwanej i wariancji. Rozwa·

zmy zmienn ¾

a losow ¾

a S = X

1

+ ::: + X

n

, n = 1; 2; :::.

Wóczas Y

n

=

S

n

EX

n

p

V arS

n

F

! N(0; 1). Dla n

30 Y

n

N (0; 1)

.

8

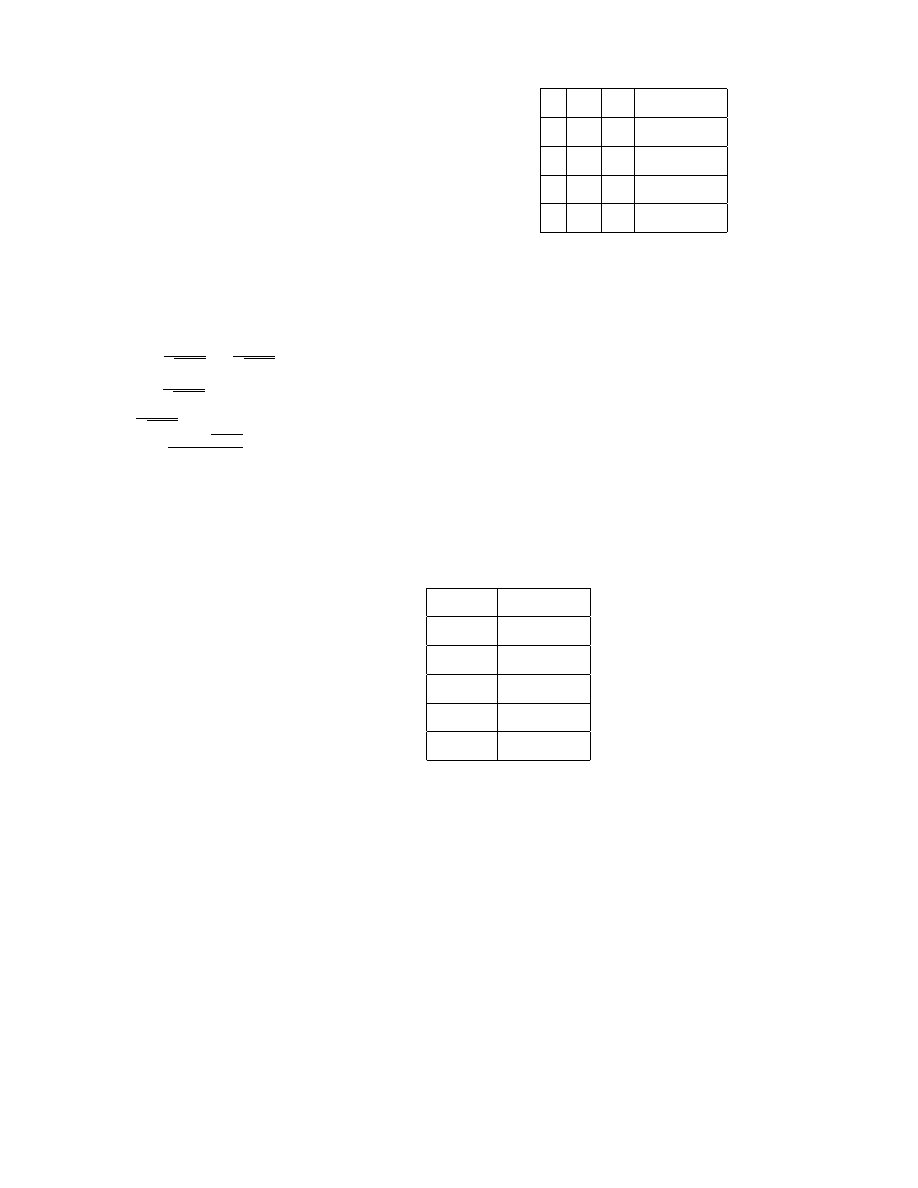
Przyk÷

ad

Ubezpieczyciel ma nast ¾

epuj ¾

acy portfel polis:

q

k

b

k

ilo´s´c polis

1

a

1

b

1

n

1

2

a

2

b

1

n

2

3

a

1

b

2

n

3

4

a

2

b

2

n

4

przy czym

n

1

+ n

2

+ n

3

+ n

4

> 100

. Ubezpieczyciel planuje zebra´c sk÷

adk¾

e wed÷

ug wzoru P = (1 + ) EX,

gdzie S jest sum ¾

a polis, za´s

wzgl ¾

ednym wspó÷

czynnikiem bezpiecze´nstwa.

Dla jakiego

zebrana sk÷

adka b ¾

edzie s prawdopodobie´nstwem 0; 95 wi ¾

eksza ni·

z wyp÷

acone ´swiadczenie?

P (S < (1 + ) ES) = 0; 95

P

S ES

p

V arS

EX

p

V arS

= 0; 95

ES

p

V arS

= 0; 95

ES

p

V arS

= 1; 645

=

1;645

p

V arS

ES

przy czym ES = n

1

a

1

b

1

+ n

2

a

2

b

1

+ n

3

a

1

b

2

+ n

4

a

2

b

2

oraz

V arS = n

1

b

2

1

a

1

(1

a

1

) + n

2

b

2

1

a

2

(1

a

2

) + n

3

b

2

2

a

1

(1

a

1

) + n

4

b

2

2

a

2

(1

a

2

)

.

Przyk÷

ad

Towarzystwo ubezpiecze´n na ·

zycie posiada 16000 polis jednorocznego ubezpieczenia na ·

zycie

o nast ¾

epuj ¾

acych sumach ubezpieczenia:

b

k

ilo´s´c polis

10000

8000

20000

3500

30000

2500

50000

1500

100000

500

. Prawdopodobie´nstwo szkody

q

k

dla ka·

zdej z 16000 polis wynosi 0; 02. Zak÷

adamy, ·

ze ·

zycia s ¾

a niezale·

zne. Towarzystwo

ustanawia limit retencyjny (zatrzymania). Polega on na tym, ·

ze dla ka·

zdej polisy limit retencji

poni·

zej której towarzystwo "zatrzymuje" odpowiedzialno´s´c, a nadwy·

zka jest sprzedawana

reasekurantowi, np. je·

zeli limit retencji wynosi 20000 to towarzystwo zatrzymuje do 20000

w÷¾

acznie na ka·

zdej polisie i sprzedaje nadwy·

zk¾

e powy·

zej 20000.

Jako kryterium decyzji

towarzystwo chce zminimalizowa´c prawdopodobie´nstwo, ·

ze "zatrzymane" szkody powi ¾

ekszone

o koszty reasekuracji przekrocz ¾

a 8250000.

Cena reasekuracji wynosi 0,025 za z÷

otówk¾

e

przekazanej sumy. Za÷

ó·

zmy, ·

ze mamy do czynienia z zamkni ¾

etym uk÷

adem polis.

9

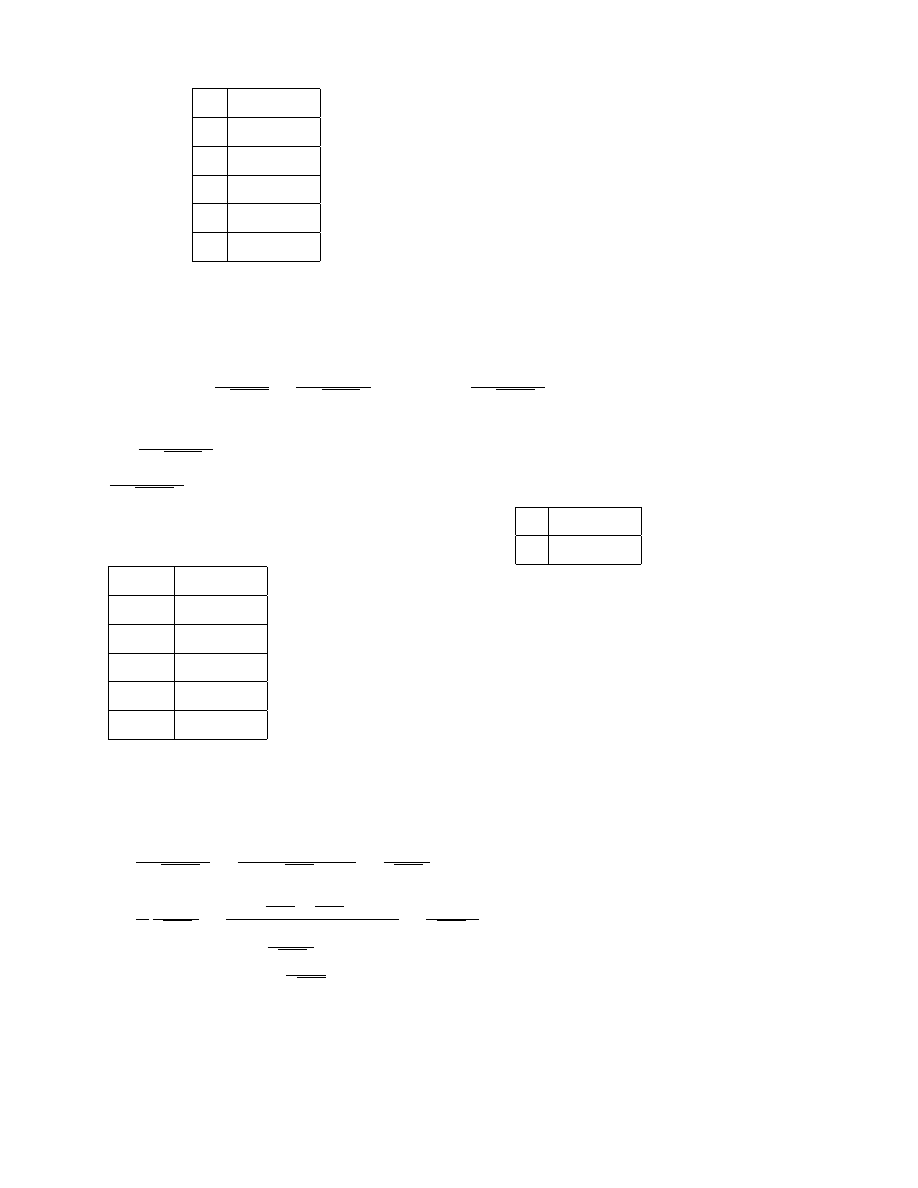
W celu uproszczenia rachunków dokonajmy nast ¾

epuj ¾

acej denominacji: niech portfel polis

ma posta´c

b

k

ilo´s´c polis

1

8000

2

3500

3

2500

5

1500

10

500

, za´s warto´s´c graniczna wynosi 825. Niech d b ¾

edzie kwot ¾

a retencji.

Oznaczmy poprzez S zmienn ¾

a losow ¾

a opisuj ¾

ac ¾

a portfel cedenta, za´s przez E kwot ¾

e, jak ¾

a cedent

musi zap÷

aci´c reasekuratorowi za przekazanie ryzyka. Zadanie polega na zminimalizowaniu

P (S + E > 825)

. Zauwa·

zmy, ·

ze

P (S + E > 825) = 1

P (S + E

825) = 1

P (S

825

E) =

= 1

P

S E[S]

p

V ar[S]

825 E E[S]

p

V ar[S]

1

825 E E[S]

p

V ar[S]

.

Aby

zminimalizowa´c

rozwa·

zane

prawdopodobie´nstwo

potrzeba

zmaksymalizowa´c

825 E E[S]

p

V ar[S]

, co z monotoniczno´sci dystrybuanty równowa·

zne jest zmaksymalizowaniu

825 E E[S]

p

V ar[S]

. Rozwa·

zmy nast ¾

epuj ¾

ace przypadki:

1. d 2 [0; 1]. Wówczas portfel cedenta ma posta´c

b

k

ilo´s´c polis

d

16000

za´s portfel reasekuranta

b

k

ilo´s´c polis

1

d

8000

2

d

3500

3

d

2500

5

d

1500

10

d

500

. Zatem

E = 0; 025 [(1

d) 8000 + (2

d) 3500 + (3

d) 2500 + (5

d) 1500 + (10

d) 500] =

= 875

400d

E[S] = 16000 d 0; 02 = 320d

V ar[S] = d

2

16000 0; 02 0; 98 = 313; 6d

2

825 E E[S]

p

V ar[S]

=

825 875+400d 320d

p

313;6d

=

80d 50

p

313;6d

.

Zauwa·

zmy, ·

ze

d

dd

80d 50

p

313;6d

=

80d

2

p

313;6

p

313;6 (80d 50)

313;6d

2

=

50

p

313;6d

2

zatem wyra·

zenie

80d 50

p

313;6d

jest rosn ¾

ace dla d 2 [0; 1]. Zatem najwi¾

eksz ¾

a warto´s´c przyjmuje dla

d = 1

. Jest ona równa

80 50

p

313;6

1; 694

.

10

2.

d

2 (1; 2].

Porfel cedenta ma posta´c

b

k

ilo´s´c polis

1

8000

d

8000

, za´s portfel reasekuranta

b

k

ilo´s´c polis

2

d

3500

3

d

2500

5

d

1500

10

d

500

. Mamy

E = 0; 025 (3500 (2

d) + 2500 (3

d) + 1500 (5

d) + 500 (10

d)) = 675

200d

E[S] = 0; 02 (8000 + 8000d) = 160 + 160d

V ar[S] = 0; 02 0; 98 (8000 + d

2

) = 156; 8 + 156; 8d

2

825 E E[S]

p

V ar[S]

=

825 675+200d 160 160d

p

156;8 (1+d

2

)

=

40d 10

p

156;8 (1+d

2

)

.

Zauwa·

zmy, ·

ze

d

dd

40d 10

p

156:8 (1+d

2

)

=

40 156;8 (1+d

2

) 6272d

2

+1568d

(

p

156: 8d

2

+156: 8

)

2

=

6272+1568d

p

156:8 (1+d

2

)

3

zatem wyra·

zenie

40d 10

p

156;8 (1+d

2

)

jest rosn ¾

ace dla d 2 (1; 2]. Dla d = 2 warto´s´c wyra·

zenia

wynosi

70

p

156;8 5

= 2; 5

.

3.

d

2 (2; 3].

Portfel cedenta ma posta´c

b

k

ilo´s´c polis

1

8000

2

3500

d

4500

za´s portfel reasekuranta

b

k

ilo´s´c polis

3

d

2500

5

d

1500

10

d

500

. St ¾

ad

E = 0; 025 (2500 (3

d) + 1500 (5

d) + 500 (10

d)) = 500

112; 5d

E[S] = 0; 02 (8000 + 2 3500 + d 4500) = 300 + 90d

V ar[S] = 0; 02 0; 98 (8000 + 4 3500 + d

2

2500) = 431; 2 + 88; 2d

2

825 E E[S]

p

V ar[S]

=

825 500+112;5d 300 90d

p

431;2+88;2d

2

=

25+22;5d

p

431;2+88;2d

2

.

Ponadto

d

dd

25+22;5d

p

431;2+88;2d

2

=

22: 5

(

431;2+88;2d

2

)

1984;5d

2

2205d

p

88;2d

2

+431; 2

3

=

9702 2205d

p

88;2d

2

+431;2

3

zatem dla d 2 (2; 3] wyra·

zenie

25+22;5d

p

431;2+88;2d

2

jest rosn ¾

ace. Ponadto dla d = 3 przyjmuje ono

warto´s´c 2; 6429.

11

4.

d

2 (3; 5].

Portfel cedenta ma posta´c

b

k

ilo´s´c polis

1

8000

2

3500

3

2500

d

2000

za´s portfel reasekuranta

b

k

ilo´s´c polis

5

d

1500

10

d

500

. Zatem

E = 0; 025 (1500 (5

d) + 500 (1

d)) = 312; 5

50d

E[S] = 0; 02 (8000 + 2 3500 + 3 2500 + d 2000) = 450 + 40d

V ar[S] = 0; 02 0; 98 (8000 + 4 3500 + 9 2500 + d

2

2000) = 872; 2 + 39; 2d

2

825 E E[S]

p

V ar[S]

=

825 312;5+50d 450 40d

p

872;2+39;2d

2

=

62;5+10d

p

872;2+39;2d

2

.

Ponadto

d

dd

62:5+10d

p

872:2+39:2d

2

=

10

(

872;2+39;2d

2

)

392d

2

2450d

p

39;2d

2

+872; 2

3

=

8720 2450d

p

39;2d

2

+872;2

3

zatem wyra·

zenie

62;5+10d

p

872;2+39;2d

2

osi ¾

aga maksimum dla d =

8720
2450

=

872
245

2 (3; 5] i jego warto´s´c

wynosi

9613

98

p

37

2; 6513

.

5. d 2 (5; 10]. Wówczas portfel cedenta ma posta´c

b

k

ilo´s´c polis

1

8000

2

3500

3

2500

5

1500

d

500

za´s portfel reasekuranta

b

k

ilo´s´c polis

10

d

500

. Wówczas

E = 0; 025 (500 (10

d)) = 125

12; 5d

E[S] = (8000 + 2 3500 + 3 2500 + 5 1500 + d 500) = 600 + 10d

V ar[S] = 0; 02 0; 98 (8000 + 4 3500 + 9 2500 + 25 1500 + d

2

500) = 1607; 2 + 9; 8d

2

825 E E[S]

p

V ar[S]

=

825 125+12;5d 600 10d

p

1607;2+9;8d

2

=

100+2;5d

p

1607;2+9;8d

2

.

Zauwa·

zmy, ·

ze

d

dd

100+2;5d

p

1607;2+9;8d

2

=

2; 5

(

1607;2+9;8d

2

)

24;5d

2

980d

p

9; 8d

2

+1607; 2

3

=

4018 980d

p

9;8d

2

+1607;2

3

czyli wyra·

zenie

100+2;5d

p

1607;2+9;8d

2

jest malej ¾

ace dla d 2 (5; 10]. Jego warto´s´c w punkcie d = 5

wynosi 2; 614.

Z powy·

zszych rozwa·

za´n otrzymujemy, ·

ze wyra·

zenie

825 E E[S]

p

V ar[S]

przyjmuje warto´s´c najwi ¾

eksz ¾

a

2; 6513

dla d =

872
245

. Ponadto

(2; 6513) = 0; 99599

. Zatem P (S + E > 825) b ¾

edzie minimalne,

je·

zeli limit retencji wynosi÷b ¾

edzie

872
245

3; 56

i równe wynosi´c b ¾

edzie 1

0; 99599 = 0; 00401

.

12

KOLEKTYWNA TEORIA RYZYKA

Niech X

1

; :::; X

n

b ¾

edzie ci ¾

agiem i.i.d. zmiennych losowych oraz X

k

0

, k = 1; :::; n. Niech N

b ¾

edzie zmienn ¾

a losow ¾

a przyjmuj ¾

ac ¾

a warto´sci ca÷

kowite nieujemne. Za÷

ó·

zmy, ·

ze zmienne losowe

N; X

1

; :::; X

N

s ¾

a wzajemnie niezale·

zne. Rozwa·

za´c b ¾

edziemy zmienn ¾

a losow ¾

a S = X

1

+ ::: + X

N

.

Zmienn ¾

a losow ¾

a S zde…niowan ¾

a w powy·

zszy sposób nazywamy zmienn ¾

a o rozk÷

adzie z÷

o·

zonym

(compund distribution). Mo·

zna j ¾

a interpretowa´c jako sum ¾

e wyp÷

at z danego portfela polis

w okre´slonym czasie.

Niech P (x) oznacza dystrybuant ¾

e zmiennej losowej X

k

= X

, za´s

p

k

= E X

k

. Znajdziemy dystrybuant ¾

e zmiennej losowej S:

P (S

s) =

1

P

n=0

P (S

s

jN = n) P (N = n) =

1

P

n=0

P (X

1

+ ::: + X

n

s) P (N = n) =

=

1

P

n=0

p

(n)

(s) P (N = n)

.

Przyk÷

ad

Niech X

1

2

3

1
3

1
3

1
3

za´s N

0

1

2

0; 2

0; 3

0; 5

.

Przyjmujemy, ·

ze p

(0)

(s)

0

1

.

Wówczas

P (S = s) =

1

P

n=0

p

(n)

(s) P (N = n) =

= p

(0)

(s) P (N = 0) + p

(1)

(s) P (N = 1) + p

(2)

(s) P (N = 2)

.

s

p(s)

p

(0)

(s)

p

(2)

(s)

P (S = s)

0

0

1

0

0; 2

1

1
3

0

0

0; 1

2

1
3

0

1
9

7

45

3

1
3

0

2
9

19
90

4

0

0

3
9

1
6

5

0

0

2
9

1
9

6

0

0

1
9

1

18

Je·

zeli X ma rozk÷

ad dyskretny, to S ma równie·

z rozk÷

ad dyskretny. Je·

zeli natomiast X ma

rozk÷

ad ci ¾

ag÷

y, to S nie musi mie´c rozk÷

adu ci ¾

ag÷

ego.

Inn ¾

a metod ¾

a wyznaczania rozk÷

adu zmiennej losowej S jest metoda funkcji generuj ¾

acej

momenty. Wyznaczymy funkcj ¾

e generuj ¾

ac ¾

a momenty zmiennej losowej S.

E e

tS

=

1

P

n=0

E e

tS

jN = n

P (N = n) =

1

P

n=0

E e

t (X

1

+:::+X

n

)

P (N = n) =

=

1

P

n=0

E e

tX

n

P (N = n) =

1

P

n=0

[M

X

(t)]

N

P (N = n) =

1

P

n=0

e

ln M

X

(t) n

P (N = n) =

= M

N

(ln M

X

(t))

.

Zatem M

S

(t) = M

N

[ln M

X

(t)]

.

13

Uwaga

Poka·

zemy, ·

ze je·

zeli rozk÷

ad jest kombinacj ¾

a liniow ¾

a dwóch innych rozk÷

adów, tzn.

F (x) =

F

1

(s) + (1

) F

2

(x)

, to M

F

(T ) =

M

F

1

(t) + (1

) M

F

2

(t)

.

M

F

(t) = E e

tX

=

1

R

1

e

tx

dF (x) =

1

R

1

e

tx

d [

F

1

(x) + (1

) F

2

(x)] =

=

1

R

1

e

tx

dF

1

(x) + (1

)

1

R

1

e

tx

dF

2

(x)

.

Z wzajemnej jednoznaczno´sci rozk÷

adu i funkcji generuj ¾

acej momenty wynika, ·

ze inaczej by´c

nie mo·

ze.

Przyk÷

ad

Niech zmienna losowa N ma rozk÷

ad geometryczny, za´s zmienna losowa X rozk÷

ad

wyk÷

adniczy. Wówczas P (x) = 1

e

x

, x > 0. W tym przypadku

M

S

(t) =

p

1 q M

X

(t)

=

p [1 qM

X

(t)+qM

X

(t)]

1 qM

X

(t)

= p + q

pM

X

(t)

1 qM

X

(t)

.

Zatem

M

S

(t) = p + q

p

1

t

1

q

1

t

= p + q

p

p t

.

Zauwa·

zmy przy tym, ·

ze 1 = M

0
1

(t)

. Z wcze´sniejszej uwagi wynika, ·

ze

S

p

0
1

+ q (1

e

px

)

.

Zatem F

S

(x) = p+q (1

e

px

) = 1

qe

px

. St ¾

ad wniosek, ·

ze S ma rozk÷

ad typu mieszanego

ze skokiem s = p w punkcie 0. Ponadto

E [S] = E [E [S

jN]] = p

1

E [N ]

E[S

jN] = n E [X] = p

1

n

V ar[S] = E [V ar[S

jN]] + V ar [E [SjN]] = E [n V ar[X]] + p

2

1

V ar[N ] =

= (p

2

p

2

1

) E[N ] + p

2

1

V ar[N ] = (p

2

p

2

1

) E [N ] + p

2

1

V ar[N ]

.

Przyk÷

ad

Je´sli N

P ( )

to M

S

(t) = M

N

(ln M

X

(t)) = e (

e

ln MX (t)

1

) = e

(M

X

(t) 1)

.

Ponadto

E[S] = p

1

E[N ] = p

1

oraz V ar[S] = (p

2

p

2

1

) + p

2

1

= p

2

.

Przyk÷

ad

Niech zmienna losowa N ma rozk÷

ad dwumianowy ujemny. Wówczas M

N

(t) =

p

1 qe

t

r

.

Zatem M

S

(t) =

h

p

1 qM

X

(t)

i

r

. Wiadomo, ·

ze E[N ] =

rq

p

za´s V ar[N ] =

rq
p

2

. Zatem

E[S] = p E[N ] = p

1

rq

p

V ar[S] = (p

2

p

2

1

)

rq

p

+ p

2

1

rq
p

2

=

rq

p

p

2

+ p

2

1

rq

p

1 +

1
p

=

rq

p

p

2

+

p

2

1

rq

p

q
p

=

rq

p

p

2

+

rq

2

p

2

1

p

2

.

14

Przyk÷

ad

Za÷

ó·

zmy, ·

ze dana jest rodzina zmiennych losowych o rozk÷

adzie Poissona taka, ·

ze

N

j

=

P ( )

.

Niech

b ¾

edzie zmienn ¾

a losow ¾

a ci ¾

ag÷¾

a o g ¾

esto´sci u( ).

Wyznacz

bezwarunkowy rozk÷

ad zmiennej losowej N .

P (N = n) =

1

R

0

P (N = n

j = ) u( )d =

1

R

0

e

n

n!

u( )d

.

Za÷

ó·

zmy, ·

ze u( )

( ; )

. Wówczas

P (N = n) =

1

R

0

e

n

n!

( )

e

1

d =

( ) n!

1

R

0

+n 1

e

( +1)

d =

=

( ) n!

( +1)

+n

( +1)

( +n)

( +1)

+n

1

R

0

+n 1

e

( +1)

d =

( +1)

n+

( +n)

( ) n!

.

Przyk÷

ad

Niech X

1

; :::; X

n

b ¾

ed ¾

a niezale·

znymi zmiennymi losowymi o rozk÷

adzie

( ; )

, czyli

f (x) =

( )

x

1

e

x

. Wówczas M

X

(s) =

s

. Korzystaj ¾

ac z niezale·

zno´sci zmiennych

losowych X

1

; :::; X

n

oraz z w÷

asno´sci funkcji generuj ¾

acej momenty mamy, ·

ze

M

X

1

+:::+X

n

(s) =

s

n

(n ; )

Przyk÷

ad

Niech N

P ( )

oraz X

1

; :::; X

N

b ¾

ed ¾

a niezale·

znymi zmiennymi losowymi o rozk÷

adzie

(1; 1) = Exp(1)

. Na mocy poprzedniego przyk÷

adu otrzymujemy, ·

ze

X

1

+ ::: + X

n

(n; 1)

1

(n)

e

x

x

n 1

dla x > 0. Znajdziemy teraz dystrybuant ¾

e zmiennej

losowej X

1

+ :::X

N

. Dla ustalenia uwagi przyjmijmy, ·

ze s > 0. Mamy

1

F

X

1

+:::+X

N

(s) = 1

F

(n)

(s) = 1

1

P

n=0

P (N = n) F

(n)

(s) =

=

1

P

n=0

P (N = n)

1

F

(n)

(s) =

1

P

n=1

P (N = n)

1

R

s

1

(n 1)!

e

x

x

n 1

dx =

=

1

P

n=1

1

R

s

1

(n 1)!

e

x

x

n 1

dx

n

e

n!

.

Zauwa·

zmy, ·

ze

g(n) =

1

(n 1)!

s

R

0

e

x

x

n 1

dx =

1

(n 1)!

[ e

x

x

n 1

]

1
s

+ (n

1)

1

R

s

e

x

x

n 2

dx =

=

e

s

s

n

1

(n 1)!

+

1

(n 2)!

1

R

s

e

x

x

n 2

dx

.

Zatem g(n) =

e

s

s

n

1

(n 1)!

+ g(n

1)

. St ¾

ad

g(n) =

e

s

s

n

1

(n 1)!

+

h

e

s

s

n

2

(n 2)!

+ g(n

2)

i

= ::: =

e

s

s

n

1

(n 1)!

+

e

s

s

n

2

(n 2)!

+ ::: +

e

s

s

1!

+ e

s

=

n 1

P

k=0

e

s

s

k

k!

.

Zatem

1

F

X

1

+:::+X

N

(s) =

1

P

n=1

1

R

s

1

(n 1)!

e

x

x

n 1

dx

n

e

n!

=

1

P

n=1

n

e

n!

n 1

P

k=1

s

k

e

s

k!

,

a wi ¾

ec ostatecznie

F

S

(s) = 1

1

P

n=1

n

e

n!

n 1

P

k=1

s

k

e

s

k!

.

15

Uwaga

Poniewa·

z w teoretycznie prostym przypadku dla rozk÷

adu wyk÷

adniczego dystrybuanta

rozk÷

adu z÷

o·

zonego jest skomplikowana nale·

zy zastanowi´c si ¾

e nad aproksymacj ¾

a. Przypu´s´cmy,

·

ze X daje si ¾

e przybli·

zy´c rozk÷

adem dyskretnym o sko´nczonej ilo´sci warto´sci.

Twierdzenie

Je·

zeli S

1

; :::; S

m

s ¾

a zmiennymi losowymi niezale·

znymi o z÷

o·

zonych rozk÷

adach Poissona

z parametrami (

i

; p

i

)

, i = 1; :::; m (gdzie p

i

jest dystrybuant ¾

a X

i

), to zmienna losowa

S = S

1

+ ::: + S

m

ma z÷

o·

zony rozk÷

ad Poissona o parametrach

=

m

P

i=1

i

; p =

m

P

i=1

i

p

i

.

Dowód

M

S

(t) = M

S

1

(t) ::: M

S

m

(t) = e

1

[

M

X1

(t) 1

] ::: e

m

[M

Xm

(t) 1]

= e

m

P

i=1

i

M

Xi

(t)

m

P

i=1

i

=

= e

m

P

i=1

i

m

P

i=1

i

M

Xi

(t) 1

.

Korzystaj ¾

ac z jednoznaczno´sci funkcji generuj ¾

acej momenty i z faktu, ·

ze kombinacja

funkcji generuj ¾

acej momenty odpowiada kombinacji liniowej dystrybuant otrzymujemy tez ¾

e

twierdzenia.

Przyk÷

ad

Niech x

1

; :::; x

m

b ¾

edzie dowolnym uk÷

adem liczb rzeczywistych oraz N

1

; :::; N

m

b ¾

edzie

ci ¾

agiem niezale·

znych zmiennych losowych o rozk÷

adzie Poissona z parametrami

1

; :::;

m

.

Ustalimy jaki jest rozk÷

ad S = x

1

N

1

+ ::: + x

m

N

m

.

Zauwa·

zmy, ·

ze x

i

N

i

mo·

zna traktowa´c jako zmienn ¾

a losow ¾

a o z÷

o·

zonym rozk÷

adzie Poissona

gdzie P (X = x

i

) = 1

. Po krótkim namy´sle stwierdzamy, ·

ze ka·

zd ¾

a ze zmiennych x

i

N

i

ma

z÷

o·

zony rozk÷¾

ad Poissona z parametrami

i

oraz P (X = x

i

) = 1

. Mo·

zemy zatem zastosowa´c

udowodnione twierdzenie. Wynika z niego, ·

ze S ma z÷

o·

zony rozk÷

ad Poissona z parametrami

=

n

P

i=1

i

; p =

m

P

i=1

i

p

i

.

De…nicja

Niech dany b ¾

edzie wektor losowy X = [X

1

; :::; X

m

]

. Wówczas

M

[X

1

;:::;X

n

]

(t

1

; :::; t

m

) = E

"

e

m

P

i=1

t

i

X

i

#

.

Twierdzenie

Zmienne losowe X

1

; :::; X

m

s ¾

a niezale·

zne wtedy i tylko wtedy, gdy

M

[X

1

;:::;X

n

]

(t

1

; :::; t

m

) =

m

Q

i=1

M

X

i

(t

i

)

.

16

Uwaga

Wiadomo, ·

ze (a

1

+ ::: + a

m

)

n

=

P

n

1

;:::;n

m

n1+:::+nm=n

n!

n

1

! ::: n

m

!

a

n

1

1

::: a

n

m

m

. Za÷

ó·

zmy, ·

ze wykonujemy

n

niezale·

znych do´swiadcze´n, przy czym ka·

zde do´swiadczenie mo·

ze si ¾

e zako´nczy´c jednym

z m wyników x

1

; :::; x

m

,

1

, przy czym p(x

i

) =

i

.

Niech N

i

oznacza zmienn ¾

a losow ¾

a

"zliczaj ¾

ac ¾

a" ilo´s´c wyników x

i

w serii m do´swiadcze´n. Otrzymujemy zatem wektor losowy

[N

1

; :::; N

m

]

. Mówimy, ·

ze ta m-wymiarowa zmienna ma rozk÷

ad wielomianowy je·

zeli

P (N

1

= n

1

; :::; N

m

= n

m

) =

n!

n

1

! ::: n

m

!

n

1

1

:::

n

m

m

.

Rozk÷

ad dwumianowy jest szczególnym przypadkiem rozk÷

adu wielomianowego.

Twierdzenie

Rozwa·

zmy zmienn ¾

a losow ¾

a S = X

1

+ ::: + X

N

. Za÷

ó·

zmy, ·

ze

1. X

x

1

x

2

:::

x

m

1

2

:::

m

2. N

P ( )

.

Zauwa·

zmy po pierwsze, ·

ze S = x

1

N

1

+ ::: + x

m

N

m

gdzie

m

P

i=1

N

i

= N

. Przy spe÷

nionych

za÷

o·

zeniach mamy:

1. N

1

; :::; N

m

s ¾

a niezale·

znymi zmiennymi losowymi o rozk÷

adzie Poissona

2.

i

=

i

.

Bardzo istotn ¾

a rol ¾

e odgrywa za÷

o·

zenie, ·

ze S ma z÷

o·

zony rozk÷

ad Poissona.

Dowód

M

[N

1

;:::;N

m

]

(t

1

; :::; t

m

) = E

"

e

m

P

i=1

t

i

N

i

#

=

1

P

n=0

E

"

e

n

P

i=1

t

i

M

i

jN = n

#

P (N = n) =

=

1

P

n=0

e

n

n!

P

n

1

;:::;n

m

n1+:::+nm=n

e

t

1

n

1

+:::+n

m

t

m

n!

n

1

! ::: n

m

!

n

1

1

:::

n

m

m

=

=

1

P

n=0

e

n

n!

P

n

1

;:::;n

m

n1+:::+nm=n

n!

n

1

! ::: n

m

!

(e

t

1

1

)

n

1

::: (e

t

m

m

)

n

m

=

=

1

P

n=0

e

n

n!

(

1

e

t

1

+ ::: +

m

e

t

m

)

n

= e

e [

1

e

t1

+:::+

m

e

tm

] =

= e

e

1 1

e

t1

::: e

m m

e

tm

= e

(

1

+:::+

m

)

e

1

e

t1

::: e

m

e

tm

=

= e

1

(

e

t1

1

) ::: e

m

(

e

tm

1

).

Wida´c zatem, ·

ze zmienne N

1

; :::; N

m

s ¾

a niezale·

zne oraz zmienna losowa N

i

ma rozk÷

ad

Poissona z parametrem

i

.

17

Przyk÷

ad

Niech X

1

2

3

0; 1

0; 4

0; 5

i N

P (

= 2)

. Wówczas S = N

1

+ 2N

2

+ 3N

3

, gdzie

N

1

p

1

, N

2

p

2

, N

3

p

3

. Wiadomo, ·

ze

1

= 2 0; 1 = 0; 2

,

2

= 2 0; 4 = 0; 8

,

3

= 2 0; 5 = 1

. St ¾

ad mamy

x

N

1

2N

2

3N

3

N

1

+ 2N

2

N

1

+ 2N

2

+ 3N

3

0

e

0;2

0; 819

e

0;8

0; 449

e

1

0; 368

0; 367731

0; 135325

1

0; 2 e

0;2

0; 164

0

0

0; 073636

0; 027098048

2

(0;2)

2

e

0;2

2!

0; 016

0; 8 e

0;8

0; 359

0

0; 301205

0; 11084344

3

(0;2)

3

e

0;2

3!

0; 001

0

e

1

0; 368

0; 059325

0; 157156608

4

(0;2)

4

e

0;2

4!

0; 00005

(0;8)

2

e

2

2!

0; 144

0

0; 12370245

0; 07262

5

(0;5)

5

e

0;2

5!

0; 000002

0

0

0; 023975898

0; 1196665705

:

Uwaga

Je´sli S = x

1

N

1

+ ::: + x

m

N

m

to

E [S] = x

1

E [N

1

] + ::: + x

m

E [N

m

] = x

1

1

+ ::: + x

m

m

= x

1

p(x

1

) + ::: + x

m

p(x

m

) =

=

m

P

i=1

x

i

p(x

i

) = p

1

oraz V ar [S] =

m

P

k=1

V ar [x

k

N

k

] =

m

P

k=1

x

2
k

V ar [N

k

]

.

Twierdzenie (wzór Panjera)

Je·

zeli S ma z÷

o·

zony rozk÷

ad Poissona gdzie N

i X przyjmuje warto´sci naturalne

1, 2, 3, ... to zachodzi równo´s´c

( ) f

S

(x) =

1

P

i=1

i

x

i

f

S

(x

i)

,

i

= p(i)

, x = 1; 2; 3:::.

Uwaga

Po prawej stronie wzoru ( ) wyst ¾

epuje jedynie sko´nczona suma sk÷

adników niezerowych.

Uwaga

Gdyby X mia÷rozk÷

ad o sko´nczonej ilo´sci warto´sci, to suma jest sko´nczona i sk÷

ada si ¾

e co

najwy·

zej z minfx; x

m

g sk÷adników, gdzie x

1

; :::; x

m

s ¾

a realizacjami zmiennej losowej X.

18

Dowód

Rozwa·

zmy warto´s´c oczekiwan ¾

a

(

) E [X

k

jX

1

+ ::: + X

n+1

= x]

dla k = 1; :::; n + 1.

Zauwa·

zmy, ·

ze wyra·

zenie (

)

jest sta÷

e ze wzgl ¾

edu na k. Z drugiej strony

E [X

1

+ ::: + X

n+1

jX

1

+ ::: + X

n+1

= x] = x =

n+1

P

k=1

E [X

k

jX

1

+ ::: + X

n+1

= x] =

= (n + 1) E [X

k

jX

1

+ ::: + X

n+1

= x]

E [X

k

jX

1

+ ::: + X

n+1

= x] =

x

n+1

dla k = 1; :::; n + 1

P (X

1

= i

jX

1

+ ::: + X

n+1

= x) =

P (X

1

=i^X

1

+:::+X

n+1

=x)

P (X

1

+:::+X

n+1

=x)

=

P (X

2

+:::+X

n+1

=x i) P (X

1

=i)

p

(n

1)

(x)

P (X

k

= i

jX

1

+ ::: + X

n+1

= x) =

p(i) p

(n)

(x i)

p

(n

1)

(x)

=

x

n+1

.

Przekszta÷

´cmy praw ¾

a stron ¾

e wzoru ( ). Mamy

1

P

i=1

i

x

i

1

P

k=0

P (N = k) p

(k)

(x

i) =

1

P

i=1

i

x

i

1

P

k=0

e

k

k!

p

(k)

(x

i) =

=

1

P

k=0

1

P

i=1

i

x

i

e

k

k!

p

(k)

(x

i) =

1

P

k=0

e

k

k!

1

P

i=1

i

x

i

p

(k)

(x

i) =

=

1

P

k=0

1
x

e

k

k!

1

P

i=1

i

i

p(i)p

(k)

(x

i) =

1

P

k=0

1
x

e

k+1

k!

1

P

i=1

ip(i)p

(k)

(x

i) =

=

1

P

k=0

1
x

e

k+1

k!

x

k+1

p

(k+1)

(x) =

1

P

k=0

e

k+1

(k+1)!

p

(k+1)

(x) =

1

P

k=1

e

k

k!

p

(k)

(x) =

=

1

P

k=0

e

k

k!

p

(k)

(x) = f

S

(x)

.

Przyk÷

ad

Niech X

1

2

3

0; 1

0; 4

0; 5

i N

P (

= 2)

.

Obliczy´c f

S

(5)

.

Wiadomo, ·

ze

S = N

1

+ 2N

2

+ 3N

3

, gdzie N

1

p

1

, N

2

p

2

, N

3

p

3

. Ponadto

1

= 2 0; 1 = 0; 2

,

2

= 2 0; 4 = 0; 8

,

3

= 2 0; 5 = 1

. St ¾

ad mamy

f

S

(0) = e

2

f

S

(1) =

1

P

i=1

i

1

i

f

S

(1

i) =

1

f

S

(1

1) =

1

e

2

= 0; 2e

2

f

S

(2) =

1
2

(1

1

f

S

(1) + 2

2

f

S

(0)) =

1
2

(0; 2 0; 2e

2

+ 2 0; 8 e

2

) = 0; 82e

2

f

S

(3) =

1
3

(

1

f

S

(2) + 2

2

f

S

(1) + 3

3

f

S

(0)) =

=

1
3

(0; 2 0; 82 e

2

+ 2 0; 8 0; 2 e

2

+ 3e

2

) =

3;484

3

e

2

=

871
750

e

2

f

S

(4) =

1
4

(

1

f

S

(3) + 2

2

f

S

(2) + 3

3

f

S

(1)) =

1
4

0; 2

871
750

e

2

+ 2 0; 8 0; 82e

2

+ 3 0; 2 e

2

=

8041

15000

e

2

f

S

(5) =

1
5

(

1

f

S

(4) + 2

2

f

S

(3) + 3

3

f

S

(2)) =

=

1
5

0; 2:

8041

15000

e

2

+ 2 0; 8

871
750

e

2

+ 3 0; 82 e

2

0; 8850693333e

2

.

19

Twierdzenie

Je·

zeli S ma z÷

o·

zony rozk÷

ad Poissona z parametrem

i rozk÷

adem pojedynczej szkody p(x),

to lim

!1

S

p

1

p

p

2

F

= N (0; 1)

.

Dowód

Skorzystamy z metody funkcji generuj ¾

acej momenty. Mamy

M

S

p1

p

p2

(t) = E

"

e

t

S

p1

p

p2

#

= M

S

t

p

p

2

e

t p1

p

p2

= e

h

M

X

t

p

p

1

i

e

p1

p

p2

t

ln M

S

p1

p

p2

(t) =

h

M

X

t

p

p

2

1

i

p

1

p

p

2

t =

=

1 + p

1

t

p

p

2

+

p

2

2!

t

2

(

p

p

2

)

2

+

p

3

3!

t

p

p

2

3

+ :::

1

p

1

p

p

2

t =

=

p

1

t

p

p

2

+

p

2

2!

t

2

p

2

+

p

3

3!

t

3

3

2

p

3

2

2

+ :::

p

1

p

p

2

t =

=

p

2

2!

t

2

p

2

+

p

3

3!

t

3

3

2

p

3

2

2

+ ::: =

t

2

2

+

t

3

p

3

3!

1

2

p

3

2

2

+ :::

ln M

S

p1

p

p2

(t) =

t

2

2

+

t

3

p

3

3!

1

2

p

3

2

2

+ :::

lim

!1

ln M

S

p1

p

p2

(t) =

t

2

2

=

) M

S

p1

p

p2

(t)

!1

! e

t2

2

= M

N (0;1)

(t)

.

Uwaga

Niech g(x) =

( )

x

1

e

x

dx

dla x > 0, h(x) =

( )

(x

x

0

)

1

e

(x x

0

)

dla x > x

0

.

Wówczas

E [ ( ; )] =

V ar [ ( ; )] =

2

E (X

EX)

3

= ln M

( ; )

(t)

000
t=0

=

h

ln

t

i

000

t=0

=

h

2

(

t)

3

i

t=0

=

2

3

.

Aproksymacja przesuni ¾

etego rozk÷

adu gamma polega na tym, ·

ze dobieramy wspó÷

czynniki

,

, x

0

w ten sposób, by pierwsze trzy momenty centralne w rozk÷

adzie aproksymowanym

i aproksymuj ¾

acym by÷

y równe, tzn. E [H] = x

0

+

, V ar [H] =

2

oraz E [(H

EX)

3

] =

2

3

.

Zatem

=

V arX

2E[(X EX)

3

]

=

h

2V arX

E[(X EX)

3

]

i

2

V arX =

4(V arX)

3

[E[(X EX)

3

]]

2

x

0

= EX

.

20

Przyk÷

ad

Niech S b ¾

edzie z÷

o·

zonym rozk÷

adem Poissona o parametrze

= 4

oraz rozk÷

adzie

pojedynczej szkody 2e

2x

. Wyznaczy´c przesuni ¾

ety rozk÷

ad gamma aproksymuj ¾

acy dany z÷

o·

zony

rozk÷

ad Poissona.

Wiadomo, ·

ze

E [S] = p

1

= 4

1
2

= 2

V ar [S] = p

2

= 4

2
4

= 2

E (S

ES)

3

= 3

2 =

+ x

0

2 =

2

3 =

2

3

2
3

=

2

=

)

=

4
3

= 2

16

9

=

32

9

x

0

= 2

32

9

3
4

= 2

8
3

=

2
3

.

Zatem aproksymuj ¾

acym rozk÷

adem jest H

32

9

;

4
3

;

2
3

.

ELEMENTY TEORII RUINY

Zajmowa´c b ¾

edziemy si ¾

e w tym rozdziale procesem stochastycznym postaci

U (t) = u + ct

S(t)

, t

0

, u

0

, c > 0.

S(t) = X

1

+ ::: + X

N (t)

jest funkcj ¾

a liniow ¾

a opisuj ¾

ac ¾

a proces szkodowy. Jest to zatem suma

wyp÷

at do momentu t. Proces U (t) nazywa si ¾

e procesem nadwy·

zki ubezpieczyciela. u oznacza

kapita÷pocz ¾

atkowy za´s c intensywno´s´c wyp÷

acania sk÷

adek.

Niech T oznacza moment ruiny, tzn. T = infft : U(t) < 0g. Przyjmujemy ponadto T = 1

gdy dla dowolnego t

0 U (t)

0

. Zasadniczym problemem jest badanie prawdopodobie´nstwa

P (T <

1) = (u). Szczególnym tego przypadkiem jest zajmowanie si¾

e prawdopodobie´nstwem

P (T < t

0

)

, t

0

> 0

.

Zak÷

ada´c b ¾

edziemy, ·

ze N (t) jest procesem Poissona, tzn.

P (N (t + h)

N (t) = k

jN(s); s

t) =

e

h

( h)

k

k!

. Niech T

1

; T

2

; :::

b ¾

ed ¾

a momentami czasu,

w których wyst ¾

api÷

y kolejne szkody.

Niech W

1

= T

1

, W

2

= T

2

T

1

, W

3

= T

3

T

2

,

W

k

= T

k

T

k 1

. Wtedy P (W

k

> h

jT

k 1

= t) = P (N (t + h)

N (t) = 0

jT

k 1

= t) = e

h

.

Wobec tego S(t) nazywamy z÷

ozonym procesem Poissona.

Zauwa·

zmy, ·

ze E [S(t)] = tp

1

. B ¾

edziemy zak÷

ada´c, ·

ze c > p

1

, czyli c = (1 + ) p

1

,

> 0

.

Rozwa·

zmy równanie

( )

+ ct = M

X

(t)

,

21

gdzie M

X

(t)

jest funkcj ¾

a generuj ¾

ac ¾

a momenty rozk÷

adu pojedynczej szkody. O funkcji M

X

(t)

zak÷

adamy, ·

ze istnieje

> 0

, ·

ze t 2 ( 1; ) oraz lim

t!

M

X

(t) =

1. Wnioskujemy, ·

ze równanie

( )

równowa·

zne jest równaniu

(

)

+ (1 + ) p

1

t = M

X

(t)

.

Twierdzenie

Równanie

(

) 1 + (1 + )p

1

t = M

X

(t)

, t 2 ( 1; )

posiada dok÷

adnie jedno rozwi ¾

azanie niezerowe R.

Rozwi ¾

azanie to nazywamy

wspó÷

czynnikiem dostosowania (adjustment coe¢ cient).

Dowód

Zauwa·

zmy, ·

ze M

0

X

(t) = E Xe

tX

> 0

, M

00

X

(t) = E X

2

e

Xt

> 0

, M

X

(0) = 1

, M

0

X

(0) = p

1

.

Poniewa·

z funkcja po lewej stronie równanie (

)

jest liniowa i w punkcie t = 0 przyjmuje

warto´s´c 1, wi ¾

ec wobec faktu, ·

ze M

X

(t)

jest rosn ¾

aca i wypuk÷

a oraz M

X

(0) = 1

otrzymujemy,

·

ze istnieje dok÷

adnie jedno dodatnie rozwi ¾

azanie równania (

)

.

Przyk÷

ady

1.

Wyznaczymy wspó÷

czynnik dostosowania w przypadku, gdy zmienna losowa X ma

rozk÷¾

ad wyk÷

adniczy, tzn. f

X

(x) = e

x

1

(0;1)

(x)

. Korzystaj ¾

ac ze wzoru (

)

mamy

1 + (1 + )

1

t =

t

2

t + (1 + )(

t) =

2

+ (1 + ) (

t) = 0

+

t +

t = 0

t (

1) +

= 0

t =

1+

.

Zatem w przypadku rozk÷

adu wyk÷

adniczego R =

1+

.

2. Je·

zeli X jest zmienn ¾

a losow ¾

a o rozk÷

adnie zdegenerowanym, tzn. P (X = a) = 1, wówczas

korzystaj ¾

ac ze wzoru (

)

otrzymujemy równanie postaci

1 + (1 + )at = e

at

.

Równania tego w dowolnym przypadku nie da si ¾

e rozwi ¾

aza´c w sposób dok÷

adny, dlatego te·

z

w celu znalezienia wspó÷

czynnika dostosowania stosujemy metod ¾

e kolejnych przybli·

ze´n.

Twierdzenie (o prawdopodobie´

nstwie ruiny)

Zachodzi równo´s´c

(#)

(u) =

e

Ru

E

[

e

RU (T )

jT <1

]

.

Jest to wzór na prawdopodobie´nstwo ruiny w sko´nczonym horyzoncie czasowym.

22

Uwaga

Prawdopodobie´nstwo ruiny w ogólnym przypadku nie daje si ¾

e policzy´c w sposób dok÷

adny,

co wynika w g÷

ównej mierze ze skomplikowanej struktury zmiennej losowej U (T ). Istniej ¾

a

jednak pewne oszacowania prawdopodobie´nstwa ruiny:

1.

(u) < e

Ru

(= U(T ) < 0 ()

U (T ) > 0

() e

RU (T )

> 1

Czasami przyjmuje si ¾

e pewne przybli·

zenie, bo warto´s´c w mianowniku (#) jest trudna do

policzenia i przyjmujemy

(u)

e

Ru

.

2. Za÷

ó·

zmy, ·

ze 9

m

P

X

(m) = 1

, tzn. P (X

m) = 1

. Wóczas wszystkie pojedyncze szkody

s ¾

a niewi ¾

eksze od m. Moment ruiny jest to pierwsza chwila, w której nadwy·

zka jest ujemna.

Przed ruin ¾

a nadwy·

zka jest dodatnia, wi ¾

ec zaistania÷

a szkoda o warto´sci X

m

implikuje, ·

ze

U (T )

m

, a zatem e

RU (T )

e

Rm

<

1. Poniewa·

z

RU (T )

Rm

, wi ¾

ec

E e

RU (T )

jT

1

e

Rm

oraz

(u) =

e

Ru

E

[

e

RU (T )

jT <1

]

e

Ru

e

Rm

= e

R(u+m)

.

Zatem w przypadku, gdy warto´sci szkoód s ¾

a ograniczone przez sta÷¾

a m, to otrzymujemy

oszacowanie

(u)

e

R(u+m)

.

3. Poka·

zemy, ·

ze lim

!0

+

(u) = 1

zachodzi dla

> 0

oraz udowodnimy, ·

ze nie ma sensu

rozwa·

zania przypadku, gdy

0

. We´zmy c = (1 + ) p

1

oraz

> 0

. Wówczas, je·

zeli

! 0,

to R ! 0. Poniewa·

z U (T ) < 0, wi ¾

ec

RU (T )

! 0

+

oraz e

RU (T )

! 1. Zatem je´sli

! 0, to

e

Ru

! 1 oraz E e

RU (T )

jT < 1 ! 1. St ¾

ad lim

!0

+

(u) = 1

.

Niech teraz

0

. Wtedy c

p

1

. Dla c

1

< c

2

mamy wówczas

c

1

(u)

c

2

(u)

, a st ¾

ad

wynika, ·

ze

9

c

c

p

1

^ (u) = 1.

Przyk÷

ad

Obliczymy prawdopodobie´nstwo ruiny w przypadku, gdy X ma rozk÷

ad wyk÷

adniczy

z parametrem

. Wiadomo, ·

ze w tym przypadku R =

1+

. Niech U (t) tu·

z przed momentem

ruiny ma warto´s´c ^

u

0

. Policzmy

P ( U (T ) > y) = P (X > ^

u + y

jX > ^u) =

e

( ^

u+y)

e

^

u

= e

y

.

Zatem P ( U (T ) > y) = e

y

, wi ¾

ec P ( U (T )

y) = 1

e

y

. Wnioskujemy st ¾

ad, ·

ze

U (T )

ma rozk÷

ad wyk÷

adniczy z parametrem . Wobec tego

E e

RU (T )

jT < 1 = M

U (T )

(R) =

R

.

Czyli

(u) =

e

Ru

(

R)

=

e

1+

u

(

R)

=

e

1+

u

(

1+

)

=

1

1+

e

1+

u

.

Zatem gdy

! 0, to (u) ! 1.

23

Rozwa·

zmy

teraz

proces

nadwy·

zki

ubezpieczyciela

z

czasem

dyskretnym,

tzn.

U

n

= u + nc

S(N )

, n = 0; 1; 2; :::. Rezygnujemy tutaj z za÷

o·

zenia, ·

ze S

n

jest z÷

o·

zonym

procesem Poissona. Rozwa·

zmy teraz

( ) U

n

= u + nc

(W

1

+ ::: + W

n

)

.

O zmiennych losowych W

k

za÷

ó·

zmy, ·

ze s ¾

a niezale·

zne i o identycznym rozk÷

adzie. Wówczas

S(n)

oznacza ilo´s´c wyp÷

aconych szkód do chwili n. Zmienne W

k

mo·

zna traktowa´c jako sum ¾

e

wyp÷

aconych szkód w danym roku (je´sli za÷

o·

zymy, ·

ze W

k

maj ¾

a rozk÷

ad Poissona z parametrem

, to otrzymamy poprzednio rozwa·

zany proces).

Podobnie jak dla przypadku ci ¾

ag÷

ego mo·

zna zde…niowa´c moment i prawdopodobie´nstwo

ruiny:

^

T = min

fn : U

n

< 0

g

(u) = P

^

T <

1 .

Wprowad´zmy oznaczenia:

= E [W

k

]

oraz za÷

ó·

zmy, ·

ze c >

jest intensywno´sci ¾

a wp÷

ywania

sk÷

adki, która jest niemniejsza ni·

z warto´s´c oczekiwana W

k

. Rozwa·

zmy równanie postaci

(

) e

rc

M

W

(r) = 1

.

Poka·

zemy, ·

ze równanie (

)

posiada dok÷

adnie 1 rozwi ¾

azanie dodatnie.

To niezerowe

rozwi ¾

azanie b ¾

edziemy nazywa´c wspó÷

czynnikiem dostosowania dla przypadku dyskretnego

i oznaczamy symbolem ^

R

.

Za÷

ó·

zmy, ·

ze W

P ( ; P (x))

, czyli W jest z÷

o·

zonym rozk÷

adem Poissona (wówczas S(n)

jest równie·

z z÷

o·

zonym rozk÷

adem Poissona). Wówczas równanie (

)

mo·

zna zapisa´c w postaci

rc + ln M

W

(r) = 0

M

W

(r) = e

[M

X

(r) 1]

rc +

[M

X

(r)

1] = 0

()

+ cr = M

X

(r)

.

Zatem otrzymali´smy znane z poprzedniego przypadku równanie na wspó÷

czynnik

dostosowania.

W przypadku ogólnym rozwa·

zamy dowolne rozk÷¾

ady zmiennych losowych W , a co za tym

idzie rozk÷

ady zmiennej losowej S z czasem dyskretnym.

Zbadajmy funkcj ¾

e f (r) = e

rc

M

W

(r) = e

rc

E e

rW

.

Funkcja ta ma nast ¾

epuj ¾

ace

elementarne w÷

asno´sci:

1. f (0) = 1.

2. f

0

(r) = E e

(W

c)r 0

= E (W

c) e

(W

c)r

oraz f

0

(0) = E [W

c] =

c < 0

.

Przyjmijmy, ·

ze zmienna losowa W przyjmuje z prawdopodobie´nstwem dodatnim warto´sci

wi ¾

eksze ni·

z c. Wówczas lim

r!1

f

0

(r) =

1.

3. f

00

(r) = E (W

c)

2

e

(W

c)r

> 0

.

Zatem f jest funkcj ¾

a rosn ¾

ac ¾

a oraz wypuk÷¾

a.

St ¾

ad wnioskujemy, ·

ze równanie (

)

ma

dok÷

adnie jedno rozwi ¾

azanie, którym jest R.

24

Twierdzenie (o prawdopodobie´

nstwie ruiny w przypadku dyskretnym)

Zachodzi równo´s´c:

^ (u) =

e

^

Ru

E

[

e

^

RU (T )

jT <1

]

.

Policzymy wspó÷

czynnik dostosowania w przypadku, gdy W

N ( ;

2

)

. Wobec równania

(

)

mamy

e

rc

M

W

(r) = 1

()

rc + ln M

W

(r) = 0

()

rc + r +

1
2

2

r

2

= 0

()

()

c +

+

1
2

2

r = 0

() ^

R =

2(c

)

2

.

Za÷

ó·

zmy teraz, ·

ze W jest zmienn ¾

a losow ¾

a o dowolnym rozk÷

adzie. Wówczas z równania na

wspó÷

czynnik dostosowania mamy

rc + ln M

W

(r) = 0

rc + ln E e

rW

= 0

E e

rW

= E

h

1 + rW +

r

2

W

2

2!

+

r

3

W

3

3!

+ :::

i

= 1 + r +

r

2

p

2

2

+ :::

rc + ln 1 + r +

r

2

p

2

2

+ ::: =

rc + r +

r

2

p

2

2

+ :::

r +

r2p2

2

+:::

2

2

+ ::: = 0

rc + r +

r

2p2

2

r

2

2

= 0

c +

+

1
2

rp

2

1
2

r

2

= 0

c +

+

1
2

r (p

2

2

) = 0

c +

+

1
2

r

2

= 0

czyli ^

R

2(

c)

2

.

Zatem wszystkie inne zmienne losowe o dowolnym rozk÷

adzie maj ¾

a

przybli·

zon ¾

a posta´c wspó÷

czynnika dostosowania do rozk÷

adu normalnego.

Uogólnimy model dyskretny na pewien przypadek zale·

zno´sci zmiennych losowych W

i

.

Rozwa·

zmy model z autoregresj ¾

a pierwszego rodzaju.

Niech Y

1

; :::; Y

n

b ¾

edz ¾

a zmiennymi

losowymi i.i.d.

Niech W

i

= Y

i

+ aW

i 1

, i = 1; :::; n, gdzie a 2 ( 1; 1), W

0

= w

oraz

E [W

i

] =

< c

. St ¾

ad mamy

E [W

i

] = E [Y

i

] + aE [W

i

]

E [Y

i

] = E [W

i

]

aE [W

i 1

] < (1

a) c

W

1

= Y

1

+ aw

W

2

= Y

2

+ a (Y

1

+ aw) = Y

2

+ aY

1

+ a

2

w

W

3

= Y

3

+ a (Y

2

+ aY

1

+ a

2

w) = Y

3

+ aY

2

+ a

2

Y

1

+ a

3

w

W

i

= Y

i

+ aY

i 1

+ a

2

Y

i 2

+ ::: + a

i 1

Y

1

+ a

i

w

.

Uwzgl ¾

edniaj ¾

ac fakt, i·

z U

n

= u + cn + S

n

oraz

S

n

= W

1

+ ::: + W

n

S

1

= Y

1

+ aw

S

2

= Y

1

+ aw + Y

2

+ aY

1

+ a

2

w = Y

2

+ (1 + a) Y

1

+ (a

2

+ a) w

S

3

= Y

2

+ (1 + a) Y

1

+ (a + a

2

) w + Y

3

+ aY

2

+ a

2

Y

1

+ a

3

w =

25

= Y

3

+ (1 + a) Y

2

+ (1 + a + a

2

) Y

1

+ (a + a

2

+ a

3

) w

S

n

= Y

n

+

(1 a)

2

1 a

Y

n 1

+

1 a

3

1 a

Y

n 2

+ ::: +

1 a

n

1 a

Y

1

+

1 a

n

1 a

aw

otrzymujemy

^

U

n

= U

n

a

1 a

W

n

^

U

n

= u + cn

Y

n

+

(1 a)

2

1 a

Y

n 1

+

1 a

3

1 a

Y

n 2

+ ::: +

1 a

3

1 a

Y

1

+

1 a

3

1 a

aw

+

a

1 a

(Y

n

aY

n 1

+ a

2

Y

n 2

+ ::: + a

n 1

Y

1

+ a

n

w)

^

U

n

= u + cn

Y

n

1 a

+

Y

n

1

1 a

+ ::: +

Y

1

1 a

a

1 a

^

U

n

= u

a

1 a

w + cn

Y

1

1 a

+

Y

2

1 a

+ ::: +

Y

n

1 a

^

U

n

= ^

u + cn

Y

1

1 a

+

Y

2

1 a

+ ::: +

Y

n

1 a

.

Wnioskujemy zatem, ·

ze R jest rozwi ¾

azaniem nast ¾

epuj ¾

acego równania:

e

cr

M

Y

1

a

(r) = 1

.

Ponadto

^

T = min

fn : U

n

< 0

g

(u; w) =

e

^

R ^

U

E

[

e

^

R ^

U ( ^

T )

j ^

T <1

]

.

26