Wstęp

2

1. Wynikanie semantyczne

3

2. Reguły inferencyjne i pojęcie dowodu formalnego

5

3. System dedukcji naturalnej

9

4. Dowody przez dodatkowe założenie

16

5. Formy zdaniowe

17

6. Kwantyfikatory

19

Bibliografia

21

Wynikanie logiczne

i elementy rachunku kwantyfikatorów

2

Wstęp

W niniejszej części materiałów przedstawimy ciąg dalszy rozważań dotyczących
rachunku zdań. Zdefiniowane zostanie — a także scharakteryzowane
odpowiednimi twierdzeniami — pojęcie wynikania semantycznego. Na tej bazie
wprowadzimy analogiczne pojęcie, jakim jest wynikanie syntaktyczne. Zdefiniujemy
zatem pojęcie dowodu formalnego wprost i nie wprost. Wprowadzimy pewien
układ reguł dedukcji naturalnej zupełny wobec prezentowanego w poprzednim
module semantycznego ujęcia rachunku zdań. Zdefiniowane zostanie też pojęcie
formy zdaniowej i wprowadzone kwantyfikatory. Omówimy pojęcia zmiennej
wolnej i zmiennej związanej. Zaprezentujemy przykładowe prawa rachunku
kwantyfikatorów.

3

1. Wynikanie semantyczne

Powiemy, że

formuła

α

wynika

semantycznie ze zbioru formuł

X, co będziemy oznaczać

X ׀= α, jeżeli formuła α jest prawdziwa dla wszystkich wartościowań dających
wartość 1 dla wszystkich formuł ze zbioru X.

Przykład 1

Rozważmy formułę p ⇒ q oraz zbiór formuł X = {p, q}. Rozważmy wszystkie
wartościowania v, w których są prawdziwe wszystkie formuły (zmienne) ze zbioru
X. Mamy wartościowanie v(p) = 1 oraz v(q) = 1. Ale wtedy mamy również
w(p ⇒ q) = 1. Zatem zdanie p ⇒ q wynika ze zbioru X = {p, q} ({p, q} ׀= p ⇒ q).

Przykład 2

Rozważmy formułę ¬(¬p ∧ q) oraz zbiór formuł X = {p, ¬q}. Rozważmy
wszystkie wartościowania v, w których są prawdziwe wszystkie zdania ze zbioru
X. Mamy wartościowanie v(p) = 1 oraz v(q) = 0. Dla tego wartościowania
jest: w(¬(¬p ∧ q)) = 1. Zatem formuła ¬(¬p ∧ q) wynika ze zbioru
X = {p, ¬q} ({p, ¬q} ׀= ¬(¬p ∧ q)).

Z definicji wynikania można wyprowadzić warunek na fakt, że dane zdanie nie
wynika z odpowiedniego zbioru zdań.

Powiemy, że

formuła

α

nie wynika

semantycznie ze zbioru formuł

X (X ׀≠ α), jeżeli dla

pewnego wartościowania v wszystkie zdania ze zbioru X

są prawdziwe, zaś zdanie

α jest fałszywe (w(α) = 0).

Przykład 3

Rozważmy formułę ¬p ∧ q oraz zbiór formuł X = {p, q}. Rozważmy wszystkie
wartościowania v, w których są prawdziwe wszystkie zdania ze zbioru X.
Mamy wartościowanie v(p) = 1 oraz v(q) = 1. Dla tego wartościowania jest:
w(¬p ∧ q) = 0. Zatem formuła ¬p ∧ q nie wynika ze zbioru X = {p, q} ({p, q} ׀≠ ¬p ∧ q).

Zachodzą następujące twierdzenia:

Twierdzenie 1

Formuła α jest tautologią wtedy i tylko wtedy, gdy wynika semantycznie ze zbioru
pustego. Symbolicznie ∅ ׀= α lub krócej ׀= α (bez wypisywania zbioru przed
symbolem wynikania).

Twierdzenie 2

Formuła

α

wynika

semantycznie

ze

skończonego

zbioru

formuł

X = {α

1

, α

2

, ..., α

n

} (X ׀= α) wtedy i tylko wtedy, gdy implikacja (α

1

∧ α

2

∧ ... ∧ α

n

) ⇒ α

jest tautologią.

4

Dowód

Załóżmy, że formuła α wynika semantycznie ze skończonego zbioru formuł
X = {α

1

, α

2

, ..., α

n

}. Wtedy dla dowolnego wartościowania, dla którego formuły

α

1

, α

2

, ..., α

n

przyjmują wartość 1, również formuła α przyjmuje wartość 1.

Rozważmy implikację (α

1

∧ α

2

∧ ... ∧ α

n

) ⇒ α. Wszystkie wartościowania możemy

podzielić na dwie grupy: takie, dla których wartość koniunkcji α

1

∧ α

2

∧ ... ∧ α

n

wynosi 0 oraz takie, dla których wartość tej koniunkcji jest równa 1. W pierwszym
przypadku mamy fałszywy poprzednik rozpatrywanej implikacji, jest ona
zatem prawdziwa. W drugim przypadku zauważmy, że jeżeli wartość koniunkcji

α

1

∧ α

2

∧ ... ∧ α

n

jest równa 1, to każda z formuł α

1

, α

2

, ..., α

n

musi również

przyjmować wartość 1. Możemy wtedy skorzystać z założenia, że również formuła

α (następnik rozpatrywanej implikacji) ma wartość 1, zatem implikacja jest
także prawdziwa. Widzimy, że dla dowolnych wartościowań wartość implikacji
(α

1

∧ α

2

∧ ... ∧ α

n

)

⇒ α jest równa 1. Zatem jest ona tautologią.

Załóżmy teraz, że implikacja (α

1

∧ α

2

∧ ... ∧ α

n

) ⇒ α jest tautologią. Rozważmy

wszystkie wartościowania, dla których formuły ze zbioru X = {α

1

, α

2

, ..., α

n

} mają

wartość 1. Oczywiście, dla tych wartościowań formuła α nie może mieć wartości
0, gdyż byłoby to sprzeczne z tautologicznością implikacji (α

1

∧ α

2

∧ ... ∧ α

n

) ⇒ α.

Zatem formuła α musi mieć wartość 1. Oznacza to oczywiście, że formuła α wynika
semantycznie ze skończonego zbioru formuł X = {α

1

, α

2

, ..., α

n

} (X ׀= α).

5

2. Reguły inferencyjne

i pojęcie dowodu formalnego

W dotychczasowych rozważaniach przedstawiliśmy tzw. semantyczne ujęcie
rachunku zdań. Oznacza to, że odwoływaliśmy się do pojęcia wartości logicznych,
wartościowania zmiennych i wartości formuł dla danych wartościowań zmiennych.
Przedstawimy teraz tak zwane syntaktyczne ujęcie omawianego rachunku
logicznego. W ujęciu tym nie odwołujemy się do pojęć semantycznych (wartości
logicznych itp.), ale wykonujemy wnioskowanie, wyprowadzając (dedukując) jedne
formuły z innych.

Odpowiednikiem omawianego wyżej pojęcia wynikania semantycznego jest tutaj
pojęcie wynikania syntaktycznego związane ściśle z pojęciami reguł inferencyjnych
oraz dowodu formalnego.

Reguły inferencyjne

to schematy pozwalające wyprowadzać (dedukować) formuły

z innych formuł. Schematy te przedstawiać będziemy w następującej postaci:

, gdzie formuły α

1

, α

2

, ..., α

n

będziemy nazywać

przesłankami

, zaś

formułę β —

wnioskiem

. Ogólnie reguła o schemacie:

pozwala z for-

muł (przesłanek) α

1

, α

2

, ..., α

n

wyprowadzić (wydedukować) formułę β (wniosek).

Dla uproszczenia zapisu będziemy czasem stosować następującą notację

dla symetrycznych par reguł postaci:

oraz .

Przykład 4

Jako przykład przedstawimy reguły

E

liminacji

K

oniunkcji (

EK

) o schematach:

oraz

. Reguły te pozwalają z dowolnej koniunkcji α ∧ β (zauważmy, że α

oraz β mogą być dowolnymi formułami) wyprowadzać czynniki tej koniunkcji.

I tak — jeżeli rozważymy formułę (¬r ∨ p) ∧ ¬(¬p ∨ q ⇒ s) — to na mocy reguł

EK

możemy z tej formuły wyprowadzić oba jej czynniki: ¬r ∨ p oraz ¬(¬p ∨ q ⇒ s).

Oczywiście, dane reguły nie zawsze możemy stosować do dowolnych formuł.
Powyższych reguł

EK

nie możemy zastosować na przykład do formuły

¬(¬p ∨ q ⇒ s), gdyż ta nie jest koniunkcją.

Przykład 5

Reguły

E

liminacji

A

lternatywy (

EA

) mają następujące schematy:

,

.

6

Reguły te pozwalają z alternatywy i negacji jednego z jej składników wyprowadzić
drugi składnik alternatywy. I tak — jeżeli rozważymy formułę (¬p ⇒ q) ∨ (q ⇒ s)
oraz formułę ¬(¬p ⇒ q) — to na mocy jednej z reguł

EA

możemy z tych formuł

wyprowadzić formułę (q ⇒ s). Oczywiście — jak w poprzednim przypadku
— dane reguły nie zawsze możemy stosować do dowolnych formuł.

Przykład 6

Z pewnych względów wzbogacamy język rozważań o stałą logiczną reprezentującą
pojęcie sprzeczności, oznaczaną symbolem

⊥. W dalszych rozważaniach będziemy

korzystać z następującej reguły

D

ołączania

S

przeczności (

DS

):

DS

:

.

Jeżeli w ciągu dowodowym mamy jako przesłanki formułę i jej negację, to możemy
do dowodu dopisać symbol sprzeczności.

Za pomocą pojęcia reguł inferencyjnych możemy już zdefiniować — kluczowe
w ujęciach syntaktycznych — pojęcie dowodu formalnego formuły. Podamy
definicje dwóch różnych typów dowodów, a mianowicie dowodu wprost i dowodu
nie wprost.

Dowodem formalnym wprost formuły

α na gruncie reguł ze zbioru ℜ oraz formuł

ze zbioru X nazywamy skończony ciąg formuł ϕ

1

, ϕ

2

, ..., ϕ

n

o następujących

własnościach:
1. Ostatnia formuła ciągu dowodowego jest formułą dowodzoną (ϕ

n

= α).

2. Każda formuła ciągu dowodowego jest albo elementem zbioru X, albo wnioskiem

z wcześniej wyprowadzonych formuł dowodu w myśl pewnej reguły ze zbioru ℜ.

Przykład 7

Weźmy zbiór reguł

ℜ = {

,

,

,

} oraz

jednoelementowy zbiór formuł X = {(¬p ∨ q) ∧ ¬q}.

Rozważmy następujący ciąg formuł:
1. ϕ

1

= (¬p ∨ q) ∧ ¬q.

2. ϕ

2

= ¬p ∨ q.

3. ϕ

3

= ¬q.

4. ϕ

4

= ¬p.

Zauważmy, że każda formuła powyższego ciągu jest albo elementem zbioru X, albo
wnioskiem z wcześniejszych formuł ciągu w myśl pewnej reguły ze zbioru ℜ.

I tak kolejno: formuła ϕ

1

jest elementem zbioru X, formuły ϕ

2

i ϕ

3

są wnioskami

z formuły ϕ

1

w myśl reguł

EK

, formuła ϕ

4

jest wnioskiem z formuł ϕ

2

i ϕ

3

w myśl

jednej z reguł

EA

.

Możemy zatem stwierdzić, że ciąg formuł ϕ

1

, ϕ

2

, ϕ

3

, ϕ

4

jest dowodem wprost

formuły ¬p (ϕ

4

) na gruncie zbiorów ℜ oraz X.

Dowodem formalnym nie wprost formuły

α na gruncie reguł ze zbioru ℜ oraz formuł ze zbioru

X nazywamy skończony ciąg formuł ϕ

1

, ϕ

2

, ..., ϕ

n

o następujących własnościach:

7

1. Ostatnia formuła ciągu dowodowego jest symbolem sprzeczności (ϕ

n

= ⊥).

2. Każda formuła ciągu dowodowego jest albo elementem zbioru X, albo negacją

formuły α, albo wnioskiem z wcześniej wyprowadzonych formuł dowodu w myśl
pewnej reguły ze zbioru ℜ.

Przykład 8

Rozważmy zbiór reguł

ℜ = {

,

,

,

,

}

oraz jednoelementowy zbiór formuł X = {(p ∨ q) ∧ ¬q}. Podany niżej dowód jest

dowodem nie wprost dla formuły p.
1. ϕ

1

= (p ∨ q) ∧ ¬q.

2. ϕ

2

= ¬p.

3. ϕ

3

= p ∨ q.

4. ϕ

4

= ¬q.

5. ϕ

5

= p.

6. ϕ

6

= ⊥.

Zauważmy, że każda formuła powyższego ciągu jest albo negacją dowodzonej
formuły, albo elementem zbioru X, albo wnioskiem z wcześniejszych formuł ciągu
w myśl pewnej reguły ze zbioru ℜ.

I tak kolejno: formuła ϕ

1

jest elementem zbioru X, formuła ϕ

2

jest negacją

dowodzonej formuły p, formuły ϕ

3

i ϕ

4

są wnioskami z formuły ϕ

1

w myśl reguł

EK

, formuła ϕ

5

jest wnioskiem z formuł ϕ

3

i ϕ

4

w myśl jednej z reguł

EA

. Natomiast

symbol sprzeczności ⊥ (ϕ

6

) jest wnioskiem z formuł ϕ

2

i ϕ

5

w myśl reguły

DS

.

Możemy zatem stwierdzić, że ciąg formuł ϕ

1

, ϕ

2

, ϕ

3

, ϕ

4

, ϕ

5

, ϕ

6

jest dowodem nie

wprost formuły p na gruncie zbiorów ℜ oraz X.

Powiemy, że

formuła

α

wynika syntaktycznie

ze zbioru X na gruncie reguł ze zbioru ℜ

(co będziemy oznaczać X ׀−

ℜ

α), jeżeli formuła α ma dowód (wprost lub nie wprost)

na gruncie reguł ze zbioru ℜ oraz formuł ze zbioru X.

Dla uproszczenia — jeżeli X = {α

1

, α

2

, ..., α

n

}, to będziemy stosować zapis

α

1

, α

2

, ..., α

n

׀−

ℜ

α. Formuły α

1

, α

2

, ..., α

n

nazywamy

przesłankami

lub

założeniami

,

zaś formułę α

wnioskiem

.

Przykład 9

Z

przykładu 7

wynika, że

(¬p ∨ q) ∧ ¬q ׀−

ℜ

¬p. Ale także, jeżeli przyjrzymy się

uważnie temu przykładowi, widać, że prawdą jest również: (¬p ∨ q) ∧ ¬q ׀−

ℜ

¬q oraz

(¬p ∨ q) ∧ ¬q ׀−

ℜ

¬p ∨ q.

Twierdzenie 3

Dla dowolnej formuły α i dowolnego niepustego układu reguł ℜ spełnione jest:

α ׀−

ℜ

α.

8

Dowód

Aby udowodnić powyższe twierdzenie, trzeba wykazać istnienie odpowiedniego
ciągu formuł

α

1

, α

2

, ..., α

n

, spełniającego warunki dla dowodu wprost lub dowodu

nie wprost. W przypadku dowodu wprost mamy następujące warunki:
1. Ostatnia formuła ciągu dowodowego jest formułą dowodzoną (α

n

= α).

2. Każda formuła ciągu dowodowego jest formułą α albo wnioskiem z wcześniej

wyprowadzonych formuł dowodu w myśl pewnej reguły ze zbioru ℜ.

Rozważmy jednoelementowy ciąg formuł:

α

1

= α.

Zauważmy, że tak podany jednoelementowy ciąg spełnia oba warunki wymagane
dla ciągu dowodowego dla danej formuły. Zatem — ponieważ istnieje odpowiedni
dowód wprost — uzyskaliśmy, że α ׀−

ℜ

α.

Twierdzenie 4

Dla dowolnego niepustego zbioru formuł X, dowolnej formuły α ze zbioru X
i dowolnego niepustego układu reguł ℜ spełnione jest:

X ׀−

ℜ

α.

Dowód opiera się na poprzednim twierdzeniu.

Zachodzi również następujące twierdzenie o monotoniczności:

Twierdzenie 5

Dla dowolnych formuł α, β, γ i dowolnego niepustego układu reguł ℜ, jeżeli

α ׀−

ℜ

β oraz β ׀−

ℜ

γ, to spełnione jest również α ׀−

ℜ

γ.

Dowód

Załóżmy, że

α ׀−

ℜ

β oraz β ׀−

ℜ

γ. Istnieją zatem odpowiednie dowody wprost lub

nie wprost dla formuł β oraz γ. W przypadku dowodów wprost istnieje ciąg
dowodowy α

1

, α

2

, ..., α

n

taki, że α

n

= β i każda formuła ciągu jest formułą α lub

wynika z poprzednich formuł ciągu w myśl reguł ze zbioru ℜ, oraz istnieje ciąg
dowodowy β

1

, β

2

, ..., β

m

taki, że β

m

= γ i każda formuła ciągu jest formułą β lub

wynika z poprzednich formuł ciągu w myśl reguł ze zbioru ℜ. Jeżeli rozważymy
ciąg α

1

, α

2

, ..., α

n

, β

1

, β

2

, ..., β

m

, można zauważyć, że spełnia on warunki dla ciągu

dowodowego wprost dla formuły γ na gruncie formuły α oraz układu reguł ℜ.
W innych przypadkach dowód jest analogiczny.

Powyższe twierdzenie można uogólnić w następujący sposób:

Twierdzenie 6

Dla dowolnego zbioru formuł X = {α

1

, α

2

, ..., α

n

} oraz dla dowolnych

formuł β, γ i dowolnego niepustego układu reguł ℜ, jeżeli α

1

, α

2

, ..., α

n

׀−

ℜ

β

oraz α

1

, α

2

, ..., α

n

, β ׀−

ℜ

γ, to spełnione jest również α

1

, α

2

, ..., α

n

׀−

ℜ

γ.

9

Dowód

Załóżmy, że

α

1

, α

2

, ..., α

n

׀−

ℜ

β. Istnieje zatem odpowiedni dowód wprost lub

nie wprost dla formuły β. W przypadku dowodu wprost istnieje ciąg dowodowy

β

1

, β

2

, ..., β

n

taki, że β

n

= β i każda formuła ciągu jest formułą ze zbioru

X = {α

1

, α

2

, ..., α

n

} lub wynika z poprzednich formuł ciągu w myśl reguł ze zbioru

ℜ. Załóżmy także, że α

1

, α

2

, ..., α

n

, β ׀−

ℜ

γ, istnieje zatem odpowiedni dowód

wprost lub nie wprost dla formuły γ. W przypadku dowodu wprost istnieje ciąg
dowodowy γ

1

, γ

2

, ..., γ

n

taki, że γ

n

= γ i każda formuła ciągu jest formułą ze zbioru

{α

1

, α

2

, ..., α

n

, β} lub wynika z poprzednich formuł ciągu w myśl reguł ze zbioru ℜ.

Rozważmy ciąg skonstruowany w sposób następujący: Jeżeli w ciągu dowodowym

γ

1

, γ

2

, ..., γ

n

któraś z formuł jest formułą β, to formułę tę zastępujemy ciągiem

dowodowym β

1

, β

2

, ..., β

n

. Skonstruowany w ten sposób ciąg dowodowy jest ciągiem

dowodowym dla formuły γ na gruncie formuł ze zbioru X = {α

1

, α

2

, ..., α

n

}. Mamy

zatem α

1

, α

2

, ..., α

n

׀−

ℜ

γ. W pozostałych przypadkach dowód jest analogiczny.

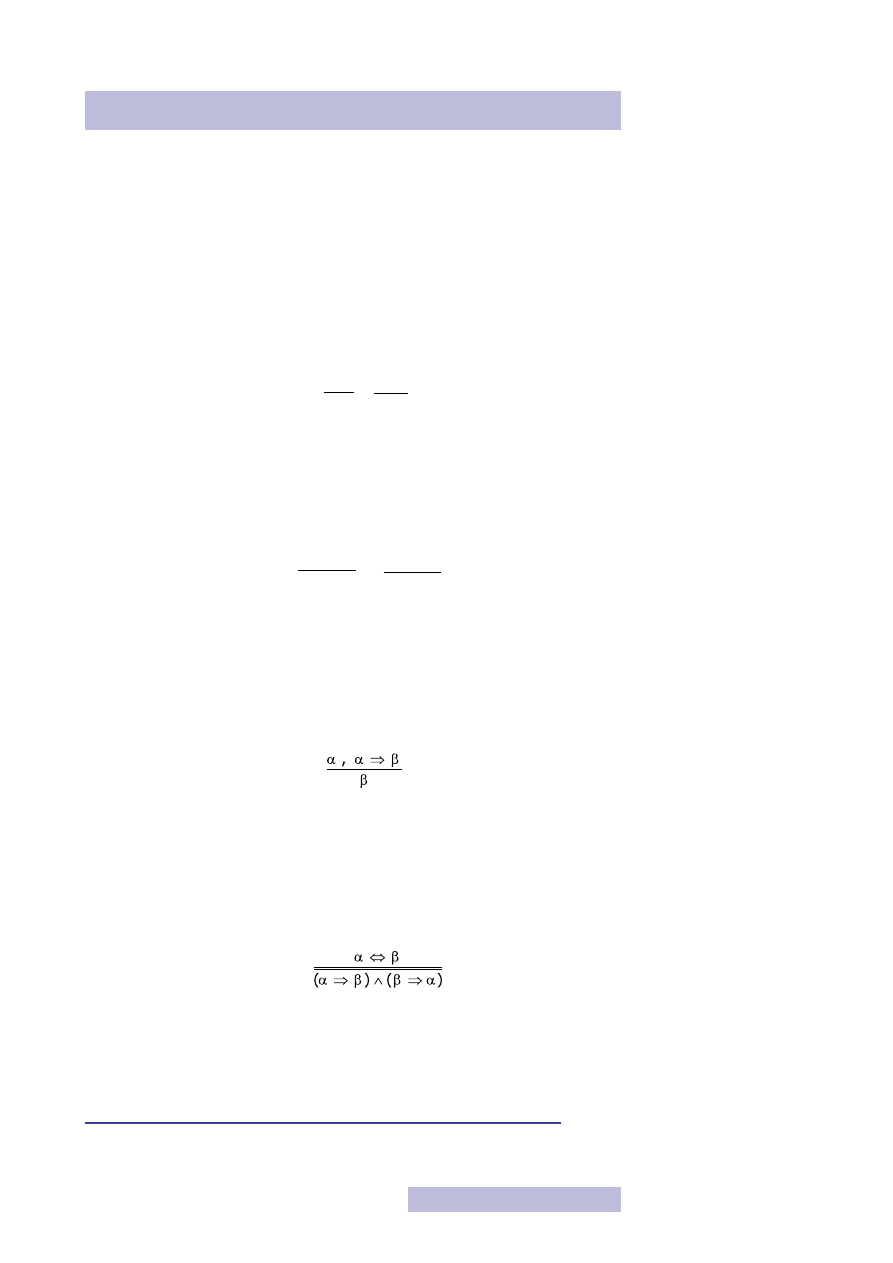
10

3. System dedukcji naturalnej

Przedstawimy teraz układ reguł umożliwiających przeprowadzanie dowodów,
nazywany układem dedukcji naturalnej

1

.

Reguły dedukcji naturalnej

Reguły

E

liminacji

K

oniunkcji:

EK

:

α

∧

β

α

,

α

∧

β

β

Jeżeli w ciągu dowodowym mamy jako przesłankę koniunkcję, to możemy do
dowodu dopisać każdy czynnik koniunkcji.

Reguły

E

liminacji

A

lternatywy:

EA

:

α

∨

β,

¬

α

β

,

α

∨

β,

¬

β

α

Jeżeli w ciągu dowodowym mamy jako przesłanki alternatywę i negację jednego
z jej składników, to możemy do dowodu dopisać drugi składnik alternatywy.

Reguła

E

liminacji

I

mplikacji:

EI

:

Jeżeli w ciągu dowodowym mamy jako przesłanki pewną formułę i implikację
o takim samym poprzedniku, to możemy do dowodu dopisać następnik tej
implikacji.

R

eguły

R

ównoważności:

RR :

Jeżeli w ciągu dowodowym mamy jako przesłankę równoważność dwóch formuł,
to możemy dopisać do ciągu dowodowego koniunkcję odpowiednich implikacji.
Zachodzi również reguła odwrotna.

1

Prezentowany układ jest pewnym rozszerzeniem systemu zaproponowanego i przebadane-

go przez polskich logików Ludwika Borkowskiego i Jerzego Słupeckiego.

11

Reguła

D

ołączania

K

oniunkcji:

DK

:

Do ciągu dowodowego zawsze możemy dopisać koniunkcję dowolnych przesłanek
występujących w ciągu dowodowym.

Reguły

D

ołączania

A

lternatywy:

DA

:

Do ciągu dowodowego zawsze możemy dopisać alternatywę którejkolwiek
z przesłanek występujących w ciągu dowodowym z dowolną formułą.

Reguła

D

ołączania

I

mplikacji (z negacji

P

oprzednika):

DIP

:

Jeżeli w ciągu dowodowym mamy jako przesłankę negację pewnej formuły, to
możemy do dowodu dopisać implikację o poprzedniku będącym tą formułą
i dowolnym następniku.

Reguła

D

ołączania

I

mplikacji (z

N

astępnika):

DIN

:

Jeżeli w ciągu dowodowym mamy jako przesłankę pewną formułę, to możemy do
dowodu dopisać implikację o dowolnym poprzedniku i następniku będącym tą
formułą.

Reguły

P

odwójnej

N

egacji:

PN

:

.

Jeżeli w ciągu dowodowym mamy jako przesłankę negację negacji pewnej formuły, to
możemy do dowodu dopisać tę formułę. I odwrotnie — jeżeli w ciągu dowodowym
mamy jako przesłankę pewną formułę, to możemy do dowodu dopisać negację
negacji tej formuły.

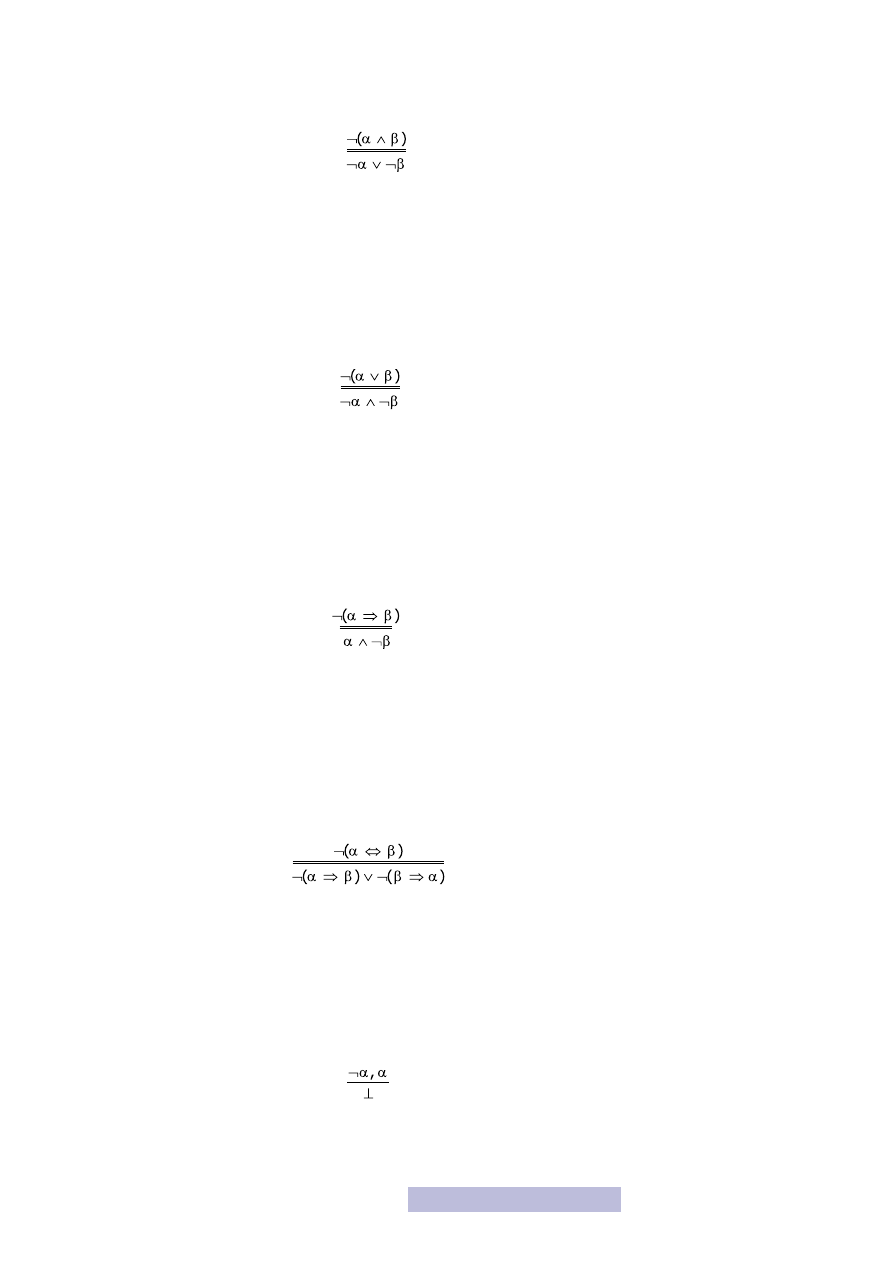
12

Reguły

N

egacji

K

oniunkcji:

NK

:

Jeżeli w ciągu dowodowym mamy jako przesłankę negację koniunkcji dwóch
formuł, to możemy do dowodu dopisać alternatywę negacji tych formuł. Jeżeli
w ciągu dowodowym mamy alternatywę negacji dwóch formuł, to możemy dopisać
do dowodu negację ich koniunkcji.

Reguły

N

egacji

A

lternatywy:

NA

:

Jeżeli w ciągu dowodowym mamy jako przesłankę negację alternatywy dwóch
formuł, to możemy do dowodu dopisać koniunkcję negacji tych formuł. Jeżeli
w ciągu dowodowym mamy koniunkcję negacji dwóch formuł, to możemy dopisać
do dowodu negację ich alternatywy.

Reguły

N

egacji

I

mplikacji:

NI

:

Jeżeli w ciągu dowodowym mamy jako przesłankę negację implikacji, to możemy
do dowodu dopisać koniunkcję poprzednika tej implikacji i negacji jej następnika.
Jeżeli w ciągu dowodowym mamy koniunkcję formuły i negacji innej formuły, to
możemy do dowodu dopisać negację implikacji tych formuł.

Reguły

N

egacji

R

ównoważności:

NR

:

Jeżeli w ciągu dowodowym mamy jako przesłankę negację równoważności
dwóch formuł, to możemy dopisać do ciągu dowodowego alternatywę negacji
odpowiednich implikacji. Zachodzi również reguła odwrotna.

Reguła

D

ołączania

S

przeczności:

DS

:

13

Jeżeli w ciągu dowodowym mamy jako przesłanki formułę i jej negację, to możemy
do dowodu dopisać symbol sprzeczności.

Wynikanie syntaktyczne na gruncie powyższego układu reguł będziemy oznaczać
symbolem ׀−

DN

.

Przykład 10

Wykażemy, że:

p ∧ ¬q, p ⇒ s, t ∨ q ׀−

DN

s ∧ t.

Wypisujemy kolejno założenia — (Z):
1. ϕ

1

= p ∧ ¬q (Z).

2. ϕ

2

= p ⇒ s (Z).

3. ϕ

3

= t ∨ q (Z).

Formuły ϕ

4

oraz ϕ

5

wyprowadzamy z formuły ϕ

1

(założenia 1) w myśl reguły

EK

:

4. ϕ

4

= p (1,

EK

).

5. ϕ

5

= ¬q (1,

EK),

Kolejno stosujemy do odpowiednich formuł reguły

EI

,

EA

oraz

DK

:

6. ϕ

6

= s (2, 4

EI

).

7. ϕ

7

= t (3, 5,

EA

).

8. ϕ

8

= s ∧ t (6, 7,

DK

).

Zauważmy, że — podobnie jak w poprzednim przykładzie — każda formuła
powyższego ciągu jest albo elementem zbioru X, albo wnioskiem z wcześniejszych
formuł ciągu w myśl pewnej reguły dedukcji naturalnej. Możemy zatem stwierdzić,
że p ∧ ¬q, p ⇒ s, t ∨ q ׀−

DN

s ∧ t.

Przykład 11

Wykażemy, że:

p ∨ q, ¬(s ⇒ q), s ⇒ t ׀−

DN

s ⇒ (p ∧ t).

Wypisujemy kolejno założenia — (Z):

1. ϕ

1

= p ∨ q (Z).

2. ϕ

2

= ¬(s ⇒ q) (Z).

3. ϕ

3

= s ⇒ t (Z).

Korzystamy z reguły negacji implikacji

NI

:

4. ϕ

4

= s ∧ ¬q (2,

NI).

Formuły

ϕ

5

oraz ϕ

6

wyprowadzamy z formuły ϕ

4

w myśl reguły

EK

:

5. ϕ

5

= s (4,

EK

).

6. ϕ

6

= ¬q (4,

EK).

Kolejno stosujemy do odpowiednich formuł reguły

EA

,

EI

,

DK

oraz

DIN

:

7. ϕ

7

= p (1, 6,

EA

).

8. ϕ

8

= t (3, 5,

EI

).

9. ϕ

9

= p ∧ t (7, 8,

DK

).

10. ϕ

10

= s ⇒ (p ∧ t) (9,

DIN).

Zauważmy, że — podobnie jak w poprzednim przykładzie — każda formuła
powyższego ciągu jest albo elementem zbioru X (założenia), albo wnioskiem
z wcześniejszych formuł ciągu w myśl pewnej reguły dedukcji naturalnej. Możemy
zatem stwierdzić, że p ∨ q, ¬(s ⇒ q), s ⇒ t ׀−

DN

s ⇒ (p ∧ t).

14

Przykład 12

Udowodnimy metodą nie wprost wynikanie:

p ׀−

DN

p ∨ q.

Wypisujemy założenie — (Z):
1.

p (Z),

a następnie dopisujemy negację wniosku (oznaczamy to symbolem ZN):
2. ¬(p ∨ q) (ZN).
Stosując do punktu 2 regułę negacji alternatywy, otrzymujemy:
3. ¬p ∧ ¬q (2,

NA

).

4. ¬p (3,

EK).

5.

⊥ (1, 4,

DS

).

Przykład 13

Udowodnimy również metodą nie wprost dowodzone wyżej wynikanie:

p ∨ q, ¬(s ⇒ q), s ⇒ t ׀−

DN

s ⇒ (p ∧ t).

Wypisujemy kolejno założenia — (Z):

1. p ∨ q (Z).
2. ¬(s ⇒ q) (Z).
3. s ⇒ t (Z),

a następnie dopisujemy negację wniosku (oznaczamy to symbolem ZN).

4. ¬[s ⇒ (p ∧ t)] (ZN).

Kolejno stosując do odpowiednich formuł reguły dedukcji naturalnej, uzyskujemy
następujące formuły:

5. s ∧ ¬(p ∧ t) (4,

NI

),

6. s (5,

EK

),

7. ¬(p ∧ t) (5,

EK

),

8. ¬p ∨ ¬t (7,

NK

),

9. t (3, 6,

EI

),

10. s ∧ ¬q (2,

NI

),

11. ¬q (10,

EK

),

12. p (1, 11,

EA

),

13. ¬¬t (9,

PN

),

14. ¬p (8, 13,

EA

),

15. ⊥ (w punktach 12 i 14), co kończy dowód.
Dla podanego wyżej systemu dedukcji naturalnej zachodzi następujące:

Twierdzenie 7

(mocne twierdzenie o pełności względem semantyki rachunku zdań)

Formuła

α wynika syntaktycznie ze zbioru formuł X na gruncie systemu

DN

(X ׀−

DN

α) wtedy i tylko wtedy, gdy formuła α wynika semantycznie ze zbioru

formuł X (X ׀= α).

Symbolicznie:

X ׀−

DN

α wtedy i tylko wtedy, gdy X ׀= α.

Powróćmy do metody dowodzenia nie wprost. Możliwość dopisania negacji
dowodzonej formuły do przesłanek umożliwia dowodzenie formuł bez przesłanek.
Takie bezprzesłankowe wynikania oznaczać będziemy ׀−

DN

α (bez wypisywania

przesłanek przed znakiem wynikania), a o formułach mających dowody bez
przesłanek będziemy mówić, że

wynikają z systemu

dedukcji naturalnej DN.

15

Przykład 14

Udowodnimy metodą nie wprost poniższe wynikanie:

׀−

DN

¬p ⇒ (p ⇒ q).

Negację dowodzonej formuły umieszczamy w dowodzie jako założenie nie wprost
— (ZN):
1. ¬(¬p ⇒ (p ⇒ q)) (ZN).
Kolejno stosując do odpowiednich formuł reguły dedukcji naturalnej uzyskujemy
następujące formuły:
2. ¬p ∧ ¬(p ⇒ q) (1,

NI

).

3. ¬p (2,

EK

).

4. ¬(p ⇒ q) (2,

EK

).

5. p

∧ ¬q (4,

NI

).

6. p (5,

EK).

7.

⊥ (3, 6

DS).

Dla formuł mających dowody bez przesłanek zachodzi następujące:

Twierdzenie 8

(słabe twierdzenie o pełności względem semantyki rachunku zdań)

Formuła

α wynika syntaktycznie z systemu

DN

(׀−

DN

α) wtedy i tylko wtedy, gdy

formuła α wynika semantycznie ze zbioru pustego (׀= α).

Symbolicznie:

׀−

DN

α wtedy i tylko wtedy, gdy ׀= α.

16

4. Dowody przez dodatkowe założenie

Omówione w poprzednich paragrafach techniki dowodowe można wzbogacić
jeszcze o następującą metodę. Jeżeli dowodzonym wnioskiem jest formuła będąca
implikacją, to poprzednik tej implikacji możemy dołączyć do założeń dowodu.
Wnioskiem pozostaje następnik tej implikacji. Dalsze postępowanie podczas
dowodzenia opiera się na wcześniej omówionych technikach dowodu wprost
i dowodu nie wprost. Wynikania dowodzone za pomocą tej metody będziemy
oznaczać symbolem

׀−

DNZ

.

Przykład 15

Udowodnimy wprowadzoną wyżej metodą następujące wynikanie:

p ⇒ q, q ⇒ r ׀−

DNZ

p ⇒ r.

Wypisujemy kolejno założenia — (Z):
1. p ⇒ q (Z).
2. q ⇒ r (Z),
a następnie dopisujemy poprzednik wniosku (oznaczamy to symbolem ZD):
3. p (ZD).
Kolejno stosując do odpowiednich formuł reguły dedukcji naturalnej, uzyskujemy
następujące formuły:
4. q (1, 3

EI

).

5. r (2, 4

EI

).

Co kończy dowód, mamy zatem p ⇒ q, q ⇒ r ׀−

DNZ

p ⇒ r.

Przykład 16

Udowodnimy wynikanie ׀−

DNZ

(p ⇒ r) ⇒ [(q ⇒ r) ⇒ (p ∧ q ⇒ r)].

Wypisujemy kolejno założenia dodatkowe — (ZD) (po dopisaniu poprzednika
implikacji jako dodatkowego założenia, zauważamy, że następnik jest również
implikacją, zatem można dopisać jako założenie dodatkowe jej poprzednik itp.).
1. p ⇒ r (ZD).
2. q ⇒ r (ZD).
3. p ∧ q (ZD).
Kolejno stosując do odpowiednich formuł reguły dedukcji naturalnej, uzyskujemy
następujące formuły:
4. p (3,

EK

).

5. r (1, 4

EI).

Co kończy dowód, mamy zatem

׀−

DNZ

(p ⇒ r) ⇒ [(q ⇒ r) ⇒ (p ∧ q ⇒ r)].

17

5. Formy zdaniowe

Rachunek zdań jest najprostszym i najbardziej rozpowszechnionym rachunkiem
logicznym. Niestety, z różnych powodów nie wystarcza do opisu rzeczywistości.
Przypomnijmy, że rachunek ten bazuje na pojęciu zdania w sensie logicznym, czyli
wyrażenia, któremu jesteśmy w stanie przyporządkować prawdę lub fałsz.

Oczywiście, jeżeli rozważymy wyrażenie „Janek lubi Zosię”, łatwo można
stwierdzić, że jest to zdanie w sensie logicznym. Jednak już drobna modyfikacja
tego wyrażenia — „Człowiek lubi Zosię” — nastręcza problem, jeżeli chodzi
o zaklasyfikowanie go do zbioru zdań. Nie jesteśmy bowiem w stanie orzec, czy to
wyrażenie jest prawdziwe, czy fałszywe.

Podobnie jest w przypadku znanych nam wyrażeń arytmetycznych: 2 + 3 = 6 jest
zdaniem (fałszywym), zaś wyrażenia x + 3 = 6 nie można nazwać zdaniem.

Zauważmy następujące prawidłowości:

 jeżeli w wyrażeniu „Człowiek lubi Zosię” wyraz „człowiek” zastąpimy imieniem

konkretnej osoby, to uzyskamy zdanie (np. „Janek lubi Zosię”),

 jeżeli w wyrażeniu x + 3 = 6 zastąpimy zmienną x konkretną wartością

dowolnej liczby, to uzyskamy zdanie (np. 2 + 3 = 6).

Forma zdaniowa zmiennej

x to wyrażenie, które zawiera tę zmienną i które staje się

zdaniem po wstawieniu za zmienną pewnych obiektów.

Zakres

danej

formy

to dowolny zbiór takich elementów, które wstawione do formy

w miejsce zmiennej dają wyrażenia sensowne.

Przykład 17

Oczywiście wyrażenie „Człowiek lubi Zosię” jest formą zdaniową zmiennej
„człowiek”. Zakresem tej formy może być dowolny zbiór ludzi.

Przykład 18

Wyrażenia x + 3 = 6, x + 1 = 4 czy x + 3 ≥ 6 są formami zdaniowymi zmiennej
x. Zakresem tej formy może być dowolny zbiór liczbowy.

W dalszych rozważaniach formy zdaniowe zmiennej x będziemy oznaczali
symbolami ϕ(x), ψ(x) itp. Zauważmy również, że jeżeli za zmienną w formie ϕ(x)
podstawimy element zakresu a, to wyrażenie ϕ(a) jest zdaniem w sensie logicznym
i jako takie może przyjmować wartości 0 lub 1.

Przykład 19

Rozważmy formę zdaniową ϕ(x) : (x + 3 = 6) oraz zakres {0, 1, 2, 3, 4, 5}.
Zauważmy, że wyrażenie ϕ(1) : (1 + 3 = 6) jest zdaniem fałszywym, co możemy
zapisać w(ϕ(1)) = 0, zaś wyrażenie ϕ(3) : (3 + 3 = 6) jest zdaniem prawdziwym,
co możemy zapisać w(ϕ(3)) = 1.

Formy zdaniowe możemy łączyć spójnikami logicznymi, budując formy złożone.
Jeżeli ϕ(x) i ψ(x) są formami zdaniowymi, to wyrażenia: ¬ϕ(x), ¬ψ(x), ϕ(x) ∧ ψ(x),

18

ϕ(x) ∨ ψ(x), ϕ(x) ⇒ ψ(x), ϕ(x) ⇔ ψ(x) są również formami zdaniowymi. Formy:

ϕ(x) ∧ ψ(x), ϕ(x) ∨ ψ(x), ϕ(x) ⇒ ψ(x), ϕ(x) ⇔ ψ(x) możemy również oznaczać
odpowiednio w sposób następujący: (ϕ ∧ ψ)(x), (ϕ ∨ ψ)(x), (ϕ ⇒ ψ)(x), (ϕ ⇔ ψ)(x),
akcentując w ten sposób, że zmienne form składowych są takie same.

Niech ϕ(x) będzie formą zdaniową zmiennej x, zaś zbiór X będzie jej zakresem.

Powiemy, że

element

a należący do zbioru X

spełnia formę zdaniową

ϕ(x) wtedy

i tylko wtedy, gdy po wstawieniu w miejsce zmiennej x w formie ϕ(x) elementu
a otrzymamy zdanie prawdziwe — czyli w(ϕ(a)) = 1.

Analogicznie powiemy, że

element

a należący do zbioru X

nie spełnia formy zdaniowej

ϕ(x) wtedy i tylko wtedy, gdy po wstawieniu w miejsce zmiennej x w formie ϕ(x)
elementu a, otrzymamy zdanie fałszywe — czyli w(ϕ(a)) = 0.

W zależności od rozpatrywanego zakresu, formy można podzielić na trzy
kategorie:
1. Formę ϕ(x) nazywamy

spełnialną dla danego zakresu

, jeżeli

istnieje

element zakresu

a spełniający tę formę (w(ϕ(a)) = 1).

2. Formę ϕ(x) nazywamy

prawdziwą dla danego zakresu

, jeżeli

każdy

element tego

zakresu a spełnia tę formę (w(ϕ(a)) = 1).

3. Formę ϕ(x) nazywamy

fałszywą dla danego zakresu

, jeżeli żaden element tego

zakresu a nie spełnia formy (w(ϕ(a)) = 0).

Przykład 20

Rozważmy jako przykład następujące formy ϕ

1

(x) : (x = x), ϕ

2

(x) : (2x = 4) oraz

ϕ

3

(x) : (x > x) w zakresie liczb rzeczywistych R.

Zauważmy, że:

 podstawienie dowolnej liczby rzeczywistej do formy ϕ

1

(x) daje zdanie

prawdziwe,

 istnieje liczba rzeczywista, która po podstawieniu za zmienną x w formie ϕ

2

(x)

daje zdanie prawdziwe, mamy bowiem w(ϕ

2

(2)) = 1,

 żadna liczba rzeczywista podstawiona do formy ϕ

3

(x) nie daje zdania

prawdziwego.

Oczywiście, zgodnie z podanymi wcześniej definicjami można stwierdzić, że

ϕ

1

(x) jest formą prawdziwą, ϕ

2

(x) — spełnialną oraz ϕ

3

(x) — formą fałszywą

w zakresie liczb rzeczywistych R.

Przykład 21

Zauważmy, że pojęcia spełnialności, prawdziwości i fałszywości form zdaniowych
są ściśle związane z rozpatrywanym zakresem. Rozważmy bowiem formę

ϕ(x) : (x ≥ 4) w trzech różnych zakresach, będących przedziałami prostej
rzeczywistej. W przedziale (−∞, 2) forma ϕ(x) jest formą fałszywą, w przedziale
(0, +∞) — spełnialną, zaś w przedziale (4, +∞) — prawdziwą.

19

6. Kwantyfikatory

Rozważaliśmy w poprzednim paragrafie wyrażenia typu „Człowiek lubi Zosię”
lub x + 3 = 6, o których orzekliśmy, że nie są zdaniami w sensie logicznym.
Stwierdziliśmy, że aby nadać tym wyrażeniom sens zdania, należy podstawić
w miejsce zmiennej jakiś obiekt.

Rozważmy teraz następujące modyfikacje tych wyrażeń: „Każdy człowiek lubi
Zosię” oraz „Istnieje liczba x taka, że x + 3 = 6”. Zauważmy, że wyrażenia te są
już zdaniami w sensie logicznym.

Zauważmy, że zwrot „Istnieje takie x, że...” można uważać za równoważny zwrotowi:
„Dla pewnego x jest ...”. Zwrot ten nazywamy

kwantyfikatorem egzystencjalnym

(lub

małym

albo

szczegółowym

) i oznaczamy symbolem ∃

x

.

Zauważmy, że wyrażenie ∃

x

ϕ(x) jest zdaniem w sensie logicznym.

Zwrot „dla każdego” nazywamy

kwantyfikatorem uniwersalnym

(

ogólnym

lub

dużym

)

i oznaczamy symbolem ∀

x

. Zauważmy, że wyrażenie ∀

x

ϕ(x) jest zdaniem w sensie

logicznym.

Zmienna występująca w zasięgu (wyznaczanym zwyczajowo przez odpowiedni
nawias) kwantyfikatora identyczna z kwantyfikowaną kwantyfikatorem zmienną
nazywa się zmienną związaną danym kwantyfikatorem. Natomiast zmienna
występująca w wyrażeniu, która nie jest związana żadnym kwantyfikatorem,
nazywa się zmienną wolną.

Jeżeli w zasięgu kwantyfikatora znajdują się jakieś inne kwantyfikatory, to
kwantyfikator początkowy wiąże tylko te zmienne, które nie są związane żadnym
kwantyfikatorem zawartym w jego zasięgu.

Przykład 22

Rozważmy następujące wyrażenie ∀

x

(2x + y = 5). Zasięgiem kwantyfikatora jest

wyrażenie 2x + y = 5. Zmienna x jest w tym wyrażeniu zmienną związaną, zaś
zmienna y zmienną wolną.

Podamy teraz definicję

formuł (wyrażeń) kwantyfikatorowych

.

Poprawnie zbudowanymi wyrażeniami (formułami) kwantyfikatorowymi
są wszystkie zmienne zdaniowe p, q, ... oraz wszystkie symbole form zdaniowych

ϕ(x), ψ(x), .....

Jeżeli α i β są poprawnie zbudowanymi formułami kwantyfikatorowymi, to ¬α,

¬

β, α ∧ β, α ∨ β, α ⇒ β, α ⇔ β są również poprawnie zbudowanymi formułami

kwantyfikatorowymi.

Jeżeli α jest poprawnie zbudowaną formułą kwantyfikatorową, w której x nie
jest zmienną związaną, to ∀

x

α oraz ∃

x

α są również poprawnie zbudowanymi

wyrażeniami kwantyfikatorowymi.

Poprawnie zbudowane wyrażenie kwantyfikatorowe, w którym nie występują
zmienne wolne, nazywamy

zdaniem rachunku kwantyfikatorów.

20

Wyrażenie matematyczne

jest podstawieniem poprawnie zbudowanego wyrażenia

kwantyfikatorowego wtedy i tylko wtedy, gdy powstaje z niego przez zastąpienie
wszystkich zmiennych zdaniowych p, q, ... zdaniami w sensie logicznym,
a wszystkich wyrażeń typu ϕ(x) — formami zdaniowymi.

Poprawnie zbudowane wyrażenie kwantyfikatorowe jest

prawem rachunku

kwantyfikatorów

(

tautologią kwantyfikatorową

) wtedy i tylko wtedy, gdy każde

poprawne podstawienie tego wyrażenia jest prawdziwym zdaniem matematycznym
lub prawdziwą formą zdaniową.

Twierdzenie 9

Wszystkie prawa rachunku zdań są prawami rachunku kwantyfikatorów.

Twierdzenie 10

Prawami rachunku kwantyfikatorów są następujące wyrażenia (w nawiasach
podajemy pewne ich podstawienia):
(a) ∀

x

ϕ(x) ⇒ ∃

x

ϕ(x)

[∀

x

(x + 1 = 2) ⇒ ∃

x

(x +1 = 2) lub ∀

x

(x

2

≥ 0) ⇒ ∃

x

(x

2

≥ 0)],

(b) ∀

x

ϕ(x) ⇒ ϕ(a)

[∀

x

(x

2

≥ 0) ⇒ (4

2

≥ 0) lub ∀

x

(–x

2

< 0) ⇒ (–3

2

< 0)],

(c) ϕ(a) ⇒ ∃

x

ϕ(x)

[(2 + 1 = 3) ⇒ ∃

x

(x + 1 = 3) lub (1 < 3) ⇒ ∃

x

(x < 3)].

Twierdzenie 11

Jeżeli x nie jest zmienną wolną formy ϕ, to następujące wyrażenia są prawami
rachunku kwantyfikatorów:
(a) ∀

x

(ϕ ∨ ψ(x)) ⇔ (ϕ ∨ ∀

x

ψ(x)),

(b) ∀

x

(ϕ ∧ ψ(x)) ⇔ (ϕ ∧ ∀

x

ψ(x)),

(c) ∀

x

(ϕ ⇒ ψ(x) ⇔ (ϕ ⇒ ∀

x

ψ(x)),

(d) ∃

x

(ϕ ∨ ψ(x)) ⇔ (ϕ ∨ ∃

x

ψ(x)),

(e) ∃

x

(ϕ ∧ ψ(x)) ⇔ (ϕ ∧ ∃

x

ψ(x)),

(f) ∃

x

(ϕ ⇒ ψ(x) ⇔ (ϕ ⇒ ∃

x

ψ(x).

Twierdzenie 12

Prawami rachunku kwantyfikatorów są następujące wyrażenia:
(a) ¬∀

x

ϕ(x) ⇔ ∃

x

¬

ϕ(x) — prawo de Morgana rachunku kwantyfikatorów,

(b) ¬∃

x

ϕ(x) ⇔ ∀

x

¬

ϕ(x) — prawo de Morgana rachunku kwantyfikatorów,

(c) ∀

x

[ϕ(x) ∧ ψ(x)] ⇔ [∀

x

ϕ(x) ∧ ∀

x

ψ(x)] — prawo dystrybucji kwantyfikatora

uniwersalnego względem koniunkcji,

(d) ∃

x

[ϕ(x) ∨ ψ(x)] ⇔ [ ∃

x

ϕ(x) ∨ ∃

x

ψ(x)] — prawo dystrybucji kwantyfikatora

egzystencjalnego względem alternat yw y,

(e) [∀

x

ϕ(x) ∨ ∀

x

ψ(x)] ⇒ ∀

x

[ϕ(x) ∨ ψ(x)] — prawo dystrybucji kwant yfikatora

uniwersalnego względem alternat yw y,

(f) ∃

x

[ϕ(x) ∧ ψ(x)] ⇒ [∃

x

ϕ(x) ∧ ∃

x

ψ(x)]

— prawo dystrybucji kwant yfikatora

egzystencjalnego względem koniunkcji,

(g) ∀

x

[ϕ(x) ⇒ ψ(x)] ⇒ [∀

x

ϕ(x) ⇒ ∀

x

ψ(x)] — prawo dystrybucji kwantyfikatora

uniwersalnego względem implikacji,

21

(h) ∀

x

[ϕ(x) ⇒ ψ(x)] ⇒ [∃

x

ϕ(x) ⇒ ∃

x

ψ(x)] — prawo dystrybucji kwantyfikatora

egzystencjalnego względem implikacji.

Twierdzenie 13

Następujące wyrażenia nie są prawami rachunku kwantyfikatorów:
(a) ∃

x

ϕ(x) ∧ ∃

x

ψ(x) ⇒ ∃

x

[ϕ(x) ∧ ψ(x)],

(b) ∀

x

[ϕ(x) ∨ ψ(x)] ⇒ [∀

x

ϕ(x) ∨ ∀

x

ψ(x)].

Dowód

(a) rozważmy

podstawienie

∃

x

(x = 1) ∧ ∃

x

(x = 2) ⇒ ∃

x

[(x = 1) ∧ (x = 2)]

w zakresie liczb rzeczywistych R. Oczywiście poprzednik tej implikacji jest
prawdziwy (istnieje liczba rzeczywista równa jeden i istnieje liczba rzeczywista
równa 2), ale następnik jest fałszywy (nie istnieje liczba rzeczywista równa
jednocześnie jeden i dwa). Zatem implikacja jest fałszywa. Zgodnie z definicją
wyrażenie nie jest prawem rachunku kwantyfikatorów;

(b) rozważmy

podstawienie

∀

x

[(x ≥ 0) ∨ (x ≤ 0)] ⇒ [∀

x

(x ≥ 0) ∨ ∀

x

(x ≤ 0)]

w zakresie liczb rzeczywistych R. Poprzednik tej implikacji jest prawdziwy
(prawdą jest, że dowolna liczba rzeczywista jest mniejsza lub równa od zera
lub większa lub równa od zera), ale następnik jest fałszywy (nieprawdą jest, że
każda liczba rzeczywista jest nieujemna lub to, że każda liczba rzeczywista jest
niedodatnia). Implikacja jest fałszywa i zgodnie z definicją wyrażenie nie jest
prawem rachunku kwantyfikatorów.

Twierdzenie 14

Prawami rachunku kwantyfikatorów są następujące wyrażenia:
(a) ∀

x

∀

y

ϕ(x, y) ⇔ ∀

y

∀

x

ϕ(x, y),

(b) ∃

x

∃

y

ϕ(x, y) ⇔ ∃

y

∃

x

ϕ(x, y),

(c) ∃

x

∀

y

ϕ(x, y) ⇒ ∀

y

∃

x

ϕ(x, y),

ale nie jest prawem wyrażenie:
(d) ∀

x

∃

y

ϕ(x, y) ⇒ ∃

y

∀

x

ϕ(x, y).

Dowód (d)

Rozważmy podstawienie ∀

x

∃

y

(y < x) ⇒ ∃

y

∀

x

(y < x) w zakresie liczb rzeczywistych

R. Poprzednik implikacji jest prawdziwy: dla dowolnej liczby rzeczywistej istnieje
liczba od niej mniejsza. Następnik jest fałszywy: nie ma bowiem liczby rzeczywistej,
od której byłyby większe wszystkie liczby rzeczywiste.

22

Bibliografia

1.

Gubareni N., 2001: Logika dla studentów, Wydawnictwo Politechniki

Częstochowskiej.

2.

Kuratowski K., 2004: Wstęp do teorii mnogości i topologii, PWN,

Warszawa.

3.

Marek W., Onyszkiewicz J., 2003: Elementy logiki i teorii mnogości

w zadaniach, PWN, Warszawa.

4.

Rasiowa H., 2004: Wstęp do matematyki współczesnej, PWN,

Warszawa.

5.

Słupecki J., Hałkowska K., Piróg-Rzepecka K., 1994: Logika i teoria

mnogości

, Warszawa.

Bibliografia stron WWW

6. Wydział Matematyki, Informatyki i Mechaniki Uniwersytetu Warszawskiego.

Witryna internetowa. h�p://www.mimuw.edu.pl/~tiuryn/skrypt-98.ps.gz, stan

z 21.09.2005 (J. Tiuryn, Wstęp do teorii mnogości i logiki).