Spis zagadnień egzaminacyjnych z przedmiotu:

Algebra z geometrią. Część II

Automatyka i Robotyka.

27. Pierścienie, pierścienie wielomianów, pierścienie Z

n

, homomorfizm pierścieni.

28. Ciała, ciało Galois, rozszerzenie ciała, ciało ułamków nad pierścieniem.

29. Określić przestrzeń liniową i podać przykłady przestrzeni liniowej.
30. Liniowa zależność i liniowa niezależność wektorów.
31. Powłoka liniowa układu wektorów.

32. Wymiar przestrzeni liniowej i jej baza.
33. Omów zagadnienie przejścia z bazy do bazy przestrzeni liniowej.
34. Określić odwzorowanie liniowe.
35. Związek odwzorowania liniowego z macierzą.

36. Wektor własny przekształcenia liniowego.
37. Równanie charakterystyczne macierzy i jego pierwiastki – wartości własne macierzy.
38. Podać twierdzenie Ceyleya – Hamiltona (dowód).

39. Określić iloczyn skalarny w przestrzeni liniowej.
40. Macierze podobne. Diagonalizacja macierzy.
41. Określić działania na wektorach w przestrzeni trójwymiarowej.
42. Określić wektor w postaci analitycznej (w układzie kartezjańskim).

43. Podać sposoby wyliczania iloczynu wektorowego wektorów.
44. Warunki równoległości i prostopadłości wektorów.
45. Podać znane postaci równania płaszczyzny. Wyprowadzić równanie parametryczne płaszczyzny.

46. Wyprowadzić wzór na obliczanie odległości punktu od płaszczyzny.
47. Równanie prostej w przestrzeni trójwymiarowej.
48. Wyprowadzić równanie prostej w postaci parametrycznej i kierunkowej.

49. Omówić wzajemne położenie prostych, płaszczyzn oraz prostej i płaszczyzny w przestrzeni

trójwymiarowej

50. Definicja okręgu i jego równanie.
51. Definicja hiperboli i jej równanie.

52. Definicja paraboli i jej równie.
53. Kwadrygi ich klasyfikacja.
54. Podać równanie sfery i elipsoidy. Które z tych powierzchni są obrotowe?

55. Wymień znane paraboloidy i podaj ich równania.
56. Wymień znane hiperboloidy i podaj ich równania.
57. Określić powierzchnię walcową i napisać równania znanych walców.

58. określić powierzchnię stożkową i napisać równania znanych stożków.
59. Podać sposób określenia okręgu w przestrzeni trójwymiarowej.
60. Równania prostych stycznych i normalnych do krzywej.
61. Klasyfikacja punktów osobliwych krzywej.

62. Kąt między krzywiznami, styczność i ortogonalność krzywych.
63. Określić styczność rzędu k.
64. Definicja krzywizny. Wyprowadzić wzór na obliczanie krzywizny linii.

65. Określić środek i promień krzywizny.
66. Podać związek między krzywizną i promieniem krzywizny.
67. Wyprowadź równanie koła ściśle stycznego.
68. Omów trójścian Freneta krzywej przestrzennej.

27. Pierścienie, pierścienie wielomianów, pierścienie Z

n

, homomorfizm pierścieni.

Pierścieniem abstrakcyjnym nazywamy algebrę <S,+,

> wyposażoną w relację równości i taką że:

1. <S,+> jest grupą abelową
2. <S,



> jest grupoidem

3. zachodzi rozdzielność działania „•” względem działania „+”.

x,y,z: x(y+z)=(xy)+(xz)

Jeżeli dodatkowo:
x,yS: xy=yx, to pierścień <S,+,



> nazywamy abelowym (przemiennym).

<S,

> jest półgrupą to pierścień <S,+,



> nazywamy łącznym.

<S,

> jest monoidem to pierścień <S,+,



> nazywamy pierścieniem z jednością (unitarnym).

istnieją elementy x,yєS takie, że x≠0, y≠0, ale x•y=0, to x i y nazywamy dzielnikami zera.
Pierścień nie posiadający dzielników zera nazywamy pierścieniem całkowitym.

Pierścień wielomianów jest pierścieniem całkowitym.
Jeśli <S/{0},



> jest półgrupą to pierścień <S,+,



> jest całkowity.

Z[x] - pierścień wielomianów wielomianów o współczynnikach całkowitych
Q[x] - pierścień wielomianów wielomianów o współczynnikach wymiennych
R[x] - pierścień wielomianów wielomianów o współczynnikach rzeczywistych

C[x] - pierścień wielomianów wielomianów o współczynnikach zespolonych

Przykłady pierścieni

Z

n

<Z

4

,+

4

,







+

4

0 1 2 3



4

0 1 2 3

dzielnik zera : 2

0

0 1 2 3

0 0 0 0 0

1

1 2 3 0

1 0 1 2 3

2

2 3 0 1

2 0 2 0 2

3

3 0 1 2

3 0 3 2 1

<Z

5

,+

5

,







+

5

0 1 2 3 4



5

0 1 2 3 4

brak dzielników zera

0

0 1 2 3 4

0 0 0 0 0 0

1

1 2 3 4 0

1 0 1 2 3 4

2

2 3 4 0 1

2 0 2 4 1 3

3

3 4 0 1 2

3 0 3 1 4 2

4

4 0 1 2 3

4 0 4 3 2 1

Homomorfizm pierścieni:

Niech

)

,

,

(

1

0





A

i

)

,

,

(

2

1

a

a

B





będą pierścieniami. Funkcję h: AB nazywamy homomorfizmem pierścienia A w pierścień B, jeśli

spełnia ona warunki:

1. h(a

1

a

2

)=h(a

1

)

h(a

2

)

2. h(a

1

a

2

)=h(a

1

)



h(a

2

)

3. h(0)=e

1

4. h(1)=e

2

28. Ciała, ciało Galois, rozszerzenie ciała, ciało ułamków nad pierścieniem.

Ciałem nazywamy taki pierścień <S,+,



,0,1> w którym <S\{0},







> jest grupą.

Jeżeli w ciele „

” jest przemienne to ciało nazywamy polem.

Niezerowy pierścień utylitarny (z 1) jest ciałem wtedy i tylko wtedy gdy każdy jego element różny od 0 posiada element

odwrotny. Każdy skończony pierścień całkowity jest ciałem.

Ciało Galois – ciało mające skończoną liczbę elementów
Tw. o reprezentacji: Pierścień <Z

n

,+

n

,



n

,0,1> jest ciałem wtedy i tylko wtedy gdy n jest liczbą pierwszą. Takie ciało

nazywamy ciałem Galois GF(n).

Każde ciało skończone jest rozszerzeniem pewnego ciała Galois GF(n), co więcej każde z tych rozszerzeń liczy q=n

m

elementów, gdzie n jest liczbą pierwszą a m





Przykłady ciała Galois:

GF(2)

+

0 1



0 1

0

0 1

0 0 0

1

1 0

1 0 1

GF(4)

+

0 1 A B



0 1 A B

0

0 1 A B

0 0 0 0 0

1

1 0 B A

1 0 1 A B

A A B 0 1

A 0 A B 1

B B A 1 0

B 0 B 1 A

Ciało ułamków nad pierścieniem
Weźmy pierścień <S,+> - jest on łączny, przemienny i bez dzielników zera oraz rozważmy równanie q



x=p gdzie p

S

q

S\{0}. Bez względu czy istnieje rozwiązanie tego równania definiujemy x=(p,q) x=p/q

x

T=S(S\{0}). W zbiorze T definiujemy relację (p,q)~(r,s)ps=qr.

Własności tej relacji:
1. zwrotność (p,q)~(p,q) p

q=qp

2. symetria (p,g)~(r,s)(r,s)~(p,g) p

s=qrrq=sp

3. przechodniość (p,g)~(r,s)

(r,s)~(x,y)(p,g)~(x,y) ps=qr ry=sx psry=qrsx (sr)(py)=(sr)(qx) (p,g)~(x,y)

Definicja ta jest relacją równoważności i dzieli zbiór T na klasy abstrakcji. Każdy element klasy abstrakcji nazywamy ułamkiem

s

q

r

q

s

p

s

r

q

p













s

q

r

p

s

r

q

p









działanie to indukuje działanie w zbiorze T.

Zbiór <T|n,+,

,

1

0

,

1

1

,> jest ciałem. Nazywamy je ciałem ułamków nad pierścieniem i oznaczamy <Fr(S),+,

>.

29. Określić przestrzeń liniową (

wektorową) i podać przykłady przestrzeni liniowej.

Niech będzie dane ciało przemienne <S,+,

,0,1>. Ciało to nazywamy ciałem skalarów (zazwyczaj R lub C) i niech będzie

dany zbiór V, który nie jest zbiorem pustym. W zbiorze V określone są 2 działania:
1.

:(VV)



V

2

. 



(S

V)



V

takie że (własności działań):
1. <V,

,> - jest grupą abelową z elementem neutralnym 

2.



v,s

S





r

V



1



v=r

r



(s



v)=(r



s)



v

3.



r,s

S





u,v

V

(r+s)



v=(r



v)

(s



v)

r



(u

v)=(r



u)

(r



v)

Wówczas system <S,V,

,



,

> nazywamy przestrzenią wektorową nad ciałem S.

Jeżeli v

V to v nazywamy wektorem.

Przykłady przestrzeni wektorowych:
a) macierze np. 3



1 0 0 1

1 1 0 1

0 1 0 0

0 1 0 0

0 1 1 0

0 0 1 0

1 0 1 0

0 0 0 1

1 0 1 1







 

 





 

 





 

 





 

 



1 0 1 1

1 0 1 1

0 0 0 0

1 0 0 1

1 0 0 1

0 0 0 0

1 1 1 1

1 1 1 1

0 0 0 0







 

 





 

 





 

 





 

 



b) ciągi n-elementowe R

n

[x

1

,x

2

,…,x

n

] [y

1

,y

2

,…,y

n

]

c) ciągi nieskończone R



d) dowolne ciało S i V={v}

30. Liniowa zależność i liniowa niezależność wektorów.

Niech będą dane wektory v

1

,v

2

,…,v

n

V i s

1

,s

2

,…,s

n

S.

Sumę







n

i

i

i

v

s

1

nazywamy liniową kombinacją wektorów v

1

,v

2

,…,v

n

.

Jeżeli z równania







n

i

i

i

v

s

1

=

 wynika, że s

1

=s

2

=…=s

n

=0 to o wektorach v

1

,v

2

,…,v

n

mówimy, że są liniowo niezależne.

Jeżeli istnieje układ skalarów s’

1

,s’

2

,…,s’

n

:

s

i

0 , ale







n

i

i

i

v

s

1

=

to v

1

,v

2

,…,v

n

są liczbowo niezależne.

Układ wektorów (v

1

,v

2

,…,v

n

)=U jest liniowo zależny w tedy i tylko w tedy gdy istnieje wektor tego układu, który jest

kombinacją liniową pozostałych wektorów.

31. Powłoka liniowa układu wektorów.

Niech będzie dany układ wektorów U. Zbiór wszystkich kombinacji liniowych wektorów układu U nazywamy powłoką

liniową wektorów tego układu i oznaczamy przez span(u)

lub lin(u).

32. Wymiar przestrzeni liniowej i jej baza.

Bazą przestrzeni liniowej V nazywamy układ liniowo niezależnych wektorów B taki, że span(B)=V. Bazą przestrzeni

wektorowej nazywamy maksymalny układ liniowo niezależnych wektorów tej przestrzeni tzn. taki, że dodanie do tego układu
dowolnego wektora powoduje utratę liniowej niezależności.

W przestrzeni liniowej liczba wektorów bazowych jest stała i nazywamy ją wymiarem tej przestrzeni. |B|=n dim(V)=n.

Jeżeli V jest przestrzenią wektorową i B jest bazą tej przestrzeni, a jej wymiar jest n, tzn. że baza składa się z wektorów
B=( v

1

,v

2

,…,v

n

). Każdy wektor przestrzeni V ma dokładnie jedno przedstawienie w postaci kombinacji liniowej wektorów

bazowych v=







n

i

i

i

v

a

1

. Współczynniki przedstawienia danego wektora w postaci kombinacji liniowej wektorów danej bazy

nazywamy współrzędnymi tego wektora. Liczba współrzędnych jest równa liczbie wektorów bazowych a zatem równa jest

wymiarowi przestrzeni.

Baza standardowa – baza do której można odnosić wszystkie inne bazy.

33. Omów zagadnienie przejścia z bazy do bazy przestrzeni liniowej.

Niech będą dane dwie bazy przestrzeni n-wymiarowej

=(

1

,



2

,…,



n

)

=(

1

,



2

,…,



n

). Każdy wektor



j

z bazy

jest

kombinacją liniową wektorów bazy



j

=







n

i

i

ij

a

1



, j=1,2,…,n. Zatem istnieje macierz przejścia z bazy do bazy -

macierz

kwadratowa stopnia n równa wymiarowi przestrzeni (liczbie wektorów bazowych przestrzeni) umożliwiająca przeliczenie

współrzędnych wektora w jednej bazie na współrzędne w innej bazie.











































n

1

T

n

1

A













A - macierz przejścia z bazy

 do bazy 

Własności macierzy przejścia z bazy do bazy:
1. macierz przejścia z dowolnej bazy

 do dowolnej bazy  tej samej przestani liniowej V jest nieosobliwa (odwracalna).

2. jeśli A jest macierzą przejścia z bazy

 do bazy  A: (

1

,



2

,…,



n

)

B(

1

,



2

,…,



n

) a macierz B jest macierzą przejścia z

bazy

 do bazy

 B:

(



1

,



2

,…,



n

)

 (



1

,



2

,…,



n

) to macierz B



A jest macierzą przejścia z bazy

 do bazy



(A



B): (



1

,



2

,…,



n

)

 (



1

,



2

,…,



n

)

3. Jeżeli A jest macierzą przejścia z bazy

 do bazy  A: (

1

,



2

,…,



n

)

(

1

,



2

,…,



n

) to macierz odwrotna A

-1

jest macierzą

przejścia od bazy

 do bazy  A

-1

: (



1

,



2

,…,



n

)

(

1

,



2

,…,



n

)

34. Określić odwzorowanie (

przekształcenie) liniowe.

Niech U i V będą przestrzeniami liniowymi nad ciałem K. Przekształcenie A:U

V nazywamy liniowym, gdy jest ono

homomorfizmem przestrzeni U w przestrzeń V, czyli:
1.

x,yU A(x+y)=A(x)+A(y) - (addytywność),

2.

cK xU A(cx)=cA(x) - (jednorodność).

Jądrem przekształcenia liniowego A:U

V nazywamy zbiór Ker(A)={xU : Ax=}. Jądro nie może być zbiorem pustym.

Należy do niego na pewno wektor zerowy.

35. Związek odwzorowania liniowego z macierzą.

Dla każdego przekształcenia istnieje macierz zwana macierzą przekształcenia taka że f(x)=A

v (A- macierz, v-wektor) związek

ten pokazuje że macierz jest funkcją.

36. Wektor własny przekształcenia liniowego.

Niech A będzie przestrzenią liniową nad ciałem K i niech x

A. Jeżeli równanie Ax=x , gdzie C, jest spełnione to wektor x

nazywamy wektorem własnym macierzy (przekształcenia), a liczbę

 – wartością własną macierzy.

A

x-x=

A

x-Ex=

A-E)x=

Jest to macierz układu n równań z n niewiadomymi. Macierzą współczynników tego układu jest macierz A-

E, a układ jest

jednorodny zatem ma rozwiązanie. Jeżeli jest to układ Cramera to ma dokładnie jedno rozwiązanie i jest to rozwiązanie
zerowe, ale wektor zerowy nie może być wektorem własnym. Wynika z tego, że powyższy układ nie jest układem Cramera.























nn

n

n

a

a

a

a

A











1

1

11





































nn

n

n

a

a

a

a

E

A











1

1

11

37. Równanie charakterystyczne macierzy i jego pierwiastki – wartości własne macierzy.

Wyznacznik macierzy A-

E w postaci rozwiniętej jest wielomianem zmiennej  stopnia n:











nn

n

n

a

a

a

a











1

1

11

(-1)

n



n

+C

n-1



n-1

+ C

n-2



n-2

+…+ C

1

+C

0

Równanie charakterystyczne macierzy: (-1)

n



n

+C

n-1



n-1

+ C

n-2



n-2

+…+ C

1

+C

0

=0

Pierwiastki tego równania nazywamy wartościami własnymi macierzy.

38. Podać twierdzenie Ceyleya – Hamiltona (dowód).

Jeżeli A jest macierzą kwadratową, a wielomian C(

) jest wielomianem charakterystycznym to C(A)=0

(macierz zerowa)

.

Dowód:
Niech będzie dana macierz A=[a

ij

]

n

m

i wieloman charakterystyczny macierzy A C(

)=C

n



n

+ C

n-1



n-1

+…+ C

1

+C

0

(C

n

=(-1)

n

)

det(A-

E)=C()

Weźmy macierz A-

E i jej dopełnienie algebraiczne. Dopełnienie algebraiczne A

ij

macierzy A-

E jest wielomianem zmiennej 

stopnia co najwyrzej n-1.
A

ij

=(A-

E)

ij

[(A-

E)]

T

=D

n-1



n-1

+D

n-2



n-2

+…+D

1

+D

0

, gdzie D

i

są macierzami stopnia



(A-

E)[(A-E)]

T

=det(A-

E)E=C(E

C(

E=(A-E)(D

n-1



n-1

+D

n-2



n-2

+…+D

1

+D

0

)

Z drugiej strony C(

E=(C

n

E)

n

+(C

n-1

E)

n-1

+…+(C

1

E)+C

0

E

-D

n-1



n

= C

n

E

n

-D

n-1

= C

n

E /A

n

A

D

n-1

- D

n-2

= C

n-1

E /A

n-1

A

D

n-2

- D

n-3

= C

n-2

E /A

n-2

… A

D

1

- D

0

= C

1

E /A

A

D

0

= C

0

E

- A

n

D

n-1

= C

n

E A

n

A

n

D

n-1

- A

n-1

D

n-2

= C

n-1

A

n-1

A

n-1

D

n-2

- A

n-2

D

n-3

= C

n-1

A

n-2

… A

2

D

1

- A

D

0

= C

1

A

A

D

0

= C

0

E

0= C

n

A

n

+ C

n-1

A

n-1

+…+ C

1

A +C

0

E

C(A)=0

Zastosowanie twierdzenia Caley’a-Hamiltona: dzięki temu twierdzeniu możemy w łatwy sposób wyznaczyć wartości

wielomianu.

39. Określić iloczyn skalarny w przestrzeni liniowej.

Iloczyn skalarny wektorów wyraża się wzorem



cos







v

u

v

u











Wynik iloczynu skalarnego jest liczbą.
Iloczyn skalarny wyrażony przez współrzędne wektorów a i b wygląda następująco:

y

y

x

x

y

x

y

x

v

u

v

u

v

v

u

u

v

u











]

,

[

]

,

[









Jeżeli dwa wektory są prostopadłe (ortogonalne) to iloczyn skalarny jest równy 0.

40. Macierze podobne. Diagonalizacja macierzy.

Dwie macierze kwadratowe A i B (n

n) nazywamy macierzami podobnymi jeżeli istnieje macierz nieosobliwa P (nn) taka,

że B=P

-1

AP. Macierze podobne A i B są macierzami tego samego odwzorowania liniowego A:R

n

R

n

, B:R

n

R

n

ale macierz A

jest macierzą przekształcenia w bazie standardowej a macierz B jest macierzą tego samego przekształcenia ale w innej bazie,

zaś macierz P jest macierzą przejścia z bazy do bazy.

Jeżeli macierz A(n

n) jest podobna do macierzy diagonalnej D to mówimy że macierz A jest diagonalizowalną. Proces

znajdowania macierzy D i P nazywamy diagonalizacją macierzy.

Macierz kwadratowa A(n

n) jest podobna do macierzy diagonalnej w tedy i tylko w tedy gdy istnieje baza B={w

1

,w

2

,…,w

n

}

złożona z wektorów własnych macierzy A.

41. Określić działania na wektorach w przestrzeni trójwymiarowej.

Wektorem nazywamy uporządkowaną parę punktów.
Cechy wektora:

- kierunek (kierunek prostej na której leży wektor) 2 wektory mają ten sam kierunek, jeżeli leżą na dwóch równoległych

prostych.

- zwrot (jeden z dwóch sposobów uporządkowania punktów na prostej)
- odległość (odległość początku od końca wektora) szczególnym przypadkiem jest wektor zerowy. Jego długość jest równa 0 i

może przyjąć dowolny kierunek i zwrot.

Działania na wektorach:
- dodawanie wektorów (v

x

, v

y

, v

z

) + (u

x

, u

y

, u

z

) =(v

x

+u

x

, v

y

+u

y

, v

z

+ u

z

) , reguła równoległoboku.

- mnożenie wektora przez liczbę

v

a

v









'

- iloczyn skalarny



cos







v

u

v

u











,

z

z

y

y

x

x

v

u

v

u

v

u

v

u



















Własności:
-

0



v

u









v

u



 

- ortogonalność

- iloczyn skalarny jest dodatni gdy kąt między wektorami jest z przedziału (0,

2



) ujemny gdy (

2



,





- iloczyn wektorowy – iloczynem wektorowym 2 wektorów nazywamy wektor, który jest prostopadły do płaszczyzny

utworzonej przez te wektory, a jego zwrot jest zgodny z regułą śruby prawostronnej. Długość wektora wyraża się wzorwm:



sin









v

u

v

u









,

z

y

x

z

y

x

v

v

v

u

u

u

k

j

i

v

u















Własności:
-

0



 v

u









v

u





||

- kolinearność

- wartość liczbowa iloczynu wektorowego jest równa wartości liczbowej pola powierzchni równoległoboku rozpiętego przez

wektory, które są czynnikami tego iloczynu wektorowego.

- iloczyn mieszany

z

y

x

z

y

x

z

y

x

w

w

w

v

v

v

u

u

u

w

v

u













)

(

Własności:
-

0

)

(





w

v

u













wektory

u



,

v



,

w



leżą w jednej płaszczyźnie – komplanarność

- wartość bezwzględna iloczynu mieszanego jest równa objętości równoległościanu rozpiętego przez te wektory

42. Określić wektor w postaci analitycznej (w układzie kartezjańskim).

k

v

j

v

i

v

v

z

y

x















, gdzie wektory

i



,

j



,

k



są wektorami jednostkowymi osi x, y, z.

43. Podać sposoby wyliczania iloczynu wektorowego wektorów.

z

y

x

z

y

x

v

v

v

u

u

u

k

j

i

v

u















44. Warunki równoległości i prostopadłości wektorów.

Wektory są prostopadłe gdy ich iloczyn skalarny jest równy 0 :

0



v

u









v

u



 

- ortogonalność

Wektory są równoległe gdy ich iloczyn wektorowy jest równy 0 :

0



 v

u









v

u





||

- kolinearność

45. Podać znane postaci równania płaszczyzny. Wyprowadzić równanie parametryczne płaszczyzny.

- równanie normalne płaszczyzny przechodzącej przez punkt P

0

=(x

0

,y

0

,z

0

) i prostopadłej do wektora

n



=[A,B,C] ma postać :

: A(x-x

0

)+B(y-y

0

)+ C(z-z

0

)=0

- równanie ogólne płaszczyzny

: Ax+By+Cz+D=0 A

2

+B

2

+C

2

>0

- równanie parametryczne płaszczyzny przechodzącej przez punkt P

0

=(x

0

,y

0

,z

0

) i rozpiętej na wektorach

u



=[u

x

,u

y

,u

z

]

v



=[v

x

,v

y

,v

z

] ma postać:

x=x

0

+tu

x

+kv

x

:

y=y

0

+tu

y

+kv

y

gdzie k,t

R

z=z

0

+tu

z

+kv

z

- równanie odcinkowe płaszczyzny odcinającej na osiach 0x, 0y, 0z układu współrzędnych odpowiednie odcinki a, b ,c ma

postać:

:

1







c

z

b

y

a

x

Wyprowadzenie równania parametrycznego płaszczyzny:

Niech dana będzie płaszczyzna



rozpięta na dwóch wektorach

u



=[u

x

,u

y

,u

z

]

v



=[v

x

,v

y

,v

z

] i przechodząca przez punkt

P

0

=(x

0

,y

0

,z

0

). Oznaczmy dowolny punkt P(x,y,z) tej płaszczyzny. Wektor



P

P

0

=t



u



+k



v



. Wektory wodzące tych punktów

wynoszą



0

OP

=

0

r



=[x

0

,y

0

,z

0

] oraz



OP

=

r



=[x,y,z]. Zgodnie z regułą równoległoboku otrzymujemy

r



=

0

r



+



P

P

0

co po

podstawianiu daje równanie wektorowe płaszczyzny:

r



=

0

r



+t



u



+k



v



. Podstawiając współrzędne wektorów otrzymujemy

równanie (x,y,z)=( x

0

,y

0

,z

0

)+ t

(u

x

,u

y

,u

z

)+k

(v

x

,v

y

,v

z

). Następie to równanie można przedstawić w formie rozwiniętej:

:









































z

z

y

y

x

x

v

k

u

t

z

z

v

k

u

t

y

y

v

k

u

t

x

x

0

0

0

.

46. Wyprowadzić wzór na obliczanie odległości punktu od płaszczyzny.

Odległość punktu P=(x

1

, y

1

, z

1

) od płaszczyzny

: Ax+By+Cz+D=0 przedstawia wzór: d(P,)=

2

2

2

1

1

1

C

B

A

Cz

By

Ax









47. Równania prostej w przestrzeni trójwymiarowej.

- równanie parametryczne prostej przechodzącej przez punkt P

0

=(x

0

,y

0

,z

0

) i wyznaczonej przez niezerowy wektor kierunku

v



=[v

x

,v

y

,v

z

] ma postać:

x=x

0

+tv

x

l:

y=y

0

+tv

y

gdzie t

R

z=z

0

+tv

z

- równanie kierunkowe prostej: l:

z

y

x

v

z

z

v

y

y

v

x

x

0

0

0











- równanie krawędziowe prostej która jest częścią wspólną dwóch nierównoległych płaszczyzn





: A

1

x+B

1

y+C

1

z+D

1

=0 i





: A

2

x+B

2

y+C

2

z+D

2

=0 ma postać:























0

0

2

2

2

2

1

1

1

1

D

z

C

y

B

x

A

D

z

C

y

B

x

A

48. Wyprowadzić równanie prostej w postaci parametrycznej i kierunkowej.

Niech będzie dana prosta l przechodząca przez punkt P

0

=(x

0

,y

0

,z

0

) i o wektorze kierunkowym

v



=[v

x

,v

y

,v

z

]. Wektor wodzący

punkt P

0

ma postać



0

OP

=

0

r



=[x

0

,y

0

,z

0

]. Obierzmy dowolny punkt P(x,y,z) należący do tej prostej i o wektorze wodzącym



OP

=

r



=[x,y,z]. Wektor



P

P

0

=t



v



. Zgodnie z regułą równoległoboku otrzymujemy



OP

=



0

OP

+



P

P

0

co po podstawianiu

daje równanie wektorowe prostej

r



=

0

r



+t



v



. Rozpisując to równanie na współrzędne otrzymujemy (x,y,z)=( x

0

,y

0

,z

0

)+

t

(v

x

,v

y

,v

z

). Następie to równanie można przedstawić w formie rozwiniętej:

:





























z

y

x

v

t

z

z

v

t

y

y

v

t

x

x

0

0

0

. Równanie kierunkowe prostej

otrzymujemy po wyrugowaniu parametru t:





























z

z

y

y

x

x

v

v

t

z

z

v

v

t

y

y

v

v

t

x

x

:

/

:

/

:

/

0

0

0

=

































t

v

z

z

t

v

y

y

t

v

x

x

z

y

x

0

0

0

z

y

x

v

z

z

v

y

y

v

x

x

t

0

0

0













.

49. Omówić wzajemne położenie prostych, płaszczyzn oraz prostej i płaszczyzny w przestrzeni

trójwymiarowej

1. położenie dwóch płaszczyzn

- odległość między płaszczyznami równoległymi





: Ax+By+

1

z+D

1

=0 i





: Ax+By+Cz+D

2

=0 wyraża się równaniem:

2

2

2

2

1

2

1

)

,

(

C

B

A

D

D

d













- kąt między dwoma płaszczyznami





: A

1

x+B

1

y+C

1

z+D

1

=0 i





: A

2

x+B

2

y+C

2

z+D

2

=0

o wektorach normalnych

1

n



=[A

1

,B

1

C

1

],

2

n



=[A

2

,B

2

,C

2

] :

2

2

2

2

2

2

2

1

2

1

2

1

2

1

2

1

2

1

cos

C

B

A

C

B

A

C

C

B

B

A

A

























lub

2

1

2

1

arccos

n

n

n

n

















2. położenie prostej i płaszczyzny

- kąt nachylenia prostej l o wektorze kierunkowym

v



do płaszczyzny

 o wektorze normalnym

n



wyraża się wzorem:

v

n

v

n

l



















arcsin

)

,

(

3. położenie dwóch prostych

- kąt miedzy prostymi l

1

,l

2

o wektorach kierunkowych

1

v



i

2

v



wyraża się wzorem:

2

1

2

1

2

1

arccos

)

,

(

v

v

v

v

l

l

















50. Definicja okręgu i jego równanie.

Niech S = (x

0

,y

0

) będzie ustalonym punktem, zaś r odcinkiem o dodatniej długości. Okręgiem nazywamy zbiór punktów

płaszczyzny euklidesowej odległych od punktu S o zadaną odległość r.
Równania okręgu:

(

x

−

x

0

)

2

+ (

y

−

y

0

)

2

=

r

2

- jest to wzór geometrii analitycznej obowiązujący w kartezjańskim układzie

współrzędnych. W tym samym układzie współrzędnych okrąg może być opisany również za pomocą równania

parametrycznego:



















sin

cos

0

0

r

y

y

r

x

x

gdzie parametr (0,2). Podstawiając do wzoru geometrii analitycznej

r=

c

y

x





2

0

2

0

otrzymujemy równanie: x

2

+y

2

-2x

0

x-2y

0

y+c=0

51. Definicja hiperboli i jej równanie

.

Hiperbola jest krzywą stożkową, będąca zbiorem punktów takich, że bezwzględna wartość różnicy odległości tych punktów

od dwóch punktów, nazywanych ogniskami hiperboli, jest stała. Jeżeli ogniska hiperboli mają współrzędne (-c,0) i (c,0) to

hiperbola jest opisana równaniem:

1

2

2

2

2





b

y

a

x

gdzie a, to połowa odległości pomiędzy wierzchołkami hiperboli, zaś b to

połowa odległości pomiędzy wierzchołkami urojonymi. Zachodzi również związek:

b

2

=

c

2

−

a

2

. Hiperbole można jeszcze

opisać równaniem:

0

0

2

2

2

2

2

2

2

2

2

2

2

2













a

b

y

a

x

b

a

b

y

a

x

b

.

Jeżeli a = b to hiperbolę nazywamy równoosiową.

52. Definicja paraboli i jej równanie.

Parabola to krzywa stożkowa utworzona przez przecięcie stożka płaszczyzną równoległą do tworzącej stożka. Parabolę

można też zdefiniować jako miejsce geometryczne punktów równo odległych od prostej (zwanej kierownicą paraboli) i
pewnego punktu (ogniska paraboli) nie leżącego na tej prostej. W kartezjańskim układzie współrzędnych, parabola z osią

symetrii równoległą do osi

y

, wierzchołkiem o współrzędnych (

h

,

k

), ogniskiem (

h

,

k

+

p

), i kierownicą

y

=

k

-

p

opisana jest

równaniem: (x-h)

2

=2p(y-k). Parabolę można również opisać wzorem:

0

2

0

2

2

2









py

x

y

px

. Parabola ma jedną oś symetrii, która

przechodzi przez ognisko i wierzchołek i jest prostopadła do kierownicy paraboli.

53. Kwadrygi – ich klasyfikacja.

Niech będzie dany układ kartezjański OXYZ. Powierzchnią stopnia drugiego nazywamy miejsce geometryczne punktów,

których współrzędne spełniają równanie : a

11

x

2

+a

22

y

2

+2a

33

z

2

+2a

12

xy+2a

13

xz+2a

23

xz+2a

10

x+2a

20

y+2a

30

z+a

00

=0 przy

założeniu, że a

11

2

+a

22

2

+a

33

2

+a

12

2

+a

13

2

+a

23

2

>0.

1. Sfera:

2

2

2

2

r

z

y

x







;

2

2

2

2

)

(

)

(

)

(

r

c

z

b

y

a

x













,

gdzie a, b, c to współrzędne środka sfery.

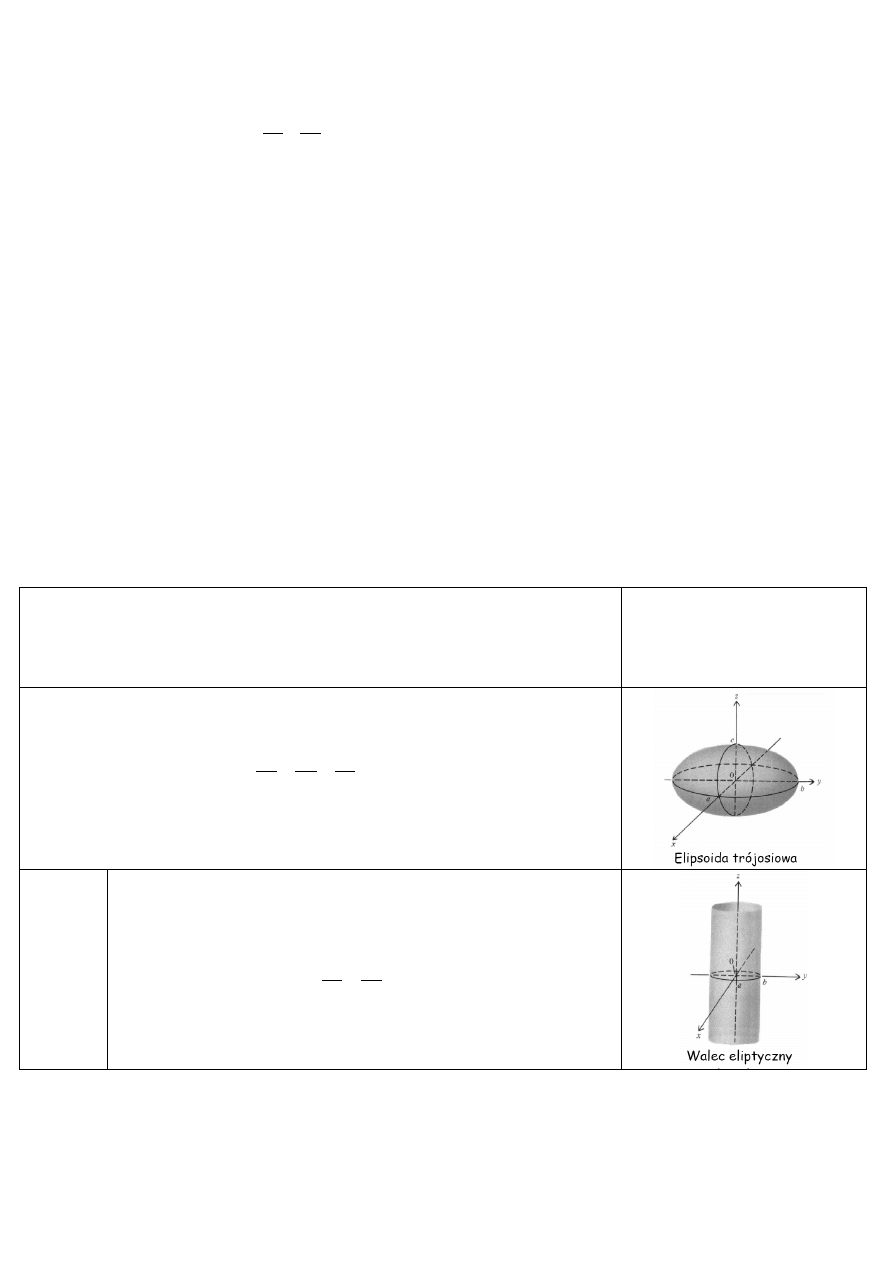
2. Elipsoida:

1

2

2

2

2

2

2







c

z

b

y

a

x

,

gdzie a, b, c to „promienie” odpowiednio na osiach OX, OY, OZ

3. Walce:

Eliptyczny (równoległy do z):

1

2

2

2

2





b

y

a

x

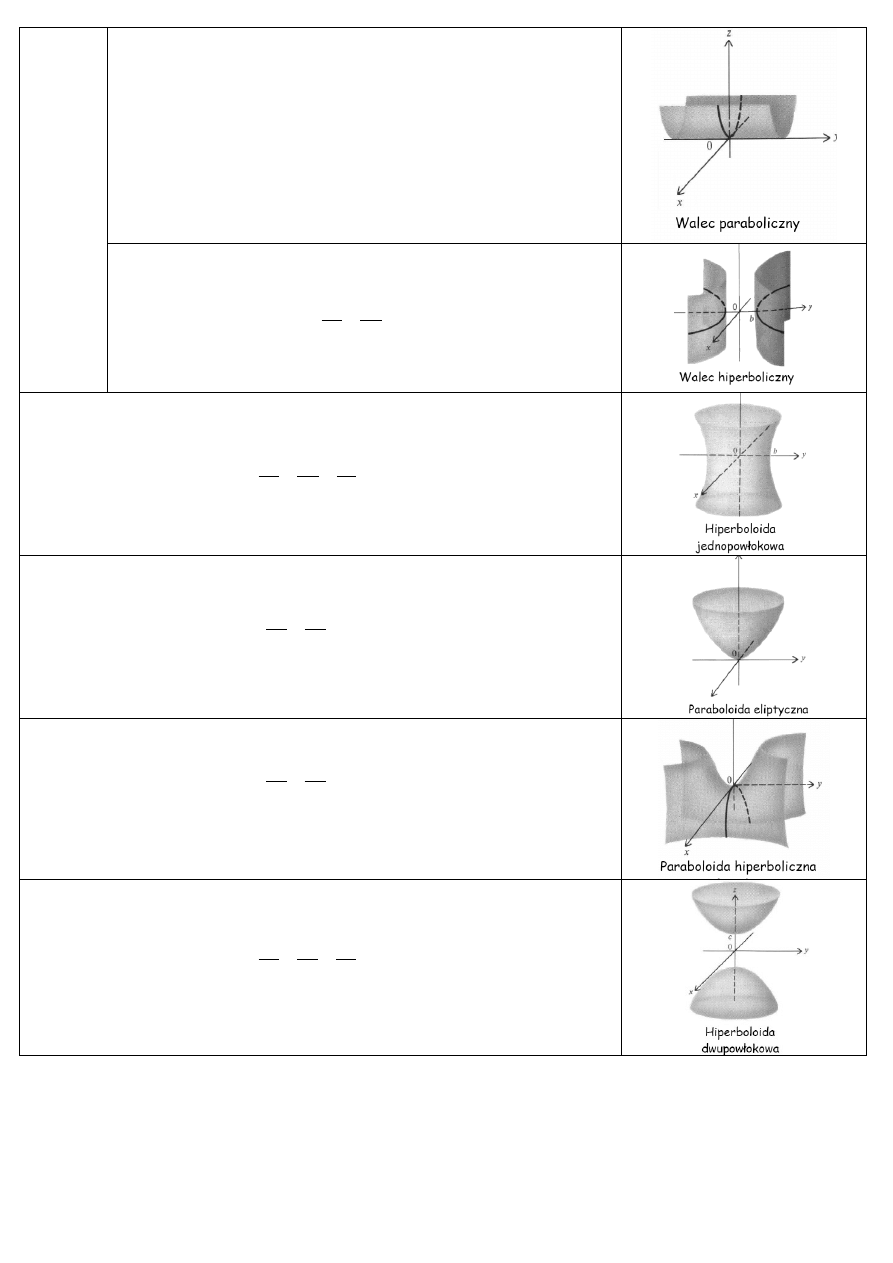
Paraboliczny:

px

y

2

2



,

gdzie p to parametr

22

11

a

a

p





Hiperboliczny:

1

2

2

2

2





b

y

a

x

4. Hiperbola jedno powłokowa:

1

2

2

2

2

2

2







c

z

b

y

a

x

5. Paraboloida eliptyczna:

pz

b

y

a

x

2

2

2

2

2





gdy p>0 to jest skierowany do góry a jak p<0 to w dół.

6. Paraboloida hiperboliczna:

pz

b

y

a

x

2

2

2

2

2





gdy p<0 to wygląda jak siodło, a jak p>0 to nie wiem.

7. Hiperboloida dwu powłokowa:

1

2

2

2

2

2

2







c

z

b

y

a

x

54. Podać równanie sfery i elipsoidy. Które z tych powierzchni są obrotowe?

Sfera:

2

2

2

2

r

z

y

x







;

2

2

2

2

)

(

)

(

)

(

r

c

z

b

y

a

x













, gdzie a, b, c to współrzędne środka sfery

Elipsoida:

1

2

2

2

2

2

2







c

z

b

y

a

x

, gdzie a, b, c to „promienie” odpowiednio na osiach OX, OY, OZ

Co o do powierzchni obrotowych to nie jestem pewien, ale z zadań które były liczone to wynika ze elipsoida jest (dwie
spośród a, b, c musi być liczbą niewymierną, np. a i c).

55. Wymień znane paraboloidy i podaj ich równania

.

Paraboloida to nieograniczona powierzchnia drugiego stopnia posiadająca jedną oś symetrii.
Wyróżnia się 3 typy paraboloid:

- paraboloida obrotowa x

2

+ y

2

= a

2

z

- paraboloida eliptyczna

pz

b

y

a

x

2

2

2

2

2





-

paraboloida hiperboliczna

pz

b

y

a

x

2

2

2

2

2





56. Wymień znane hiperboloidy i podaj ich równania.

Hiperboloida - nieograniczona, nierozwijalna powierzchnia drugiego stopnia (kwadryka), powstała przez obrót hiperboli

wokół osi rzędnych (hiperboloida jednopowłokowa) lub osi odciętych (hiperboloida dwupowłokowa), a także każda otrzymana
z takiej przez przekształcenie afiniczne przestrzeni. Każda hiperboloida ma środek symetrii oraz co najmniej trzy osie i trzy

płaszczyzny symetrii.

- hiperboloida jednopowłokowa

1

2

2

2

2

2

2







c

z

b

y

a

x

- hiperboloida dwupowłokowa

1

2

2

2

2

2

2







c

z

b

y

a

x

- hiperboloida której obie powłoki mają dokładnie jeden punkt wspólny

0

2

2

2

2

2

2







c

z

b

y

a

x

57. Określić powierzchnię walcową i napisać równania znanych walców.

Powierzchnię walcową nazywamy powierzchnię utworzona przez zbiór prostych (tworzących powierzchnię walcową)

równoległych do danej prostej i przechodzących przez punkty krzywej L (kierownicy).

- walec eliptyczny:

1

2

2

2

2





b

y

a

x

- walec paraboliczny:

px

y

2

2



, gdzie p to parametr

22

11

a

a

p





- walec hiperboliczny:

1

2

2

2

2





b

y

a

x

58. Określić powierzchnię stożkową i napisać równania znanych stożków.

Powierzchnia stożkowa - powierzchnia powstała przez połączenie prostymi (tzw. tworzące) zadanego punktu w przestrzeni
(tzw. wierzchołek) z każdym punktem na pewnej zadanej krzywej, zwanej kierującą.