1

Matematyka finansowa

Ćwiczenie 8

(rachunek kredytów)

4. (7.40) Zaciągnięto kredyt w wysokości 10 000 zł oprocentowany 24% w stosunku rocznym. Uzgodniono
następujące warunki spłaty:

a) cztery równe raty płatne po drugim, piątym, dziewiątym i dwunastym miesiącu;
b) cztery równe raty płatne po drugim, szóstym, dziesiątym i dwunastym miesiącu;
c) cztery równe raty płatne po czwartym, ósmym, dziesiątym i dwunastym miesiącu;
d) cztery raty płatne po czterech kolejnych kwartałach w wysokości 20% należnej kwoty, 25% należnej kwoty,

25% należnej kwoty, resztę należnej kwoty.

Obliczyć wysokość rat.
Odp.: a) 2856,37 zł, b) 2882,78 zł, c) 2940,93 zł, d) 2329,07 zł, 2911,34 zł, 2911,34 zł, 3493,61 zł.

Rozwiązanie

a) Oprocentowanie w skali miesiąca jest równe 2%. Niech x będzie wysokością raty umorzeniowej. Wyznaczamy
wysokość rat rozwiązując równanie:

000

10

06

,

1

08

,

1

06

,

1

04

,

1

08

,

1

06

,

1

04

,

1

06

,

1

04

,

1

04

,

1

=

⋅

⋅

⋅

+

⋅

⋅

+

⋅

+

x

x

x

x

,

37

,

2856

=

x

.

d) Niech

(

)

4

,...,

1

1

=

i

R

oznacza wysokość i - tej raty umorzeniowej. Ustalamy proporcje między wysokością rat.

Z treści zadania wynika, że druga i trzecia rata są o 25% wyższe od pierwszej, a ostatnia jest o 50% wyższa od
pierwszej:

1

4

1

3

1

2

5

,

1

,

25

,

1

,

25

,

1

R

R

R

R

R

R

⋅

=

⋅

=

⋅

=

. Równanie umorzeniowe przyjmuje postać:

000

25

15

,

1

5

,

1

15

,

1

25

,

1

15

,

1

25

,

1

15

,

1

4

1

3

1

2

1

1

=

⋅

+

⋅

+

⋅

+

R

R

R

R

.

Rozwiązaniem równania jest

.

07

,

2329

1

=

R

Znajomość

1

R

pozwala na wyznaczenie wartości pozostałych rat:

34

,

2911

07

,

2329

25

,

1

25

,

1

1

2

=

⋅

=

⋅

=

R

R

zł,

34

,

2911

07

,

2329

25

,

1

25

,

1

1

3

=

⋅

=

⋅

=

R

R

zł,

61

,

3493

07

,

2329

5

,

1

5

,

1

1

4

=

⋅

=

⋅

=

R

R

zł.

5. (7.33) Zaciągnięto kredyt w wysokości 25 000 zł na 15% rocznie. Kredyt ma być spłacony w czterech rocznych
ratach. Rata druga ma być o 20% wyższa od pierwszej, rata trzecia 10% niższa od drugiej, zaś suma rat pierwszej i
trzeciej ma być 20% większa od sumy rat drugiej i czwartej. Znajdź wysokość rat.
Odp.: 8954,19 zł, 10 745,03 zł, 9670,53 zł, 4775,57 zł.

Rozwiązanie

Niech

(

)

4

,...,

1

1

=

i

R

oznacza wysokość i - tej raty umorzeniowej. Równanie umorzeniowe przyjmuje postać:

000

25

15

,

1

15

,

1

15

,

1

15

,

1

4

1

3

3

2

2

1

=

+

+

+

R

R

R

R

.

Oznaczmy przez

R

nieznaną ratę umorzeniową będącą punktem odniesienia przy wyznaczania wysokości

1

R

czterech rat umorzeniowych. Niech

4

,...,

1

,

1

=

⋅

=

i

R

R

i

α

. Wartości

i

α wyznaczają relacje między wysokością rat.

J.Marcinkowski Rachunek kredytów

2

Korzystając z zależności

4

,...,

1

,

1

=

⋅

=

i

R

R

i

α

, równanie umorzeniowe zapisujemy w następującej postaci:

000

25

15

,

1

15

,

1

15

,

1

15

,

1

4

4

3

3

2

2

1

=

⋅

+

⋅

+

⋅

+

⋅

R

R

R

R

α

α

α

α

.

Ustalamy zależności zachodzące między

i

α :

1

2

2

,

1

α

α

=

(rata druga ma być o 20% wyższa od pierwszej),

2

3

9

,

0

α

α

=

(rata trzecia ma być 10% niższa od drugiej),

(

)

4

2

3

1

2

,

1

α

α

α

α

+

=

+

(suma rat pierwszej i trzeciej ma być o 20% większa od sumy rat drugiej i czwartej).

Otrzymaliśmy układ trzech równań z czterema niewiadomymi. W celu wyznaczenia jego rozwiązania przyjmujemy,
że

1

1

=

α

i dołączamy to równanie do układu równań. Arbitralne określenie wartości

1

α nie powoduje żadnych

komplikacji, gdyż zależy nam na ustaleniu proporcji między wysokością rat, a nie ich wysokości: znając proporcje
bez trudu wyznaczymy ich wysokość.

Rozwiązaniem układu równań jest

533

,

0

,

08

,

1

,

2

,

1

,

1

4

3

2

1

=

=

=

=

α

α

α

α

. Podstawiając otrzymane wartości do

równania umorzeniowego otrzymujemy:

000

25

15

,

1

533

,

0

15

,

1

08

,

1

15

,

1

2

,

1

15

,

1

1

4

3

2

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

+

⋅

R

,

19

,

8954

=

R

.

Znajomość

i

α oraz

R

pozwala na wyznaczenie wysokości rat umorzeniowych:

19

,

8954

19

,

8954

1

1

=

⋅

=

⋅

=

R

R

i

α

zł,

03

,

745

10

19

,

8954

2

,

1

2

2

=

⋅

=

⋅

=

R

R

α

zł,

53

,

9670

19

,

8954

08

,

1

3

3

=

⋅

=

⋅

=

R

R

α

zł,

6. (7.38) Zaciągnięto kredyt w wysokości 12 000 zł oprocentowany na 24%. Uzgodniono następujące warunki
spłaty: cztery raty w równej wysokości płatne po drugim, szóstym, ósmym i dwunastym miesiącu. Dłużnik
nieoczekiwanie otrzymał spadek i chce spłacić kredyt już po szóstym miesiącu. Jaka powinna być wysokość
ostatniej raty? Oblicz wartość nominalną kwoty zaoszczędzonej dzięki wcześniejszej spłacie.
Odp.: Rata: 9776,16 zł; zaoszczędzono 507,84 zł.

Rozwiązanie

Oprocentowanie w skali miesiąca jest równe 2%. Niech x będzie wysokością raty umorzeniowej. Wyznaczamy
wysokość raty w przypadku spłaty rat zgodnie z ustalonym harmonogramem:

000

12

04

,

1

04

,

1

08

,

1

04

,

1

04

,

1

08

,

1

04

,

1

08

,

1

04

,

1

04

,

1

=

⋅

⋅

⋅

+

⋅

⋅

+

⋅

+

x

x

x

x

,

99

,

3427

=

x

Bieżąca wartość pozostałej po spłacie pierwszej raty części kredytu jest równa:

86

,

8703

04

,

1

99

,

3427

000

12

=

−

.

Wartość przyszła (na moment spłaty po 6 miesiącu) pozostałego do spłaty kredytu jest równa

86

,

9776

08

,

1

04

,

1

86

,

8703

=

⋅

⋅

.

Nominalna wartość zaoszczędzonej kwoty wyraża się wzorem:

84

,

507

86

,

9776

99

,

3427

3

=

−

⋅

.

J.Marcinkowski Rachunek kredytów

3

Wyznaczając wartość nominalną zaoszczędzonej kwoty od wartości trzech pozostałych po upływie 6 miesięcy do
spłaty rat odejmujemy wysokość ostatniej raty. Przedstawiony sposób wyznaczania zaoszczędzonej kwoty może
budzić wątpliwości, gdyż przy jego obliczaniu sumowaliśmy wysokości rat płatne w różnych momentach czasu
(więc nieporównywalne).

7. (7.32) Pożyczono 10 000 zł na pół roku. Dług należy zwrócić w dwóch równych ratach płatnych po trzecim i po
szóstym miesiącu. Wysokość każdej raty wynosi 6000 zł. Oblicz roczną stopę oprocentowania pożyczki.
Odp.: 52,26%.

Rozwiązanie

Wyznaczamy wartość czynnika dyskontującego v , dla której spełniona jest równość:

000

1

6000

6000

2

=

⋅

+

⋅

v

v

.

Rozwiązujemy równanie kwadratowe

1

:

0

10

6

6

2

=

−

+ v

v

.

Jego pierwiastkami są:

8844

,

0

12

276

6

;

0

12

276

6

2

1

=

+

−

=

<

−

−

=

x

x

.

Ze względu na wymaganą nieujemność v odrzucamy pierwszy pierwiastek i wyznaczamy oprocentowanie
odpowiadające v równemu

8844

,

0

. Rozwiązujemy równanie:

8844

,

0

1

1 =

+ p

.

Poszukiwaną wartością

p

jest

130764

,

0

, z czego wynika, że stopa oprocentowania kredytu jest równa

%)

26

,

52

(

5225

,

0

130764

,

0

4

≈

⋅

.

8. (7.29) W sprzedaży ratalnej wpłacono 20 zł jako 7% opłatę manipulacyjną. Jaka będzie wysokość równych rat
spłacanych na koniec 12 kolejnych miesięcy, jeżeli stopa procentowa wynosi 15%?
Odp.: 25,79 zł.

Rozwiązanie

Oznaczmy przez

K

wysokość kredytu. Wyznaczamy jego wysokość korzystając z informacji, że 7% kredytu to 20

zł:

1

07

,

0

20

K

=

,

71

,

285

=

x

.

Miesięczne oprocentowanie kredytu wynosi

%)

25

,

1

(

0125

,

0

12

15

,

0

=

. Wysokość rat wyznaczamy z równania:

(

)

71

,

285

0125

,

1

...

0125

,

1

12

=

+

+

x

x

.

Korzystając ze wzoru na sumę skończonego ciągu geometrycznego otrzymujemy:

1

Podzielenie współczynników równania kwadratowego przez stałą dodatnią nie zmienia wartości pierwiastków równania.

J.Marcinkowski Rachunek kredytów

4

71

,

285

0125

,

1

1

1

0125

,

1

1

1

0125

,

1

1

12

=

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

⋅

x

,

79

,

25

=

x

.

9. (7.10) Kredytobiorca zaciąga roczny kredyt oprocentowany na 10%, przy czym odsetki są potrącane z góry, to jest
w całości pobierane z pożyczonej kwoty przy jej wypłacie. Ponadto w momencie wypłaty kredytobiorca płaci
bankowi 3% prowizji. Cały pożyczony kapitał jest spłacany w jednej racie po roku. Obliczyć RRSO tego kredytu.
Odp.: RRSO: 0,1494 = 14,94%.

Rozwiązanie

Wysokość zaciągniętego kredytu: K .
Odsetki:

K

1

,

0

.

Prowizja:

K

03

,

0

.

Do dyspozycji kredytobiorcy (kapitał netto) pozostaje

K

87

,

0

.

Rata kredytu płatna po upływie roku: K .

Rzeczywistą stopę oprocentowania kredytu p~ (RRSO) wyznaczamy z równania:

(

)

K

K

p

=

⋅

+

⋅

~

1

87

,

0

,

%)

94

,

14

(

1494

,

0

~ =

p

.

10. (7.6) Klient zaciągnął w banku kredyt w wysokości 3000 PLN, który spłaci w dwunastu malejących ratach o
stałej części kapitałowej. Bank przy udzieleniu kredytu pobiera prowizję w wysokości 5% kwoty kredytu oraz opłatę
za ubezpieczenie kredytu równą 1,5% kwoty kredytu pomnożoną przez liczbę rat. Nominalna stopa procentowa tego
kredytu wynosi 12%. Obliczyć RRSO zaciągniętego kredytu.
Odp.: RRSO: 0,6584=65,84% .

Rozwiązanie

Wysokość jednej raty kapitałowej: 3000 : 12 = 250.
Nominalna stopa procentowa p wynosi 12%, więc odsetki w każdym miesiącu wynoszą 1% kwoty niespłaconego
kredytu.
Wyznaczamy wysokości poszczególnych rat:

R1 = 250 + 0,01·3000 = 250 + 30 = 280
R2 = 250 + 0,01·2750 = 250 + 27,50 = 277,50
R3 = 250 + 0,01·2500 = 250 + 25 = 275
R4 = 250 + 0,01·2250 = 250 + 22,50 = 272,50
R5 = 250 + 0,01·2000 = 250 + 20 = 270
R6 = 250 + 0,01·1750 = 250 + 17,50 = 267,50
R7 = 250 + 0,01·1500 = 250 + 15 = 265
R8 = 250 + 0,01·1250 = 250 + 12,50 = 262,50
R9 = 250 + 0,01·1000 = 250 + 10 = 260
R10 = 250 + 0,01·750 = 250 + 7,50 = 257,50
R11 = 250 + 0,01·500 = 250 + 5 = 255
R12 = 250 + 0,01·250 = 250 + 2,50 = 252,50

Prowizja: 0,05·3000 = 150 zł.
Ubezpieczenie kredytu: 0,015·3000·12 = 540 zł.
Pożyczony kapitał netto: 3000 – 150 – 540 = 2310 zł.

J.Marcinkowski Rachunek kredytów

5

Rzeczywisty czynnik dyskontujący v~ , gdzie

1

~

1

1

~

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

p

v

,

wyznaczamy rozwiązując równanie

2

:

12

11

10

9

8

7

6

5

4

3

2

~

5

,

252

~

255

~

5

,

257

~

260

~

5

,

262

~

265

~

5

,

267

~

2705

~

5

,

272

~

275

~

5

,

277

~

280

2310

v

v

v

v

v

v

v

v

v

v

v

v

+

+

+

+

+

+

+

+

+

+

+

+

=

94799

,

0

~ =

v

.

Rzeczywista stopa procentowa

p~

zaciągniętego kredytu jest równa:

%)

84

,

65

(

6584

,

0

1

~

1

12

~

=

⎟

⎠

⎞

⎜

⎝

⎛ −

⋅

=

v

p

.

11. (7.37) Kredyt oprocentowany 24% w stosunku rocznym ma być spłacony w dwunastu równych ratach płatnych
na koniec każdego roku. Kredytobiorca nie uregulował czterech pierwszych wpłat i przez następne osiem lat będzie
musiał spłacać raty w wysokości 3600 zł rocznie. W jakiej wysokości został zaciągnięty kredyt?
Odp.: 5209,51 zł.

Rozwiązanie

Wysokość zaciągniętego kredytu

K

wyznaczamy z równania (pierwsza rata jest płatna po 5 miesiącach):

51

,

5209

4471

,

1

3600

24

,

1

1

1

24

,

1

1

1

24

,

1

3600

3600

24

,

1

3600

...

24

,

1

3600

8

5

12

5

=

⋅

=

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

⋅

=

+

+

=

K

.

12. (7.16) Kredyt w wysokości L jest oprocentowany nominalną stopą procentową 5% i może być spłacany przez 20
lat za pomocą jednej z dwóch metod: stałe raty umorzeniowe albo stałe raty kapitałowe. Pierwszą ratę w każdym z
tych przypadków płaci się na końcu pierwszego roku. Wyznaczyć pierwszy rok, w którym spłata ze stałą ratą
kapitałową będzie niższa od stałej raty umorzeniowej.
Odp.: W dziesiątym roku.

Rozwiązanie

Wprowadźmy następujące oznaczenia:

−

R

- rata umorzeniowa;

−

i

RK

- rata ze stałą ratą kapitałową.

Wyznaczamy wysokość raty umorzeniowej:

L

R

R

=

+

+

20

05

,

1

...

05

,

1

,

Kredyt możemy potraktować jako zwykłą rentę czasową. Z punktu widzenia pożyczkodawcy udzielony kredyt jest
funduszem rentowym, a spłaty rat kredytu dokonywane przez dłużnika - wypłatami renty. Korzystając z czynnika
dyskontującego zwykłej renty czasowej otrzymujemy

L

R

=

⋅

−

⋅

05

,

0

05

,

1

1

05

,

1

20

20

,

z czego wynika, że

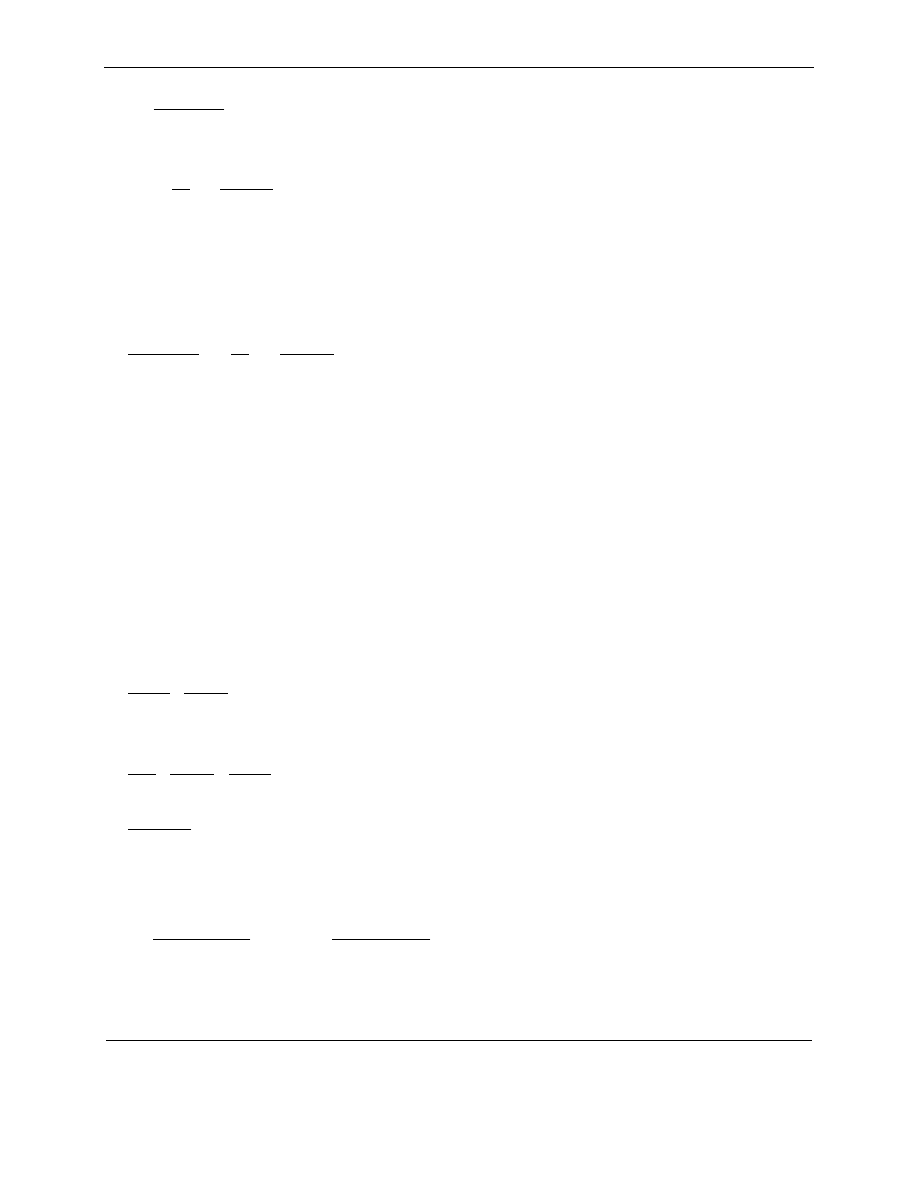
J.Marcinkowski Rachunek kredytów

6

L

L

R

⋅

=

⋅

−

⋅

=

8024

,

0

1

05

,

1

05

,

0

05

,

1

20

20

.

Wyznaczamy wysokość rat ze stałą ratą kapitałową:

20

,...,

1

,

05

,

0

20

1

20

20

1

=

⋅

⋅

+

−

+

⋅

=

i

L

i

L

RK

i

.

Pierwszy składnik sumy określa wysokość części kapitałowej raty, drugi - wysokość odsetek płatnych w danej racie.
Wysokość rat maleje, gdyż odsetki są płatne od zmniejszającego się w postępie arytmetycznym niespłaconego
kapitału.

Szukamy pierwszej raty ze stałą ratą kapitałową niższą od stałej raty umorzeniowej, Wyznaczamy najmniejszą
wartość i , dla której zachodzi nierówność:

L

i

L

L

⋅

⋅

+

−

+

⋅

>

⋅

−

⋅

05

,

0

20

1

20

20

1

1

05

,

1

05

,

0

05

,

1

20

20

.

Po elementarnych przekształceniach otrzymujemy:

903

,

8

>

i

.

Oznacza to, że 9 (płatna w dziesiątym roku) rata ze stałą częścią kapitałową będzie mniejsza od stałej raty
umorzeniowej.

13. (7.30) Udzielono kredytu w wysokości 35 460 zł. Umowa przewiduje, że ma być on spłacony w dwóch równych
ratach po 20 000 zł płatnych kolejno po sześciu i dwunastu miesiącach. Wyznacz stopę procentową kredytu.
Odp.: 16,84%.

Rozwiązanie

Oznaczmy przez r oprocentowanie pro rata (oprocentowanie między kapitalizacjami odsetek):: nominalna stopa
procentowa jest równa r

2

.

Równanie umorzeniowe przyjmuje postać:

(

)

460

35

1

000

20

1

000

20

2

=

+

+

+

r

r

.

Dokonujemy elementarnych przekształceń:

(

)

000

20

460

35

1

1

1

1

2

=

+

+

+

r

r

,

773

,

1

2

1

2

2

=

+

+

+

r

r

r

,

0

227

,

0

546

,

2

773

,

1

2

=

−

+

r

r

.

Pierwiastkami otrzymanego równania kwadratowego są:

0

546

,

3

8466

,

2

546

,

2

1

<

−

−

=

r

,

0842

,

0

546

,

3

8466

,

2

546

,

2

2

=

+

−

=

r

.

Oprocentowanie kredytu wynosi r

2

, tj.

%)

84

,

16

(

1684

,

0

0842

,

0

2

=

⋅

.

2

Metoda rozwiązywania tego rodzaju równań została krótko omówiona przy omawianiu sposobu rozwiązania

zadania 14 (7.18).

J.Marcinkowski Rachunek kredytów

7

14. (7.18) Kredyt w wysokości 10 000 zł będzie spłacany za pomocą 12 rat płatnych na końcu każdego miesiąca.
Wysokość raty wynosi 850 zł. Wyznacz wysokość oprocentowania kredytu.

Rozwiązanie

Oznaczmy przez p oprocentowanie nominalne: wówczas oprocentowanie pro rata (oprocentowanie między
kapitalizacjami odsetek) wynosi

12

p

.

Dla uproszczenia zapisu równanie umorzeniowe zapisujemy korzystając z czynnika dyskontującego v :

(1)

(

)

000

10

...

850

12

=

+

+

⋅

v

v

,

gdzie

(2)

12

1

1

p

v

+

=

.

W ogólnym przypadku

(

]

1

,

0

∈

v

. Z (2) wynika, że jeżeli

,

0

=

p

to

1

=

v

, natomiast dla

∞

→

p

,

0

→

v

.

Zauważmy, że

1

≠

v

. Istotnie,

000

10

200

10

12

850

≠

=

⋅

: suma w nawiasie musi być nieco mniejsza od 1. Tak więc

( )

1

,

0

∈

v

.

Równania (1) nie można rozwiązać metodami analitycznymi (nie istnieją wzory pozwalające wyznaczyć
poszczególne pierwiastki równania). Można je wyznaczyć stosując metody numeryczne.

Poszukując rozwiązań równania (1) skorzystamy z faktu, że równanie to ma jeden pierwiastek dodatni, który zawiera
się w przedziale

( )

1

,

0

.

W celu uproszczenia dalszych obliczeń dokonujemy następujących przekształceń. Zauważamy, że wartość
wyrażenia w nawiasie jest sumą skończonego ciągu geometrycznego, co pozwala zapisać (1) w następującej postaci:

(1)

000

10

1

1

850

12

=

−

−

⋅

⋅

v

v

v

,

prowadząc do równania:

(3)

0

7647

,

11

7647

,

12

13

=

+

−

v

v

.

Pierwiastek równania równy 1 odrzucamy i szukamy pierwiastka (3) zawartego w przedziale

( )

1

,

0

.Wiemy, że

istnieje tylko jeden taki pierwiastek

3

.

Oznaczmy przez

( )

v

f

lewą stronę (3). Będziemy poszukiwać przedziału, w którym znajduje się pierwiastek,

zmniejszając długość tego przedziału w kolejnych iteracjach o połowę. Dokonując wystarczająco dużej liczby
iteracji będziemy mogli wyznaczyć wartość pierwiastka z dowolną, zadaną dokładnością.

Zbadajmy znak

( )

v

f

dla

991

,

0

=

v

oraz

999

,

0

=

v

:

991

,

0

=

v

;

( )

0039642

,

0

=

v

f

,

3

Zauważmy, że równanie

0

1

=

+ v

ma jeden pierwiastek równy -1: 1, v są wyrazami ciągu geometrycznego. Stosując wzór na

sumę ciągu geometrycznego otrzymujemy równanie

0

1

1

2

=

−

−

v

v

, które ma dwa pierwiastki, niemniej zbiór pierwiastków

równania

0

1

=

+

v

jest zawarty w zbiorze pierwiastków równania

0

1

1

2

=

−

−

v

v

. Rozumowanie to można uogólnić na równania

wyższych stopni. Wiedząc, że pierwiastek (1) znajduje się w przedziale

( )

1

,

0

wnioskujemy, że pierwiastek (3) znajdujący się w

tym przedziale ma tę samą wartość.

J.Marcinkowski Rachunek kredytów

8

999

,

0

=

v

;

( )

0001576

,

0

−

=

v

f

.

Ponieważ przy wzroście wartości v od 991

,

0

do 999

,

0

( )

v

f

zmienia znak, w przedziale tym musi istnieć taka

wartość *

v

, dla której

( )

*

v

f

jest równe 0. Wiemy więc, że pierwiastek znajduje się w przedziale

(

)

999

,

0

,

991

,

0

.

Badamy znak

( )

v

f

dla

995

,

0

=

v

(wartości połowiącej przedział):

995

,

0

=

v

;

( )

0007382

,

0

=

v

f

.

Analizując znaki wnioskujemy, że pierwiastek zawiera się w przedziale

(

)

999

,

0

,

995

,

0

. Badamy znak

( )

v

f

dla

997

,

0

=

v

:

997

,

0

=

v

;

( )

0000116

,

0

−

=

v

f

.

Pierwiastek znajduje się w przedziale

(

)

997

,

0

,

995

,

0

. Badamy znak

( )

v

f

dla

996

,

0

=

v

:

996

,

0

=

v

;

( )

0002887

,

0

=

v

f

.

Pierwiastka szukamy w przedziale

(

)

997

,

0

,

996

,

0

. Badamy znak

( )

v

f

dla

9965

,

0

=

v

:

9965

,

0

=

v

;

( )

0001197

,

0

=

v

f

.

Badając znaki wnioskujemy, że pierwiastek znajduje się w przedziale

(

)

997

,

0

,

9965

,

0

. Badamy znak

( )

v

f

dla

99675

,

0

=

v

:

99675

,

0

=

v

;

( )

0000494

,

0

=

v

f

.

Pierwiastek znajduje się w przedziale

(

)

997

,

0

,

99675

,

0

. Kontynuując postępowanie, znajdujemy pierwiastek z

dowolną dokładnością. Zauważmy, że wartości bezwzględne

( )

v

f

są coraz mniejsze, co oznacza, że kolejne

wartości v coraz mniej różnią się od poszukiwanego pierwiastka równania.
Wyznaczmy przedział, w którym zawarte jest p . Korzystając z (2) otrzymujemy:

12

12 −

=

v

p

.

Dla

99675

,

0

=

v

,

0391

,

0

=

p

.

Dla

997

,

0

=

v

,

0361

,

0

=

p

.

Aby otrzymać p z dokładnością do 4 miejsc po przecinku, trzeba wykonać kolejne iteracje przedstawionego wyżej
algorytmu, nazywanego metodą bisekcji.

15. (7.15) Kredyt jest spłacany w równych ratach w wysokości 1500 zł płatnych na koniec każdego półrocza przez
okres 5 lat. Nominalna stopa oprocentowania wynosi i%. Znajdź wysokość tego oprocentowania wiedząc, że spłata
odsetek w ramach ósmej raty wynosi 206 zł.
Odp.: 0,1009=10,09%.

Rozwiązanie

Wyznaczamy udział spłaty odsetkowej i spłaty kapitałowej w ratach, rozpoczynając postępowanie od ósmej raty.

8 rata

Odsetki: 206.

Niespłacony kapitał (od którego płacimy odsetki):

r

206

.

Kapitał spłacony w ramach raty (rata – odsetki):

1294

206

1500

=

−

.

Kapitał do spłaty (w dwóch ostatnich ratach):

1294

206 −

r

.

J.Marcinkowski Rachunek kredytów

9

9 rata

Niespłacony kapitał:

1294

206 −

r

.

Odsetki:

r

r

r

⋅

−

=

⋅

⎟

⎠

⎞

⎜

⎝

⎛

−

1294

206

1294

206

.

Kapitał spłacony w ramach raty:

(

)

r

r

⋅

+

=

⋅

−

−

1294

1294

1294

206

1500

.

Kapitał do spłaty (w ostatniej racie):

(

)

r

r

r

r

206

2588

1294

1294

1294

1294

206

+

−

⋅

−

=

⋅

+

−

−

.

10 rata

Niespłacony kapitał:

r

r

206

2588

1294

+

−

⋅

−

.

Odsetki:

r

r

r

⋅

⎟

⎠

⎞

⎜

⎝

⎛

+

−

⋅

−

206

2588

1294

.

Spłata kapitałowa + spłata odsetkowa = rata. Odpowiednie równanie przyjmuje postać:

1500

206

2588

1294

206

2588

1294

=

⋅

⎟

⎠

⎞

⎜

⎝

⎛

+

−

⋅

−

+

+

−

⋅

−

r

r

r

r

r

.

Dokonując elementarnych przekształceń otrzymujemy:

0

206

3882

3882

1294

2

=

+

−

⋅

−

⋅

−

r

r

r

,

0

206

3882

3882

1294

2

3

=

−

⋅

+

⋅

+

⋅

r

r

r

.

Pierwiastkami równania są:

050474

,

0

;

9097

,

0

525

,

1

;

9097

,

0

525

,

1

3

2

1

=

−

−

=

+

−

=

r

i

r

i

r

.

Równanie to ma dokładnie jeden pierwiastek dodatni (zob. komentarz 2 do zadania 6.6). Oprocentowanie nominalne
jest równe

%)

09

,

10

(

100948

,

0

050474

,

0

2

2

3

=

⋅

=

⋅ r

.

16. (7.8) Pan Kowalski chce zaciągnąć kredyt w wysokości 10 000 zł spłacany przez okres jednego roku.

W A-banku zaproponowano mu kredyt oprocentowany na 10,85%, przy czym całość odsetek od kredytu należało

spłacić z góry w chwili jego zaciągnięcia, natomiast równe miesięczne raty kapitałowe na końcu każdego miesiąca.

W banku B zaproponowano kredyt oprocentowany na 20%, a równe raty umorzeniowe należało płacić na końcu

każdego miesiąca.
Który z banków daje panu Kowalskiemu atrakcyjniejszy kredyt?
Odp.: Bank A.

Rozwiązanie

Wybór atrakcyjniejszego kredytu sprowadza się do wyboru kredytu o mniejszym rzeczywistym oprocentowaniu.

Bank A

Kapitał: 10 000 PLN.
Kapitał netto: 10 000 – 10 000·0,1085 = 9891,50 PLN.
Rata kapitałowa: 10 000/12 = 833,33 PLN.

Równanie umorzeniowe:

(1)

(

)

(

)

(

)

r

r

r

r

r

⋅

+

−

+

⋅

=

+

+

+

+

=

12

12

12

1

1

1

33

,

833

1

33

,

833

...

1

33

,

833

50

,

9891

,

J.Marcinkowski Rachunek kredytów

10

gdzie r jest oprocentowaniem w skali miesiąca: oprocentowanie nominalne jest r równe

r

⋅

12

.

Bank A

Oprocentowanie rzeczywiste jest równe nominalnej stopie procentowej.

Wyznaczenie r wymaga zastosowania metod numerycznych. Jego dokładna wartość nie jest nam jednak potrzebna,
gdyż naszym celem jest jedynie porównanie atrakcyjności kredytów, a więc stwierdzenie, czy oprocentowanie
rzeczywiste kredytu w banku A jest mniejsze od tegoż oprocentowania w banku B.
Oprocentowanie miesięczne w banku B wynosi

0166

,

0

12

20

,

0

=

. Jeżeli

0166

,

0

<

r

to opłaca się wziąć kredyt w banku A.

W celu porównania wysokości oprocentowania w obu bankach podstawiamy miesięczną stopę procentową
obowiązującą w banku B do równania (1):

(

)

(

)

(

)

61

,

8999

7996

,

10

33

,

833

0166

,

1

0166

,

1

1

0166

,

1

33

,

833

0166

,

0

1

33

,

833

...

0166

,

0

1

33

,

833

12

12

12

=

⋅

=

⋅

−

⋅

=

+

+

+

+

.

Przy spadku oprocentowania r suma bieżących wartości rat umorzeniowych wzrasta. Dla

0166

,

0

=

r

wartość

bieżąca rat umorzeniowych (9149,04 PLN) jest mniejsza od kapitału netto (9891,50 PLN). Oznacza to, ze

0166

,

0

<

r

: kredyt w banku A jest bardziej atrakcyjny.

17. (7.20) Pożyczka jest spłacana za pomocą 10 malejących rat płatnych na końcu każdego roku odpowiednio w
wysokości 20, 19, 18, 17, 16, 15, ....,11 dukatów. Oblicz wysokość odsetek płatnych w piątej racie, jeśli nominalna
stopa procentowa wynosi 10%.
Odp.: 6.

Rozwiązanie

Raty tworzą malejący ciąg arytmetyczny. Rata jest równa sumie spłaty kapitałowej i odsetkowej. Ponieważ
oprocentowanie jest stałe, kapitał do spłaty (a więc i rata odsetkowa) muszą zmniejszać się z raty na ratę o stałą
dodatnią - w naszym przypadku równą 1.

W ostatnie racie spłacamy pozostały do spłaty kapitał oraz odsetki od tego kapitału. Niech

10

K

oznacza kapitał

pozostały do spłaty w ostatniej, dziesiątej racie. Jego wysokość wyznaczamy z równania:

(

)

11

1

,

0

1

10

=

+

⋅

K

,

10

10

=

K

.

Wysokość udzielonej pożyczki jest równa

100

10

10

=

⋅

=

K

.

Po spłacie czterech rat, w piątej racie niespłacony kapitał jest równy

60

10

4

100

=

⋅

−

, a zapłacone odsetki -

6

1

,

0

60

=

⋅

. Łatwo sprawdzić poprawność obliczeń: wysokość raty jest równa sumie raty kapitałowej i odsetkowej,

tj.

16

6

10

=

+

, czyli tyle, ile faktycznie ona wynosi.