1

1

Fale

elektromagnetyc

zne i anteny

ZI - elektronika i

telekomunikacjia

semestr VII

2

2

Prowadzenie fal

Prowadzenie fal

elektromagnetyczn

elektromagnetyczn

ych

ych

3

3

Prowadzenie fal

Prowadzenie fal

elektromagnetycznych

elektromagnetycznych

:

:

- linie transmisyjne TEM

- linie transmisyjne TEM

- falowody (światłowody)

- falowody (światłowody)

4

4

4

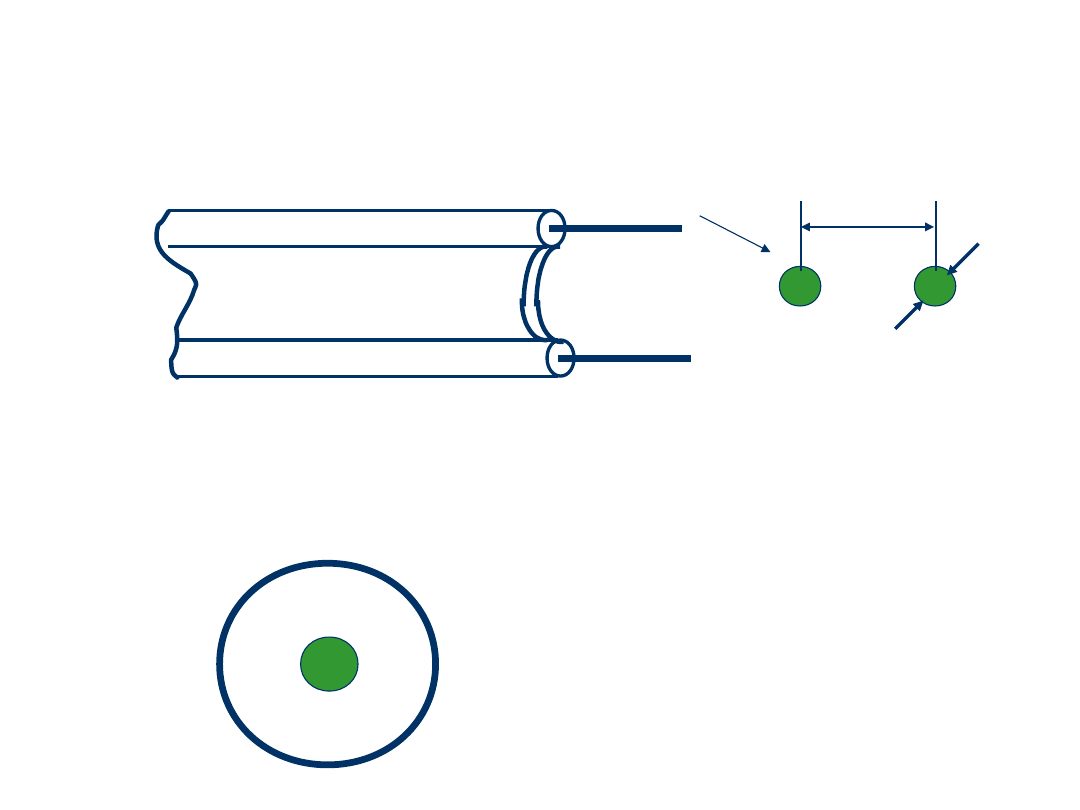
Linia transmisyjna

Linia transmisyjna



Linia symetryczna płaska



Linia współosiowa (koncentryczna)

s

d

d - średnica przewodu
wewnętrznego
D - średnica przewodu
zewnętrznego

5

5

5

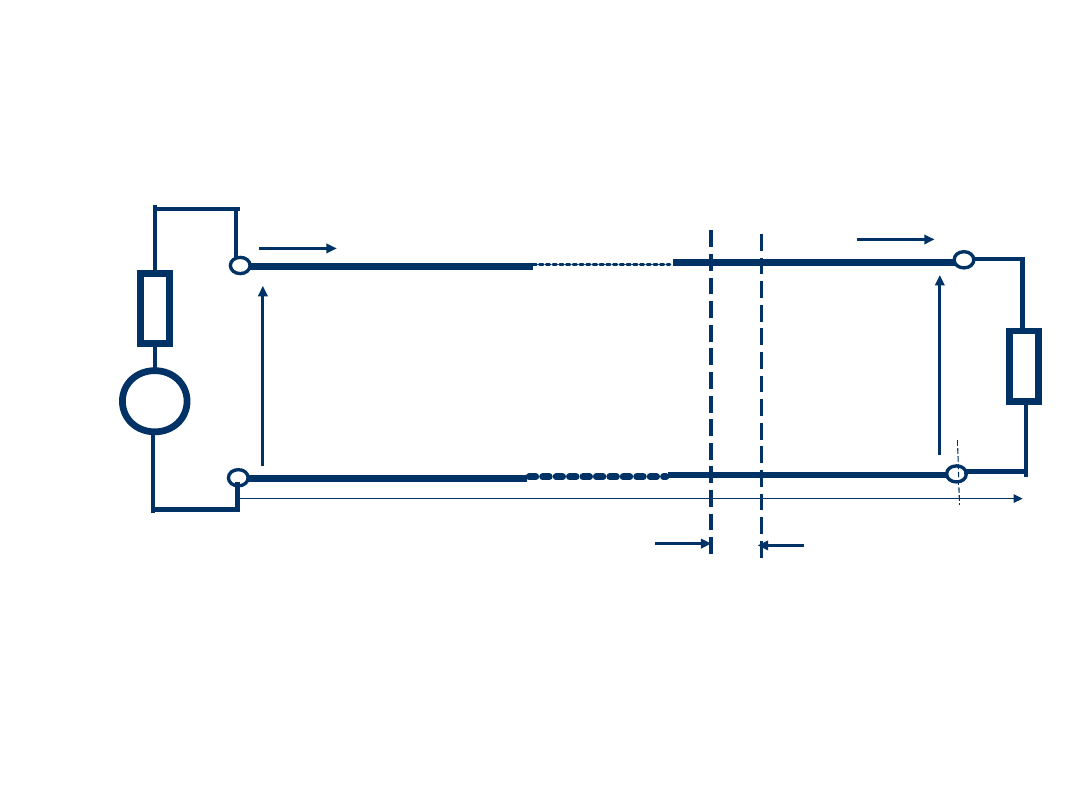
Model linii transmisyjnej

Model linii transmisyjnej

elementarny odcinek linii

z = 0

Z

L

Z

G

U

G

V

we

V

wy

I

we

I

wy

z = L

 z

6

6

6

Model elementarnego odcinka linii

Model elementarnego odcinka linii

L, R, C, G - parametry linii na jednostkę

długości

L z

R z

C z

G z

v(z,t)

v(z+z,t)

i(z,t)

i(z +z,t)

t

t)

i(z,

L

t)

i(z,

R

t

t)

v(z,

t)

z,

v(z

t

t)

i(z,

z

L

t)

i(z,

z

R

t)

v(z,



































0

jeżeli z  0, to:

II prawo Kirchhoffa

:

7

7

7

v(z+z,

t)

L z

R z

C z

G z

v(z,t)

i(z,t)

i(z +z,t)

t

t)

v(z,

C

t)

v(z,

G

t

t)

i(z,

t)

z,

i(z

t

t)

v(z,

z

C

t)

v(z,

z

G

t)

i(z,



































0

jeżeli z  0, to:

I prawo

Kirchhoffa :

8

8

8

Równania telegrafistów dla linii

Równania telegrafistów dla linii

transmisyjnej

transmisyjnej

t

t)

i(z,

L

t)

i(z,

R

z

t)

v(z,

-













t

t)

v(z,

C

t)

v(z,

G

z

t)

i(z,

-













9

9

9

Time-Harmonic Transmission Line

Time-Harmonic Transmission Line

Equation

Equation

V(z)

C)

j

(G

dz

dI(z)

-

I(z)

L)

j

(R

dz

dV(z)

-













only,

coordinate

space

of

functions

are

I(z)

and

V(z)

where

ωt)

exp(j

I(z)

[

Re

t)

i(z,

ωt)

exp(j

V(z)

[

Re

t)

v(z,

:

functions

harmonic

-

time

a

for

phasors

Using

]

]





10

10

10

General Transmission Line Equation

General Transmission Line Equation

The coupled time-harmonic transmission line equation:

C)

j

L)(G

j

R

j

:

where

I(z)

dz

I(z)

d

V(z)

dz

V(z)

d

2

2

2

2

2

2





























(

współczynnik propagacji

przy czym:   0 i   0.

11

11

11

Rozwiązanie ogólne

C

j

G

L

j

R

Z

e

I

e

I

(z)

I

(z)

I

I(z)

e

V

e

V

(z)

V

(z)

V

V(z)

0

z

m

z

-

m

-

z

m

z

-

m

-















































Iloraz napięcia i prądu fali padającej i/lub ze
znakiem ujemnym napięcia i prądu fali odbitej
nazywamy impedancją falową linii:

12

12

12

Linia bezstratna

Linia bezstratna

C

L

Z

:

impedance

stic

characteri

LC

1

u

:

velocity

phase

LC

j

:

constant

n

propagatio

0

G

and

0

R

0

p





















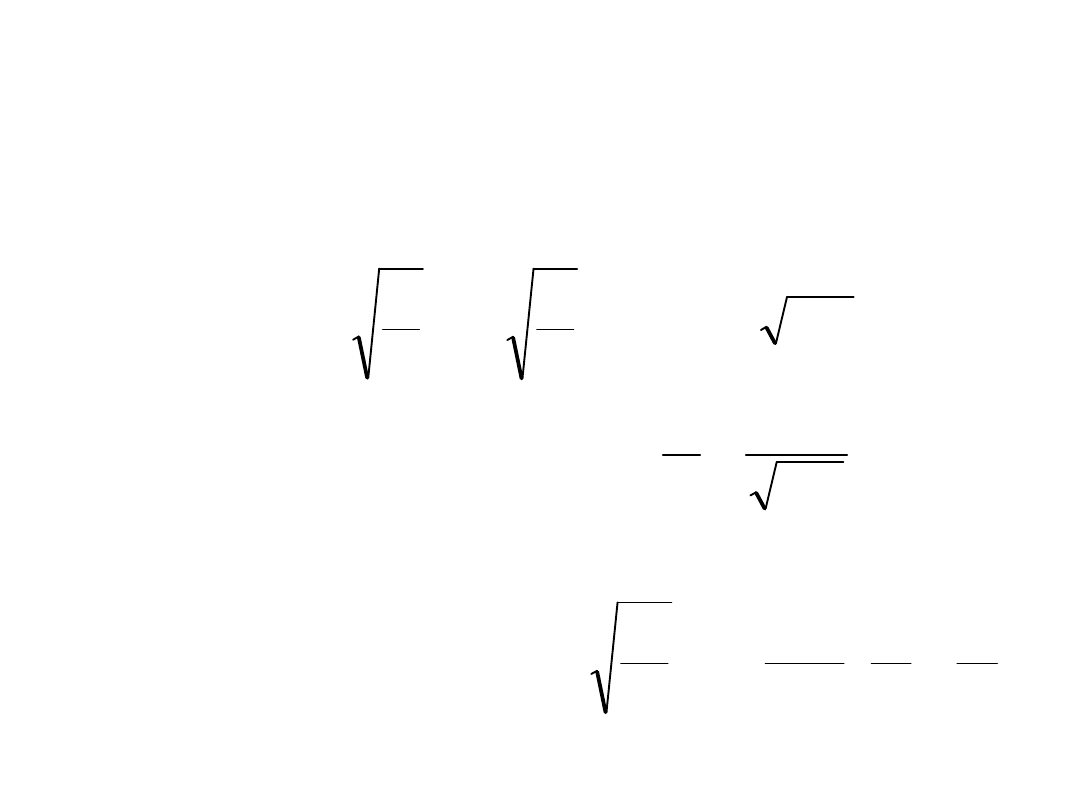
13

13

13

Linia o małych stratach

Linia o małych stratach

]

)

C

G

L

R

(

2j

1

1

[

C

L

Z

:

impedance

stic

characteri

LC

1

u

:

velocity

phase

LC

,

)

C

L

G

L

C

R

(

j

:

constant

n

propagatio

C

G

,

L

R

0

p

















































5

0.

14

14

14

Linia niezniekształcająca

Linia niezniekształcająca

C

L

Z

:

impedance

stic

characteri

LC

1

u

:

velocity

phase

j

R

(

L

C

:

constant

n

propagatio

C

G

L

R

0

p





















)

L

15

15

15

Impedancje charakterystyczne linii

Impedancje charakterystyczne linii

,

d

D

ln

60

Z

,

d

2s

ln

120

Z

r

0

r

0









s

d

Linia symetryczna płaska:

Linia współosiowa:

16

16

16

Linia o skończonej długości zakończona

Linia o skończonej długości zakończona

impedancją Z

impedancją Z

L

L

Napięcie i prąd na końcu

z=l

linii są

równe:

Rozwiązując ze względu na amplitudy
napięcia fali padającej i powrotnej:

l

l

l

l









e

Z

V

e

Z

V

I

e

V

e

V

V

m

m

L

m

m

L

0

0





















l

l



















e

)

Z

I

(V

.

V

e

)

Z

I

(V

.

V

L

L

m

L

L

m

0

0

5

0

5

0

]

e

)

Z

(Z

e

)

Z

(Z

[

Z

I

I(z)

]

e

)

Z

(Z

e

)

Z

(Z

[

I

V(z)

)

(

L

)

(

L

L

)

(

L

)

(

L

L

z

l

z

l

z

l

z

l





































0

0

0

0

0

2

2

z

z

z

z









e

I

e

I

I(z)

e

V

e

V

V(z)

m

m

m

m





















17

17

17

Współrzędne l i z występują w kombinacji (l
- z), zatem wprowadzając nową zmienną z’
= l - z otrzymamy:

]

e

)

Z

(Z

e

)

Z

(Z

[

Z

I

)

I(z'

]

e

)

Z

(Z

e

)

Z

(Z

[

I

)

V(z'

'

L

'

L

L

'

L

'

L

L

z

z

z

z





























0

0

0

0

0

2

2

Przy czym odległość z’ jest mierzona jako
dodatnia od obciążenia do źródła.
Wykorzystując definicje funkcji
hiperbolicznych:

otrzymujemy napięcie i prąd w dowolnym
punkcie z’:

)

'

sinh(

e

e

),

'

cosh(

e

e

z'

z'

z'

z'

z

z













2

2













]

)

z'

cosh(

Z

)

z'

sinh(

Z

[

Z

I

)

I(z'

]

)

z'

sinh(

Z

)

z'

cosh(

Z

[

I

)

V(z'

L

L

L

L









0

0

0









18

18

18

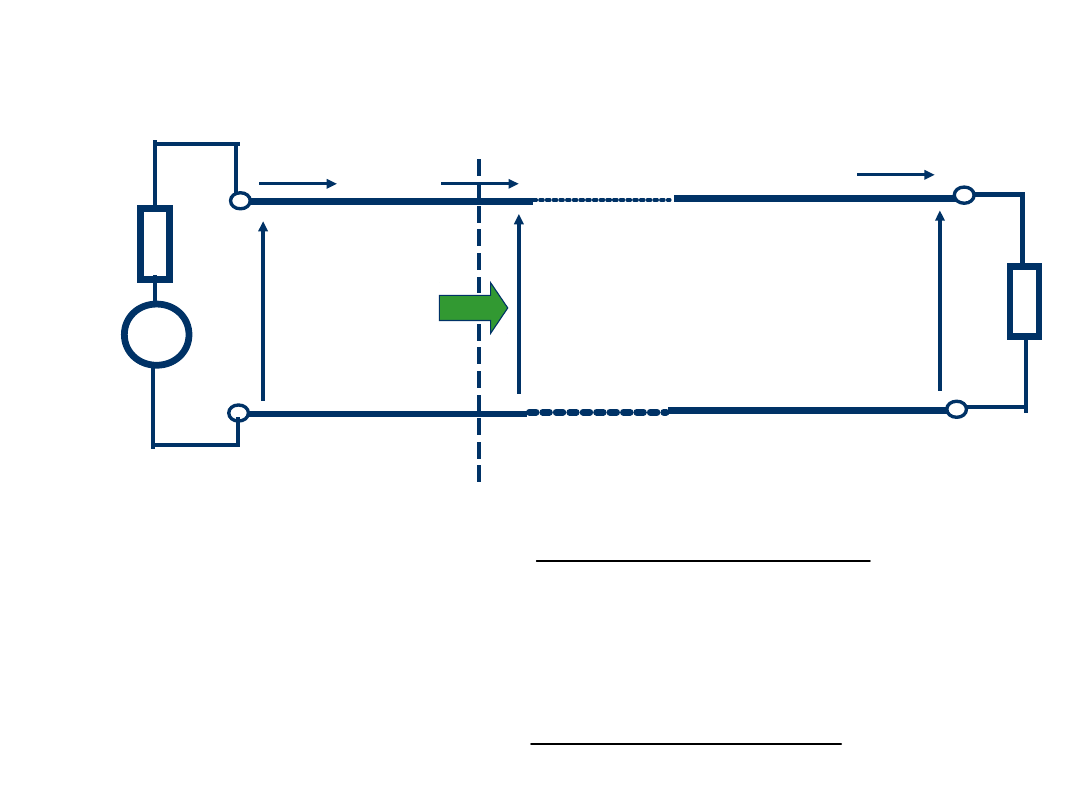
Iloraz V(z’)/I(z’) jest impedancją linii
widzianą w punkcie z’ od obciążenia i w
kierunku obciążenia:

z’ = l

Z

L

Z

G

U

G

V

we

V

wy

I

we

I

wy

z’ =
0

z’

V(z’)

I(z’)

)

z'

tanh(

Z

Z

)

z'

tanh(

Z

Z

Z

)

Z(z'

L

L











0

0

0

)

tanh(

Z

Z

)

tanh(

Z

Z

Z

Z

L

L

we

l

l











0

0

0

oraz impedancja wejściowa linii:

19

19

19

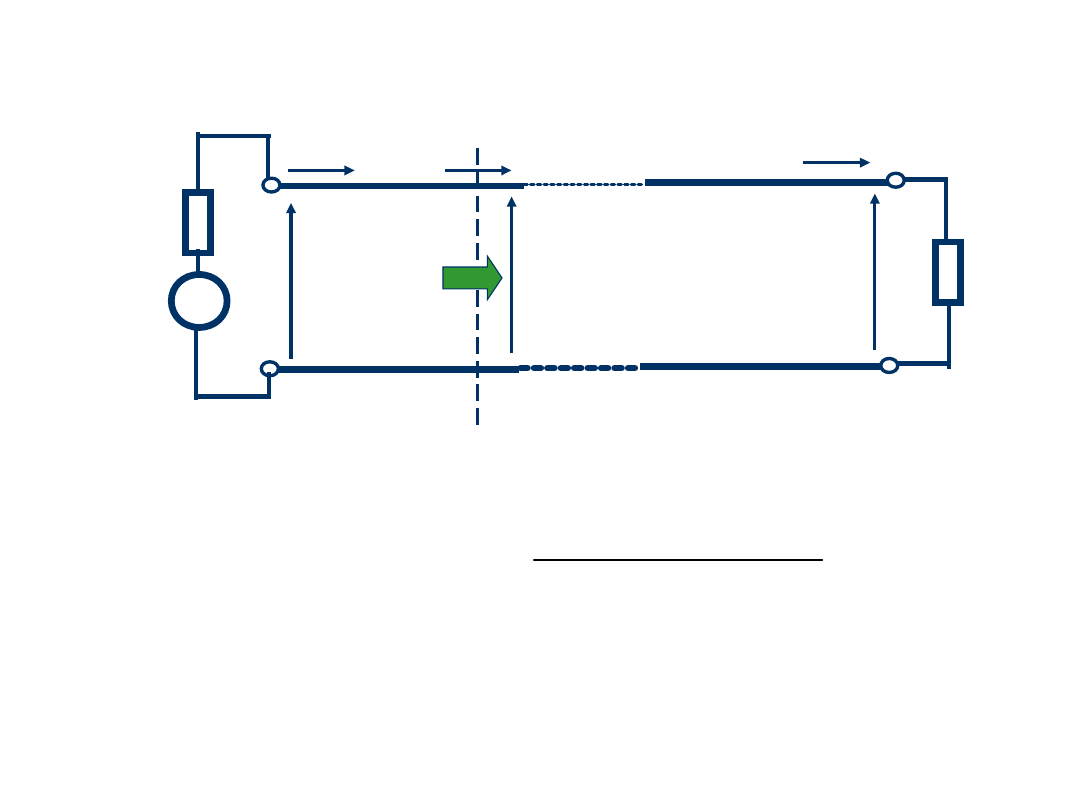
Przypadek dopasowania obciążenia do

Przypadek dopasowania obciążenia do

linii

linii

Z

Z

L

L

= Z

= Z

0

0

Impedancja linii w dowolnym punkcie:

oraz napięcie i prąd:

0

0

0

0

0

0

Z

)

z'

tanh(

Z

Z

)

z'

tanh(

Z

Z

Z

)

Z(z'













z

z

l

z

l

z

l

z

z

l

z

l

z

l

































































e

I

e

)

e

(I

]

e

)

Z

(Z

e

)

Z

(Z

[

Z

I

I(z)

e

V

e

)

e

Z

(I

]

e

)

Z

(Z

e

)

Z

(Z

[

I

V(z)

we

L

)

(

L

)

(

L

L

we

L

)

(

L

)

(

L

L

0

0

0

0

0

0

2

2

zatem w linii występują tylko składowe fal
pradu i napięcia transmitowane od źródła
do obciążenia - brak jest fal powrotnych.
Cała energia dostarczona ze źródła jest
wydzielana w obciążeniu.

20

20

20

Linia transmisyjna bezstratna jako

Linia transmisyjna bezstratna jako

element obwodowy

element obwodowy

z’ =
l

Z

L

Z

G

U

G

V

we

V

wy

I

we

I

wy

z’=
0

z’

V(z’
)

I(z’)

)

tg(

Z

j

R

)

tg(

R

j

Z

R

Z

L

L

we

l

l











0

0

0

Impedancja wejściowa jest równa:

przy czym wykorzystano tu znaną
zależność:

tanh(jx) = j tg(x)

21

21

21

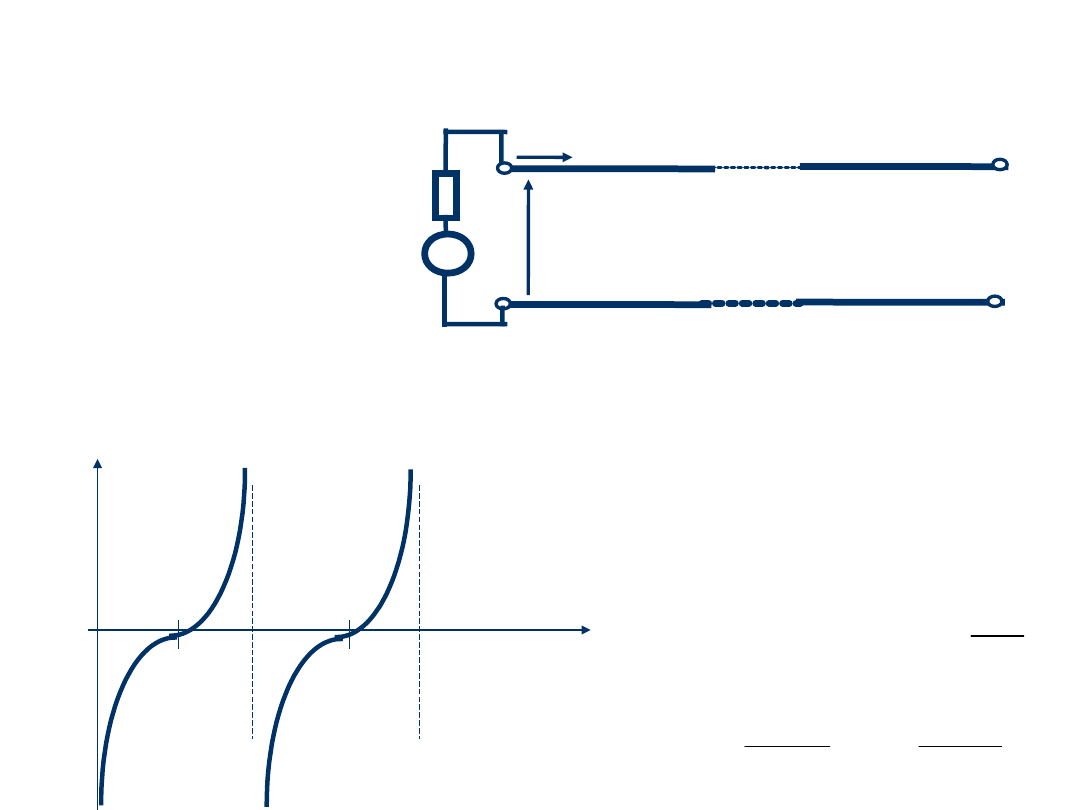
Przypadek szczególny 1

Przypadek szczególny 1

z’ =
l

Z

G

U

G

V

we

I

we

z’=
0

)

cot(

jR

jX

Z

o

we

o

we

l



0







Impedancja
wejściowa jest
równa:

1. Linia rozwarta
na końcu, Z

L

=:



pojemnościow

y

/4

3/
4

/2



l

X

we o

indukcyjny

Dla linii bardzo krótkiej:
l << 1, 2l <<  , l <<

0.16  ,

z

o

we

o

we

C

j

C

j

R

j

jX

Z







1

1

0















l

l

22

22

22

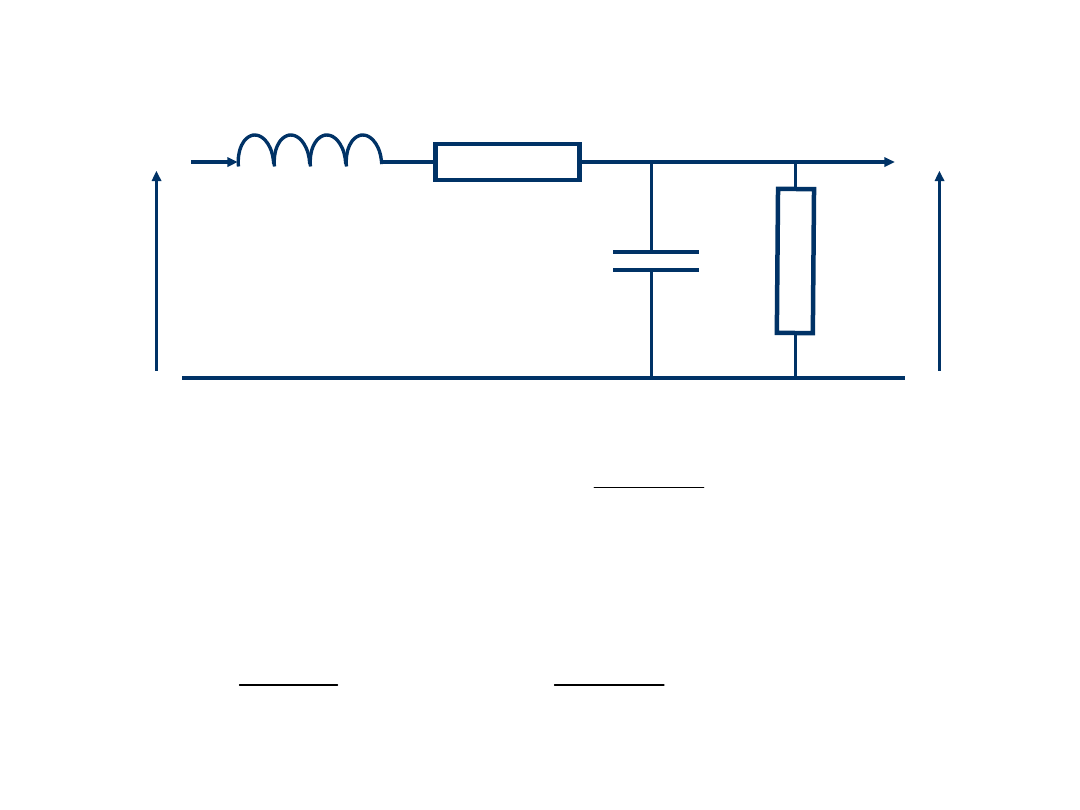
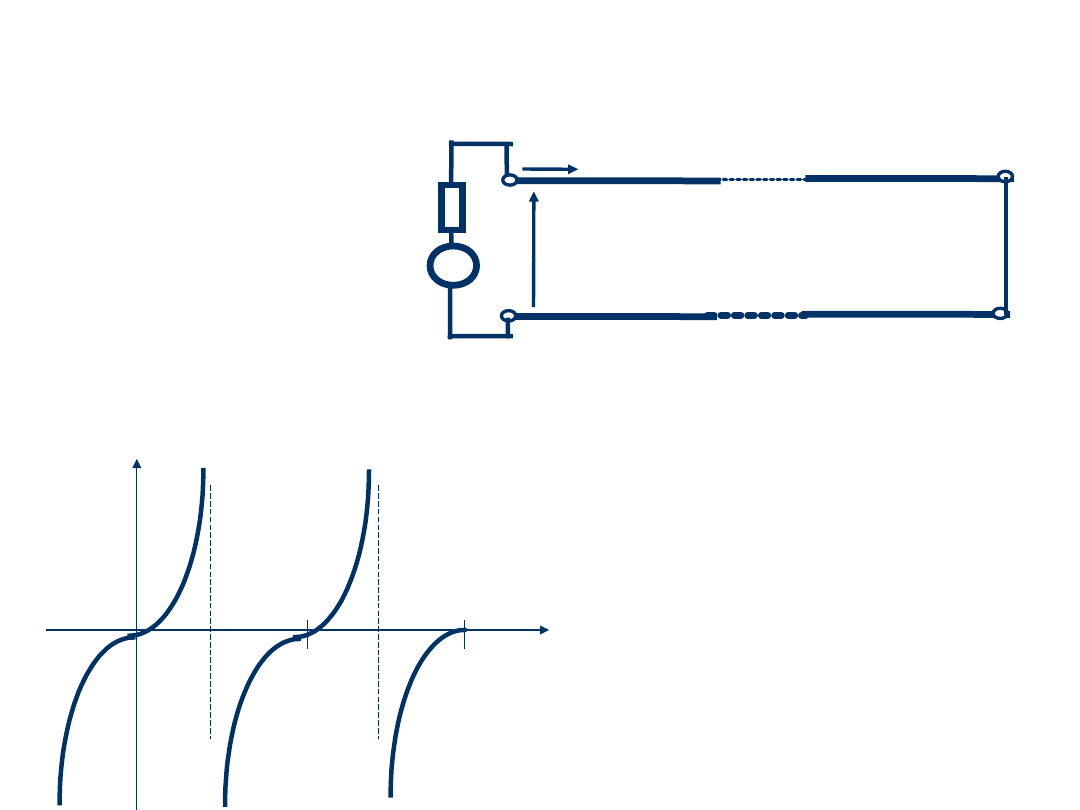
Przypadek szczególny 2

Przypadek szczególny 2

)

tg(

jR

jX

Z

z

we

z

we

l



0





Impedancja
wejściowa jest
równa:

2. Linia zwarta na
końcu, Z

L

=0:



Dla linii bardzo krótkiej:
l << 1, 2l <<  , l <<

0.16  ,

z

z

we

z

we

L

j

L

j

jR

jX

Z

















l

l

0

z’ =
l

Z

G

U

G

V

we

I

we

z’=
0

pojemnościow

y

/4

3/
4

/2



l

X

we o

indukcyjny

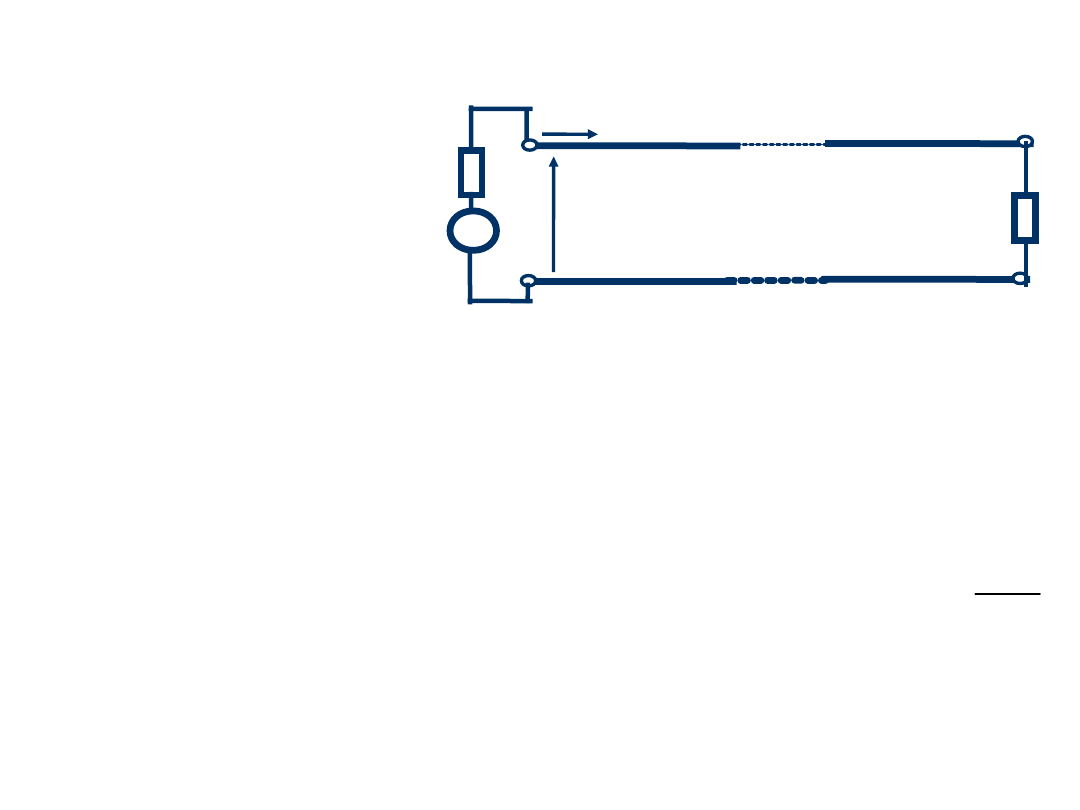
23

23

23

Przypadek szczególny 3

Przypadek szczególny 3

L

t

we

Z

R

Z

2
0



Impedancja wejściowa jest

równa:

tzn. na wejściu linii jest widziana

impedancja proporcjonalna do

odwrotności impedancji

obciążenia Z

L

.

3. Transformator
ćwierćfalowy,
l =  /4:



Dla linii o długości l = /4 lub nieparzystej

wielokrotności /4 mamy:

l = ( 2/ ).( 2n - 1)./4 = ( 2n -

1 )./2,
tg ( l ) = tg [ ( 2n - 1) /2 ]  



z’ =
l

Z

G

U

G

V

we

I

we

z’=
0

Z

L

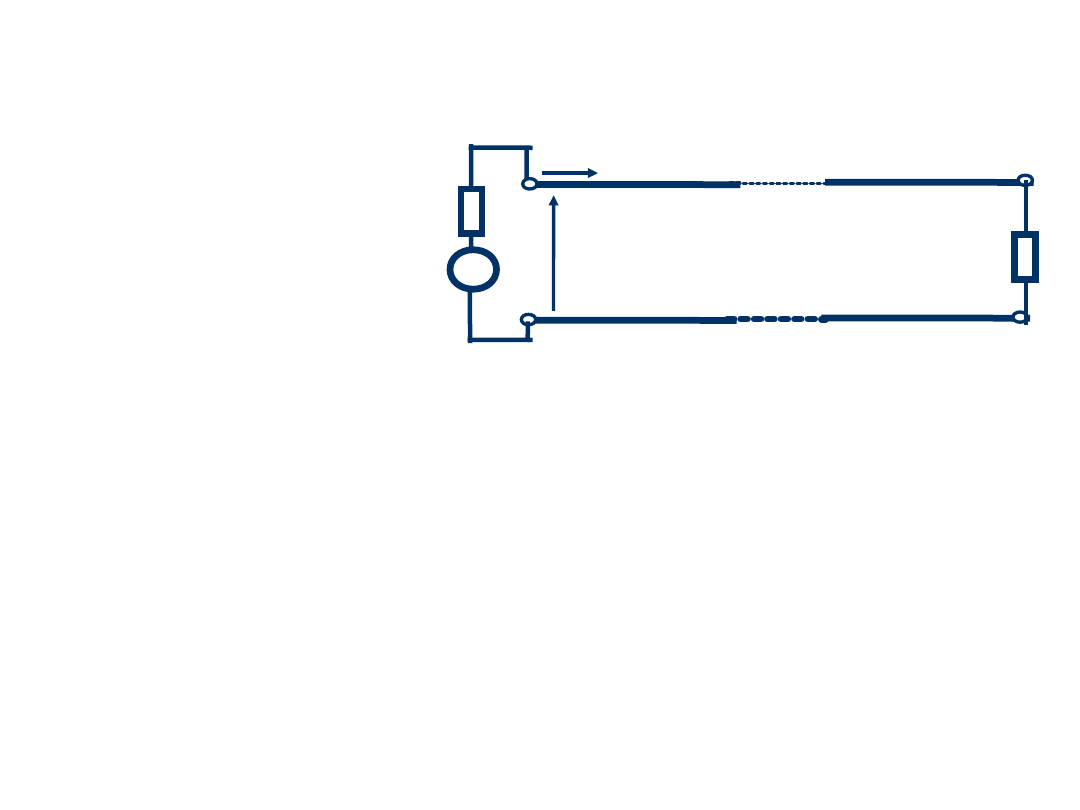
24

24

24

Przypadek szczególny 4

Przypadek szczególny 4

L

.

we

Z

Z



5

0

Impedancja wejściowa jest równa:

tzn. na wejściu linii jest widziana impedancja
obciążenia Z

L

.

4. Sekcja półfalowa,
l =  /2:



Dla linii o długości l = /2 lub

wielokrotności /2 mamy:

l = ( 2/ ).n/2 = n ,
tg ( l ) = 0

z’ =
l

Z

G

U

G

V

we

I

we

z’=
0

Z

L

25

25

25

Doświadczalne wyznaczanie

Doświadczalne wyznaczanie

parametrów linii

parametrów linii

)

Z

Z

arctanh

Z

Z

Z

o

we

z

we

z

we

o

we

1

-

(m

)

(

l

1

0











Dla linii o długości l doświadczalnie
wyznacza się impedancje wejściowe dla
dwóch przypadków:

1. Rozwarcia na wyjściu:

2. Zwarcia na wyjściu:

wtedy:

)

tanh(

Z

Z

)

coth(

Z

Z

z

we

o

we

l

l





0

0





26

26

26

Linia o skończonej długości zakończona

Linia o skończonej długości zakończona

impedancją Z

impedancją Z

L

L

Napięcie w dowolnym punkcie z’ można
zapisać następująco:

Przy czym



jest tzw.

napięciowym

współczynnikiem odbicia od impedancji
obciążenia

linii:

]

e

[

e

)

Z

(Z

I

]

e

Z

Z

Z

Z

[

e

)

Z

(Z

I

]

e

)

Z

(Z

e

)

Z

(Z

[

I

)

V(z'

'

'

L

L

'

L

L

'

L

L

'

L

'

L

L

z

z

z

z

z

z















2

0

2

0

0

0

0

0

1

2

1

2

2











































j

e

Z

Z

Z

Z

I

I

V

V

L

L

m

m

m

m























0

0

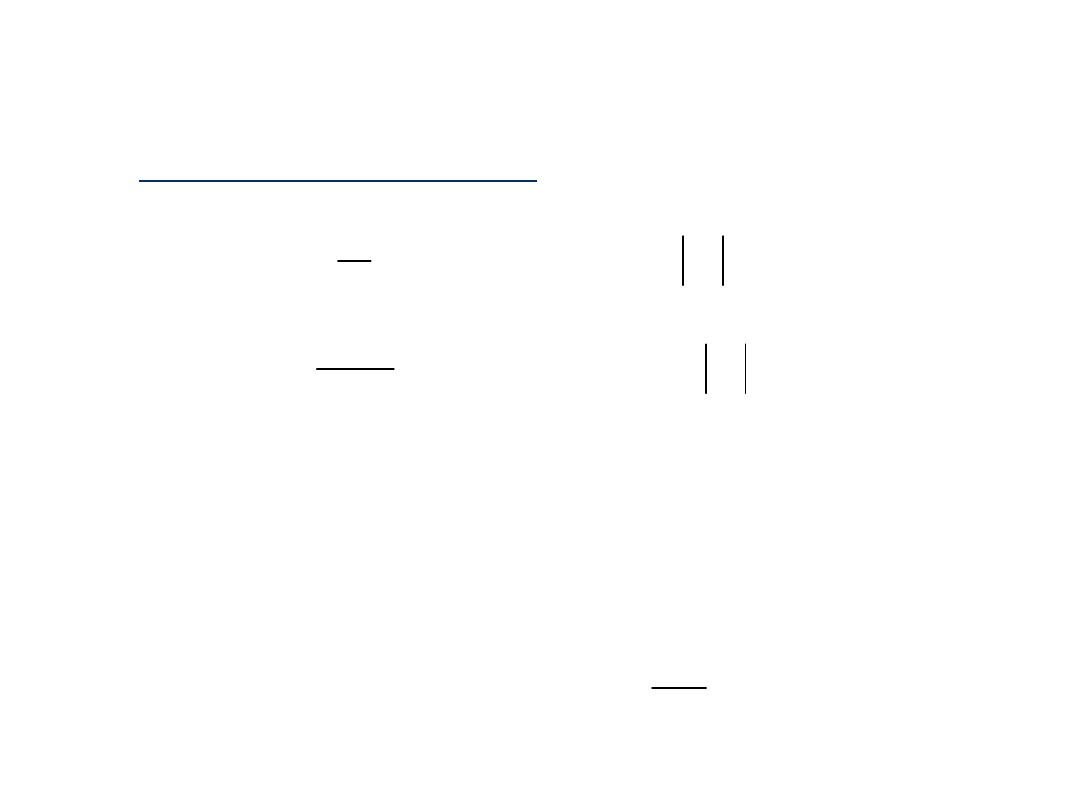
27

27

27

Linia o skończonej długości zakończona

Linia o skończonej długości zakończona

impedancją Z

impedancją Z

L

L

Dla linii bezstratnej  = j :

Wskazy napięcia i prądu wzdłuż linii
można przedstawić również w postaci:

]

[

)

(

)

(

]

[

)

(

)

(

)

'

(

'

L

L

)

'

(

'

L

L

e

e

R

Z

R

I

z'

I

e

e

R

Z

I

z'

V

z

j

z

j

z

j

z

j





















2

0

0

2

0

1

2

1

2

















)

z'

sin(

R

V

)

z'

cos(

I

)

I(z'

)

z'

sin(

R

I

)

z'

cos(

V

)

V(z'

L

L

L

L









0

0

j

j









28

28

28

Moduły napięcia i prądu w linii wykazują w
stałych punktach minima i maksima,
tworząc tzw. falę stojącą, np. dla obciążenia
rzeczywistego Z

L

= R

L

:

Moduł wartości maksymalnej napięcia
występuje dla współrzędnej z’= z’

max

spełniającej warunek:

)

z'

(

sin

R

R

)

z'

(

cos

I

)

I(z'

)

z'

(

sin

R

R

)

z'

(

cos

V

)

V(z'

L

L

L

L









2

2

0

2

2

2

0

2

































1

2







)

'

j(

max

e

z







natomiast moduł wartości minimalnej
występuje dla współrzędnej z’= z’

min

spełniającej warunek:

1

2







)

'

j(

max

e

z







29

29

29

Wartości te wynoszą:

Iloraz modułów maksymalnej i
minimalnej wartości napięcia
w linii nazywamy

współczynnikiem fali stojącej
S

(SWR - Standing Wave Ratio):

]

[

)

(

]

[

)

(





















1

2

1

2

0

0

'

L

L

min

'

L

L

max

e

R

Z

I

V

e

R

Z

I

V

z

j

z

j













1

1

min

max

V

V

S

Moduł współczynnika odbicia  jako

funkcja współczynnika S:
Przypadki szczególne:
 = 0 , S = 1 : Z

L

= Z

0

(dopasowanie)
 = -1, S   : Z

L

= 0 (zwarcie

linii)
 = +1, S   : Z

L

  (rozwarcie

linii)

1

1









S

S

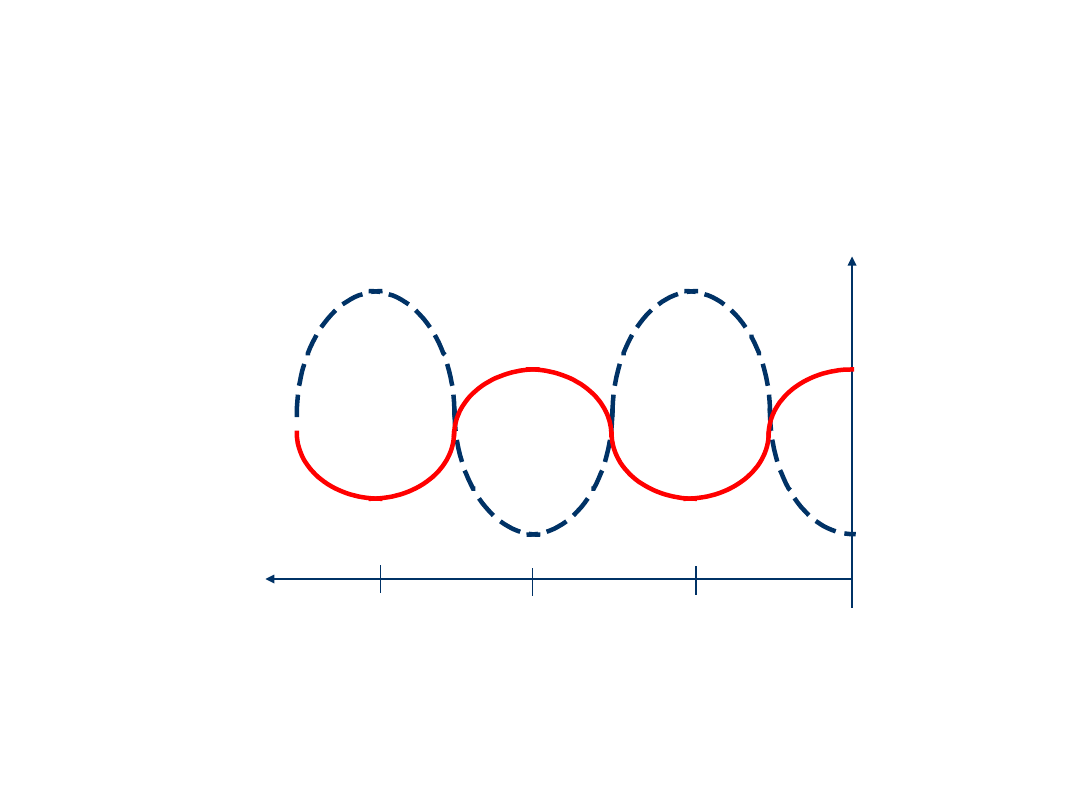
30

30

30

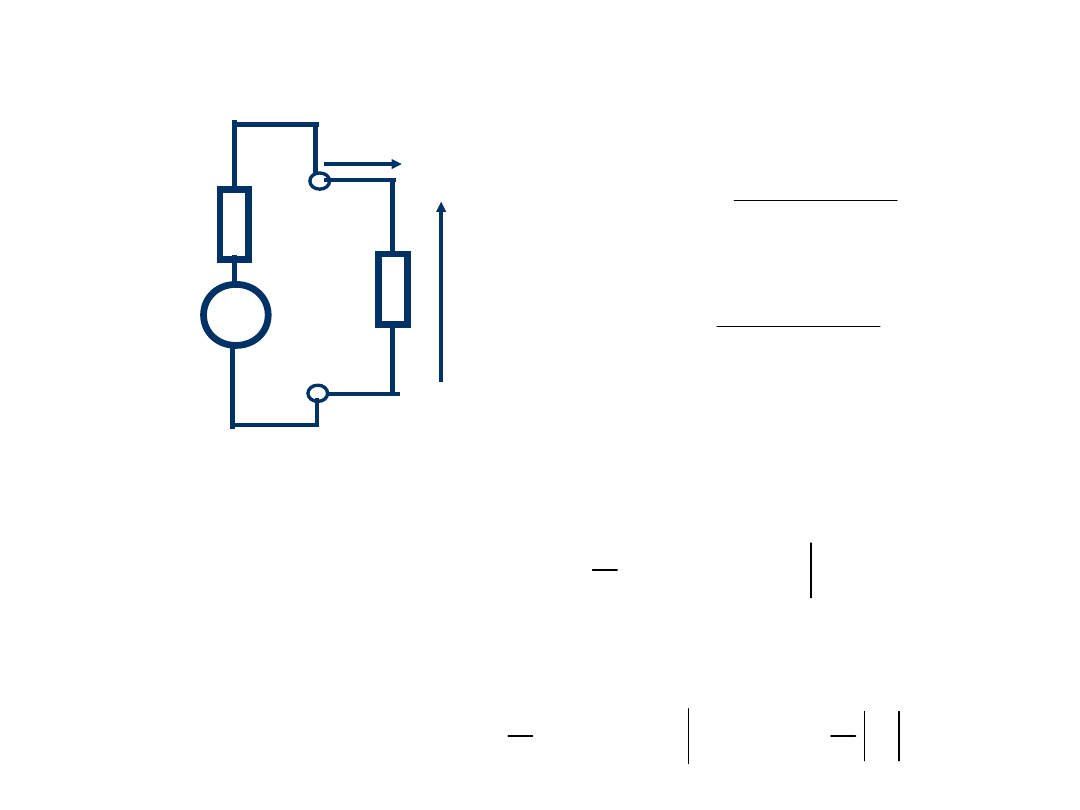
Moduły napięcia i prądu (obwiednie)

fali częściowo stojącej w linii

/4

3/
4

/2

z’

|

V(z’)

|

|

I(z’)|

0

31

31

31

Obwód równoważny linii w punkcie

Obwód równoważny linii w punkcie

zasilania z generatora z = 0

zasilania z generatora z = 0

Średnia moc dostarczona z generatora:

G

we

G

we

G

G

we

we

we

Z

Z

U

I

U

Z

Z

Z

V









Z

G

U

G

Z

w

e

V

we

I

we

l

z

z







'

,

*
we

we

śr

]

I

Re[V

P

0

2

1

Średnia moc dostarczona do obciążenia:

L

L

'

,

*

L

L

śr

R

I

]

I

Re[V

P

2

0

2

1

2

1







 z

l

z

32

32

32

Zadanie 10

Zadanie 10

Generator sinusoidalny o rezystancji
wewnętrznej 1 i napięciu U

G

(t)=0.3 cos(2

10

8

t) V zasila linię transmisyjną bezstratną o

impedancji charakterystycznej 50  . Linia

ma długość 4 m a prędkość propagacji fali w
linii wynosi 2.5E8 m/s. Dla przypadku
dopasowania obciążenia do linii należy
obliczyć:

A) wartości chwilowe napięcia i prądu w linii w

jej dowolnym punkcie,

B) wartości chwilowe prądu i napięcia w

obciążeniu,

C) średnią moc dostarczoną do obciążenia.

33

33

Elementy techniki

Elementy techniki

mikrofalowej

mikrofalowej

34

34

34

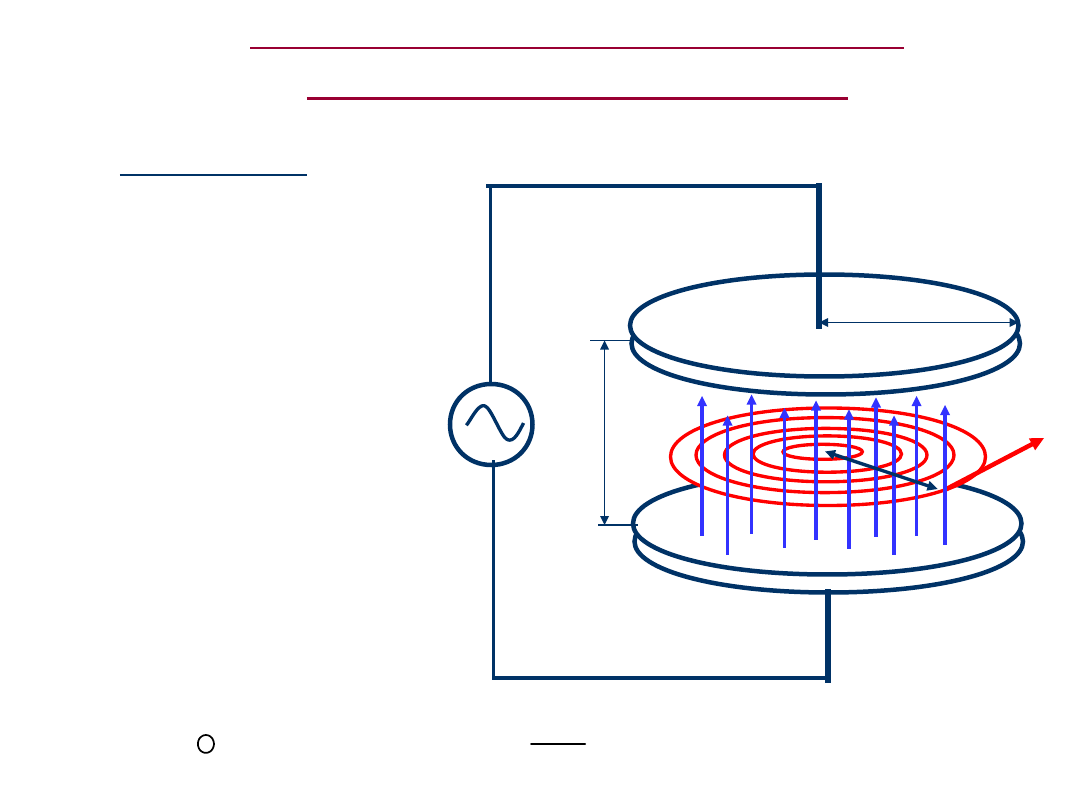
Pole elektromagnetyczne w

przestrzeni zamkniętej

Kondensator przy wielkich
częstotliwościach

Przesłanki:
Pole E wewnątrz
kondensatora jest
sinusoidalnie
zmienne w czasie
E = E

0

e

j

, i

równomiernie
rozłożone w
przestrzeni
pomiędzy płytami.

Zgodnie z prawem
Maxwella powstaje
całka
krzywoliniowa
pola B:

ds

)

dt

dE

(J

dl

B















C

A





B

E

h

a

CC

C

1

CC

S

1

CC

r

35

35

35

Ponieważ prąd przewodzenia jest równy 0, zatem
równanie to upraszcza się do postaci:

ds

dt

dE

dl

B











1

1

C

S

2

c

1

Przy czym C

1

jest obwodem okręgu pola B o

promieniu

r

a S

1

jest powierzchnią tego okręgu. Z

powyższego równania otrzymujemy:

t

j

0

2

e

2







E

c

r

j

B

Pole B wynikające ze zmiennego w czasie pola E jest
również sinusoidalną funkcją czasu i zależy od
promienia r. Zatem również pole E zależy od promienia
r, a to jest sprzeczne z pierwotnym założeniem. Pole E
można przedstawić w postaci:

E = E

1

+ E

2

przy czym E

1

jest polem równomiernym E

1

= E

0

e

j t



f®, natmiast jest poprawką wynikającą z
nierównomiernego pola B.

36

36

36

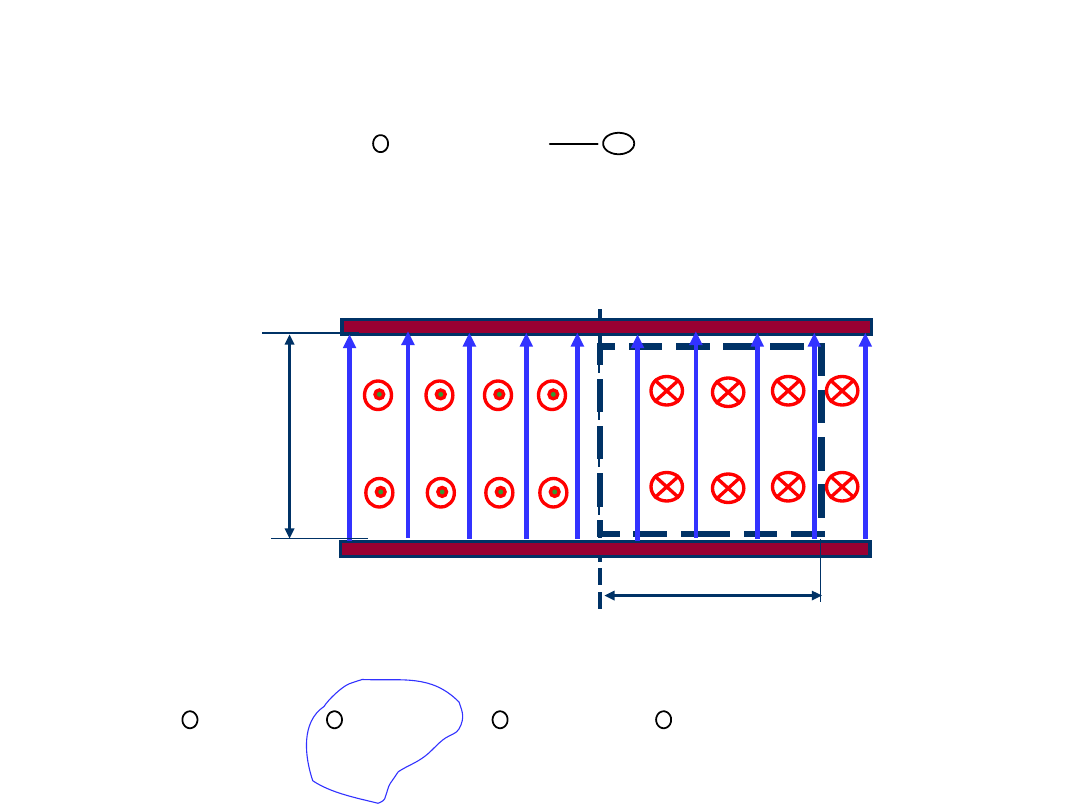
Poprawka E

2

zależy od promienia r i jest równa

E

2

(r=0) = 0. Można ją wyznaczyć z prawa Faraday’a:

ds

B

t

dl

E

















2

2

S

C

przy czym C

2

jest obwodem prostokąta a S

2

jest jego

powierzchnią , zgodnie z poniższym rysunkiem:

Całka po lewej stronie:

h

r

2

C

2

C

C

2

1

C

2

2

2

2

)

(

E

dl

E

dl

E

dl

E

dl

E



























C

C

2

C

S

2

r

h

=
0

37

37

37

Po przekształceniach otrzymujemy:

przy czym C

2

jest obwodem prostokąta a S

2

jest jego

powierzchnią , zgodnie z poniższym rysunkiem:

Nasze poprawione pole E nie jest już równomierne,
zatem również pole B jest sumą dwóch składników: B
= B

1

+ B

2

, przy czym składnik B

2

jest poprawką

wytworzoną przez pole E

2

. Kontynując to

rozumowanie otrzymujemy ostatecznie:

t

j

0

2

2

2

2

1

e

c

r

4

1

1













E

)

(

E

E

E

- a

a

E

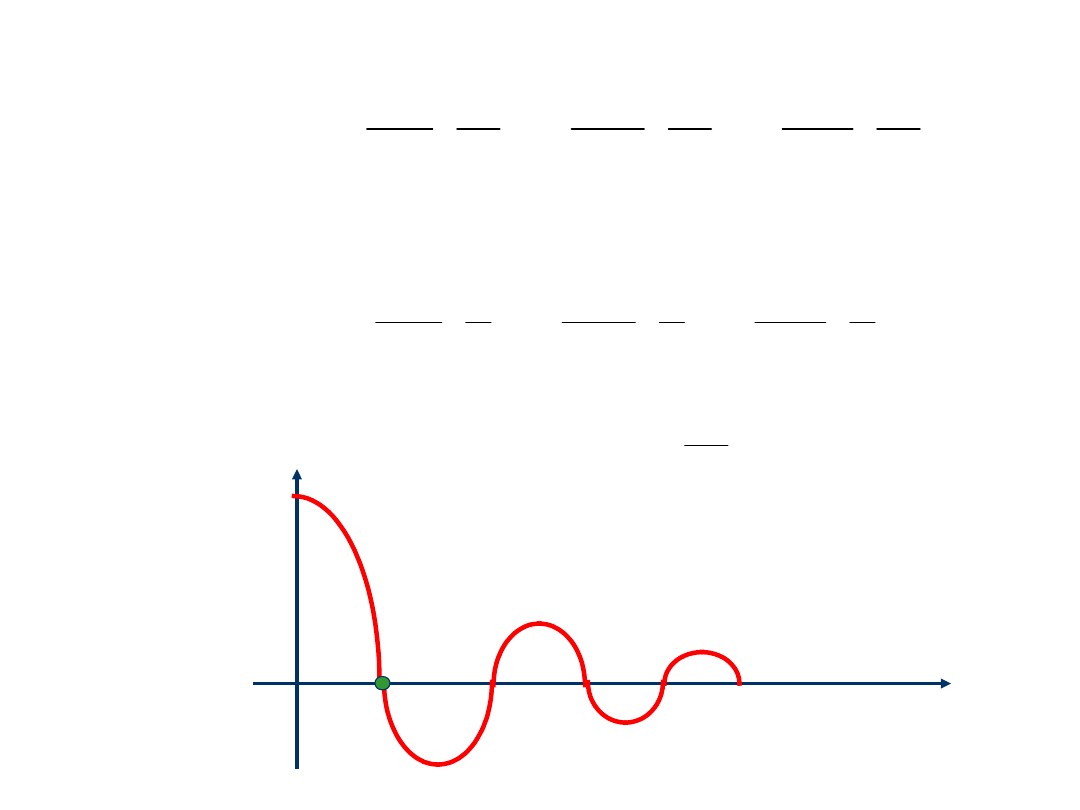
38

38

38

Po przekształceniach otrzymujemy:

przy czym wyraz w nawiasie jest funkcją specjalną
Bessela zerowego rzędu:

...]

c

2

r

!)

3

(

1

c

2

r

!)

2

(

1

c

2

r

!)

1

(

1

1

[

e

6

2

4

2

2

2

t

j

0













 













 













 







E

E

...

2

x

!)

3

(

1

2

x

!)

2

(

1

2

x

!)

1

(

1

1

(x)

6

2

4

2

2

2

0















































J











 





c

r

e

0

t

j

0

J

E

E

J

0

(x)

1

2.405

x=r/c

39

39

39

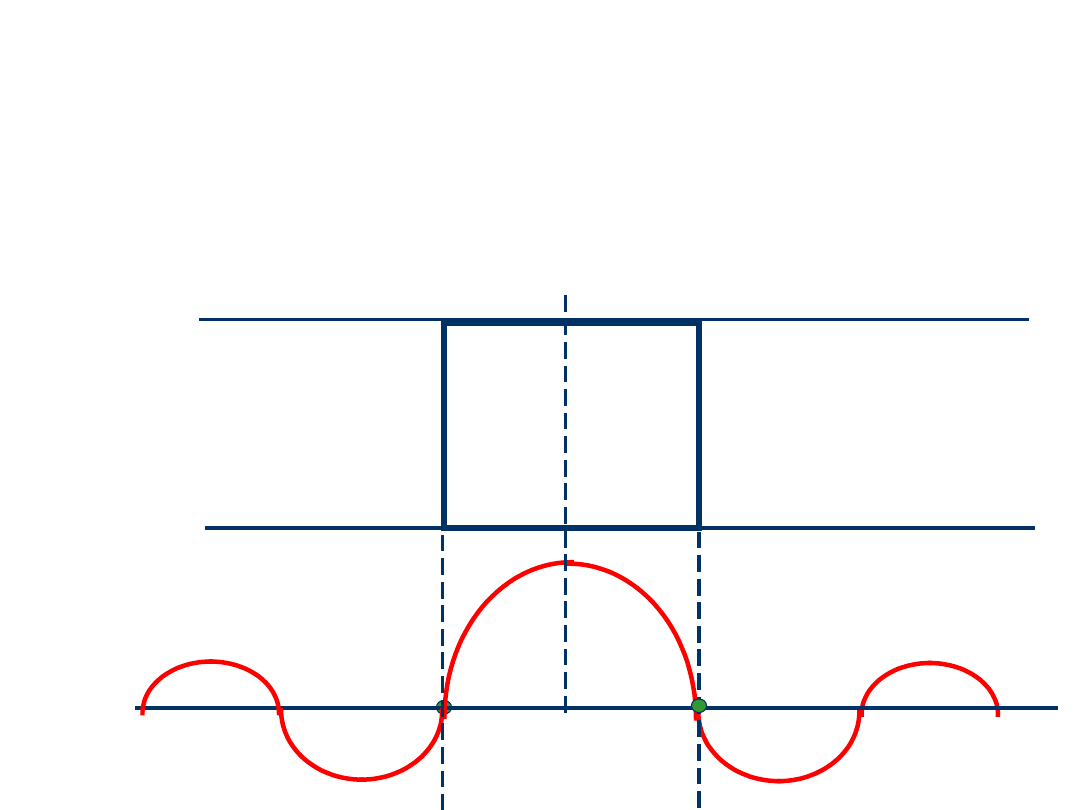
Pole elektryczne w kondensatorze przy bardzo dużych
częstotliwościach zależy od położenia względem środka
kondensatora, czyli od promienia r.
Jeżeli  = 0, to J

0

(0) = 1 i pole E jest równomierne,

natomiast jeżeli promień r’ i częstotliwość ’ spełniają

warunek (’ r’)/c = 2.405

to pole E = 0. Zatem rozkład pola nie zmieni się, jeżeli
kondensator zamkniemy ściankami metalowymi dla r’.

r’=2.405c/’

wnęka

mikrofalowa

40

40

40

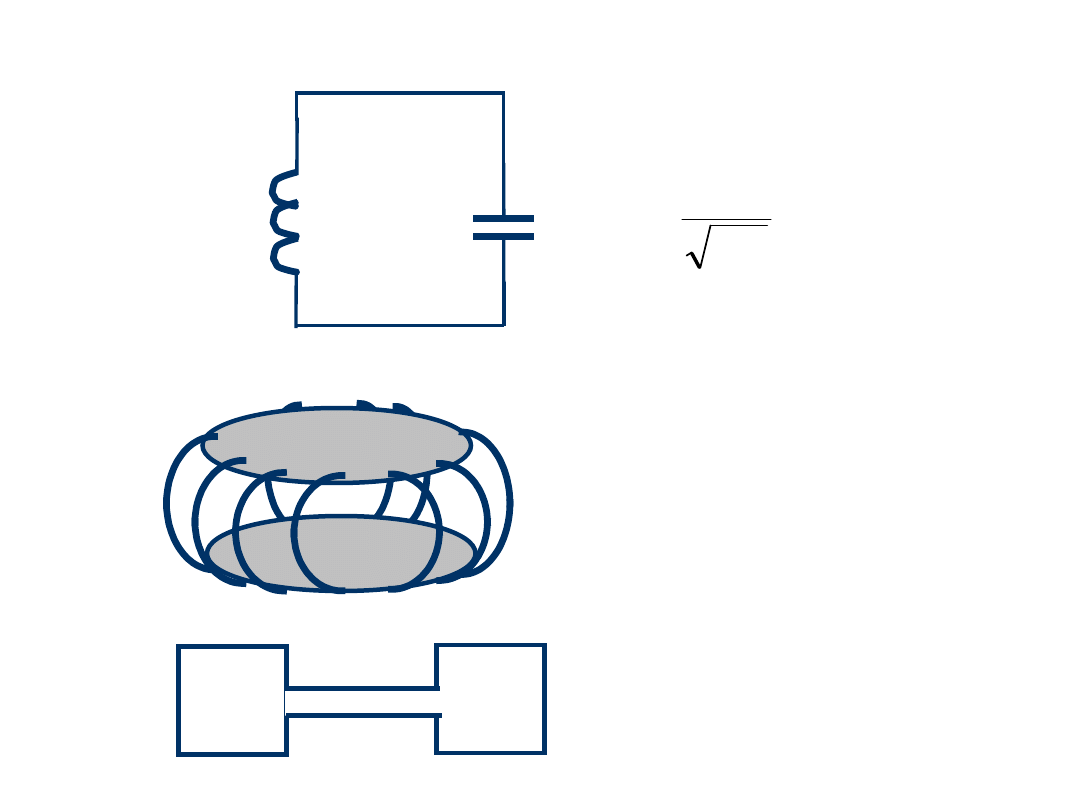
Wnęka mikrofalowa jest obwodem rezonansowym:

Zwiększenie częstotliwości
rezonansowej uzyskuje się np.
przez zmniejszenie L, tzn.
zmniejszenie liczby zwojów do
jednego, lub połączenie
równoległe L.
W ten sposób otrzymujemy
wnękę mikrofalową w roli
obwodu rezonansowego.
Dobroć takiego obwodu dla
częstotliwości mikrofalowych
jest rzędu 100 000 -
nieosiągalna przy użyciu
kondensatorów i cewek
skupionych.

L

C

LC

1

0





41

41

41

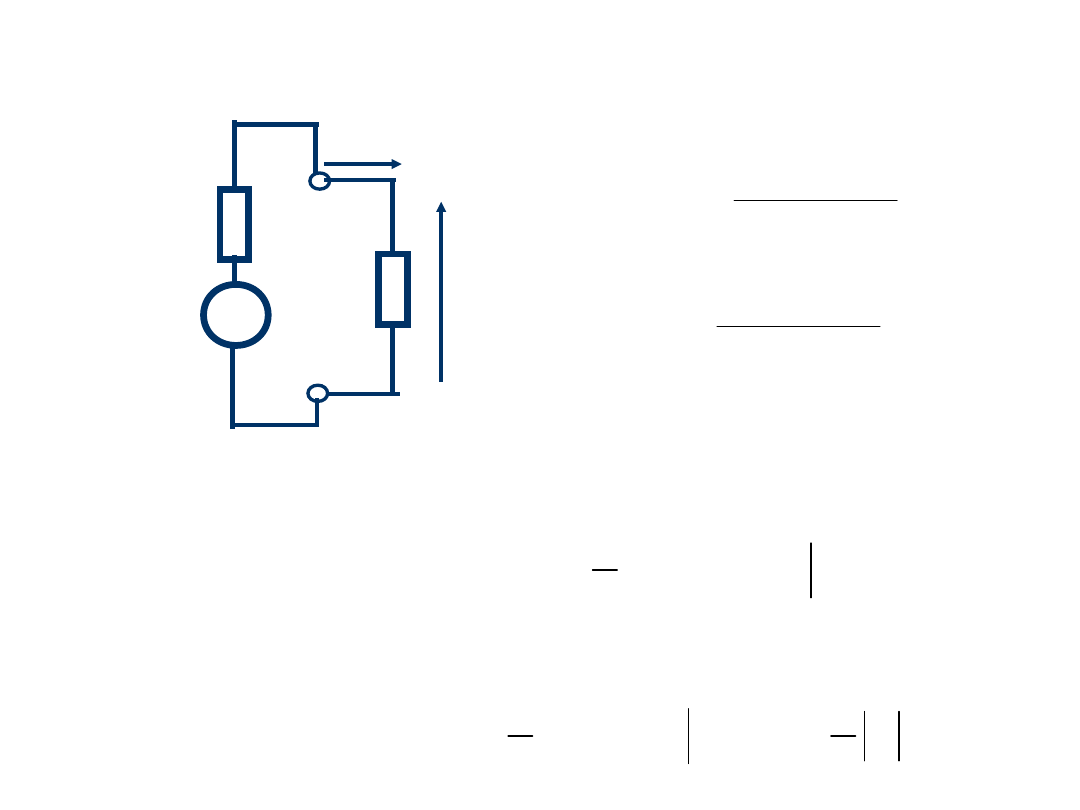
Obwód równoważny linii w punkcie

Obwód równoważny linii w punkcie

zasilania z generatora z = 0

zasilania z generatora z = 0

Średnia moc dostarczona z generatora:

G

we

G

we

G

G

we

we

we

Z

Z

U

I

U

Z

Z

Z

V









Z

G

U

G

Z

w

e

V

we

I

we

l

z

z







'

,

*
we

we

śr

]

I

Re[V

P

0

2

1

Średnia moc dostarczona do obciążenia:

L

L

'

,

*

L

L

śr

R

I

]

I

Re[V

P

2

0

2

1

2

1







 z

l

z

42

42

42

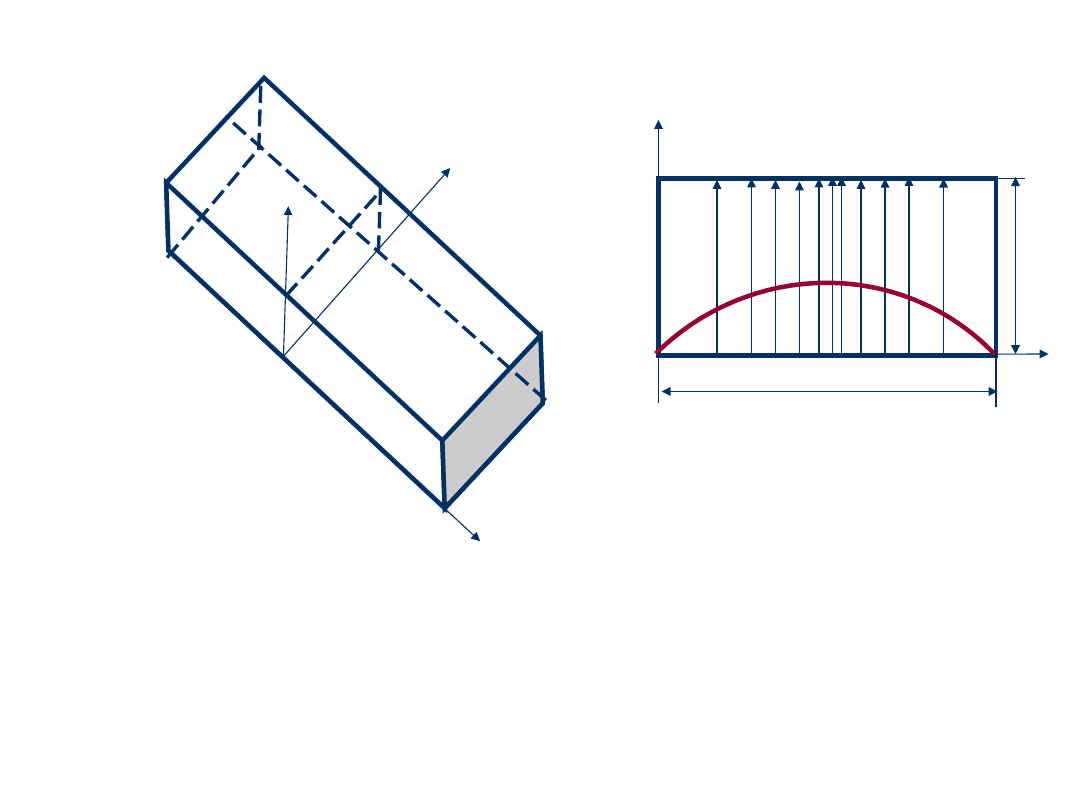
Podstawy teorii falowodów

Podstawy teorii falowodów

Aby pole E

y

spełniło warunki brzegowe musi

zachodzić:

)

(

z

k

t

j

x

0

y

z

x)e

sin(k

E

E







y

z

x

a

b

a

b

E

E

y

i

,

a

x

0

x

0

x)

sin(k

x







zatem:

...

,

,

,

3

2

1

n

n

x

k

x







43

43

43

Ponieważ wewnątrz falowodu nie ma ładunków, to
dywergencja wektora E musi być równa 0:

sprawdzam
y:

0

0

y

E

0

z

E

y

E

x

E

y

z

y

x

































 E

Pole E musi spełniać równanie falowe:

0

t

E

c

1

z

E

y

E

x

E

2

y

2

2

2

y

2

2

y

2

2

y

2

























y

2

2

y

2

y

2
z

2

y

2

2

y

2

y

2
x

2

y

2

E

t

E

E

k

z

E

0

y

E

E

k

x

E

































,

,

,

(*

)

podstawiając do
(*):

0

E

c

E

k

E

k

y

2

2

y

2
z

y

2
x







-

(**

)

44

44

44

Zakładamy oczywiście, że E  0 dla x  [0,a], zatem

Fala E przemieszcza się w falowodzie w kierunku osi
z tylko wtedy, gdy liczba falowa spełnia warunek (x).
Z tego warunku wynika wzór na dolną częstotliwość
graniczną fali, jaka może być przenoszona przez
falowód:

Ale k

x

jest już ustalone wcześniej k

x

=  / a , zatem:

0

c

k

k

2

2

2
z

2

x







-

2

2

z

a

c

k











 













 





(x

)

a

2

c

f

a

c

f

2

g

g

g











