LINIE NORMATYWNE
JAKO OCENA WYKONYWANIA
CZYNNOŚCI OBARCZONYCH O
STAŁYM WSPÓŁCZYNNIKU
ZMIENNOŚCI
Normatywy czasowe wykonania
czynności,
oprócz
uwzględniania
czynników wpływających przypadkowo
na czas ich realizacji, mogą także
uwzględniać czynniki systematyczne.
Należą do nich: obniżanie wydajności
pracownika wraz z upływem czasu,
zwiększenie pracochłonności wraz z
pogarsza-jącymi się warunkami pracy
(np. praca na coraz to większej
wysokości murarki).
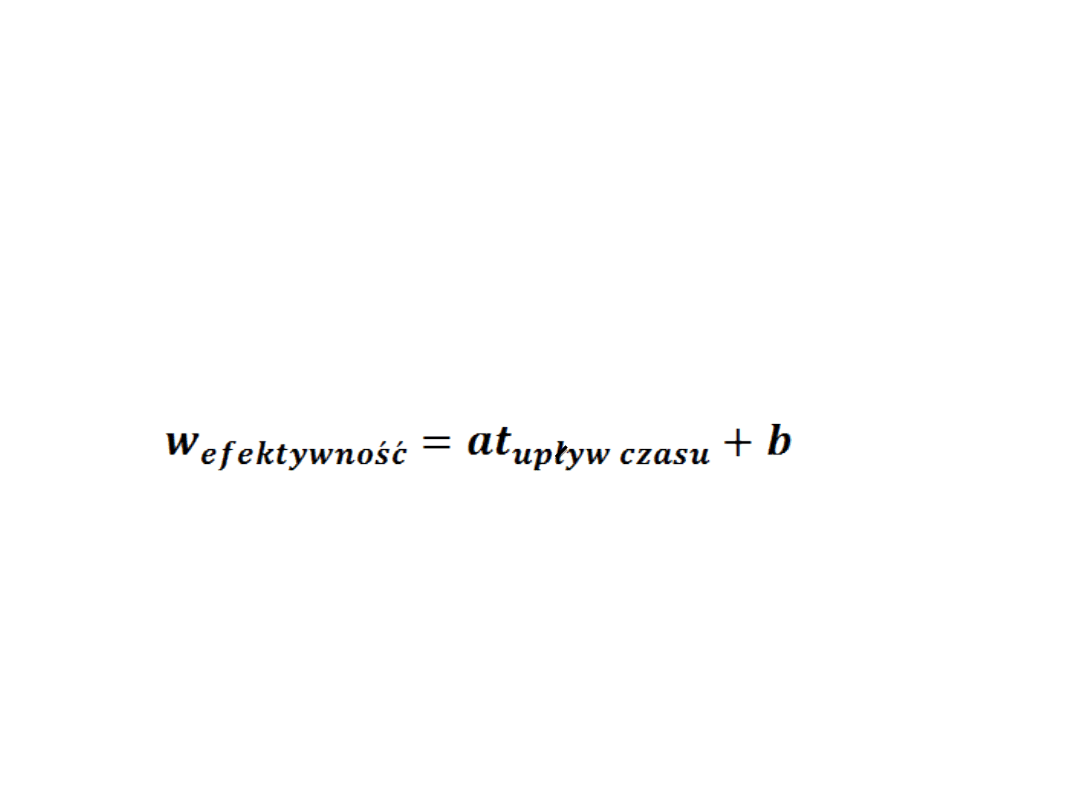
Najczęściej ocenę zmiany normy z
powodów
działania
czynnika
o
charakterze
systematycznym
przedstawia się za pomocą funkcji
określającej
zmieniający
się
czas
wykonania roboty w zależności od
poziomu czynnika ją utrudniającego.
Najprostszą funkcją opisującą taki
czynnik jest prosta regresji. Prosta ta o
równanie
(1)
w którym współczynnika a i b prostej
zależą
od
rodzaju
wykonywanej
czynności.
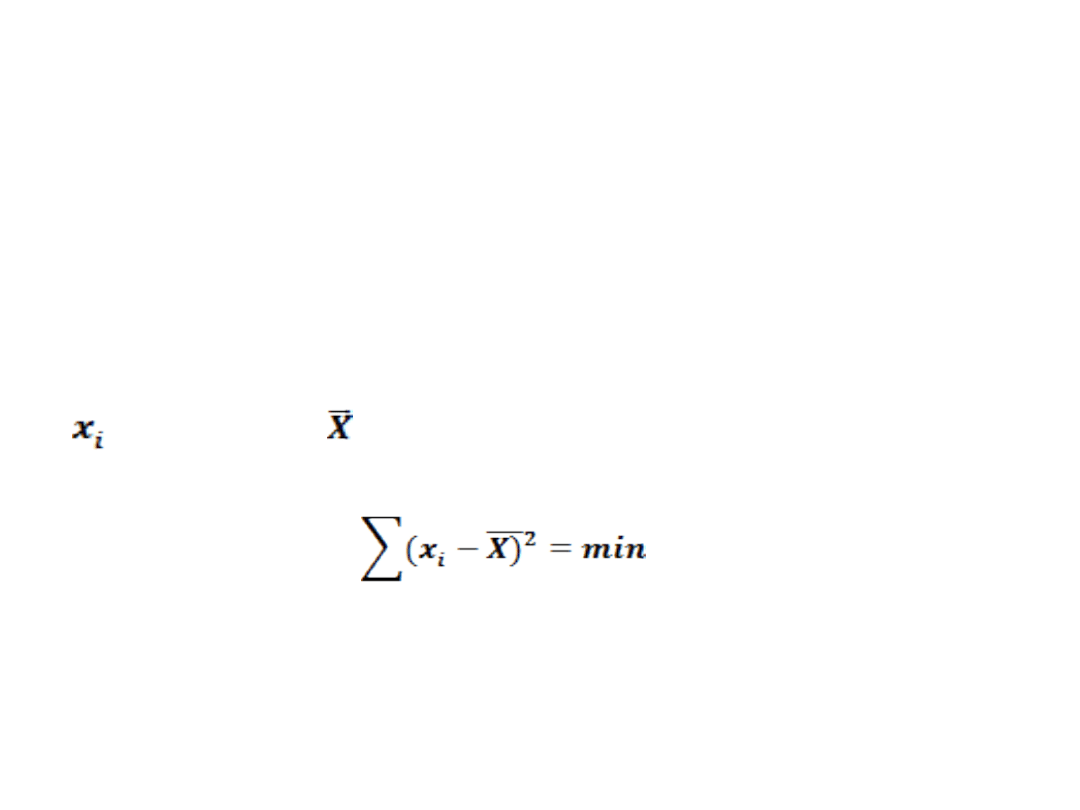
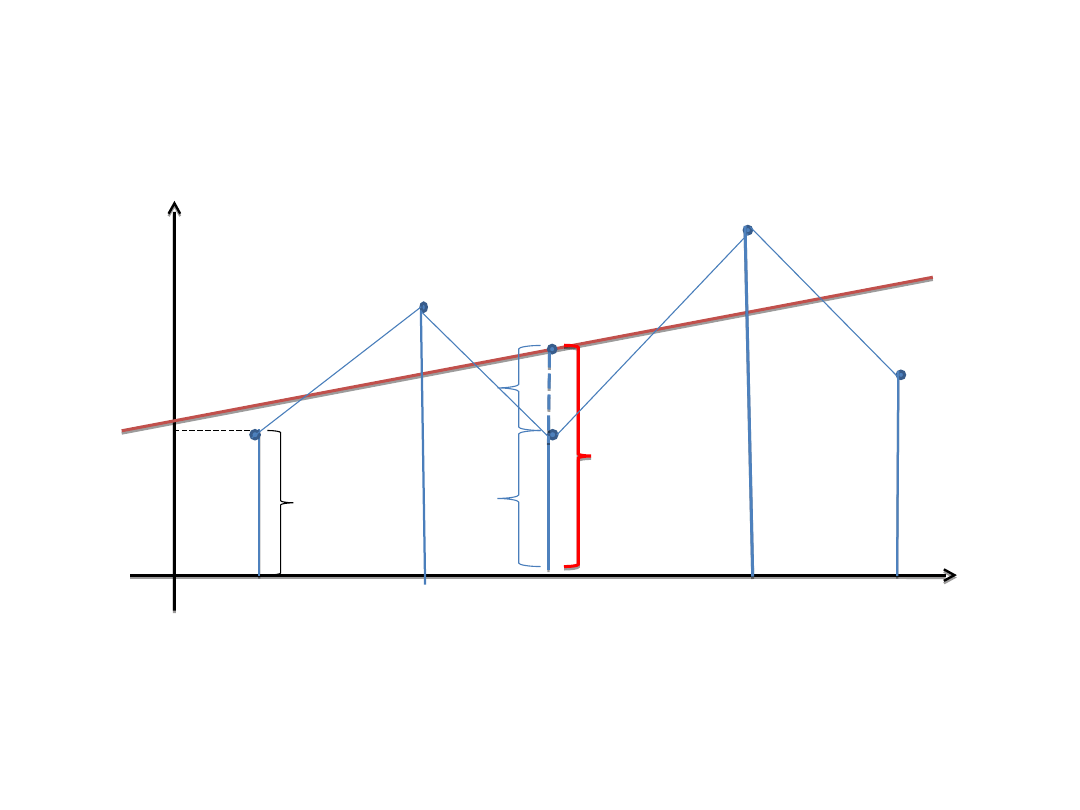
Pozyskanie więcej danych aniżeli jest
to potrzebne do wyznaczenia równania tej
prostej prowadzi do poszukiwania takiego
rozwiązania, które „najlepiej” wpiszą się w
te dane. Na bazie statystyki stwierdzono,
że musi ono spełniać kryterium minimum
sumy
kwadratów
odchyleń
od
wyznaczających je danych.
Przyjmując, że odchylenie poszczególnej
danej pomiarowej
od wartości reprezentującej
rozwiązanie zadania,
kryterium to zapisujemy równaniem:
(2)
a jego realizację nazywamy rozwiązaniem
„metodą najmniejszych kwadratów”.
W
X
w
i
po
m
x
i
v
i
w
i
wyr
prost
a
regre
sj
i
Teoria wyznaczenia
równania regresji
w
i
po
m
i =
1
i =
n
w
wyr
=ax
+b
Rozwiązanie zadania polega na
wyznaczeniu współczynników a oraz b
równania o postaci
w
i
wyr
= ax
i
+ b
(3)
Czynność
tę
nazywany
też
aproksymacją
zbioru
danych
za
pomocą funkcji liniowej.
APROKSYMACJA: 1. książkowo: ujęcie czegoś w sposób
niezupełnie ścisły; przybliżenie; 2. w matematyce:
zastąpienie wielkości matematycznych innymi, o
przybliżonych własnościach, łatwiejszymi do badania i
zastosowania.
Zastępując w równaniu (3)
poszukiwane
wielkości
w
i
wyr
niezbędnymi
do
ich
wyznaczenia
wynikami
pomiarów
w
i
pom
(które
obarczone są błędami przypadkowymi)
oraz odchyłkami od poszukiwanej
prostej v
i
(zmienią te obserwacje na
najbardziej
prawdopodobne)
zapiszemy
w
i
wyr
= w
i
pom
+ v
i
(2)
skąd
v
i
= w
i
wyr
– w
pom
= ax + b – w
pom
(3)
co dla n pomiarów daje układ równań
v
1
= ax
1
+ b – w
1
pom
v
2
= ax
2
+ b – w
2
pom
--------------------------
(4)
v
n
= ax
n
+ b – w
n
pom
co zapisane w postaci macierzowej
przyjmuje postać
V = A∙dU + W
(5)
gdzie :
V – macierz odchyłek
zaobserwowanych wielkości
od wartości
najprawdopodobniejszej,
A – macierz współczynników przy
niewiadomych,
dU – macierz poszukiwanych
niewiadomych
W = (W
i
przybl
– W
i
pom
) – macierz
wyrazów wolnych.
Układ tych równań zawiera (n+2)
niewiadome. Są to n niewiadomych v
i
oraz niewiadome a i b. Ich rozwiązane
jest możliwe dzięki wprowadzeniu
warunku [v
2
]=min.
Rozwiązaniem tego układu metodą
najmniejszych kwadratów jest wektor
niewiadomych dU
dU = (A
T
∙ A)
-1
∙ A
T
∙ W
(6)
Na podstawie poprawek dU liczony
jest
wektor
V
poprawek
do
pomierzonych wielkości
W
pom
:
V = A∙dU + W = A ∙ (A
T
∙A)
-1
∙ A
T
∙
W + W
(7)
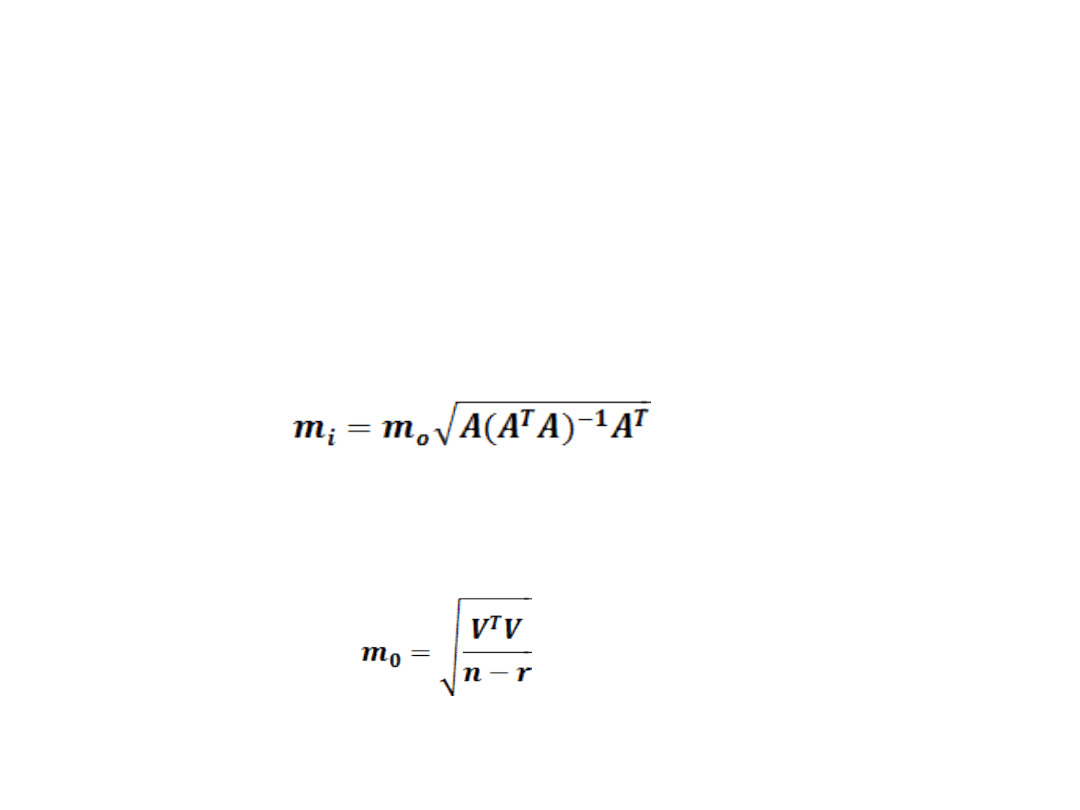
OCENA DOKŁADNOŚCI
Pomierzenie większej liczby
obserwacji aniżeli jest to niezbędne
do jednoznacznego wyznaczenia
zadania pozwala na określenie
dokładności wyznaczonych
parametrów. Błędy średnie
wyrównanych wielkości oblicza się z
zależności:
(10)
gdzie m
o
oznacza błąd typowego
spostrzeżenia określonego dla n
równań o r niewiadomych wzorem
ZADANIA NA ĆWICZENIA
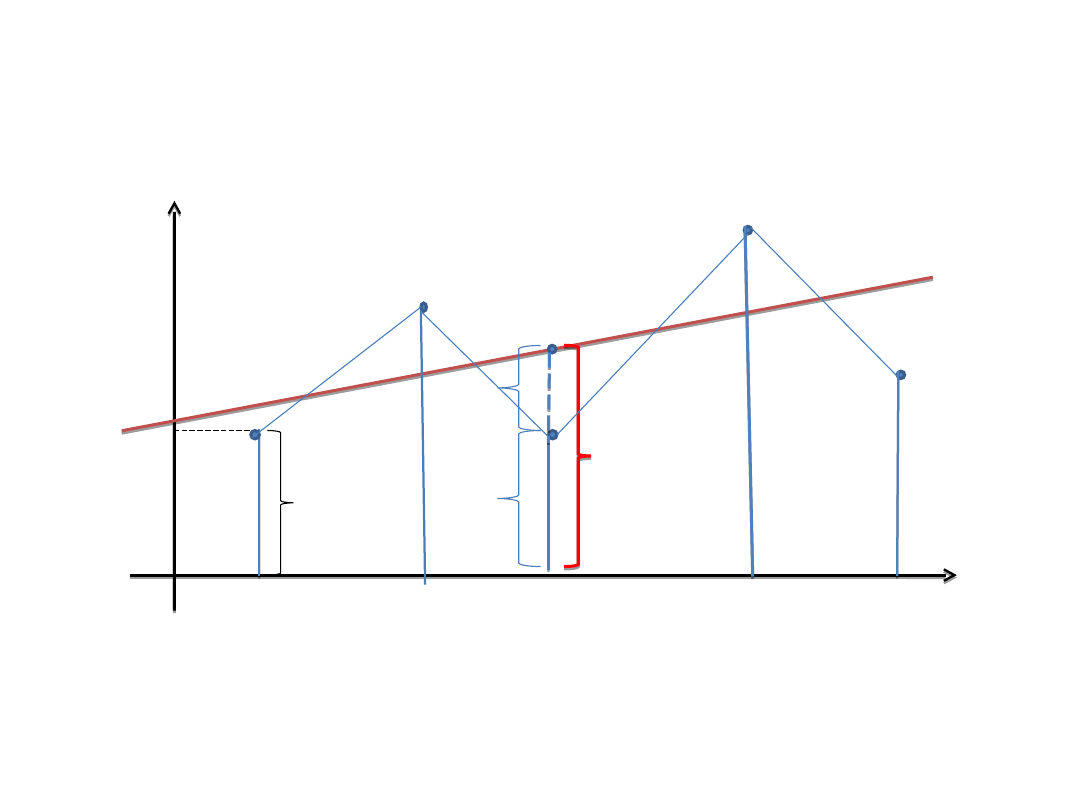
W
X
w
i
po
m
x
i
v
i
w
i
wyr
prost
a
regre
sj
i
Zadanie na wyznaczenie równania
regresji
w
i
po
m
i =
1
i =
n
w
wyr
=ax
+b
Na podstawie danych w tabeli wyznaczyć
równanie regresji dla (7+n) obserwacji
prostoliniowego
odcinka,
gdzie
n
jest
indywidualną liczbą dla studenta.
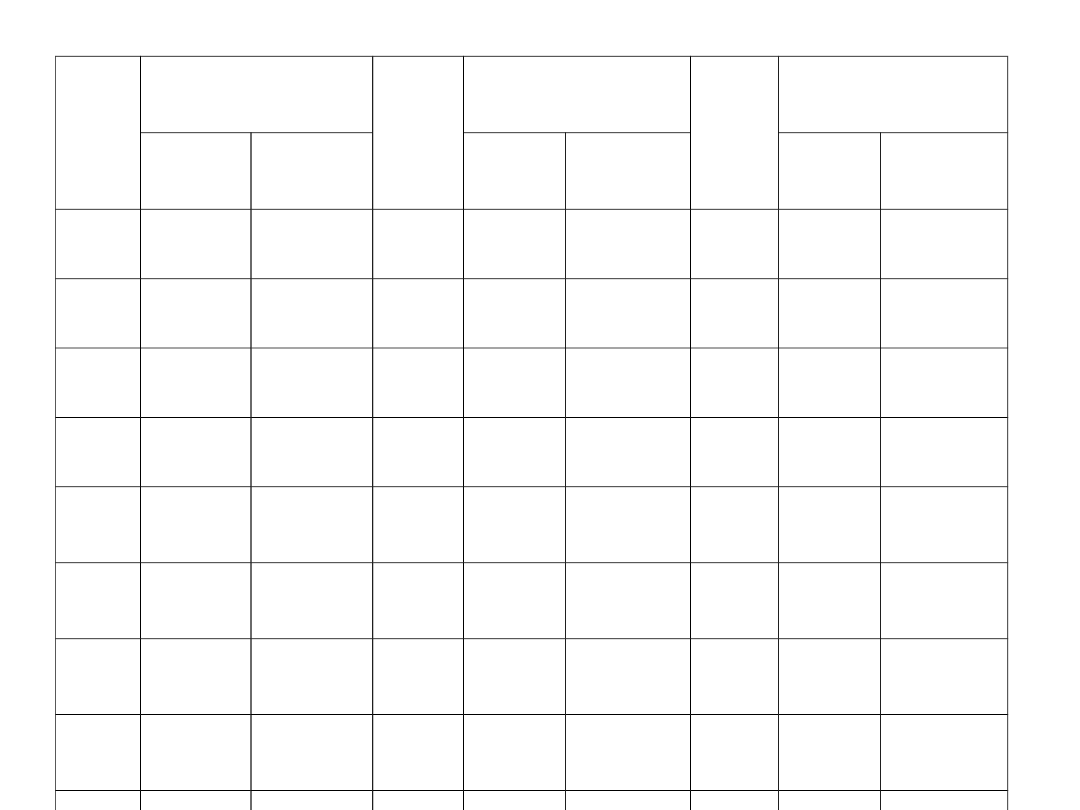
Nr
punk
tu
Odległości po
prostej
[mm]
Nr
punkt
u
Odległości po
prostej
[mm]
Nr
punk
tu
Odległości po
prostej
[m]
wzdłuż
L
w
poprzek
W
wzdłu
ż
L
w
poprzek
W
wzdłu
ż
L
w
poprzek
W
1
2000
17
14
2800
0
31
27
5400
0
62
2
4000
30
15
30,0
00
37
28
5600
0
65
3
6000
28
16
3200
0
47
29
5800
0
71
4
8000
22
17
3400
0
36
30
6000
0
63
5
1000
0
32
18
3600
0
37
31
6200
0
70
6
1200
0
25
19
3800
0
47
32
6400
0
68
7
1400
0
16
20
4000
0
46
33
6600
0
75
8
1600
0
35
21
4200
0
51
34
6800
0
70
9
1800
0
23
22
4400
0
48
35
7000
0
71
10
2000
0
25
23
4600
0
56
36
7200
0
79
11
2200
0
39
24
4800
0
62
37
7400
0
80
12
2400
0
32
25
5000
0
57
38
7600
0
75
13
2600
0
25
26
5200
0
70
39
7800
0
80
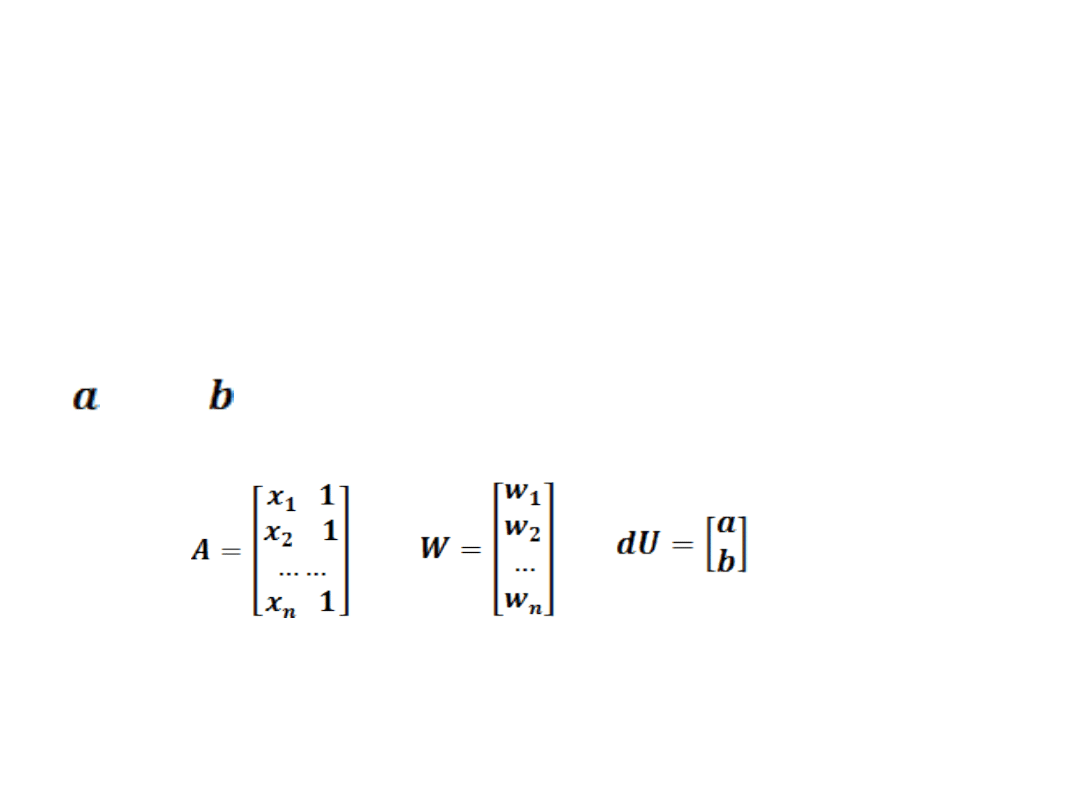
PRZYKŁAD
W omawianym zadaniu, na podstawie
układu równań
v
1
= ax
1
+ b – w
1
pom
v
2
= ax
2
+ b – w
2
pom
--------------------------
(4)
v
n
= ax
n
+ b – w
n
pom
wyznaczane są współczynniki równania
prostej regresji
oraz . Zapisane w postaci
macierzowej
V = A∙dU + W tworzą tablice:
Zgodnie z zadaniem, dla pierwszych siedmiu
danych otrzymujemy
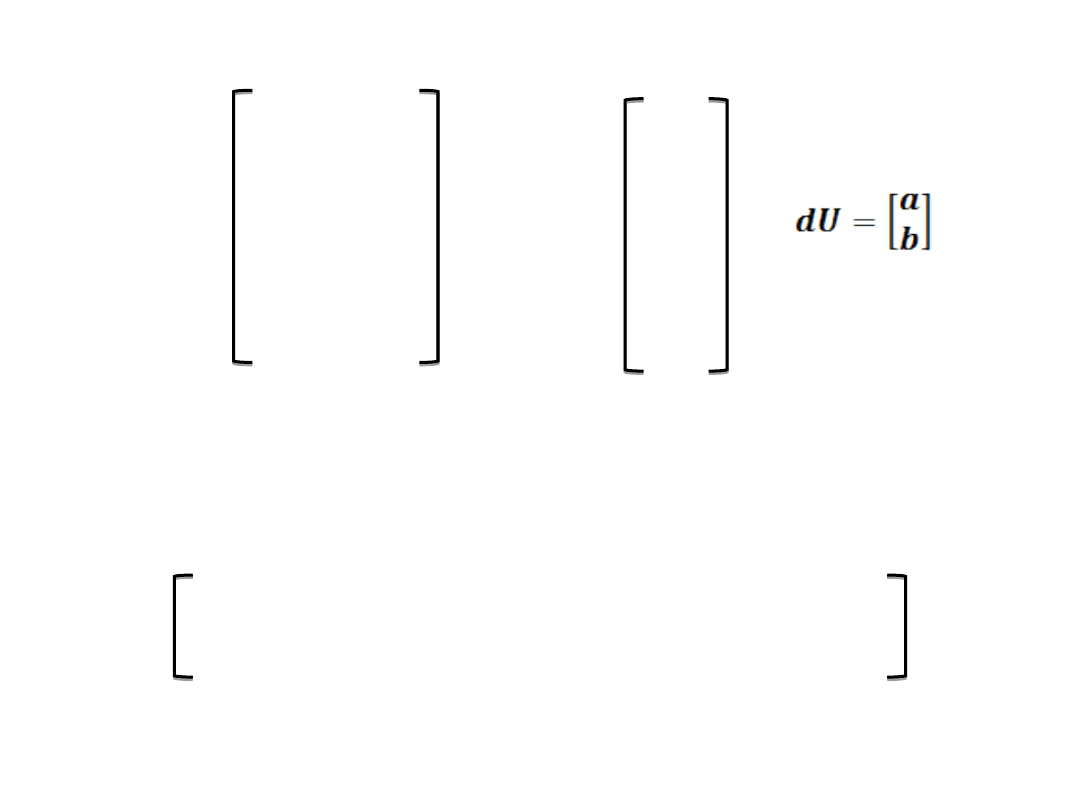
2000
1
4000
1
6000
1
A =
8000
1
1000
0
1
1200
0
1
1600
0
1
11
30
28
W =
22
32
25
16
W celu znalezienia rozwiązania dU =
(A
T
∙ A)
-1
∙ A
T
∙ W liczymy kolejno:
1) transpozę macierzy: A
T
;
(=transponuje)
2000 4000 6000 8000 10000 12000 16000
1
1
1
1
1
1
1
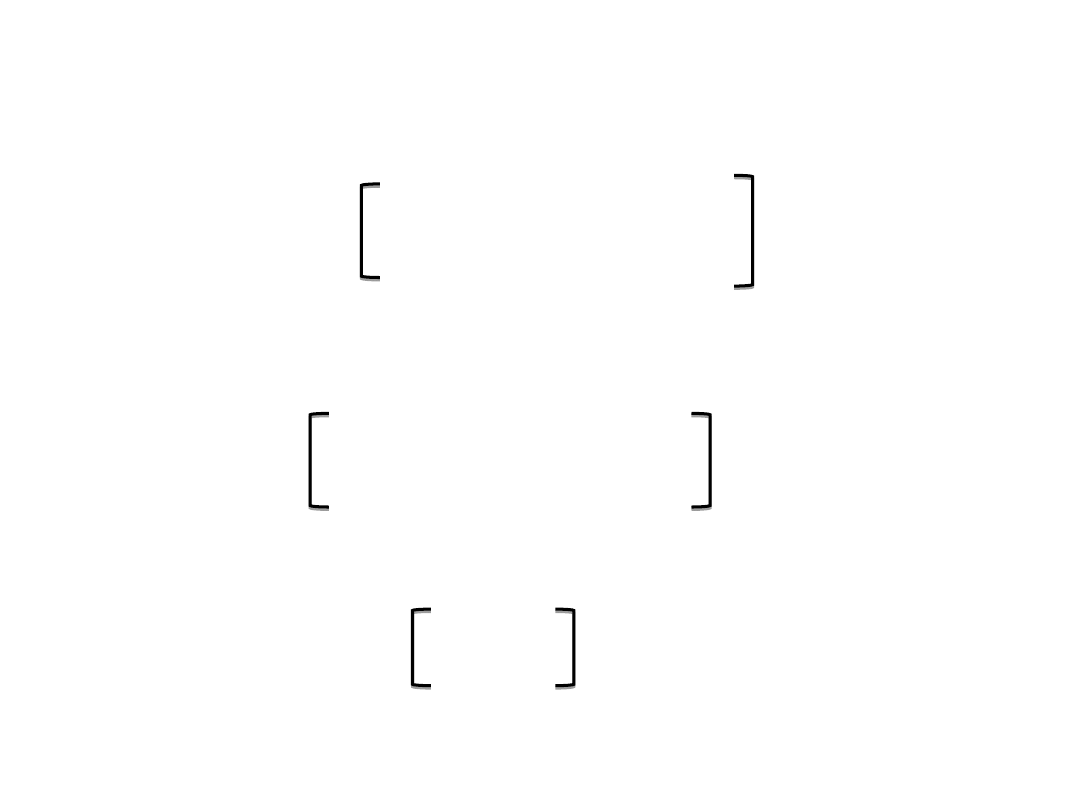
2) iloczyn macierzy: A
T
∙A ;
(=macierz.iloczyn)
3) odwrotność iloczynu w/w
macierzy: (A
T
∙A )
-1
(=macierz.odw)
(A
T
∙A)
-1
= 7,1721E-09 -5,9426E-05
-5,943E-05 0,6352459
4) iloczyn macierzy: A
T
∙W ;
(=macierz.iloczyn)
A
T
∙W = 1362000
164
A
T
∙A
=
62000000
0
58000
58000
7
5) iloczyn macierzy wyznaczający
szukane współczynniki równania:
dU = (A
T
∙ A)
-1
∙ (A
T
∙ W) ;
(=macierz.iloczyn)
POSZUKIWANE RÓWNANIE
PROSTEJ:
w = 0,0000254x +
23,24
dU =
2,2541E-05
23,2418032
8
KONIEC ZADANIA
NA WYZNACZENIE WSPÓŁCZYNNIKÓW RÓWNANIA
REGRESJI
Obliczenie poprawek regulacyjnych
do prostej zgodnie z zależnością V =-
A∙dU+W.
6) obliczamy iloczyn macierzy: A
T
∙dU
(=macierz.iloczyn)
i odejmujemy od
wyniku macierz W gdyż poprawki mają
znak przeciwny do odchyłki
(=macierz1 -
macierz2)
.
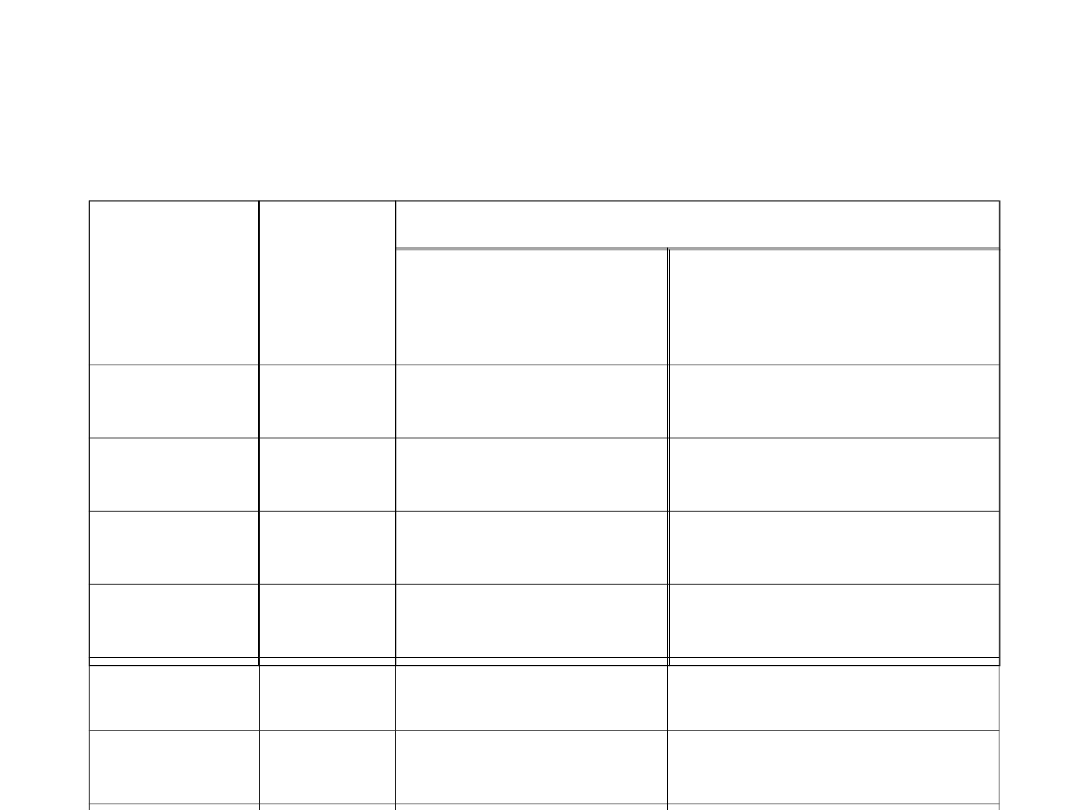
A ∙ dU - W = V = V
23,29 11 + 12,29 +12,3
23,33 30 - 6,67 - 6,7
23,38 28 - 4,62 - 4,6
23,42 22 + 1,42 +1,4
23,47 32 - 8,53 - 8,5
23,51 25 - 1,49 - 1,5
23,60 16 + 7,60 +
7,6
KONTROLA WYNIKÓW polega na
dwukrotnym obliczeniu współrzędnych
punktów na wyznaczonej prostej
Nr
punktu
x
i
Według zależności
w
wyr
= w
i
+ v
i
w
wyr
= ax
i
+ b
w = 0,0000254x +
23,24
1
2000
11 + 12,29 =
23,29
23,29
2
4000
30 – 6,67 =
23,33
23,34
3
6000
28 – 4,62 =
23,38
23,39
4
8000
22 + 1,42 =
23,42
23,44
5
10000
32 – 8,53 =
23,57
23,49
6
12000
25 – 1,49 -=
23,51
23,54
7
14000
16 + 7,60 =
23,60
23,60
PRZYDATNE RADY
MNOŻENIE DWÓCH MACIERZY JEST
WYKONALNE GDY DRUGA MACIERZ MA TYLE
WIERSZY ILE PIERWSZA MA KOLUMN ; ICH
ILOCZYN MA TYLE WIERSZY ILE PIERWSZA MA
WIERSZY I TYLE KOLUMN ILE DRUGA MA
KOLUMN
TRANSPOZA MACIERZY A POWSTAJE PRZEZ
ZAMIANĘ KOLEJNYCH JEJ WIERSZY NA KOLEJNE
KOLUMNY MACIERZY, natomiast
ODWROTNOŚĆ MACIERZY A
T
MA TAKIE
WYMIARY JAK JEJ TRANSPOZA
MNOŻENIE MACIERZY PRZEZ LICZBĘ TO
MNOŻENIE JEJ PRZEZ MACIERZ DIAGONALNA.
MA ONA STALE NA PRZEKĄTNEJ MNOŻNIK A
POZOSTAŁE POZYCJE MAJĄ ZERA
DODAWANIE
MACIERZY
(wpisujemy
do
beleczki znak „równa się” poczym klikamy
na pierwszy wyraz macierzy 1 i przeciągamy
to na całość tablicy, następnie wpisujemy
znak dodawania (tu minus bo wyliczyliśmy
odchyłki a poszukujemy poprawek, które
mają znak przeciwny) i klikamy na pierwszy
wyraz drugiej macierzy i znowu przeciągamy
to
na
całą
drugą
tablicę.
Po
tych
czynnościach akceptujemy działanie jak dla
macierzy, tj. wciskając ctr+shift+enter.
Uwaga: macierze muszą mieć taki sam
wymiar.
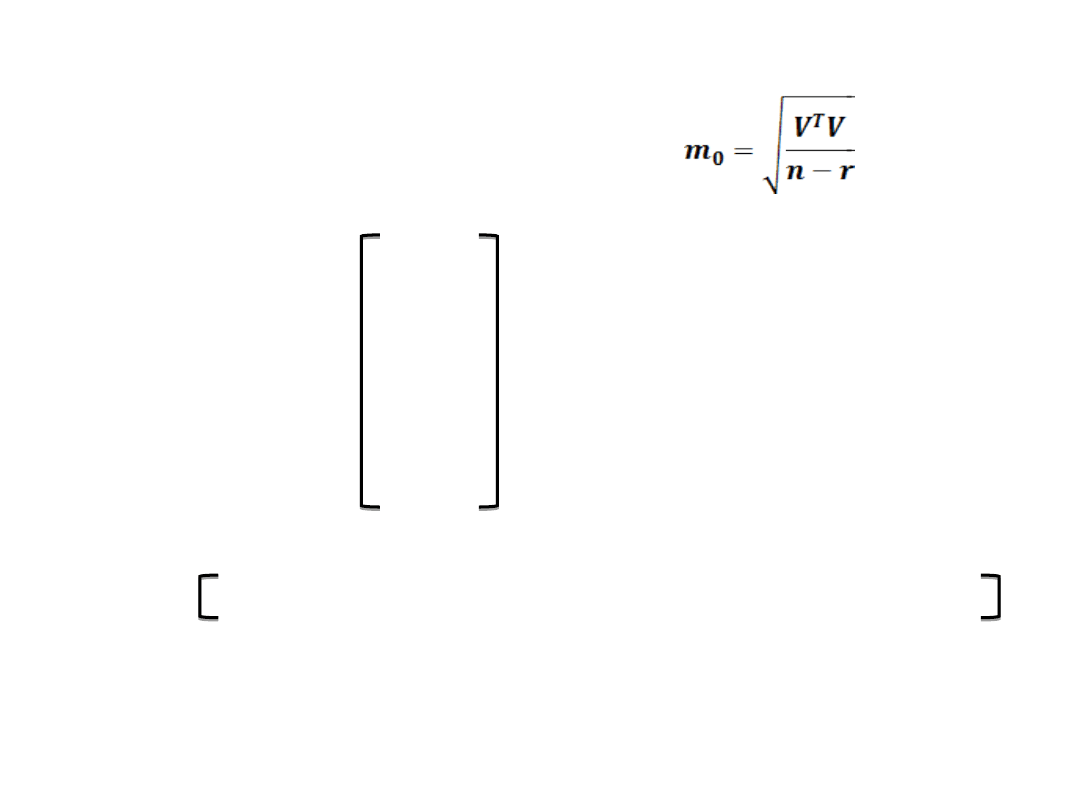
OCENA DOKŁADNOŚCI
7) OBLICZENIE WARIANCJI σ
2
dla wzoru
n – r
= 5
n – liczba
pomiarów
r – liczba
poszukiwanych
niewiadomych (a, b)
;
m
0
= ± 8,38
12,287
-6,668
-4,623
V
=
1,422
-8,533
-1,488
7,602
V
T
=
12,28
7 -6,668
-
4,623 1,422
-
8,533 -1,488 7,602
V
T
V
=
351,6434
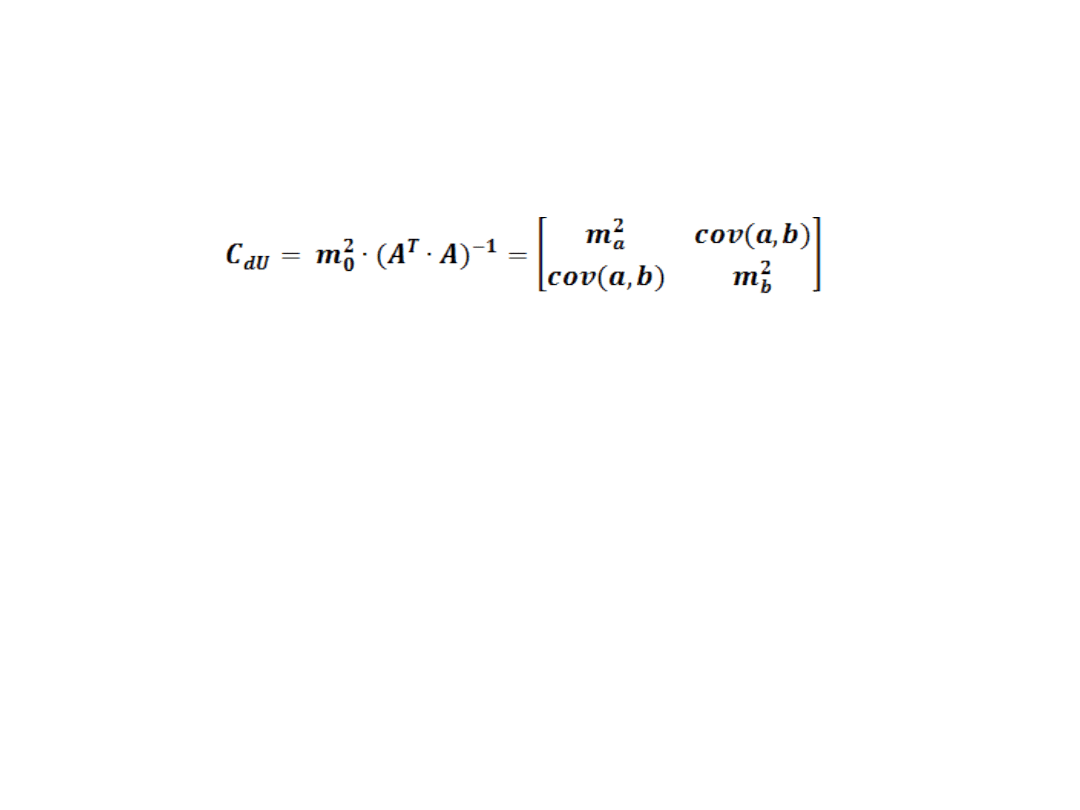
OBLICZENIE BŁĘDÓW ŚREDNICH
OBLICZONYCH PARAMETRÓW RÓWNANIA
REGRESJI
Nr
W
przybl
błą
d
L
[m
]
W
obs
1
5,470
0
2
2
5,740
+18
4
3
6,010
-12
6
4
6,280
-8
8
5
6,550
+5
10
6
6,820
+32 12
7
7,090
+23 14
8
7,360
0
16
9
7,630
-26
18
10
7,900
-16
20
DLA MNIE
Tablica danych wyjściowych y =
n∙2,000∙0,1350 + 5,200
Nr
zad
ani
a
W
przybl
błąd
L
[m
]
W
obs
11
0
22
12
+28
24
13
-12
26
14
-18
28
15
+5
30
16
+22
32
17
+23
34
18
0
36
19
-36
38
20
-26
40
DLA MNIE
Tablica danych wyjściowych y =
n∙2,000∙0,1350 + 5,200
Nr
W
przybl
błąd
L
[m]
W
obs
21
+30
42
22
+18
44
23
-2
46
24
-8
48
25
+15
50
26
+2
52
27
-23
54
28
0
56
29
-26
58
30
+16
60
DLA MNIE
Tablica danych wyjściowych y =
n∙2,000∙0,1350 + 5,200