BADANIA

BADANIA

OPERACYJN

OPERACYJN

E

E

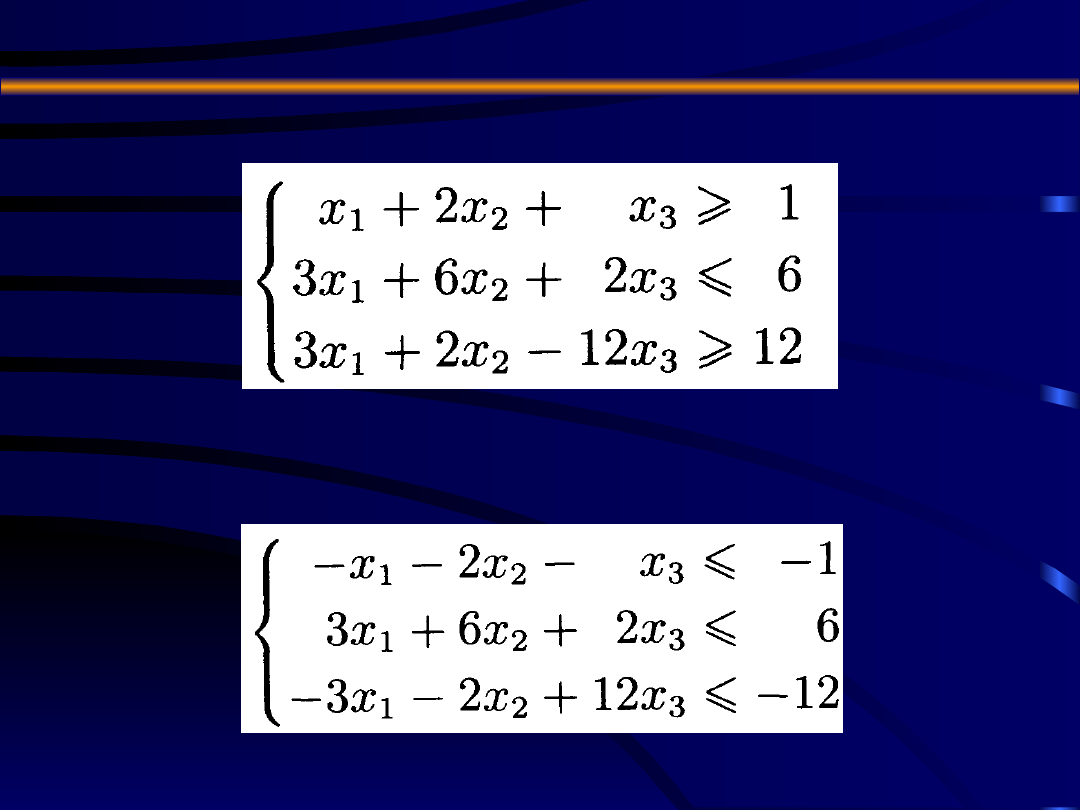
PRZYKŁAD 1:

PRZYKŁAD 1:

Rozpatrzmy następujący układ nierówności

Rozpatrzmy następujący układ nierówności

liniowych

liniowych

W celu rozwiązania tego układu

W celu rozwiązania tego układu

zapisujemy go najpierw w postaci

zapisujemy go najpierw w postaci

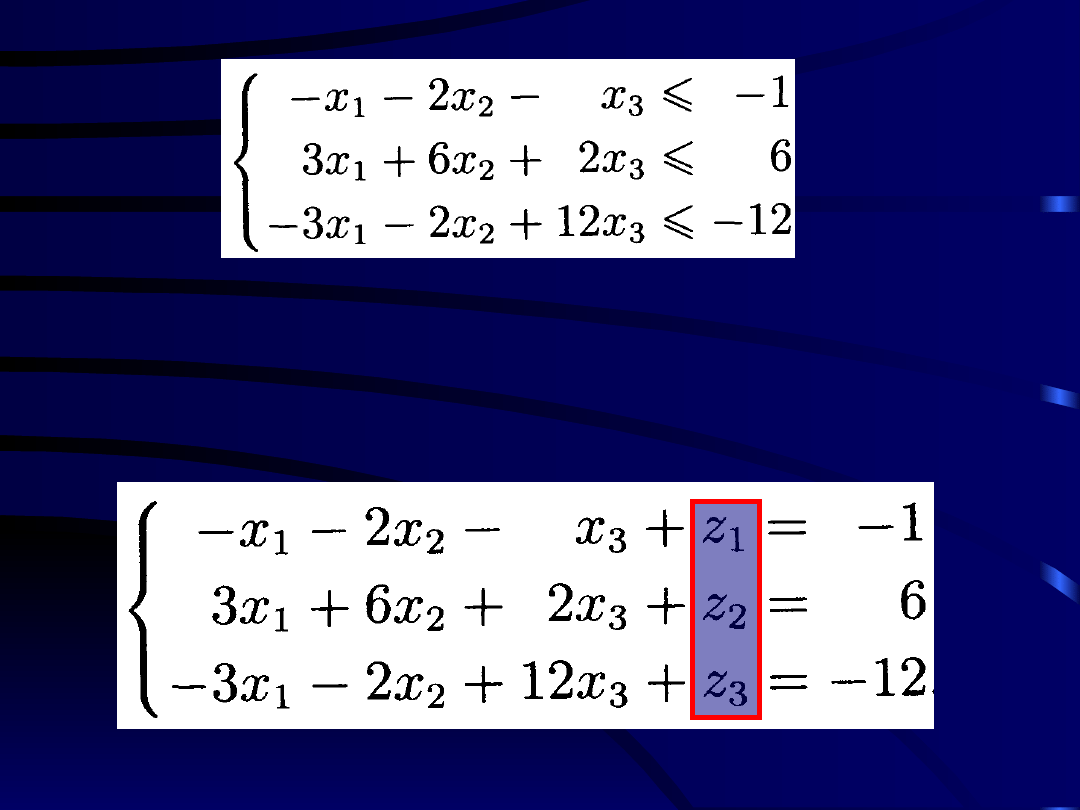
W celu rozwiązania tego układu zapisujemy go

W celu rozwiązania tego układu zapisujemy go

najpierw w postaci

najpierw w postaci

Następnie tworzymy układ równań

Następnie tworzymy układ równań

liniowych odpowiadający powyższemu

liniowych odpowiadający powyższemu

układowi nierówności liniowych. Ma on

układowi nierówności liniowych. Ma on

postać

postać

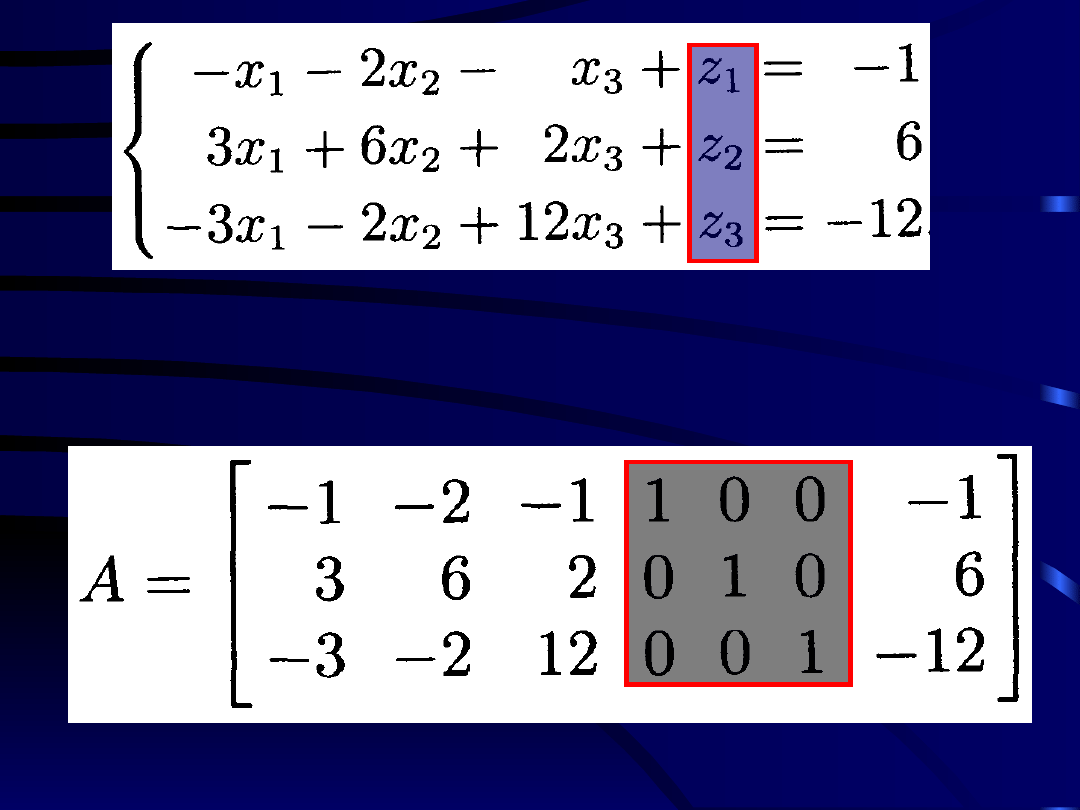
Rozważamy dalej macierz uzupełnioną

Rozważamy dalej macierz uzupełnioną

powyższego układu równań liniowych:

powyższego układu równań liniowych:

Następnie wykonujemy operacje

Następnie wykonujemy operacje

elementarne na macierzy A, dzięki

elementarne na macierzy A, dzięki

którym po lewej stronie tej macierzy

którym po lewej stronie tej macierzy

pojawia się macierz jednostkowa.

pojawia się macierz jednostkowa.

W tym celu mnożymy pierwszy wiersz

W tym celu mnożymy pierwszy wiersz

macierzy A przez liczbę 3 i dodajemy

macierzy A przez liczbę 3 i dodajemy

do drugiego wiersza,

do drugiego wiersza,

a następnie mnożymy pierwszy wiersz

a następnie mnożymy pierwszy wiersz

przez liczbę

przez liczbę

-3 i dodajemy do trzeciego wiersza.

-3 i dodajemy do trzeciego wiersza.

Otrzymujemy

Otrzymujemy

Przestawiamy teraz drugi wiersz z

Przestawiamy teraz drugi wiersz z

trzecim i mamy

trzecim i mamy

Następnie mnożymy pierwszy wiersz

Następnie mnożymy pierwszy wiersz

przez -1, drugi przez 1/4, a trzeci przez

przez -1, drugi przez 1/4, a trzeci przez

-1 i uzyskujemy

-1 i uzyskujemy

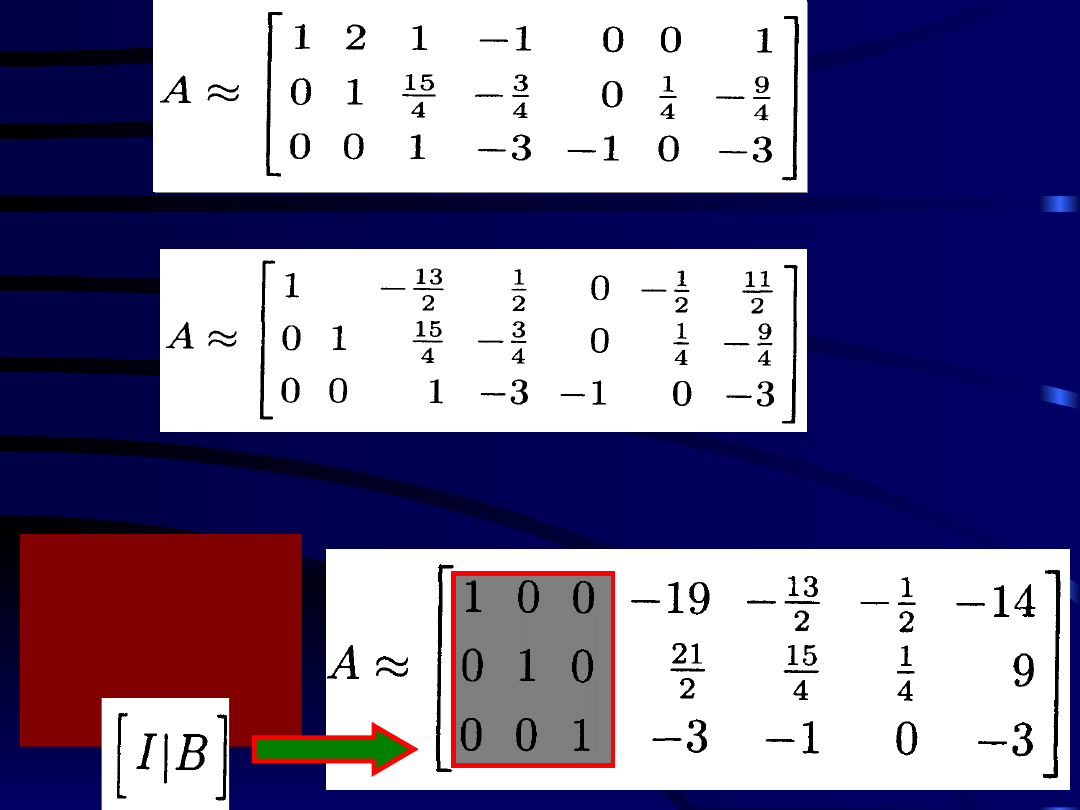
Mnożymy drugi wiersz przez –2 i dodajemy

Mnożymy drugi wiersz przez –2 i dodajemy

do pierwszego

do pierwszego

Mnożymy trzeci wiersz przez –15/4 i

Mnożymy trzeci wiersz przez –15/4 i

dodajemy do drugiego Mnożymy trzeci

dodajemy do drugiego Mnożymy trzeci

wiersz przez 13/2 i dodajemy do pierwszego

wiersz przez 13/2 i dodajemy do pierwszego

Otrzymuje

Otrzymuje

my postać

my postać

bazową

bazową

macierzy

macierzy

0

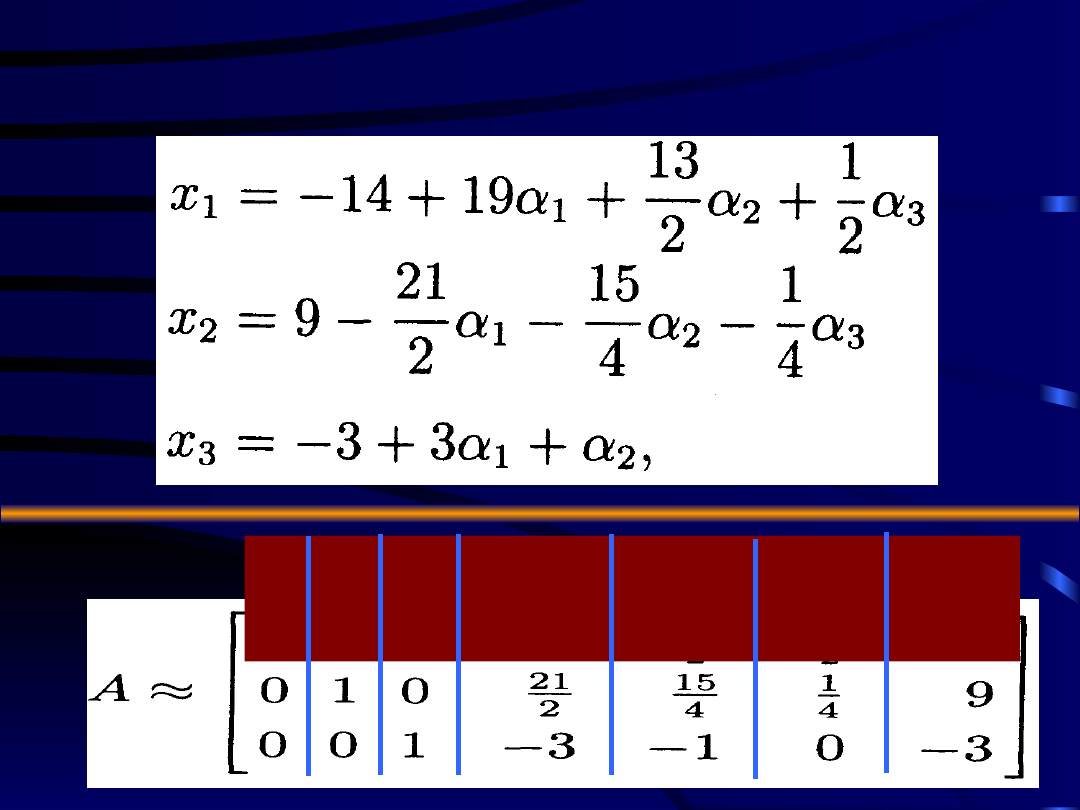
Zgodnie z tw. 1. dany układ

Zgodnie z tw. 1. dany układ

nierówności liniowych ma rozwiązanie,

nierówności liniowych ma rozwiązanie,

które zapisujemy w postaci:

które zapisujemy w postaci:

x

x

1

1

x

x

2

2

x

x

3

3

z

z

1

1

=

=





1

1

z

z

2

2

=

=





2

2

z

z

3

3

=

=





3

3

b

b

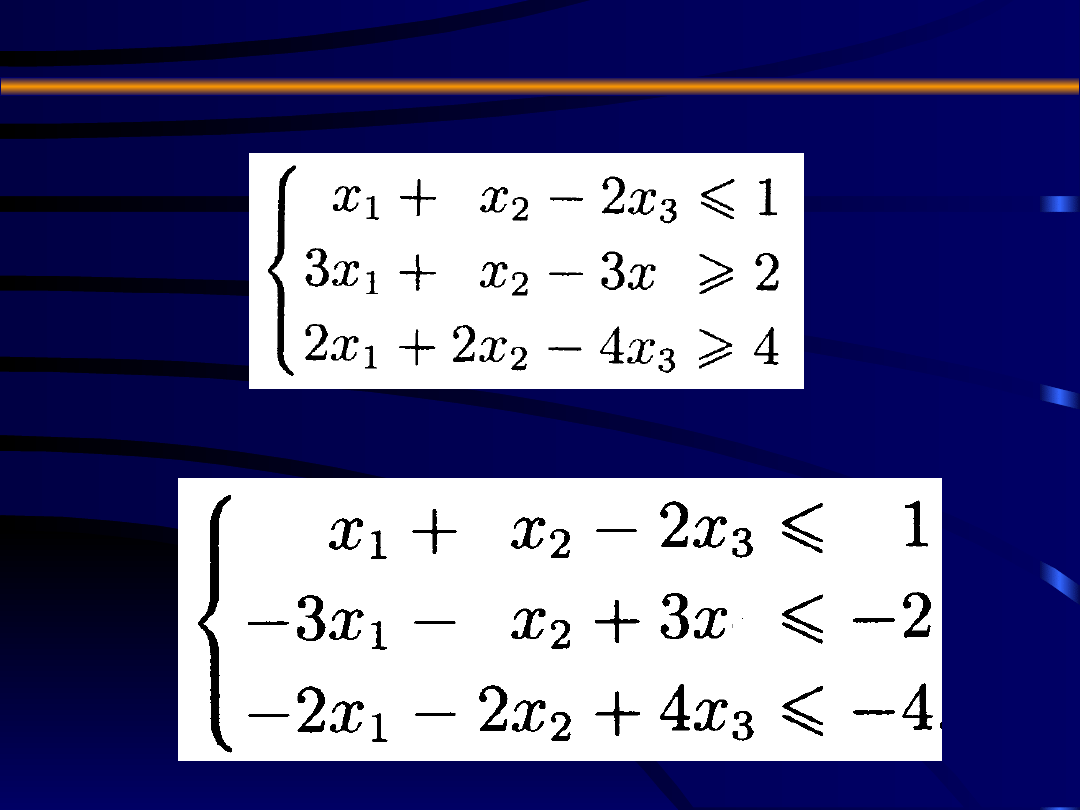
PRZYKŁAD 2:

PRZYKŁAD 2:

Rozpatrzmy następujący układ nierówności

Rozpatrzmy następujący układ nierówności

liniowych

liniowych

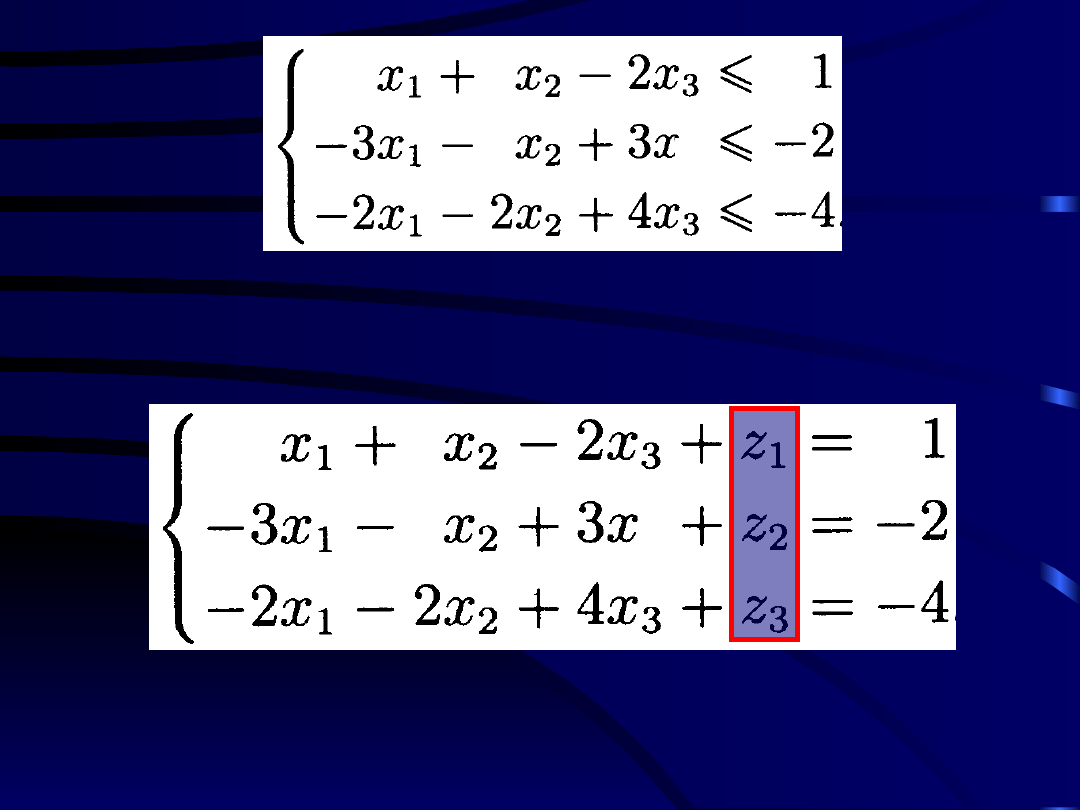
Układ ten zapisujemy w postaci

Układ ten zapisujemy w postaci

3

3

3

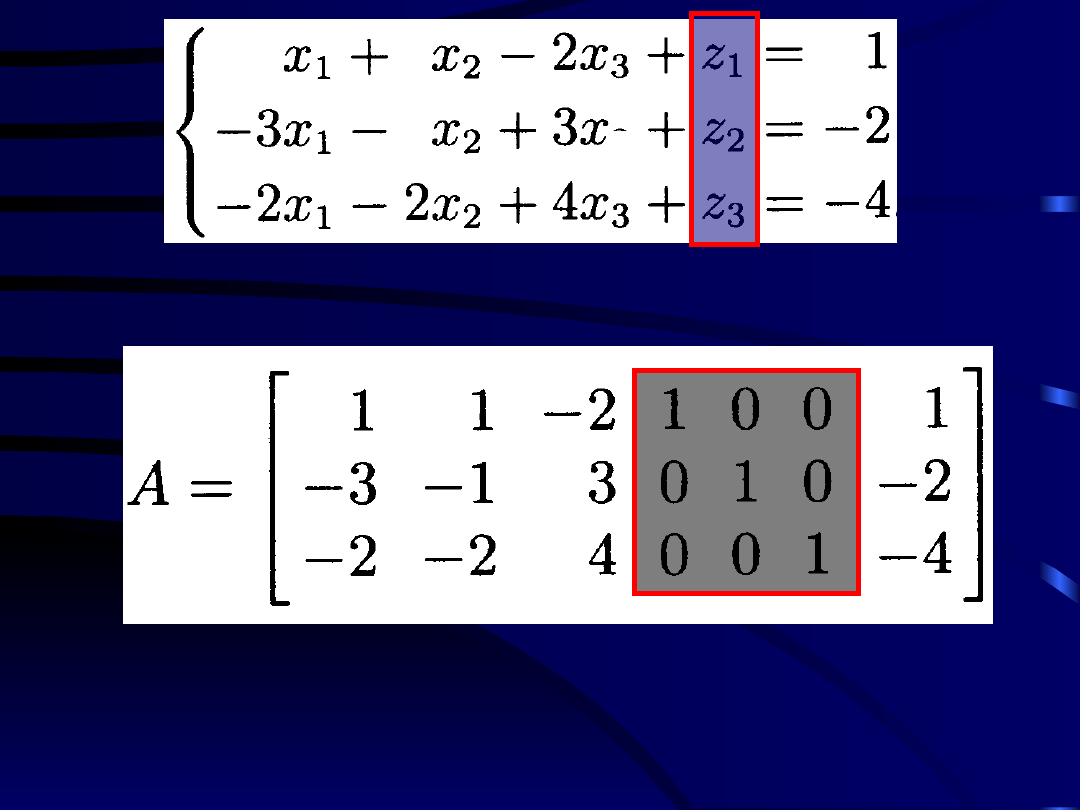
Następnie, powyższy układ nierówności

Następnie, powyższy układ nierówności

zastępujemy odpowiadającym mu układem

zastępujemy odpowiadającym mu układem

równań, który ma postać

równań, który ma postać

3

3

Macierzą uzupełnioną tego układu równań

Macierzą uzupełnioną tego układu równań

jest

jest

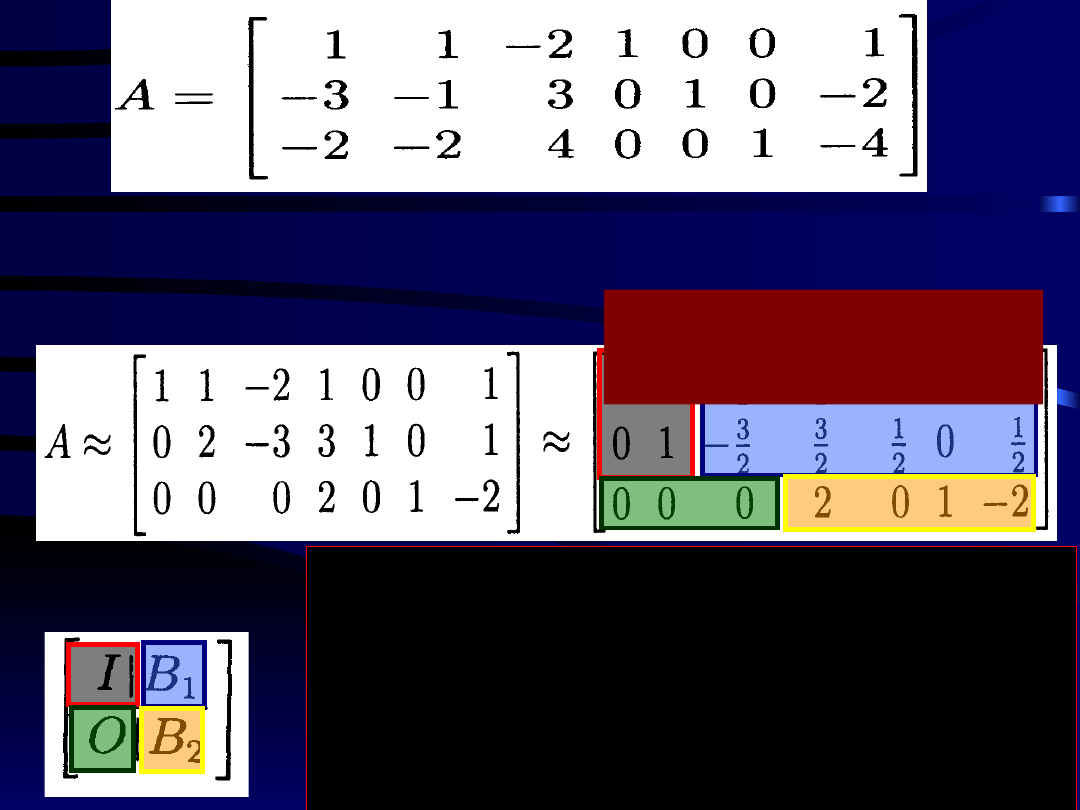
Przekształcając tę macierz poprzez

Przekształcając tę macierz poprzez

odpowiednie operacje elementarne,

odpowiednie operacje elementarne,

otrzymujemy kolejno

otrzymujemy kolejno

Jest to

Jest to

postać:

postać:

x

x

1

1

x

x

2

2

x

x

3

3

z

z

1

1

z

z

2

2

z

z

3

3

b

b

Zgodnie z Tw. 2 musimy

sprawdzić, czy układ równań o

macierzy uzupełnionej

B

2

=[2,0,1-2]

ma przynajmniej

jedno rozwiązanie bazowe

nieujemne

Układ:

2z

1

+ z

3

= -2

2z

1

+ z

3

= -2

Jeżeli za zmienną bazową przyjmiemy

Jeżeli za zmienną bazową przyjmiemy

z

z

1

1

(czyli

(czyli

z

z

3

3

powinna być równa 0) (oczywiście

powinna być równa 0) (oczywiście

jest tylko jedna zmienna bazowa!), to

jest tylko jedna zmienna bazowa!), to

otrzymamy następujące rozwiązanie bazowe:

otrzymamy następujące rozwiązanie bazowe:

z

1

= -1 , z

2

= 0 , z

3

=

0

Wniosek: nie jest to rozwiązanie

nieujemne

Jeżeli za zmienną bazową przyjmiemy

Jeżeli za zmienną bazową przyjmiemy

z

z

3

3

(czyli

(czyli

z

z

1

1

powinna być równa 0) to:

powinna być równa 0) to:

z

1

= 0 , z

2

= 0 , z

3

=

-2

Wniosek: nie jest to rozwiązanie

nieujemne

Układ nierówności nie ma

rozwiązania.

Układ nierówności nie ma

rozwiązania.

ALGORYTM

ALGORYTM

SIMPLEX

SIMPLEX

Krok 1:

Dodanie zmiennych bazowych

x

3

,

x

4

,

x

5

(ze znakiem plus gdyż nierówność
<)

2 x

1

+ 2 x

2

<

14

Warunek

W1

x

1

+ 2 x

2

< 8

Warunek

W2

4 x

1

< 16

Warunek

W3

2 x

1

+ 2 x

2

+

x

3

= 14

Z warunku

W1

x

1

+ 2 x

2

+

x

4

= 8

Z warunku

W2

4 x

1

+

x

5

= 16

Z warunku

W3

Krok 2:

Wyznaczenie zmiennych bazowych

x

3

,

x

4

,

x

5

2 x

1

+ 2 x

2

+

x

3

= 14

x

3

= 14 - 2 x

1

- 2

x

2

x

1

+ 2 x

2

+

x

4

= 8

x

4

= 8 - x

1

-

2 x

2

4 x

1

+

x

5

= 16

x

5

= 16 - 4 x

1

Krok 3:

Utworzenie macierzy

A I

gdzie:

I

- macierzą jednostkową o

wymiarach m x m

(macierzą współczynników przy

zmiennych

występujących w pierwszej bazie)

A

- jest macierzą współczynników

warunków ograniczających:

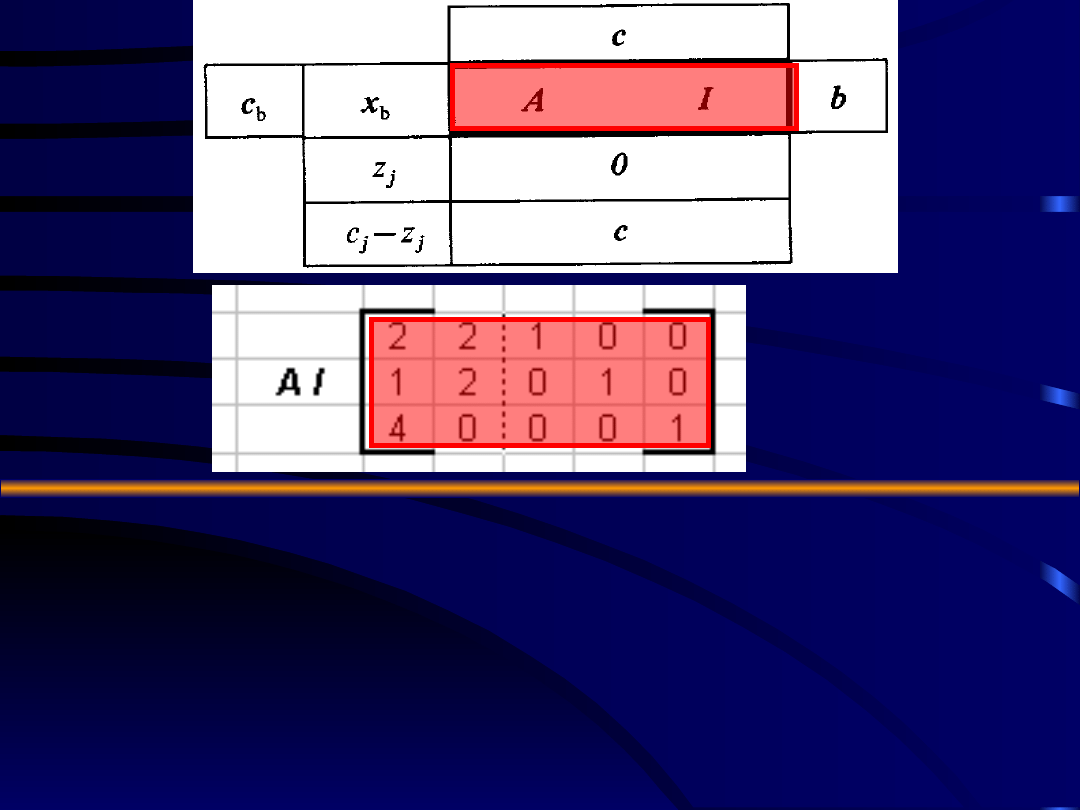
Tworzymy pierwszą macierz

bazową

czyli:



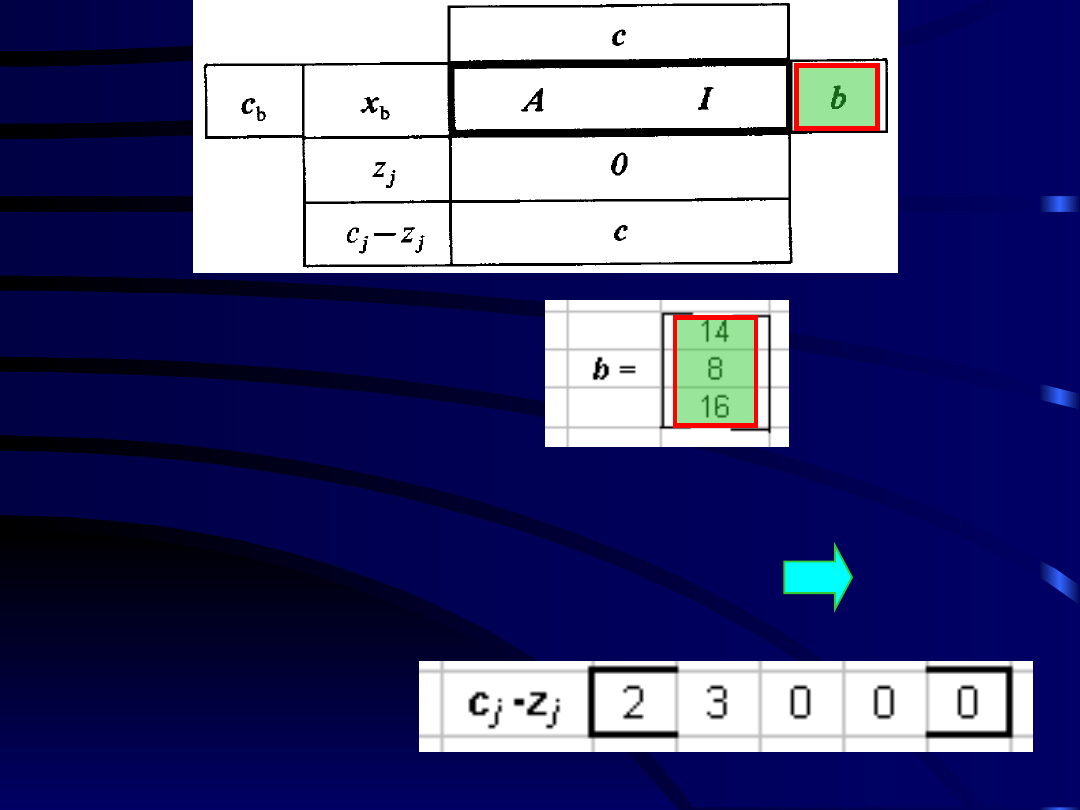
b - wektorem wyrazów wolnych

warunków ograniczających,

Zgodnie z równaniem f. celu

uwzględniającym zmienne bazowe mamy:

2 x

1

+ 3 x

2

+

0·x

3

+

0·x

4

+

0·x

5

max

A więc

c

j

– z

j

:

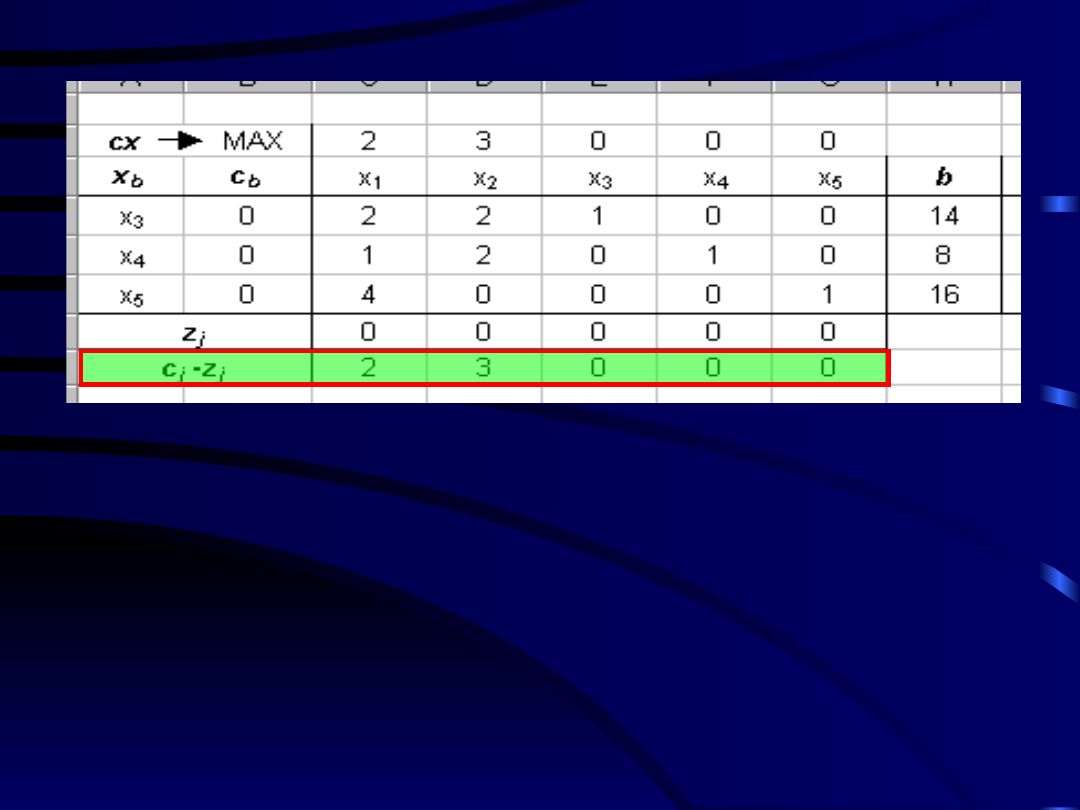
Odpowiadającą mu zmienną

x

j

wprowadzamy do

nowej bazy. Jeżeli największej wartości wskaźnika

optymalności odpowiada więcej niż jedna zmienna,

to do nowej bazy należy wprowadzić zmienną o

najmniejszym indeksie.

Krok 4: Pierwsza postać bazowa tablicy

simpleksowej:

Krok 5: Wybór zmiennej wprowadzonej do

bazy

Kierujemy się KRYTERIUM WEJŚCIA:

Wybieramy największą wartość wskaźnika

optymalności (

c

j

-z

j

).

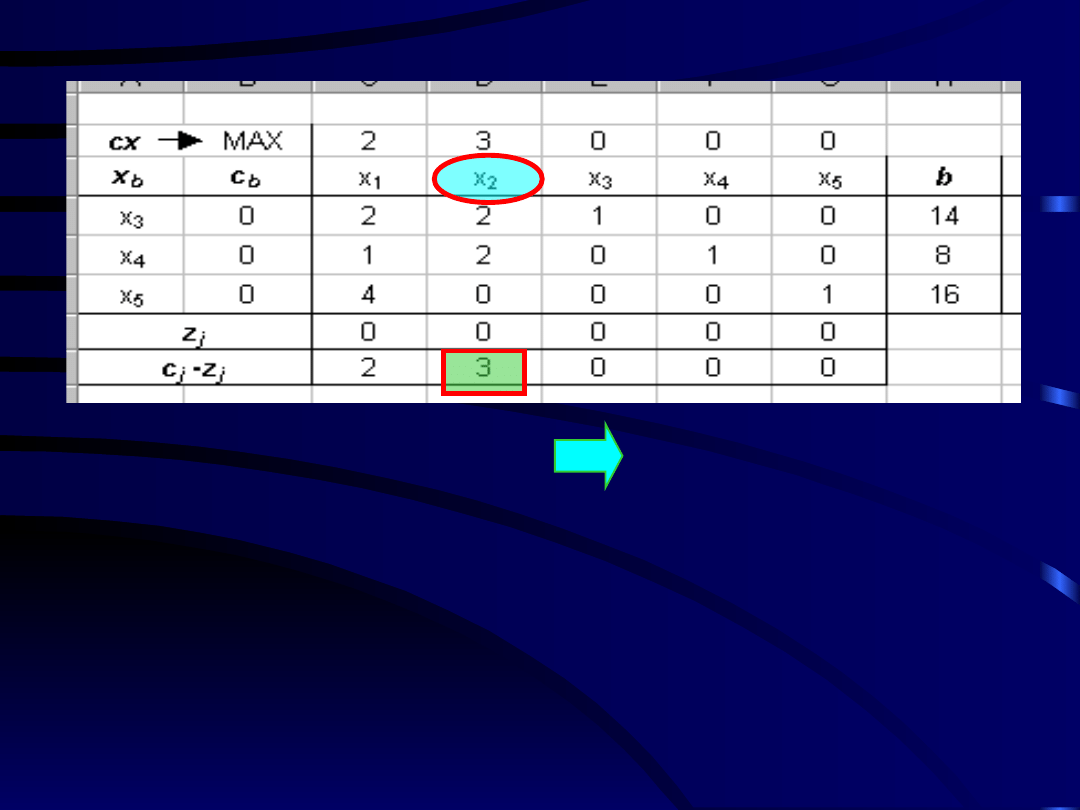
Ponieważ funkcja celu

max

,

wprowadzoną

zmienną do bazy będzie

x

2

(czyli

3

, bo to

jest największy współczynnik f. celu –

a

jednocześnie największy współczynnik

kryterium simpleks

c

j

-z

j

)

Krok 5 c.d.: Wybór zmiennej

wprowadzonej do bazy

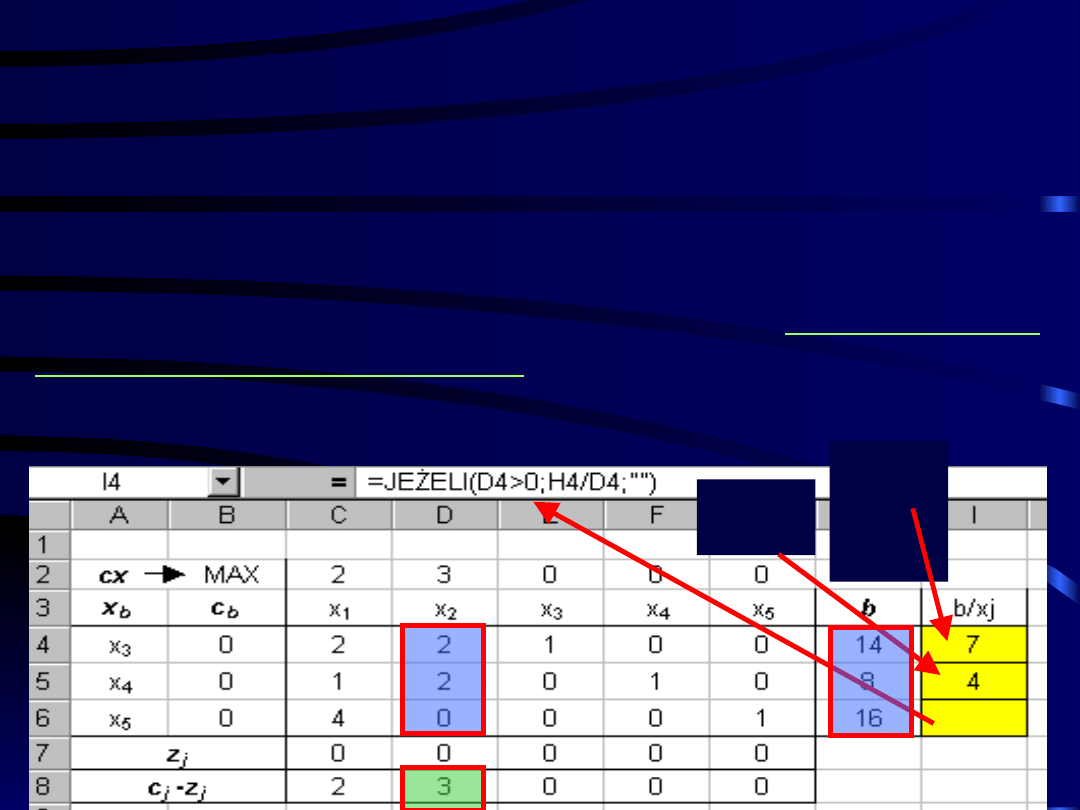
Zmienną wyprowadzamy z bazy zgodnie z

tzw. KRYTERIUM WYJŚCIA:

Krok 6: Wybór zmiennej opuszczającej

bazę

Bazę opuszcza ta zmienna, dla której

wyznaczony

iloraz jest najmniejszy

. Jeżeli wartość minimalna

jest przyjmowana więcej niż jeden raz, to jako

zmienną opuszczającą bazę należy wybrać zmienną o

najmniejszym indeksie.

14/
2

8/2

Obliczamy iloraz kolejnych wyrazów wolnych

(macierz b) przez odpowiadające im elementy

kolumny wchodzącej do bazy dla tych elementów

kolumny wprowadzonej do bazy, które są dodatnie.

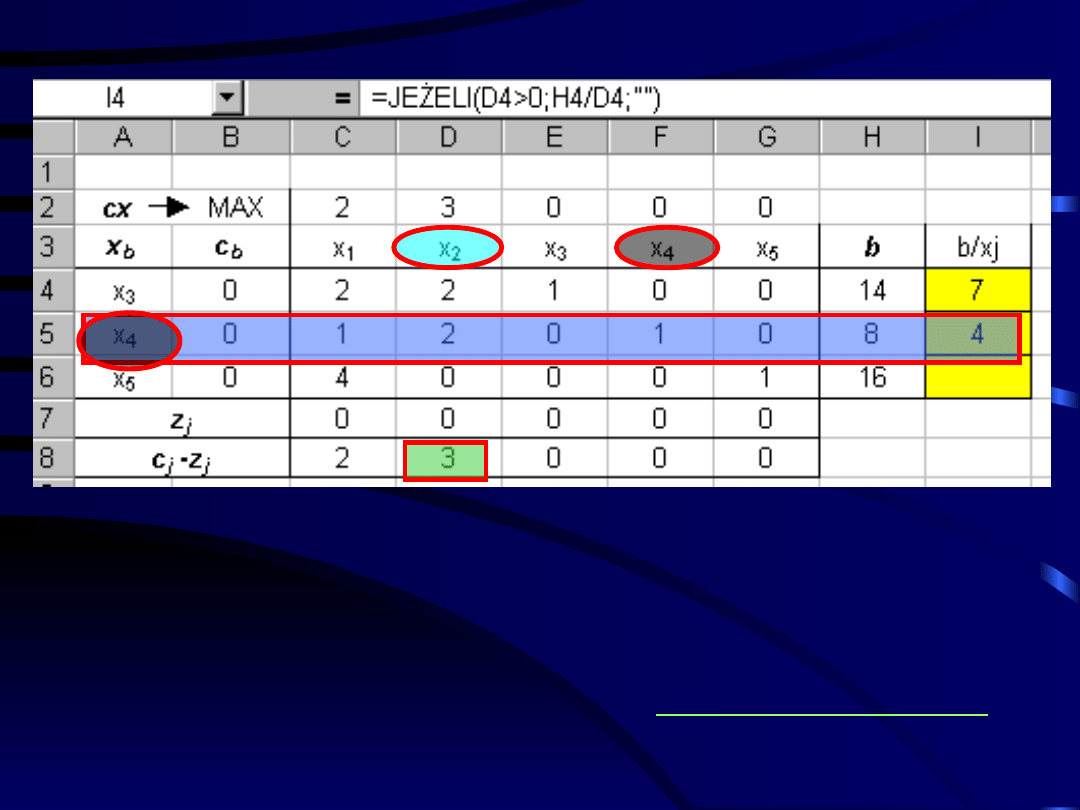
Krok 6 cd.: Wybór zmiennej opuszczającej

bazę

Ponieważ minimalny iloraz b/x

j

przyjmuje

wartość

4

dla zmiennej x

4

, dlatego

zmienną opuszczającą bazę jest zmienna

x

4

.

Podsumowanie:

zmienną wprowadzoną do

bazy była zmienna

x

2

, a zmienną

opuszczającą

bazę zmienna

x

4

.

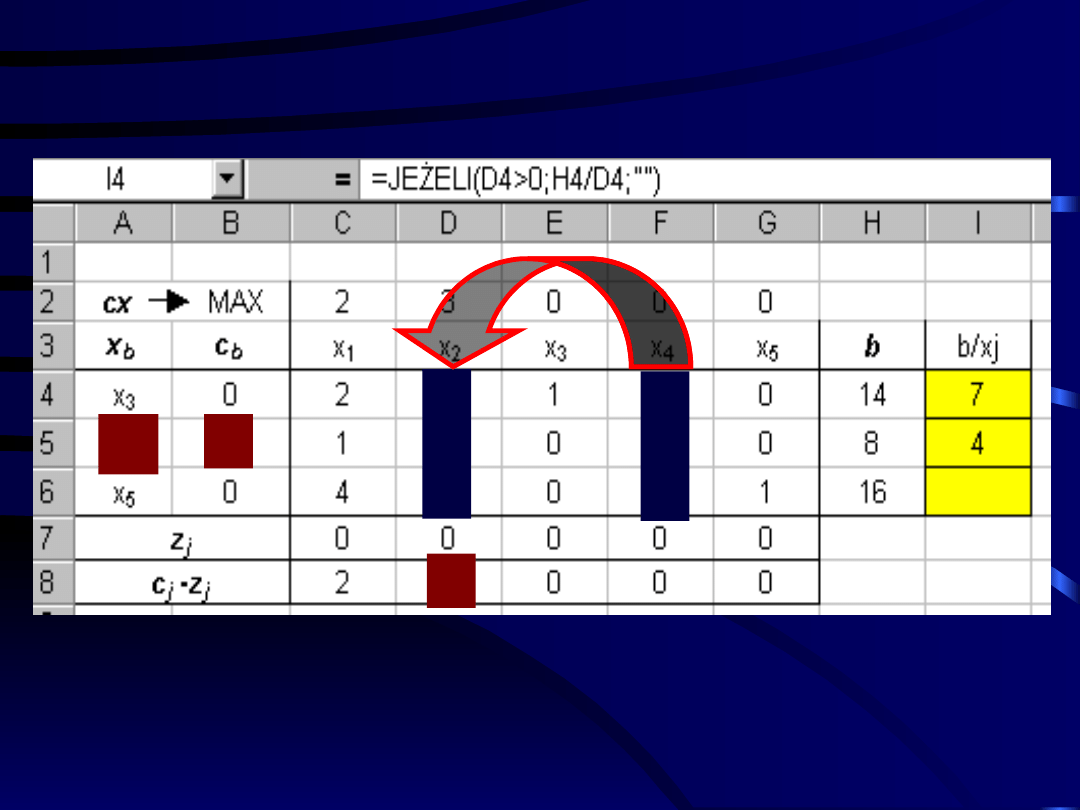
Krok 6 cd.: Wybór zmiennej opuszczającej

bazę

(tworzenie drugiej – sąsiedniej - macierzy

bazowej)

0
1
0

0
1
0

3

3

x

2

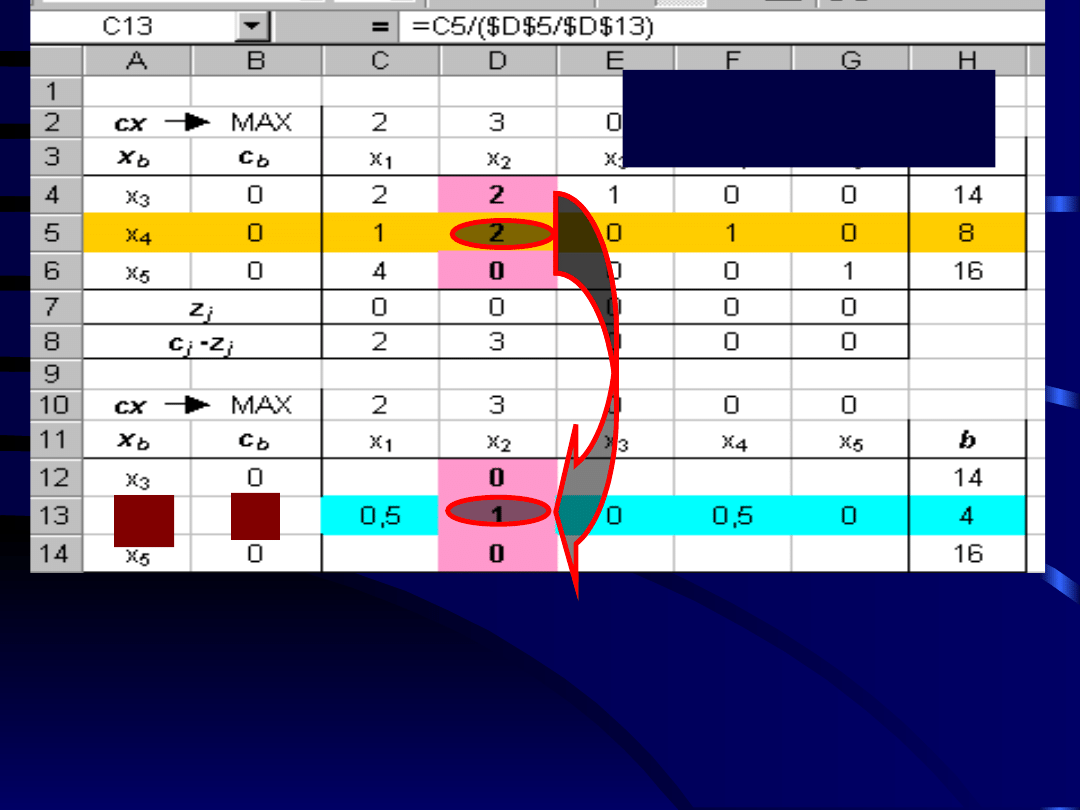
Ponieważ element a

22

macierzy A tworzącej

pierwszą postać bazową jest równy

2

, a element a

22

drugiej sąsiedniej postaci bazowej jest równy

1

,

więc aby otrzymać kombinację liniową drugiego

wiersza nowej macierzy, należy każdy element

drugiego wiersza pierwszej z macierzy podzielić

przez 2/1 = 2

Pierwsza postać
bazowa

3

x

2

Pierwsza postać
bazowa

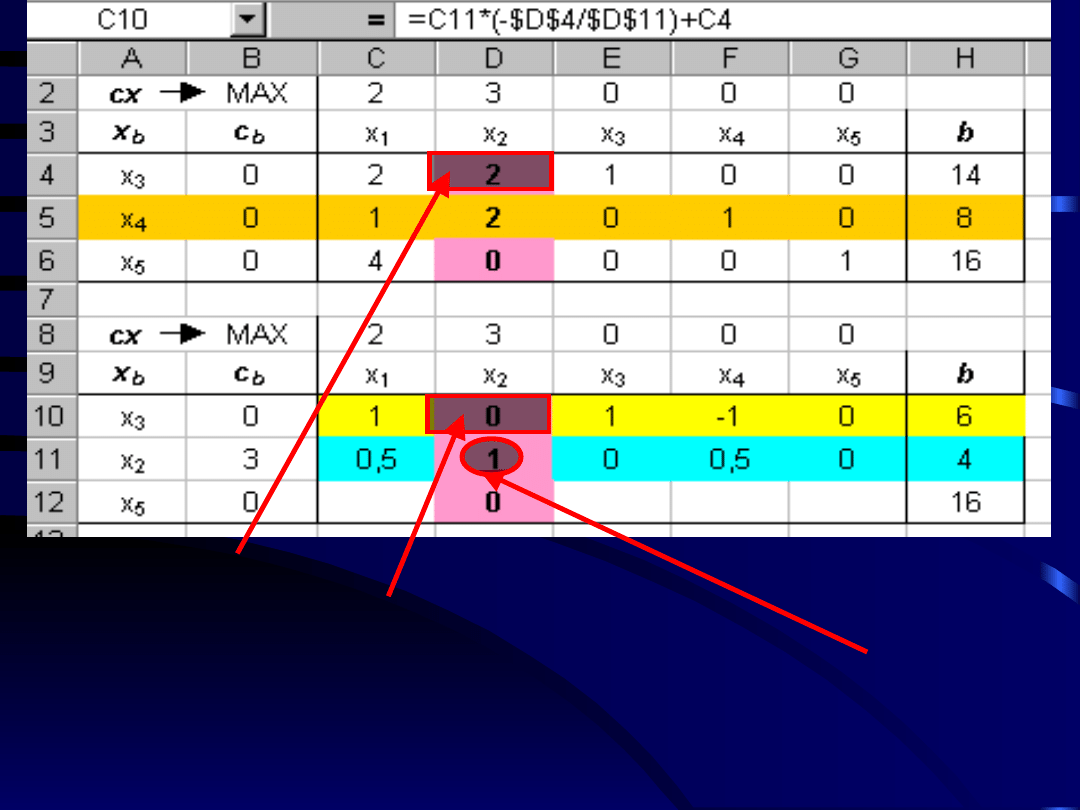
Element a

12

pierwszej postaci bazowej jest równy

2

, natomiast element a

12

drugiej postaci jest

równy

0

.

Pytanie:

przez jaką liczbę należy pomnożyć element

a

22

drugiej postaci bazowej aby po dodaniu jej do

elementu a

12

pierwszej postaci bazowej otrzymać

element a

12

drugiej postaci bazowej równy 0.

Odpowiedź: przez –2.

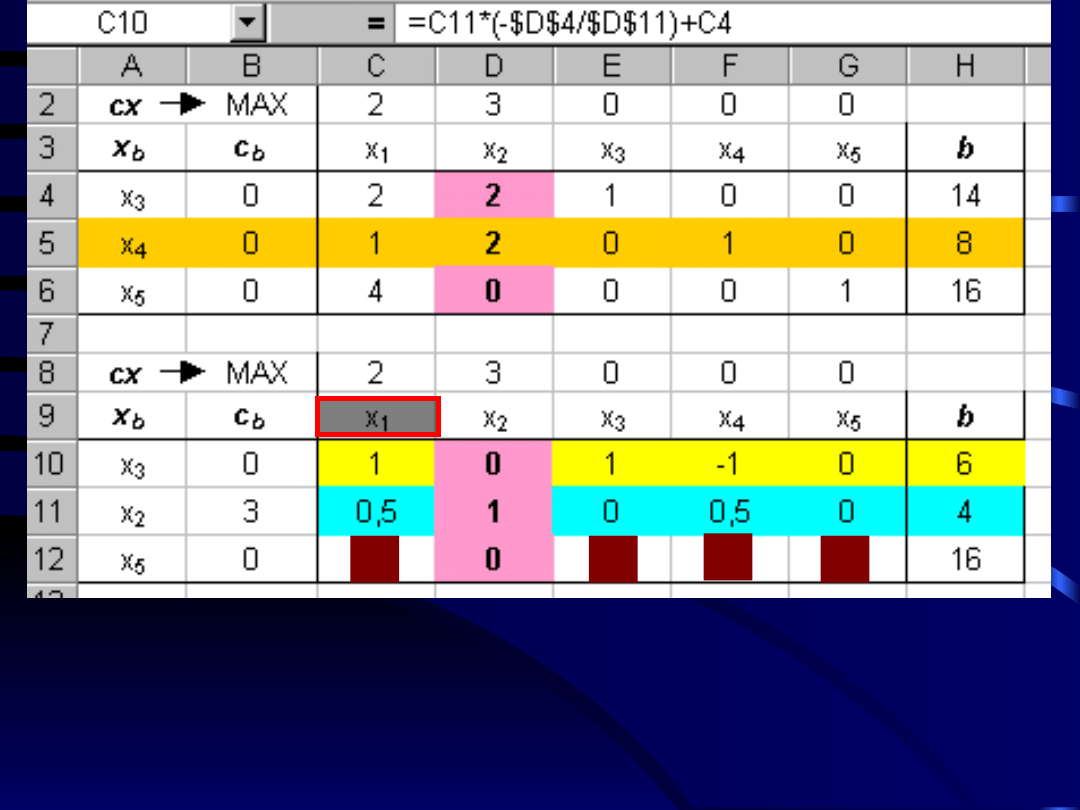
Element a

32

pierwszej postaci bazowej jest równy

0, natomiast element a

32

drugiej postaci jest

równy 0.

Ponieważ elementy są te same, więc trzeci wiersz

pierwszej postaci bazowej nie wymaga

przekształceń elementarnych.

4

0

0

1

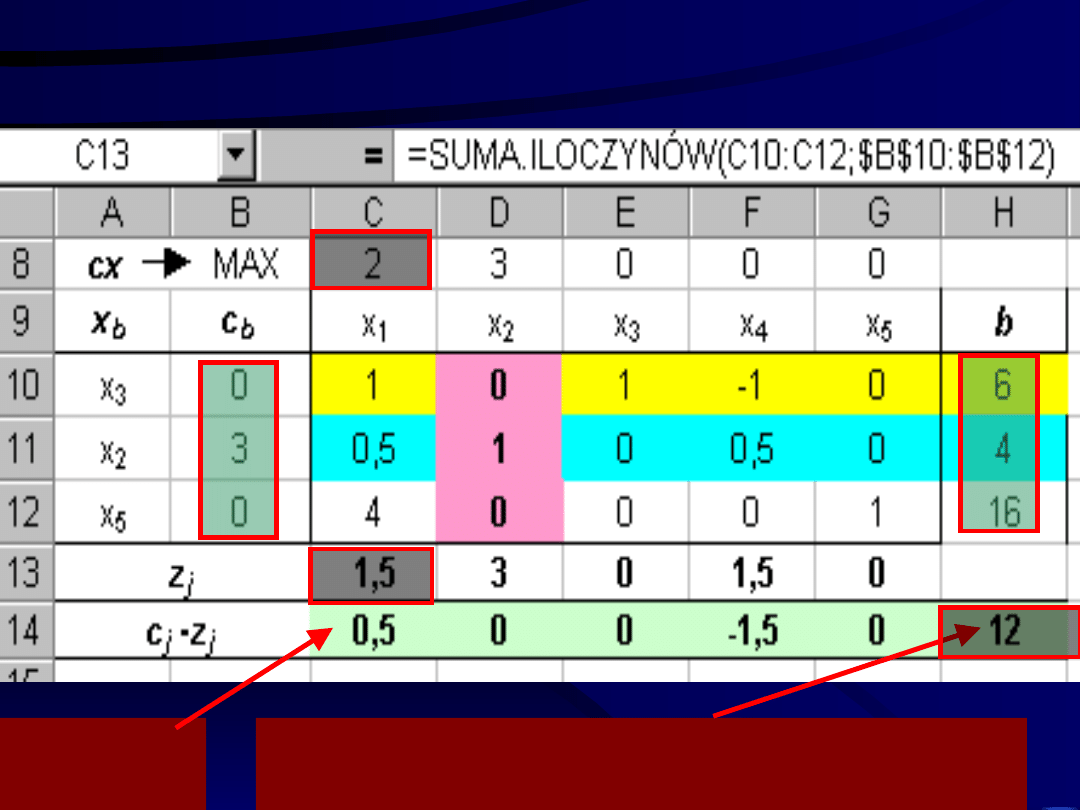
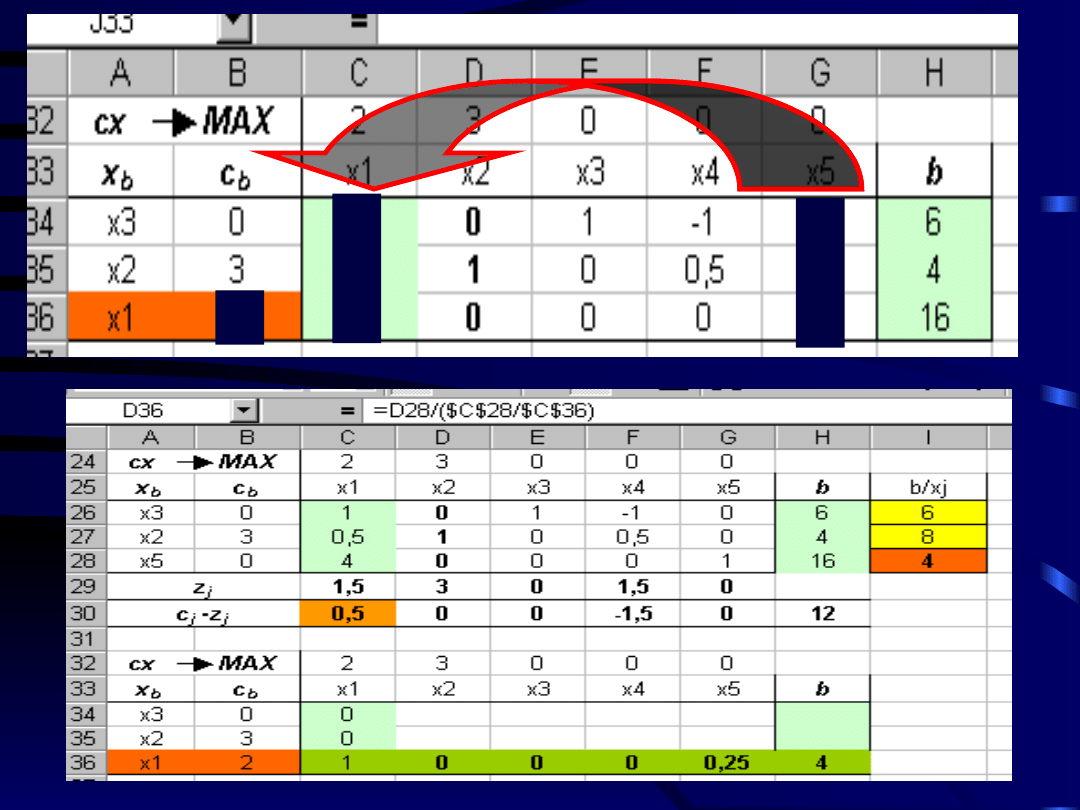
W kolejnym etapie obliczamy

wskaźnik optymalności c

j

– z

j

=C8-
C13

=SUMA.ILOCZYNÓW(H10:H12;$B$10:$
B$12)

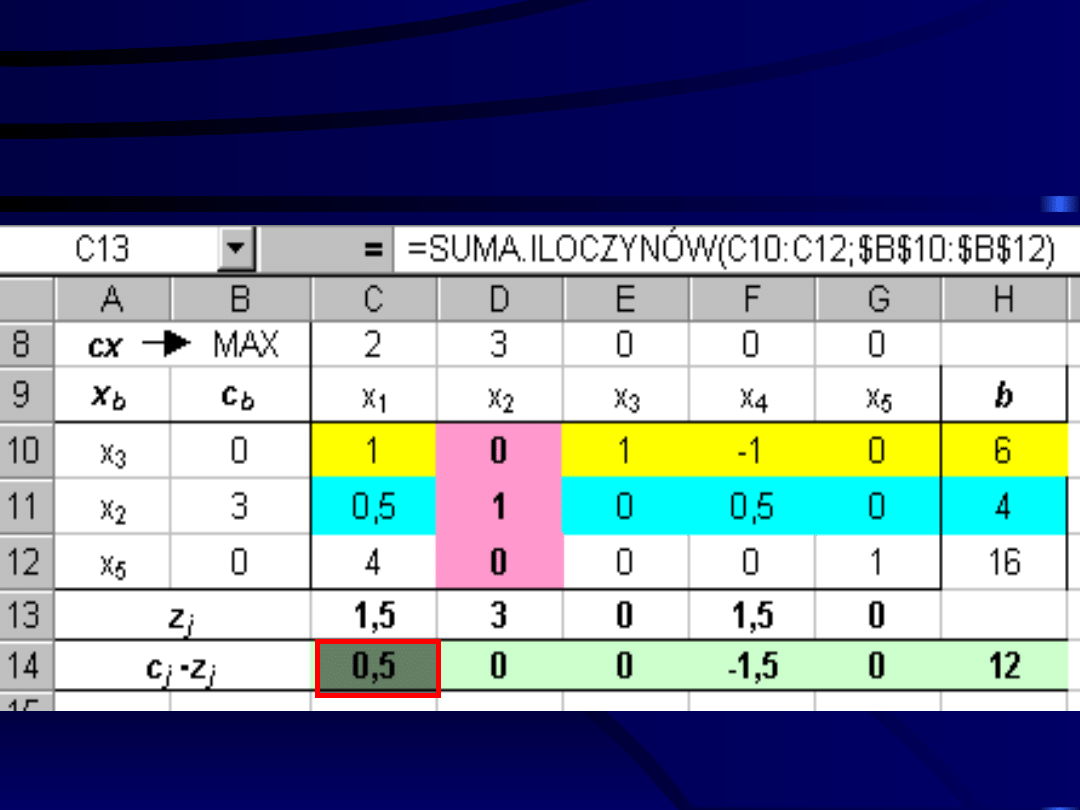
Ponieważ jeden ze wskaźników optymalności

c

j

– z

j

jest nieujemny (0,5) tak więc (zgodnie z

kryterium optymalności dla zadania

maksymalizacji) istnieje możliwość poprawy tego

rozwiązania.

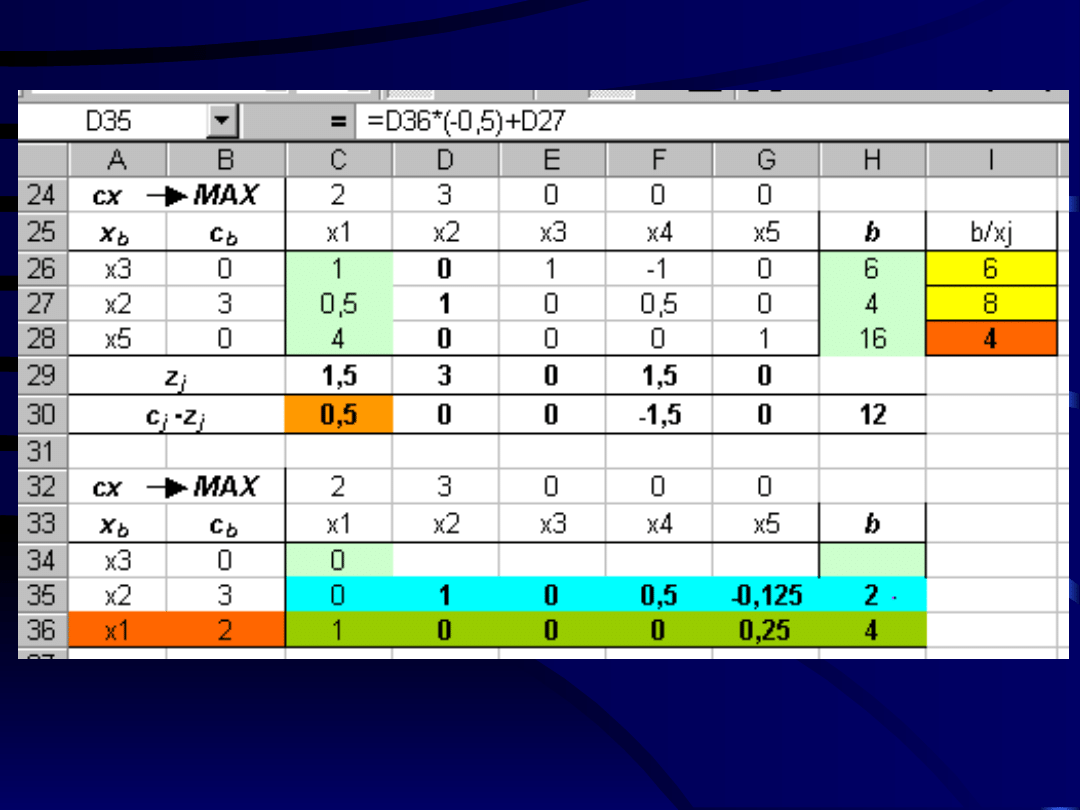
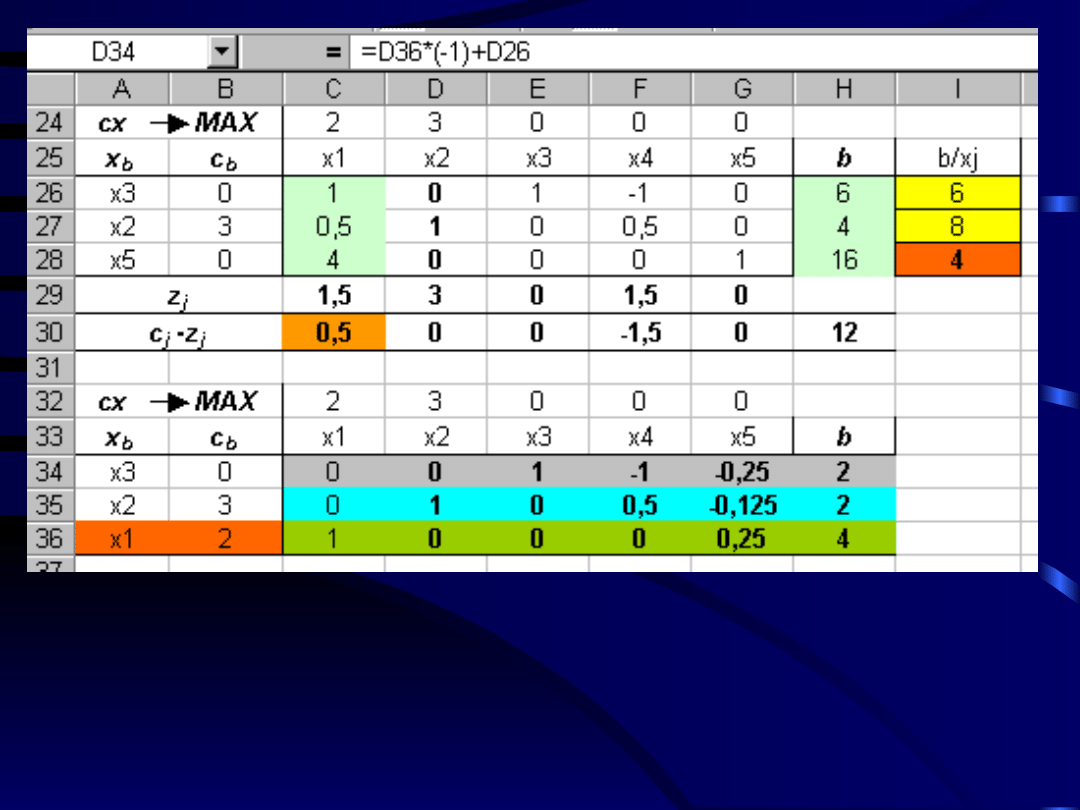
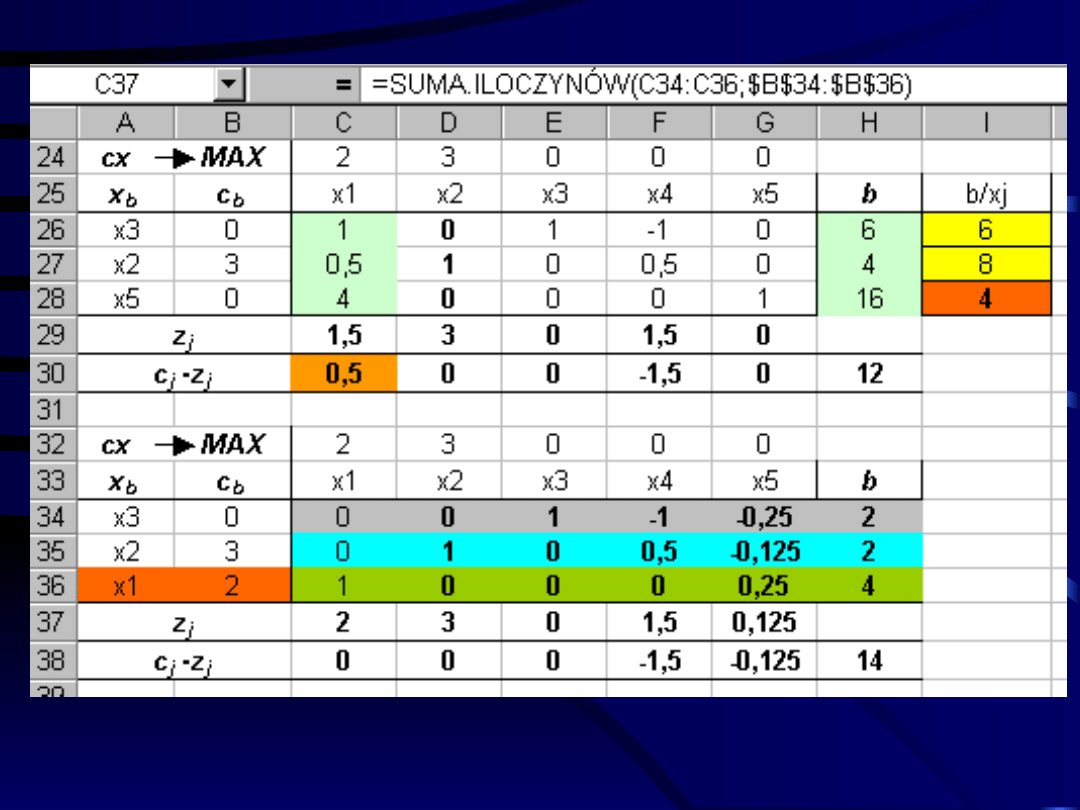
Budujemy kolejną tablicę simpleksową.

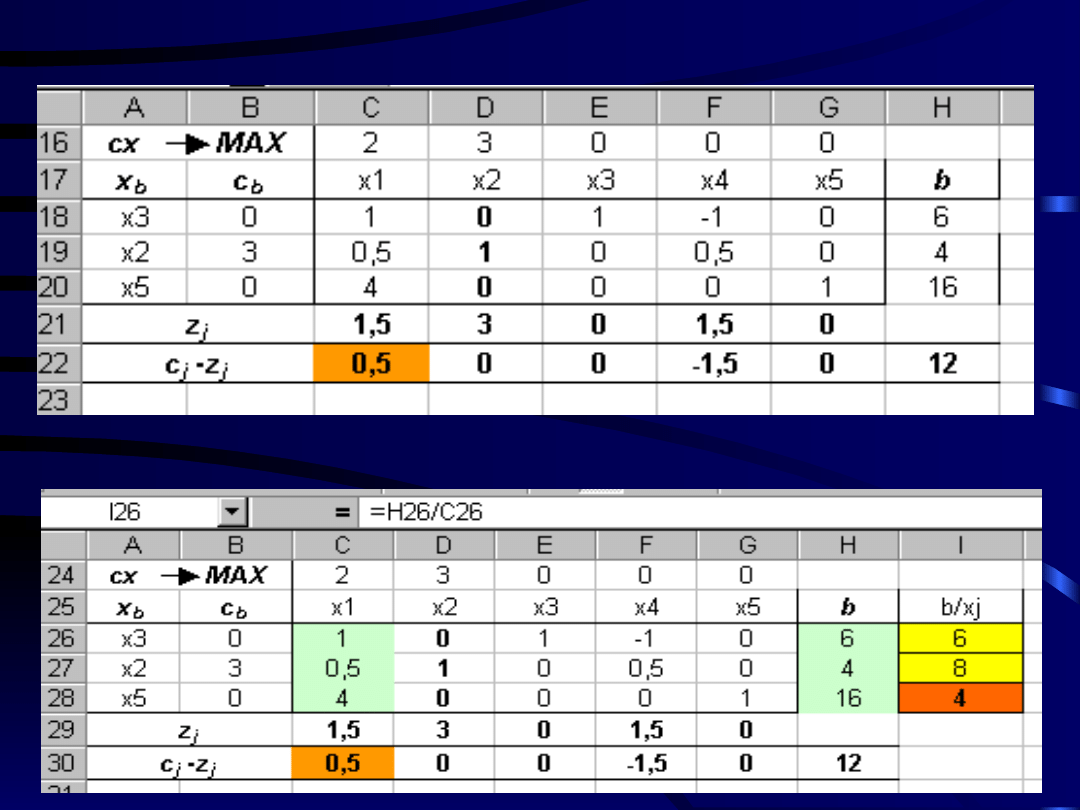
Zgodnie z kryterium wejścia do bazy wchodzi

zmienna x1.

Zgodnie z kryterium wyjścia bazę opuszcza

zmienna x5.

0
0
1

0
0
1

2